2. Choice of the Algorithm and Architecture of the Neural Network

[10]  The architecture of AAN was determined on the basis of the physical ideas on the cause-consequence relations and development of the global processes in the magnetosphere, the ionosphere being a part of the latter. According to that the input vectors in the architecture are subdivided to the vectors determining the prehistory (which describes the behavior of the complex of the critical frequency parameters) and vectors describing the near-Earth space.

[11]  As far as the search of the training sequence assumed a presence in the input database of the PSW and IMF parameters, exclusively for these parameters a separate input with the block of dynamical delay of the signal was created. This is due to the fact that the above indicated parameters are registered at a space vehicle far outside the Earth, i.e., earlier by a few hours than other parameters. To take into account the difference and to find what delay provides the best result, the block made it possible to regulate the delay time with a step of 30 min. From logical considerations this time should be within 1-3 hours. The second input has no delay. It is designed for the other parameters being registered directly on the Earth. As far as we assume to obtain as a result the only sequence (the temporal series of the forecasted values of the critical frequency) the output of the neural network is one neuron.

[12]  It is known that the algorithm of training neural networks is analogous to the algorithms of the search for the extreme of a function of many dimensional variables. In the ANN of error backpropagation, to do that the error appearing in the entrance layer is calculated and the vector of the gradient as a function of the weights and shifts is calculated. This vector indicates the direction of the shortest descent along the plane to the given points, so if one moves in this direction the error decreases.

[13]  The descent algorithm used earlier [Barkhatov et al., 2000] uses a constant step of iteration and is quite inefficient in the case when the derivatives with the respect to various weights differ considerably and the function relief is very complicated. In this case for a smooth decrease of the error one should choose very small training rate dictated by the maximum derivative, whereas the distance to the minimum by an order of magnitude is determined by the maximum derivative. As a result the teaching process becomes very slow. Moreover oscillations inevitably occur in the vicinity of the minimum and the teaching looses its attractive quality of the error decrease. Among the algorithms performing the above indicated operation and using the method of error backpropagation, there are more sophisticated algorithms free of this defect. First of all, it is an algorithm of conjugated gradients based on the permanent correction of the iteration step and a search for an optimum descent down to the minimum. Even more sophisticated and alternate to the previous one is the Levenberg-Marquardt (LM) algorithm [Medvedev and Potemkin, 2002] based on calculations of the second partial derivatives with respect to weights and shifts from the error functional. This algorithm enters the group of the quasi-Newton methods.

Figure 1

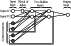
[14]  The preliminary numerical simulations confirmed correctness of the theoretical reason of the choice of the proper architecture of the neural network and algorithm. As a result, a two-layer network was considered. Each hidden layer of this network contains two neurons having feedback loops. It is realized by an intrusion into the scheme of context neurons. This separation of the input vectors (parameters) caused by the physical reason and their considerable quantity satisfy the chosen LM algorithm. This algorithm requires enough branching of the network and multistep internal nonlinear memory. This can be provided in our case only be an increase of the hidden layers. The architecture of the used network is shown in Figure 1.

[15]  The Newton method is used for the accelerated training of the chosen ANN. The main step of the method is determined by the relation

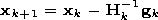(1)

where x_k is the vector of the tuned parameters, H_k is the Gesse matrix of the second partial derivatives of the error functional on the tuned parameters, and g_k is the vector of the gradient of the error functional. The minimization procedures based on the Newton method as a rule convergence more rapidly than the same procedures based on the method of conjugated gradients. However, the calculation of the Gesse matrix is a complicated and expensive (in the computation aspect) procedure. Therefore a set of algorithms was developed on the basis of the Newton method but not requiring calculation of the second derivatives. This set of quasi-Newton algorithms uses at each iteration some approximated evaluation of the Gesse matrix.

[16]  The Levenberg-Marquardt algorithm (trainlm in the terminology of the MATLAB system) realizes the following strategy for evaluation of the Gesse matrix. Assuming that the functional is determined as a sum of errors squared, the Gessian may be approximately calculated as

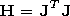(2)

and the gradient calculated by

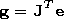(3)

where J = dJ/d W is the Jacoby matrix of the derivatives of the error functional on the tuned parameters and e is the vector of the network errors. The Jacoby matrix can be calculated using the standard method of the return propagation of the error, the method being much simpler than calculation of the Gesse matrix.

[17]  The trainlm algorithm uses the above indicated (2) approximation of the Gessian:

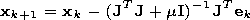(4)

where I is the unit matrix. When the m coefficient is equal to zero, we obtain the Newton method in the form of (2); when the value of m is high we obtain the gradient descent method with a small step. As far as the Newton method has a high accuracy and convergence rate in the vicinity of the minimum, the problem is in the minimization process to transfer as soon as possible to the Newton method. To do that, the m parameter is decreased after each successful iteration and is increased only then when the test step shows that the error functional increases. This strategy provides a decrease of the error after each iteration of the algorithm.

[18]  The algorithms based on the approximated Newton method require a larger amount of calculations at each iteration and vaster memory volume. Using these algorithms one has to keep at each iteration the estimate of the Gesse matrix, its dimensions being determined by the number of the tuned parameters. One can hardly able to determine which training algorithm would be the most rapid while solving this or that problem. It depends on many factors including the completeness of the problem, number of elements of the training arrays, number of tuned parameters of the network, and the final error. For the networks whose matrixes of weights and shifts have hundreds of elements (their number in their turn is determined by the dimensions of the input vectors) the LM algorithm has the most rapid convergence. This advantage is especially important if a high accuracy of the training is required.

[19]  The main defect of the LM algorithm is that it requires a considerable volume of the operative memory to keep large matrixes. The latter means that to evaluate matrix (2) one would need considerable resources for its calculation and storage. As the MATLAB system is oriented to the work with matrices, it presents all versions of their processing and presentation, including a decomposition of large matrices. The work of the LM training algorithm may be programmed in such a way that the matrix of the Gessian evaluation can be split to several submatrices. Let two submatrices are available. Then (2) can be written in the form

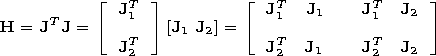(5)

Thus the estimate of the Gessian may be calculated using the submatrices of smaller sizes. In the process of Gesse matrix formation the used submatrices may be withdrawn from the operative memory. Such strategy makes it possible to save the volume of the operative memory but decreases the operation rate (was not used in this work). Often it is not enough for a stable numerical computation, because complicated computer algorithms of the MATLAB 6 system are sensitive to the total resources of the computer. Any new switching of the AAN training by the LM algorithm each time shows different accuracy of the tuning including the most unsatisfactory. It may be due to the residual filling in/overfilling of the operative memory, and overloading of the computer by background programs.