2. Solar Cycle in the Solar and Heliospheric Characteristics

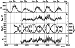
Figure 1

[5]  In Figure 1 the time history of the relative Zurich sunspot number ( R_Z, panel a) is compared for 1950-2003 with those of some heliospheric parameters. The strength of the interplanetary magnetic field B _IMF near the Earth is depicted in panel b. Panel c shows the GCR intensity (the count rate of the omnidirectional Geiger counter in the maximum of the transition curve in the stratosphere at Murmansk, the thin line in counterphase with the sunspot number, right y axis) and its modulation with respect to 1965 solar minimum, M _Mu= (N _Mu¹⁹⁶⁵ - N _Mu) / N _Mu¹⁹⁶⁵ 100% , where N _Mu¹⁹⁶⁵ is the count rate for May 1965 (the thicker line in phase with the sunspot cycle, left y axis). The magnetospheric Kp index is shown in Figure 1d. (The 27-day or monthly average data (except N _Mu ) are taken from http://nssdc.gsfc.nasa.gov/omniweb/ow.html.) The thin vertical dotted lines show the maxima labelled with M (and the solar cycle number as a subscript) and minima ( m ) in the 13-month smoothed sunspot number.

[6]  As one can see from Figure 1, the solar cycle in the GCR intensity modulation is the most pronounced and smooth when compared with other heliospheric indices shown. Besides the solar cycle in the GCR intensity modulation reminds that in the sunspot number in the most degree. The probable cause of these facts is that the GCR intensity, even measured at one point in the heliosphere, is in fact the global heliospheric index, as the GCRs effectively "average" relevant heliospheric characteristics along their way to the point of measurement.

[7]  We also use Figure 1c to illustrate what GCR characteristics and effects we keep in mind when we are seeking to isolate the solar cycle extreme phases in the GCR intensity modulation. One can see that at some time ( t= t_m ^GCR ) about a few months after the SC minimum the GCR intensity peaks at its local maximum, while at some time ( t= t_M ^GCR ) after the maximum in R_Z the GCR intensity reaches its local minimum. If one knows the GCR intensity J_m, corresponding to the minimum of solar activity (and better still, its dependence on the particle energy, position in the heliosphere etc.), it is possible to study the so-called residual GCR intensity modulation, J_IS J_m, of the interstellar intensity JIS to that corresponding to the most quiet Sun, J_m. As the J_m changes when one moves to the past solar cycles (it can be done with the GCR radioactive tracers [McCracken and McDonald, 2001]), the long-term or secular variation of the heliospheric and solar activity can be studied. Similarly, knowing also the GCR intensity J_M, corresponding to the maximum of solar activity, the 11-year GCR intensity modulation can be studied, J_m > J_M. Besides one can see that both the value of J_m and the form of the intensity time profile around it are different for the successive solar cycles, which is due to opposite polarity distribution of the large-scale interplanetary magnetic field, which in turn is the manifestation of the 22-year, or magnetic, solar cycle. Around solar activity minima this polarity is usually described by the quantity A=+1 or A=-1, which sign coincides with that of the radial component of the high-latitude magnetic field in the northern photosphere. So the 22-year variation in the GCR intensity, J_m,+ J_m,-, can be studied (the second subscript stands for the sign of A ).

[8]  However, it is clear that to determine in proper way the above extreme values ( J_m,+, J_m,-, and J_M ) one should consider the GCR behavior in some time intervals t_m¹ < t < t_m² and t_M¹ < t < t_M² around t_m ^GCR and t_M ^GCR, respectively, when this behavior and the physical processes forming it have some features common to the interval in question and distinguishing it from the preceding and following solar cycle phases. We call these intervals the minimum and maximum or extreme phases of the solar cycle. As one can see from Figure 1c beside being useful in defining the extreme GCR intensity values, the minimum SC phase is characterized by the processes forming the intensity time profiles different for the successive solar cycles while the maximum solar cycle phase is characterized by the double-peak structure (or Gnevyshev Gap effect [see Krainev et al., 1999]) in the GCR intensity modulation.