INTERNATIONAL JOURNAL OF GEOMAGNETISM AND AERONOMY VOL. 5, GI1005, doi:10.1029/2003GI000053, 2004
6. Conclusions
[28] Concluding, we emphasize once more that the estimation of the
accuracy of numerical simulation of the
N distribution in LREI is a
rather complicated problem. It may seem that the simplest way to
determine the error
D N is a comparison of the
N simulation results
to its values measured by rockets. However, the errors in
measurements of local values of
N during the first tens of seconds
after an explosion may reach unacceptably large values (up to an
order of magnitude) due to the increase in the radiation level (if
probe methods of measurements are used) and the medium
nonstationarity along the radio wave propagation path (if the
dispersion interferometer is used).
[29] In these conditions a special attention should be drawn to the
measurement methods based on radiolocation of the ionospheric
plasma and analysis of the parameters of radio wave propagating in
the ionosphere
[see, e.g., Al'pert, 1972;
Galkin et al., 1971].
It is
worth noting that many very popular methods (the methods of pulse
radiosounding, partial reflection, incoherent scatter and others) are
not acceptable for studying LREI at
t 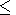 100 s after the explosion due
to the high level of the radio wave absorption. In the short-wave
range (used for radiophysical measurements of the medium
parameters) at the first seconds after the explosion according to
equation (1) the condition
e'
100 s after the explosion due
to the high level of the radio wave absorption. In the short-wave
range (used for radiophysical measurements of the medium
parameters) at the first seconds after the explosion according to
equation (1) the condition
e' 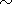 e'' is fulfilled in LREI. In this case it is
impossible to find if the exponential depletion of the field is due to
the absorption or to the exit into the caustic shadow. Irregularity of
the absorption in such medium initiates the emission diffusion into
the regions with the stronger absorption
[Kravtsov, 1967].
One
can show that the trajectory of the electromagnetic energy of the
SW range waves in LREI is influenced by the distribution in it of not
only real but imaginary part of the plasma permeability as well.
e'' is fulfilled in LREI. In this case it is
impossible to find if the exponential depletion of the field is due to
the absorption or to the exit into the caustic shadow. Irregularity of
the absorption in such medium initiates the emission diffusion into
the regions with the stronger absorption
[Kravtsov, 1967].
One
can show that the trajectory of the electromagnetic energy of the
SW range waves in LREI is influenced by the distribution in it of not
only real but imaginary part of the plasma permeability as well.
[30] It follows from the performed studies that the conditions of radio
wave propagation though LREI are mainly determined by the
attenuation. Therefore evaluating the accuracy of the
N numerical
simulation in the lower ionosphere one should concentrate attention
on methods of absorption measurements. Such methods are
[Galkin et al., 1971]
the method of the vertical sounding of the
ionosphere
(A1), method of registration of the extraterrestrial
sources (A2), method of registration of the field strength of the
signal from a remote radio station operating in permanent regime
(A3), and others. We note that the A1 method is not acceptable for
measurements of the radio wave attenuation in LREI because of a
high level of the attenuation and the most suitable and often used is
the A2 method (see, for example, the review by
Belikovich and Benediktov [1969]).
[31] The remote measurements of the
N(h) vertical profile within LREI
on the basis of the absorption
d w measured by the A2 method
are based on the solution relative to
N(h) of integral equation (25).
Belikovich et al. [1964]
reduced equation (25) to the Fredholm
equation of the first type with the residual kernel and obtained a
general formula for calculation of
N(h) from the
d (w) curve. It
follows from this solution that to find
N at some height
hi, it is
enough to know
n eff,
dn eff/dh and the attenuation function
d (w) with
its frequency derivatives
w = n eff(hi).
To obtain the
N(h) profile within
the height interval
h=40-80 km one has to have measurements of
these values in the frequency range from a few megahertz to
hundreds of megahertz. Unfortunately, there are no experimental
values of the radio wave absorption in the needed amount and with
acceptable accuracy
[Belikovich and Benediktov, 1973;
Zhulin, 1964].
[32] At the same time, the available measurements of attenuation at
various frequencies make it possible not only to estimate the errors
of the simulation results of the absorption in LREI but to check the
errors in simulation of
N. Actually, the errors in measurements of
radio wave attenuation
D d/ d are of a few percent
[see, e.g., Belikovich and Benediktov, 1973, Figure 1],
so we principally are
able to control the errors in the attenuation calculations with very
high accuracy. Using the algorithm developed above (the
methodical error of which does not exceed a few percent), we may
the entire discrepancy between the calculated and measured values
of the attenuation explain by the error in
N simulation in the
conditions of SNE. At the same time, asymptotic estimates (27)
show that at correct enough approximation of the values of
n eff(h) (see curve 2 in Figure 4) the relative error
D N/N 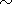 D d/ d . Thus the
method of attenuation measurements used during the experimental
SNE makes it possible to check the error in simulation of
N with
the accuracy of a few percent. However, as far as the radio wave
absorption within LREI is determined by integral (25), to provide
such error in simulation of the
N(h) profile one needs the
corresponding accuracy of agreement between the simulation
results and the measured values of attenuation within the entire
frequency range (from a few megahertz to a thousand and more
megahertz). For the frequencies from a few megahertz to hundreds
of megahertz one has to take into account fairly correctly the level
of the synchrotron radioemission of the high-energy electrons of the
artificial radiation belt formed during SNE
[Peterson, 1967;
Zhulin, 1964].
D d/ d . Thus the
method of attenuation measurements used during the experimental
SNE makes it possible to check the error in simulation of
N with
the accuracy of a few percent. However, as far as the radio wave
absorption within LREI is determined by integral (25), to provide
such error in simulation of the
N(h) profile one needs the
corresponding accuracy of agreement between the simulation
results and the measured values of attenuation within the entire
frequency range (from a few megahertz to a thousand and more
megahertz). For the frequencies from a few megahertz to hundreds
of megahertz one has to take into account fairly correctly the level
of the synchrotron radioemission of the high-energy electrons of the
artificial radiation belt formed during SNE
[Peterson, 1967;
Zhulin, 1964].
[33] It has been mentioned above that the results of the numerical
simulation of
N in the frequency range from 100 to 1000 MHz
[Kozlov, 1967, 1971;
Kozlov and Kudimov, 1969;
Kozlov and Raizer, 1966]
have an error of tens of percent. For the lower
boundary of this range the calculated values of the attenuation by
50-90% exceed the experimental values. For the upper boundary
the simulation results are by about the same value lower than the
experimental data. Therefore the
N(h,t) profile from
Kozlov [1967, 1971],
Kozlov and Kudimov [1969],
and
Kozlov and Raizer [1966]
strictly speaking is not able to explain the frequency
dependence of
d (w) in the frequency range from a few megahertz
to 1000 MHz obtained experimentally.
[34] For the sake of objectivity, one has to note that during the recent
years a series of papers has appeared
[Kozlov, 1987a,
1987b;
Kozlov et al., 1982, 1988, 1990;
Smirnova et al., 1984;
Vlaskov et al., 1983].
These papers in our opinion make it
possible to improve considerably the method of numerical
simulation of the spatial-time distribution of
N in LREI of SNE and
achieve an agreement between the simulation results and
experimental data in the entire frequency range. The decrease of the
considered interval down to a few megahertz provides a need to
study the electron-ion balance kinetics of the ionosphere disturbed
by the explosion up to
F region heights
[see, e.g.,
Dyadichev and Kozlov, 1976].
Development of a specified mode on the basis of
these publications requires more attentive choice of the reaction
rate constants currently determined within a rather broad interval,
specification of the initial data on the explosives, atmospheric state
etc. Specifying this model in the regions located at the periphery of
the direct visibility from the explosion point, one should consider in
more detail the problem of propagation of penetrating radiation in
the inhomogeneous atmosphere
[Lobolev, 1997a,
1997b;
Kukhtevich and Mashkovich, 1979])
and
provide taking into account the voluminous character of this
radiation source and its motion in space.

Citation: Semenov, B. I., V. V. Treckin, and S. I. Kozlov (2004), Influence of the lower region of the enhanced ionization produced by a space nuclear explosion on radio wave propagation, Int. J. Geomagn. Aeron., 5, GI1005, doi:10.1029/2003GI000053.
Copyright 2004 by the American Geophysical Union
Powered by TeXWeb (Win32, v.1.5).
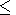 100 s after the explosion due
to the high level of the radio wave absorption. In the short-wave
range (used for radiophysical measurements of the medium
parameters) at the first seconds after the explosion according to
equation (1) the condition
e'
100 s after the explosion due
to the high level of the radio wave absorption. In the short-wave
range (used for radiophysical measurements of the medium
parameters) at the first seconds after the explosion according to
equation (1) the condition
e' 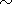 e'' is fulfilled in LREI. In this case it is
impossible to find if the exponential depletion of the field is due to
the absorption or to the exit into the caustic shadow. Irregularity of
the absorption in such medium initiates the emission diffusion into
the regions with the stronger absorption
[Kravtsov, 1967].
One
can show that the trajectory of the electromagnetic energy of the
SW range waves in LREI is influenced by the distribution in it of not
only real but imaginary part of the plasma permeability as well.
e'' is fulfilled in LREI. In this case it is
impossible to find if the exponential depletion of the field is due to
the absorption or to the exit into the caustic shadow. Irregularity of
the absorption in such medium initiates the emission diffusion into
the regions with the stronger absorption
[Kravtsov, 1967].
One
can show that the trajectory of the electromagnetic energy of the
SW range waves in LREI is influenced by the distribution in it of not
only real but imaginary part of the plasma permeability as well.
