INTERNATIONAL JOURNAL OF GEOMAGNETISM AND AERONOMY VOL. 5, GI1005, doi:10.1029/2003GI000053, 2004
4. LREI Model
[19] In the LREI model (11) the spatial coordinates are
h and the
distance to the epicenter axis
l (see Figure 1). To obtain the explicit
solution of equations (3) and (4) by the method of variable
separation
[Semenov, 1974]
in the analytical model (11), one is
able only in the case of remote from the epicenter vertical sounding
of LREI, or in the cases
( JMb, JMN  D H2/ 4b0 ), when one can
neglect the horizontal gradients. The latter situation takes place
during SNE of relatively small equivalents occurring at considerable
distances from the Earth when the LREI influence on the radio
wave propagation is insignificant. We here are interested in cases of
the strongest impact of LREI on the operation of radio systems
when one cannot separate the variables in equations (3) and (4) for
model (11). However, one can easily see
(see, e.g., Table 1 and
equations (2) and (11)) that under
t
D H2/ 4b0 ), when one can
neglect the horizontal gradients. The latter situation takes place
during SNE of relatively small equivalents occurring at considerable
distances from the Earth when the LREI influence on the radio
wave propagation is insignificant. We here are interested in cases of
the strongest impact of LREI on the operation of radio systems
when one cannot separate the variables in equations (3) and (4) for
model (11). However, one can easily see
(see, e.g., Table 1 and
equations (2) and (11)) that under
t  1 s and
w
1 s and
w 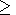 109 s
-1
aM = max |a(h,l,t)|
109 s
-1
aM = max |a(h,l,t)|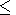 10-2;
so to obtain approximate solutions of this
equations, one should use the small perturbation method
[Kravtsov et al., 1983].
Actually, even the first approximation of this method
makes it possible to provide the needed accuracy of the
calculations of the main radiophysical effects occurring at the
propagation of the radio waves with
w
10-2;
so to obtain approximate solutions of this
equations, one should use the small perturbation method
[Kravtsov et al., 1983].
Actually, even the first approximation of this method
makes it possible to provide the needed accuracy of the
calculations of the main radiophysical effects occurring at the
propagation of the radio waves with
w 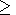 109 s
-1 through LREI.
109 s
-1 through LREI.
[20] To develop methods of calculations of radiophysical effects on the
basis of the analytical models of
N(h,l,t), one has to obtain the
dependence of its spatial coordinates
h and
l on the angular
coordinates of the object observation
( M and
F ) measured by a
radio engineering device and on the current distance
r (0 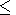 r
r 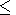 L )
under the given values of the geographical coordinates of the
explosion epicenter
( j1, l1 )
and the radio engineering device in
question
( j2, l2 ).
In Figure 1,
L designates the distance to the
observed object, the elevation angle
M and azimuth angle
F are
calculated from the horizontal plane in the point of the radio
engineering device location and from the direction to the explosion
in this plane, respectively. We have the following expressions for
the above indicated dependencies
L )
under the given values of the geographical coordinates of the
explosion epicenter
( j1, l1 )
and the radio engineering device in
question
( j2, l2 ).
In Figure 1,
L designates the distance to the
observed object, the elevation angle
M and azimuth angle
F are
calculated from the horizontal plane in the point of the radio
engineering device location and from the direction to the explosion
in this plane, respectively. We have the following expressions for
the above indicated dependencies
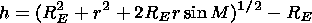 | (12) |
where
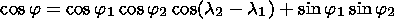 | (13) |
and
RE is the Earth radius.
[21] Solving equation (3) by the perturbation method the following
formulae were obtained for the refraction errors of the
measurements of the observed object angular coordinates
( D M = M- Mi,
D F= F- Fi )
[Gdalevich et al., 1963]:
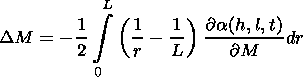 | (14) |
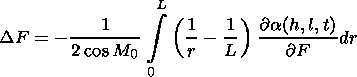 | (15) |
For the errors in the group delay
D Lgr the phase path length
D Lph and the component of the Doppler frequency shift caused by the
medium nonstationarity
D wn (they determine the error in the
determination of the distance and velocity of the observed object)
the following formulae are obtained in the first approximation:
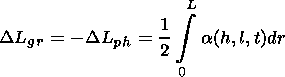 | (16) |
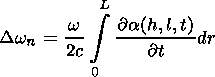 | (17) |
The medium parameter distributions
a (h,l,t) and their partial
derivatives with respect to the spatial coordinates and time are
determined by
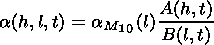 | (18) |
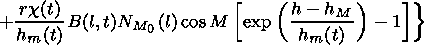 | (19) |
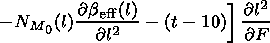 | (20) |
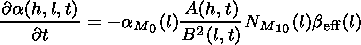 | (21) |
One can neglect the terms proportional to
h'(t) and
c' (t) in
equation (21) not exceeding the error of the order of a few percent.
In equations (18)-(21),
where
It should be noted that the Doppler shift of the frequency caused by
the influence of the medium is due to both the motion of the object
itself and nonstationarity of the medium along the radio wave
propagation path. The first component of this shift is of the same
order of magnitude as for the natural ionosphere [see, e.g.,
Kravtsov et al., 1983],
so here we consider only the second
component (17). Calculating the integrals included to equations
(14)-(17), each of them is split to two parts. The first is
determined by the LREI parameters and integration is performed
from
r1 to
rc. The calculation of the second part determined by the
parameters of the natural ionosphere is performed from
rc to
L. If
the condition
L < rc is fulfilled, integration in equations (14)-(17) is
limited only by the boundaries of the lower region and is performed
from
r1 to
L. The values of
r1 and
rc are given by
 | (22) |
into which either
h = 30 km or the height of the conjugation of the
lower region to the ionosphere
h = 90 km is substituted,
respectively.

|
|
Figure 4
|
[22] Solution of equation (4) for the field amplitude is written as
[Semenov, 1974]
Expanding the Jacobian
D(t ) in terms of the small parameter
am,
one can show
[Kravtsov et al., 1983]
that for a regular
inhomogeneous ionosphere the correction of the first order
D1(t ) is
small as compared to the zero approximation
D0(t ). Therefore
calculating the field amplitude
F in our case it is enough to take into
account only the spherical divergence of the rays and calculation of
the attenuation
d in the first approximation
( dt 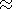 dr )
dr )
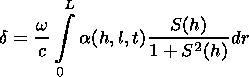 | (23) |
Here expression (18) is used for
a (h,l,t). Writing equation (23), we
did not neglect
S2 in comparison to 1 in the imaginary part of
e (see
equation (1)) because at heights of 30-40 km the inequality
n eff,en/w 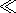 1,
generally speaking is not fulfilled for
w
1,
generally speaking is not fulfilled for
w 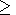 109 s-1.
According
to the experimental data
[Al'pert, 1972;
Gringauz, 1966]
obtained by different methods for
h
109 s-1.
According
to the experimental data
[Al'pert, 1972;
Gringauz, 1966]
obtained by different methods for
h 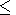 100 km the effective collision
frequency
n eff fairly well is described by the exponential dependence
(see Figure 4)
100 km the effective collision
frequency
n eff fairly well is described by the exponential dependence
(see Figure 4)
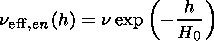 | (24) |
where the values
n0 =1.1 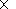 1011 s
-1 and
H0 = 7.1 km are fitted for the
n0 and
H0 parameters. Calculating the attenuation the usage of the
LREI analytical model (11) does not provide the relative error
required because its value is determined not only by the accuracy of
the
N(h,l,t) approximation, but depends on the quality of the
approximation of the product
N(h,l,t) n(h). To provide the
methodical error of the order of a few percent while calculating the
attenuation one should model the
N values by the methods
described by
Kozlov [1967, 1971],
Kozlov and Kudimov [1969],
and
Kozlov and Raizer [1966]
along the ray connecting
the radioengineering device and the observed object. In other
words, the initial electron concentrations are determined along the
ray in question and then the decrease of
N in these points is
calculated up to the time moment needed. Doing this one has to
obtain the distance
Ri from the explosion point to the points with the
coordinates
M,
F, and
ri at the ray having a height of
hi,
1011 s
-1 and
H0 = 7.1 km are fitted for the
n0 and
H0 parameters. Calculating the attenuation the usage of the
LREI analytical model (11) does not provide the relative error
required because its value is determined not only by the accuracy of
the
N(h,l,t) approximation, but depends on the quality of the
approximation of the product
N(h,l,t) n(h). To provide the
methodical error of the order of a few percent while calculating the
attenuation one should model the
N values by the methods
described by
Kozlov [1967, 1971],
Kozlov and Kudimov [1969],
and
Kozlov and Raizer [1966]
along the ray connecting
the radioengineering device and the observed object. In other
words, the initial electron concentrations are determined along the
ray in question and then the decrease of
N in these points is
calculated up to the time moment needed. Doing this one has to
obtain the distance
Ri from the explosion point to the points with the
coordinates
M,
F, and
ri at the ray having a height of
hi,
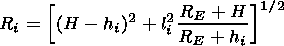 |
where
li is determined by equations (22) and (12). Further
calculation of the attenuation (23) is performed in a similar way to
the calculation of the integrals in equations (14)-(17). Such
approach provides the required methodical error in simulation of
the wave attenuation in LREI, however increases the time needed
for the calculations.

|
|
Figure 5
|
|
|
Figure 6
|
|
|
Figure 7
|

|
|
Figure 8
|
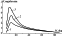
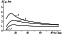
[23] Using the method described above, the calculations of the
attenuation, group delay, Doppler frequency shift and azimuthal
refraction as functions of the radiotechnical coordinates of the
object in the wide range of
H and
q were performed. The results
show that the main radiophysical effect influencing propagation of
the radio waves with
w 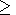 109 s-1 through LREI is the attenuation. For
the Doppler systems operating at frequencies
w
109 s-1 through LREI is the attenuation. For
the Doppler systems operating at frequencies
w 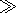 109 s-1, the
Doppler frequency shift reaching at
w=109 s-1 at
t
109 s-1, the
Doppler frequency shift reaching at
w=109 s-1 at
t 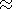 1 s the value of
D wL
1 s the value of
D wL 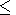 1 kHz
may present an exception. As an example,
Figures 5,
6,
7, and
8
show the values of these effects at the working frequency
w = 109 s-1 for the explosion with
q = 5000 kT at
H = 150 km,
distanced from the radio engineering device by
b = 335 km, at
different elevation angles of the observed object
M and
F = 10o.
The value of
b was found by
1 kHz
may present an exception. As an example,
Figures 5,
6,
7, and
8
show the values of these effects at the working frequency
w = 109 s-1 for the explosion with
q = 5000 kT at
H = 150 km,
distanced from the radio engineering device by
b = 335 km, at
different elevation angles of the observed object
M and
F = 10o.
The value of
b was found by
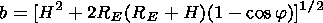 |

Citation: Semenov, B. I., V. V. Treckin, and S. I. Kozlov (2004), Influence of the lower region of the enhanced ionization produced by a space nuclear explosion on radio wave propagation, Int. J. Geomagn. Aeron., 5, GI1005, doi:10.1029/2003GI000053.
Copyright 2004 by the American Geophysical Union
Powered by TeXWeb (Win32, v.1.5).
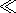 D H2/ 4b0 ), when one can
neglect the horizontal gradients. The latter situation takes place
during SNE of relatively small equivalents occurring at considerable
distances from the Earth when the LREI influence on the radio
wave propagation is insignificant. We here are interested in cases of
the strongest impact of LREI on the operation of radio systems
when one cannot separate the variables in equations (3) and (4) for
model (11). However, one can easily see
(see, e.g., Table 1 and
equations (2) and (11)) that under
t
D H2/ 4b0 ), when one can
neglect the horizontal gradients. The latter situation takes place
during SNE of relatively small equivalents occurring at considerable
distances from the Earth when the LREI influence on the radio
wave propagation is insignificant. We here are interested in cases of
the strongest impact of LREI on the operation of radio systems
when one cannot separate the variables in equations (3) and (4) for
model (11). However, one can easily see
(see, e.g., Table 1 and
equations (2) and (11)) that under
t 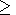 1 s and
w
1 s and
w 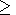 109 s
-1
aM = max |a(h,l,t)|
109 s
-1
aM = max |a(h,l,t)|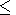 10-2;
so to obtain approximate solutions of this
equations, one should use the small perturbation method
[Kravtsov et al., 1983].
Actually, even the first approximation of this method
makes it possible to provide the needed accuracy of the
calculations of the main radiophysical effects occurring at the
propagation of the radio waves with
w
10-2;
so to obtain approximate solutions of this
equations, one should use the small perturbation method
[Kravtsov et al., 1983].
Actually, even the first approximation of this method
makes it possible to provide the needed accuracy of the
calculations of the main radiophysical effects occurring at the
propagation of the radio waves with
w 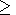 109 s
-1 through LREI.
109 s
-1 through LREI.

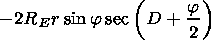
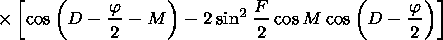
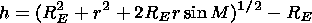
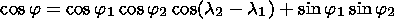
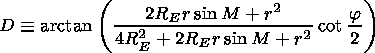
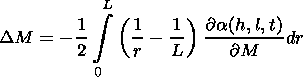
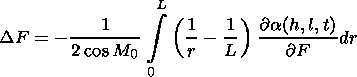
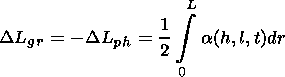
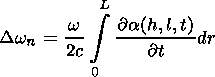
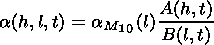
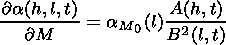
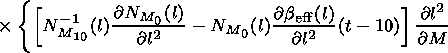
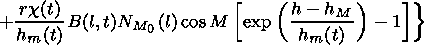
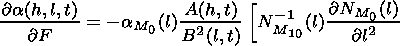
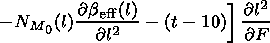
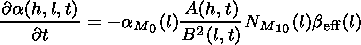
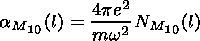
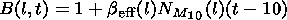
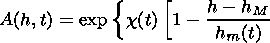
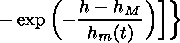
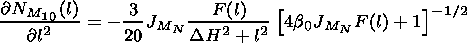
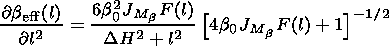
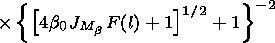
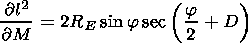
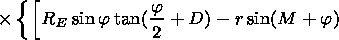
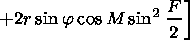
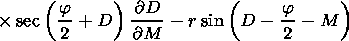
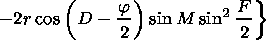
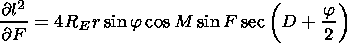
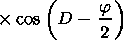
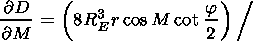
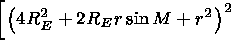



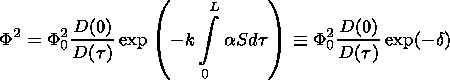
 dr )
dr )
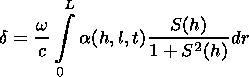
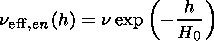
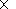 1011 s
-1 and
H0 = 7.1 km are fitted for the
n0 and
H0 parameters. Calculating the attenuation the usage of the
LREI analytical model (11) does not provide the relative error
required because its value is determined not only by the accuracy of
the
N(h,l,t) approximation, but depends on the quality of the
approximation of the product
N(h,l,t) n(h). To provide the
methodical error of the order of a few percent while calculating the
attenuation one should model the
N values by the methods
described by
Kozlov [
1011 s
-1 and
H0 = 7.1 km are fitted for the
n0 and
H0 parameters. Calculating the attenuation the usage of the
LREI analytical model (11) does not provide the relative error
required because its value is determined not only by the accuracy of
the
N(h,l,t) approximation, but depends on the quality of the
approximation of the product
N(h,l,t) n(h). To provide the
methodical error of the order of a few percent while calculating the
attenuation one should model the
N values by the methods
described by
Kozlov [




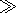 109 s-1, the
Doppler frequency shift reaching at
w=109 s-1 at
t
109 s-1, the
Doppler frequency shift reaching at
w=109 s-1 at
t