3. Algorithm Development

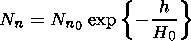
[12]  To develop effective algorithms (realized at modern computers) of calculation of the field distortions appearing during the radio wave propagation in the medium disturbed by the explosion, it is reasonable to create an analytical model of this medium. This model should provide calculation of the medium parameters and their partial derivatives in terms of spatial coordinates and time required for integration of equations (2) and (3) in any points of the considered region. The analysis of development of such models (including the use of rigid methods of the function approximation theory) has shown that the most acceptable for practice is use, as approximating dependencies, of solutions of the simplified physical problems. Such problems make it possible to feel the main features of parameter distribution in the artificial ionization region (e.g., in LREI) and at the same time contain a small number of constants fitted to get the best agreement of the numerical simulation results (in our case by the methods described by Kozlov [1967, 1971], Kozlov and Kudimov [1969], and Kozlov and Raizer [1966]). Moreover, using fairly accurate methods of calculations of the main radiophysical effects, sometimes it is possible to estimate the unknown constants of the analytical model from the experimental data available.

[13]  The distribution of the electron concentration in the lower atmosphere produced by the X ray and penetrating radiation of SNE is symmetrical relative the vertical axis. Therefore the LREI analytical model should depend on time and two spatial coordinates: the altitude h and distance l to the epicenter axis (Figure 1). For the approximation of the results of N(t) calculations within LREI it is reasonably to use the dependencies which are obtained as a result of the solution of the simplified problem of falling of monochromatic emission at the angle q to the vertical on a flat layer of the exponential atmosphere with constant scale height H_c containing particles of only one type ( N_n (h=0) =N_n0 )

The number of the formed pairs of ionized particles is determined by the energy absorbed per second by the gas volume unit with the effective cross section s is called the ionization rate J. To obtain the approximating dependence N(t) we use the equations the Chapman layer [Al'pert, 1972], in particular (taking N = N_i⁺ ) the ionization equation balance:

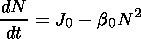(5)

with the recombination coefficients b₀, cm^-3 s^-1 and ionization rate J₀, cm^-3 s^-1. Then in the quasi-stationary conditions ( dN/dt 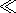b₀ N² ) the vertical distribution of the electron concentration takes the form

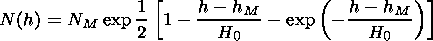(6)

The N(h) maximum N_M is determined by the condition dJ₀/dh = 0 and is located at the altitude h_M = H₀ ln (N_n0 s H₀ secq ). Thus, to describe h_M(l), the dependence

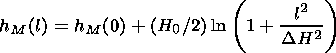where D H = H - h_i(0), may be used. To take into account the deformation of the N(h) vertical profile with time, we substitute the constants 1/2 and H₀ in equation (6) by the dependencies c(t) and h_m(t).

[14]  Since the N level in LREI quickly decreases, the values of the effects caused by this region and by the ionosphere [see, e.g., Kravtsov et al., 1983] become of the same order of magnitude. That is why one has to obtain a conjugation of the LREI analytical model to the ionospheric model. As the latter, the global phenomenological model [Ching and Chiu, 1973; Chiu, 1975] corrected for polar latitudes [Vlaskov and Ogloblina, 1981] is used. The N distributions within the altitude interval h=90-1000 km obtained at 50 vertical sounding ionospheric stations present an experimental basis of the Ching and Chiu [1973] model. The observations were performed in 1957-1970, this interval including the time of carrying out nuclear explosions. The analytical expressions describing the polar part of the model were specified by Vlaskov and Ogloblina [1981] on the basis of 11 high-latitude stations of the Northern Hemisphere.

[15]  We are interested in the intervals t 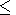100 s after the explosion moment. For these intervals one may neglect by the disturbance of the ionosphere by acoustic gravity waves propagating with a velocity less than 1 km s^-1 [Peterson, 1967], because the region of their influence would not considerably exceed the dimensions of the ionized region of the explosion [see, e.g., Lobolev, 1997a, 1997b].

[16]  The results of the calculations [Kozlov, 1967, 1971; Kozlov and Kudimov, 1969; Kozlov and Raizer, 1966; Kozlov et al., 1982] show that a few minutes after the explosion moment independently on l the maximum in N_M is formed at a height of h_M(0) 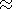70 km. The performed studies show that the influence of the geometrical parameters of the medium on the values of the radiophysical effects is significantly (by about an order of magnitude) less than the influence of the gradients of the maximum electron concentration [Misura, 1973]. So taking into account the error in N calculations, taking into account of the h_m dependence on l looses sense. To describe the N(l) distribution within LREI, it is enough to approximate the electron concentration distribution in the maximum N_M(l). Neglecting the absorption of the radiation in the upper atmospheric layers down to the height of the nuclear explosion and taking into account the spherical divergence of the explosion radiation, we obtain the dependence of J₀ at the height h_M

(7)

The initial distribution of the electron concentration at this height formed by the instant radiation will be N_M(l) = N_M0 (0) F(l). If the ionization source is "switched off" ( J₀=0 ), a solution of equation (5) with the found initial conditions is written in the form

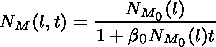(8)

If one takes into account in equation (5) the variations with time of the intensity of gamma radiation of the fission fragments, it would lead to a substitution in equation (8) of the recombination coefficient b₀ by its effective value b _eff(l).

[17]  Analysis of the fission fragments (e.g., after the "Starfish" explosion) shows [D'Arcy and Colgate, 1965] that since the first minutes the time decrease of the gamma radiation varies from t^-2.6 in the energy interval 9-13 MeV [see D'Arcy and Colgate, 1965, Figure 14] to t^-2, t^-1.5, and t^-1.2 for the energies 2.6-4, 0.9-2.6, and 0.02-0.9 MeV, respectively [D'Arcy and Colgate, 1965, Figure 9]. So in the simplified problem considered here we take the variation of the ionization source in the form J_M0(l)/t², assuming

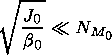In this case integrating (5) we obtain for b _eff(l)

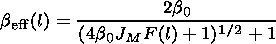(9)

As a basic spatial distribution of N at a height h_M it was more convenient to take not the initial distribution N_M0 (l), but the N_M10 (l) distribution for the 10 s time moment

(10)

Then the spatial-time distribution of the electron concentration in LREI may be described by

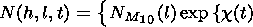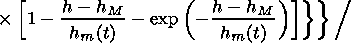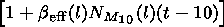(11)

The values of the J_M constants in (9) and (10) we will further assume to be different J_M J_Mb and J_M J_MN, respectively.

Figure 2

Figure 3

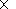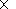[18]  As an example, Figures 2 and 3 show the results of the approximation by dependencies (9)-(11) of the N calculations in LREI for the SNE with q=5000 kT and H =150 km. Points correspond to the numerical simulations [Kozlov, 1967, 1971; Kozlov and Kudimov, 1969; Kozlov and Raizer, 1966; Kozlov et al., 1982]. The constants fitted for approximation are J_MN =13.16 10¹¹ s cm ^-1, J_{M b} =35.36 10¹¹ s cm ^-1, b₀ = 2.9 10^-7 cm ³ s ^-1, h_M = 70 km, and D H = 100 km. For c and h_M the following dependencies are taken:

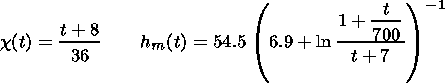where t is measured in seconds.