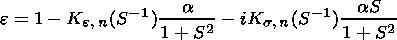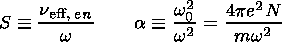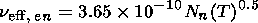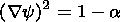INTERNATIONAL JOURNAL OF GEOMAGNETISM AND AERONOMY VOL. 5, GI1005, doi:10.1029/2003GI000053, 2004
2. Evaluation of the Impact of the SNE Regions
[7] The problems of evaluation of the impact of SNE artificial
ionization regions on the operation of radioelectronic systems due
to its complicity should be solved in two stages. At the first stage,
as a rule, the parameters of the medium disturbed by the explosion
are studied. First of all, fairly exact methods of solution of the
nonstationary equation of the transfer of SNE ionizing radiation in
the inhomogeneous atmosphere are developed
[see Lobolev, 1997a,
1997b;
Kukhtevich and Mashkovich, 1979].
Then the problems of ionization and kinetics of the
plasma parameters of the lower atmospheric layers by the X ray
and penetrating radiation are considered.
[8] The calculation of the LREI SNE parameters requires taking into
account a large number of photochemical processes involving tens
of chemical constituents. Variations in the electron concentration
N(t) and ion composition in time are looked for as a result of
integration of the system of differential equations of continuity for
each parameter. The initial conditions are formed under action of
gamma quanta, neutrons, and X rays with the formation rates of the
constituents determined by the fission fragments and beta particles.
In the general case to take into account correctly the influence on
N(t) of minor neutral constituents one has to include into the
equations (together with the chemical reactions) the transport terms.
Integration of such a system of differential equations of a
"rigid type" needs large resources of computer time, so for its solution
sometimes one attracts special computing methods accelerating the
computation process and introducing additional errors
[see, e.g., Kozlov et al., 1982].
The approach realized by
Kozlov [1967, 1971],
Kozlov and Kudimov [1969], and
Kozlov and Raizer [1966]
provided development of methods and calculation
algorithms which made it possible to simulate numerically
parameters of the lower atmosphere disturbed by the explosion.
The parameters agree satisfactorily with the experimental data.
Actually, for the frequency range from 100 to 1000 MHz and more
where the vast majority of the radiolocation, radio navigation, and
radio communication equipment operates, the method provides the
accuracy of
N(t) calculations within LREI better than a few tens of
percent. The problem of evaluation of the modeling accuracy of the
disturbed by the explosion medium (where radio waves are
propagating) is far from being trivial and we will come back to this
problem at the end of the paper. Here we note that to provide a
possibility to control the
N(t) simulation accuracy in the LREI on
the basis of radiophysical measurements available one has to
develop methods of calculation of radiophysical effects with the
error less than a few percent.
[9] The studies of the second stage of the considered problem of
evaluation of the SNE impact on operation of radioelectronics
systems are reduced to solving of two problems. As a preliminary
step one has to present the macroscopically continuous
components of the dielectric permeability
eik in terms of parameters
characterizing the plasma, that is in terms of the concentration of
electrons ( N ), ions ( Ni ), and neutral particles ( Nn ), as well as the
distribution of their velocities. The second step involves solution of
the Maxwell equations with the given
eik (r,t) functions and the
range of the
w cyclic frequencies.
[10] The plasma in LREI may be considered as a gas
((kT)/(e2N1/3) 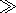 1 ),
so to look for general expression for
eik one should use the
method of the kinetic equation which includes also the terms taking
into account variations of the distribution function due to the
processes of ionization and recombination. As for the initial data for
the plasma parameters, the results of the LRIE calculations for the
wide range of explosion altitudes and TNT equivalents of nuclear
charges obtained by
Kozlov [1967, 1971],
Kozlov and Kudimov [1969], and
Kozlov and Raizer [1966]
are used. Table 1 based on
the results of these publications shows (for the case
q=5000 kT,
H = 150 km and
w = 109 s
-1 close to the worst case) the calculations
of the LREI plasma parameters along the vertical from the
explosion epicenter for the time moment
t=1 s. Moreover, the
vertical profiles of the effective collision frequencies of ions with
neutral particles
( n eff, in ),
electrons with neutral particles
( n eff, en ),
and
electrons with ions
( n eff, ei ),
are also shown. The corresponding
absorption coefficients of radio waves (see equation (2)):
m
1 ),
so to look for general expression for
eik one should use the
method of the kinetic equation which includes also the terms taking
into account variations of the distribution function due to the
processes of ionization and recombination. As for the initial data for
the plasma parameters, the results of the LRIE calculations for the
wide range of explosion altitudes and TNT equivalents of nuclear
charges obtained by
Kozlov [1967, 1971],
Kozlov and Kudimov [1969], and
Kozlov and Raizer [1966]
are used. Table 1 based on
the results of these publications shows (for the case
q=5000 kT,
H = 150 km and
w = 109 s
-1 close to the worst case) the calculations
of the LREI plasma parameters along the vertical from the
explosion epicenter for the time moment
t=1 s. Moreover, the
vertical profiles of the effective collision frequencies of ions with
neutral particles
( n eff, in ),
electrons with neutral particles
( n eff, en ),
and
electrons with ions
( n eff, ei ),
are also shown. The corresponding
absorption coefficients of radio waves (see equation (2)):
m 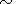 (w/c) a S/(1+S2) both for the Maxwell velocity distribution of
particles
( min, men, and
mei ), characterized by the temperature
T and
for distributions different from the equilibrium distributions due to
the ionization processes
(m*en )
are also presented in Table 1. One
can easily see in Table 1 that within the height interval 30-90 km
the values of
e ik are determined by the electron distribution
fe (r, v, t),
and the distribution of their velocities may be considered as a
Maxwell distribution with acceptable accuracy. Taking into account
that for
w
(w/c) a S/(1+S2) both for the Maxwell velocity distribution of
particles
( min, men, and
mei ), characterized by the temperature
T and
for distributions different from the equilibrium distributions due to
the ionization processes
(m*en )
are also presented in Table 1. One
can easily see in Table 1 that within the height interval 30-90 km
the values of
e ik are determined by the electron distribution
fe (r, v, t),
and the distribution of their velocities may be considered as a
Maxwell distribution with acceptable accuracy. Taking into account
that for
w 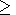 109 s-1 the input of LREI into the polarization
distortions is negligibly small
[Batyr et al., 1996],
to describe
macroscopically continuous properties of the plasma, one can use
the complex permeability
e = e' - ie'' = 1/3 Sp eIk (under
wH/ w = |e| HE / mcw
109 s-1 the input of LREI into the polarization
distortions is negligibly small
[Batyr et al., 1996],
to describe
macroscopically continuous properties of the plasma, one can use
the complex permeability
e = e' - ie'' = 1/3 Sp eIk (under
wH/ w = |e| HE / mcw  0 )
0 )
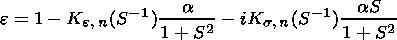 | (1) |
Here
Ke,n and
Ks, n are the functions obtained in the scope of the
kinetic theory

|
|
Figure 1
|
[see, e.g., Ginzburg, 1967, Figures 6.1 and 6.2];
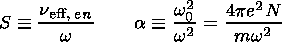 | (2) |
where
e and
m are the charge and mass of an electron,
c is the
light velocity,
HE is the Earth magnetic field, and
The results of the performed estimations (see Table 1)
show that
for
w  109 s-1 with the acceptable error not exceeding a few
percent one can take
Ke,n = Ks,n
109 s-1 with the acceptable error not exceeding a few
percent one can take
Ke,n = Ks,n  1 and limit the study by the
consideration of the permeability in the scope of the elementary
theory
[Ginzburg, 1967].
1 and limit the study by the
consideration of the permeability in the scope of the elementary
theory
[Ginzburg, 1967].
[11] As the next step in the study of the problem of radio wave
propagation in plasma one has to find solution of the Maxwell
equations for the given spatial-time distributions of
e(r, t) having
certain scales of nonstationarity and spatial nonuniformity. One can
show that for the LREI plasma the conditions of quasi-stationarity
and quasi-uniformity are fulfilled already at
t 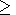 1 s and
w
1 s and
w 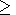 109 s
-1.
The characteristic scales of irregularities ( z )
of the artificial ionization
regions for nuclear explosions are from a few kilometers to tens of
kilometers, so in the
l wavelength range we are interested in the
value of the
l/z ratio does not exceed portions of a percent. One
can demonstrate
[Semenov, 1974]
that in our case the solution of
the Maxwell equations in the zero approach of the geometric optics
is reduced to integration of three equations: eiconal
y
109 s
-1.
The characteristic scales of irregularities ( z )
of the artificial ionization
regions for nuclear explosions are from a few kilometers to tens of
kilometers, so in the
l wavelength range we are interested in the
value of the
l/z ratio does not exceed portions of a percent. One
can demonstrate
[Semenov, 1974]
that in our case the solution of
the Maxwell equations in the zero approach of the geometric optics
is reduced to integration of three equations: eiconal
y
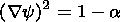 | (3) |
of the transport for the electric field amplitude
F (k=w/c )
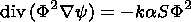 | (4) |
and the rotation angle of the polarization plane which (as it has been
noted above) one may not consider for the propagation through
LREI of radio waves with
w 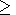 109 s-1. Integrating equations (3) and
(4), one can calculate the electromagnetic field and the main
radiophysical effects with the accuracy up to the terms
109 s-1. Integrating equations (3) and
(4), one can calculate the electromagnetic field and the main
radiophysical effects with the accuracy up to the terms
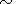 0 (l/z),
that is, the methodical error of the calculations of radio wave
distortions is negligibly small.
0 (l/z),
that is, the methodical error of the calculations of radio wave
distortions is negligibly small.

Citation: Semenov, B. I., V. V. Treckin, and S. I. Kozlov (2004), Influence of the lower region of the enhanced ionization produced by a space nuclear explosion on radio wave propagation, Int. J. Geomagn. Aeron., 5, GI1005, doi:10.1029/2003GI000053.
Copyright 2004 by the American Geophysical Union
Powered by TeXWeb (Win32, v.1.5).
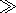 1 ),
so to look for general expression for
eik one should use the
method of the kinetic equation which includes also the terms taking
into account variations of the distribution function due to the
processes of ionization and recombination. As for the initial data for
the plasma parameters, the results of the LRIE calculations for the
wide range of explosion altitudes and TNT equivalents of nuclear
charges obtained by
Kozlov [1967, 1971],
Kozlov and Kudimov [1969], and
Kozlov and Raizer [1966]
are used. Table 1 based on
the results of these publications shows (for the case
q=5000 kT,
H = 150 km and
w = 109 s
-1 close to the worst case) the calculations
of the LREI plasma parameters along the vertical from the
explosion epicenter for the time moment
t=1 s. Moreover, the
vertical profiles of the effective collision frequencies of ions with
neutral particles
( n eff, in ),
electrons with neutral particles
( n eff, en ),
and
electrons with ions
( n eff, ei ),
are also shown. The corresponding
absorption coefficients of radio waves (see equation (2)):
m
1 ),
so to look for general expression for
eik one should use the
method of the kinetic equation which includes also the terms taking
into account variations of the distribution function due to the
processes of ionization and recombination. As for the initial data for
the plasma parameters, the results of the LRIE calculations for the
wide range of explosion altitudes and TNT equivalents of nuclear
charges obtained by
Kozlov [1967, 1971],
Kozlov and Kudimov [1969], and
Kozlov and Raizer [1966]
are used. Table 1 based on
the results of these publications shows (for the case
q=5000 kT,
H = 150 km and
w = 109 s
-1 close to the worst case) the calculations
of the LREI plasma parameters along the vertical from the
explosion epicenter for the time moment
t=1 s. Moreover, the
vertical profiles of the effective collision frequencies of ions with
neutral particles
( n eff, in ),
electrons with neutral particles
( n eff, en ),
and
electrons with ions
( n eff, ei ),
are also shown. The corresponding
absorption coefficients of radio waves (see equation (2)):
m 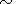 (w/c) a S/(1+S2) both for the Maxwell velocity distribution of
particles
( min, men, and
mei ), characterized by the temperature
T and
for distributions different from the equilibrium distributions due to
the ionization processes
(m*en )
are also presented in Table 1. One
can easily see in Table 1 that within the height interval 30-90 km
the values of
e ik are determined by the electron distribution
fe (r, v, t),
and the distribution of their velocities may be considered as a
Maxwell distribution with acceptable accuracy. Taking into account
that for
w
(w/c) a S/(1+S2) both for the Maxwell velocity distribution of
particles
( min, men, and
mei ), characterized by the temperature
T and
for distributions different from the equilibrium distributions due to
the ionization processes
(m*en )
are also presented in Table 1. One
can easily see in Table 1 that within the height interval 30-90 km
the values of
e ik are determined by the electron distribution
fe (r, v, t),
and the distribution of their velocities may be considered as a
Maxwell distribution with acceptable accuracy. Taking into account
that for
w 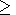 109 s-1 the input of LREI into the polarization
distortions is negligibly small
[Batyr et al., 1996],
to describe
macroscopically continuous properties of the plasma, one can use
the complex permeability
e = e' - ie'' = 1/3 Sp eIk (under
wH/ w = |e| HE / mcw
109 s-1 the input of LREI into the polarization
distortions is negligibly small
[Batyr et al., 1996],
to describe
macroscopically continuous properties of the plasma, one can use
the complex permeability
e = e' - ie'' = 1/3 Sp eIk (under
wH/ w = |e| HE / mcw  0 )
0 )