Non-resonant wave-particle interaction due to the ion Weibel instability in the Earth neutral sheet and the current disruption problem

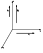
A. M. Sadovski and A. A. Galeev

Space Research Institute of Russian Academy of Sciences Moscow, Russia

Contents

Abstract

1. Introduction

Instabilities due to the cross-field current which can arise in different regions of the solar-terrestrial environment have been discussed by many authors. Investigation of such kind of instabilities is primarily bound up with the processes in collisionless shock waves both in laboratory and space plasmas and in the geomagnetic tail. Particular emphasis for the parameters relevant to the Earth's neutral sheet has been placed on the modified two-stream instability and on the lower hybrid drift instability (see for details and references Lui et al. [1991]). In the discussion of aforementioned instabilities the effects of ions was assumed to be negligible because of their heavy mass. However Chang et al. [1990] have shown that in general ion response would play a significant role in exiting electromagnetic waves directed almost parallel to the ambient magnetic field in the case of unmagnetized ions and magnetized electrons. They have found that including the ion response can change significantly the growth rate and a purely growing mode exists. The physical properties of this purely growing mode resemble that of the classical Weibel instability for the electron streams in unmagnetized plasma [Weibel, 1959] and no wonder that this mode was named as Ion Weibel Instability (IWI) [Chang et al., 1990]. Numerical investigation of the dispersion equation for this instability showed that it exists in high beta regimes as in the Earth's neutral sheet. That is the reason why IWI was assumed to be helpful in the explanation of a substorm onset. A substorm onset is characterized by the recovery of the magnetic field lines from a tail-like to a dipolar configuration (dipolarization). This phenomenon can be interpreted in terms of a reduction of the cross tail current intensity (current disruption) [Lui, 1996; Lui et al., 1991, 1993; Wu, 1992]. In last decades the mechanism describing how current reduction occurs was one of the overwhelmingly important problem for the understanding of the substorm initiation and a considerable amount of research has been carried out to construct the theoretical model for current disruption.

Several instabilities and mechanisms has been proposed to accomplish the current disruption (see for discussion and references [Lui, 1996; Lui et al., 1991] such as the tearing instability, the ballooning instability, the thermal catastrophe model, the coupling between the magnetosphere and the ionosphere, and the model based on the cross-current instabilities. The preliminary analysis of the latest mechanism was done by Lui et al. [1991]. They have introduced the model combining several types of instabilities driven by a current flowing perpendicular to the ambient magnetic field. Among these cross-field current instabilities IWI plays the role of no small importance. The function of this instability is to provide anomalous resistivity in order to modify significantly the local current density and supply a collisionless dissipation necessary to initiate the fast magnetic reconnection or facilitate the development of other instability process in the magnetosphere tail for a example tearing instability [Lui, 1996].

Exhaustive derivation of the dispersion tensor elements and the linear dispersion equation for a wave vector parallel to the ambient magnetic field (  k = k z ) can be found in [Wu et al., 1992]. The authors also generalized the paper by Chang et al. [1990] for the situation of magnetized ions. The extensive numerical analysis of the dispersion relation was done in [Lui et al., 1991; Wu et al., 1992; Yoon et al., 1992]. Nonlinear evolution of IWI was discussed by Yoon [1991] for the case of a quasiperpendicular collisionless shock and Lui et al. [1993] for the parameters related to the Earth's neutral sheet. The numerical solution of quasilinear equation of IWI was performed using moments of kinetic equation. However in both papers the ion distribution was taken to retain its original functional form in time and only temperatures and drift velocity change.

Below we perform the analytical treatment of the quasilinear kinetic equation for IWI to find how the ion distribution function changes and solve the dynamic equations for the moments to obtain the saturation level of this instability.

The organization of paper is as follows. In Section 2 we briefly survey the physical model and the linear dispersion relation. Section 3 is devoted to the derivation of quasilinear equation and the determination of ion distribution function. In Section 4 we perform the moment kinetic equations for the ion distribution and show the results obtained from our calculation.

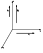
Figure 1

2. Linear Dispersion Relation

Let us at first briefly describe the physical model and the geometrical configuration based on [Wu et al., 1992, Yoon, 1991]. The basic assumption following from [Lui et al., 1991, 1993; Yoon, 1991] is that the ions are unmagnetized and allowed to drift with the initial drift velocity v₀=v₀ y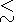 v_Ti perpendicular to the ambient magnetic field B₀ = B₀z (Figure 1). Here x,y,z are the basis vectors of the Sun-Earth magnetic coordinate system, in which the x axis is directed along Earth-Sun line, z axis is in the South-North direction and y axis is chosen to form right-hand triple. The electrons are treated fully magnetized and stationary. In terms of mathematical relations this conditions may be stated as:

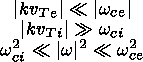(1)

where v_Te=(2T_e/m_e)^1/2 and v_Ti=(2T_i/m_i)^1/2 are the electron and the ion thermal velocity respectively, T_j is the temperature w_cj is the cyclotron frequency of jth species. To simplify the analysis we take electrons and ions to be isotropic and use the Maxwellian distribution function for the electrons and the drifting Maxwellian distribution for the ions:

(2)

As mentioned above the derivation of the dispersion tensor elements and linear dispersion equation for the wave vector parallel to the ambient magnetic field (  k = k z ) was done by [Wu et al., 1992]. Neglecting the displacement current and using the aforementioned conditions one can easily obtain the components of the dispersion matrix D_ij and the linear dispersion equation in the form [Wu et al., 1992; Yoon, 1991]

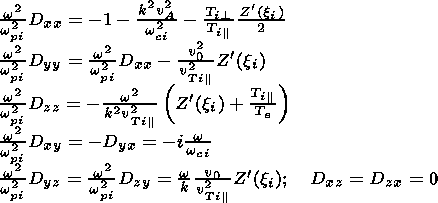(3)

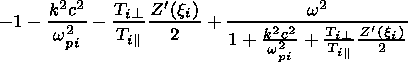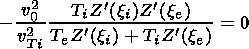(4)

where w_pi is the ion plasma frequency, c is the speed of light and Z is given by

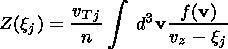(5)

and for the Maxwellian distribution coincides with the well-known plasma dispersion function. The "prime" defines the first derivative of this function over x_j. The argument of Z are defined by: x_j = w/k v_Tj.

Similarly to the papers [Lui, 1991, 1993] we consider the Ion Weibel instability for the two sets of plasma parameters relevant to the neutral sheet of the Earth's magnetotail. The first set corresponds to the inner edge of the Earth neutral sheet: T_i/T_e = 4, T_i=12 keV, n_e=n_i=n=0.6 cm^-3, B₀=25 nT and the second corresponds to the midtail region: T_i/T_e 10, T_i=2 keV, n_e=n_i=n=0.3 cm^-3, B₀=5 nT [Baumjohann, 1993; Lui, 1991, 1993]. Here n_j is the density of j th species. Since for the both regions T_e/T_i and v_Ti/v_Te are much less than unity, they can give only small corrections and below will be omitted.

The obtained dispersion equation supports the purely growth mode Rew = 0 ) and making use of the asymptotic expansion for Z(x_j) in the limit of |x_j|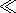 1 we find to leading order from (4) the resulting growth rate:

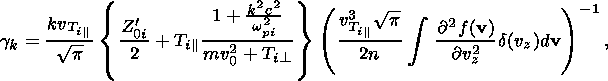(6)

where m is the mass of the ions, and Z_0i = v_Ti²2n f( v)v_z v_zd³ v is the first term of expansion of Z(x_i) in power series in x_i.

From (6) it follows that for the any function f having maximum at v_z=0

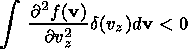(7)

we can write the condition for the existing of the instability in form:

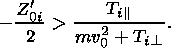(8)

For a purely growing instability, as in our case, the quasilinear theory is applicable only if kDv_z 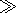g where Dv_z is the range in the velocity space most strongly affected by diffusion [Biskamp et al., 1970; Galeev and Sagdeev, 1979]. In the case Dv_z v_Ti we can write that for the IWI quasilinear theory is valid under the condition

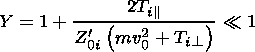(9)

One can see that this condition is fulfilled for the parameters cited above.

3. Derivation of Quasilinear Kinetic Equation

According to results obtained by Yoon [1991] the saturation level of the unstable Ion Weibel modes is high enough when only the ions are allowed to drift perpendicular to the ambient magnetic field. Therefore in quasilinear analysis we can neglect contribution of the magnetized electrons and write the quasilinear kinetic equation for the ion distribution function in the form:

(10)

Here the angular brackets denote the averaging over the random phases of the fluctuating Fourier components of electric E_k and magnetic B_k fields, * denotes the complex conjugation and df_k represents the spectral component of the perturbed distribution function given by an integral over the particles' trajectories:

(11)

where v_x(t)=v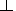 sin(q-w_cit), v_y(t)=v₀+v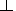 cos(q-w_cit), v_z(t)=v_z, v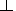²=v_x²+v_y², q is the gyrophase angle. Using the Maxwell equation we express the spectral components of electric field E_k in terms of spectral components of the magnetic field B_k:

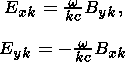(12)

where subscripts x and y denote spatial components of the fields.

The expression for the perturbed part of the distribution function df_k is obtained by integrating over the particles trajectories in equation (11):

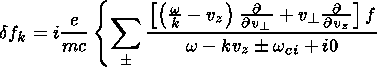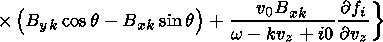(13)

Here the small electrostatic wave energy was neglected.

The differential operator in front of df_k in the equation (10) can be written as:

(14)

Using the expressions (13) and (14) and averaging over the gyrophase angle q we rewrite the quasilinear equation for the ion distribution function:

(15)

The time evolution of the magnetic field fluctuations is described by the equation:

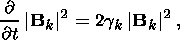(16)

where the growth rate of purely growing Ion Weibel instability g_k is determined by (6). From the dispersion matrix (3) one can easily obtain that

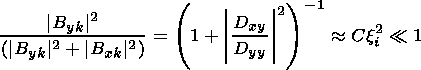i.e. a polarization of the unstable mode is almost linear so |B_yk|² can be omitted within the accuracy of calculations (see also [Wu et al., 1992]).

Above we have assumed that the ions are treated as unmagnetized, so we can use the limit w_ci 0 in the kinetic equation and rewrite (15):

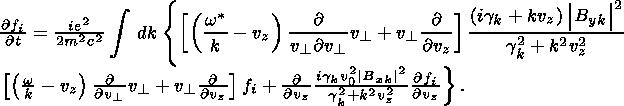(17)

Although the equation (17) describes the non-resonant wave interactions with all background ions, the efficiency of such interactions is different for different parts of the ion distribution. The main effect comes from the strong diffusion for v_z v_Ti. f_i can changes significantly in the region of small v_z whereas the average values such as T, T, v₀ vary slightly in the limit of Y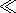 1. Thus for small v_z equation (17) may be rewritten keeping only two last terms in the right-hand side.

(18)

Taking the integral over v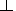 and introducing the new variable

we reduce (18) to the simple form [Biskamp et al., 1970; Galeev and Sagdeev, 1979]:

(19)

The equation (19) has an analytical solution in terms of the initial reduced ion distribution function (2). The solution may be written as [Biskamp et al., 1970]:

(20)

where J_n(x) is Bessel function of the first kind.

As a consequence from the equation (20) the plateau forms on the ion distribution function in the vicinity of v_z=0 with growth of the wave energy. The wave energy increases as long as the ion distribution remains unstable to the excitation of oscillations in other words while the parameter Y>0 (9).

4. Moment Kinetic Equations

The evolution equations for the drift velocity and the perpendicular and parallel temperatures may be found directly from (10)-(14) by taking the appropriate moments. (The consideration of this method is rigorously made in [Davidson et al., 1972; Shapiro and Shevchenko, 1964].) Taking the results obtained in paper [Yoon, 1991]:

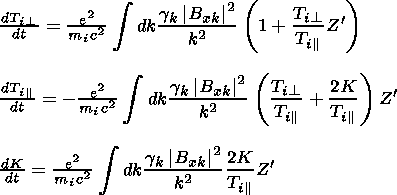(21)

where K=m_iv₀²/2 and Z is defined by (5).

Using the expansion of Z(x_i) in power series and taking only the first expansion terms we arrive to the system of differential equations describing the evolution of moments of the ion distribution function in terms of h:

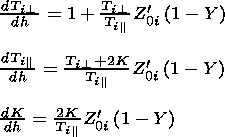(22)

For the obtained distribution function (20) the dependence of Z_0i(h) takes the form:

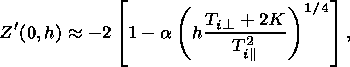(23)

where a is a constant 1.

On the saturation stage of the instability g_k 0 and from (9) we obtain:

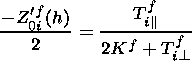(24)

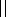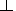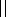where the superscript f denotes the final values of parameters. Let us assume T_i= T_i=T_i for the sake of simplicity and set T_i^f = T_i + d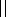T_i, T_i^f = T_i + dT_i, K^f= K₀ + dK. It is evidently that the contributions from dT_i, dT_i, dK in (24) are of the order of h/T1 and may be neglected in comparison with the contribution from Z_0i h^1/4/T^1/4. As a result we find:

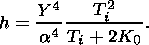(25)

Neglecting terms of higher order of Y and replacing T_i, T_i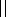, K by their initial values in the right-hand side of equations (22) that also corresponds to omitting terms of the higher order of Y, we find:

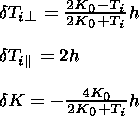(26)

As can be seen from the definition of h and equation (6) the value of wave energy has the next order in Y. Assuming that the main contribution to the wave energy comes from the value of the wave vector k_m =(w_ci/v_A) {Y[3(1-Y)]}^1/2, when the growth rate has its maximum we can estimate the wave energy as:

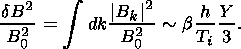(27)

Here we normalize dB² on the value of external magnetic field energy B₀²/8p.

Figure 2

Figure 3

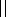Figures 2 and 3 demonstrate saturation values of the drift velocity v₀^f, parallel temperature T^f and perpendicular temperature T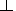^f normalized on its initial values as the functions of v₀/v_Ti. Within the accuracy of analysis the relative changes of the appropriate moments is equal both for the inner edge and for the midtail. As would be expected the excitation of the pure growing mode results in the growth of the parallel temperature due to the reduction of the cross-field current value. However the value of the perpendicular temperature remains almost unchanged that justifies assumption described above.

Figure 4

Figure 4 illustrates the wave energy for the two parts of the Earth's neutral sheet: (a) for the inner edge and (b) for the midtail. The amplitude of the fluctuating magnetic field for the case (b) is greater than for the case (a) but one should take into account that the value of b is greater for the midtail case.

At the end of this part it may be useful to estimate the anomalous resistivity, which is associated with the nonlinear development of instability. The anomalous resistivity may be determined as in [Galeev and Sagdeev, 1979]. A friction force results in the change of the particle momentum and a friction work is gone to the heating of ions, so we can write:

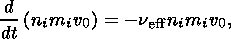(28)

where using (22) n _eff is defined as:

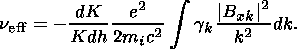(29)

Using the upper estimate in (29) by taking the maximum value of g_k we obtain with the help of (23):

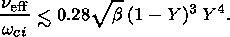(30)

The anomalous resistivity h _an is determined by:

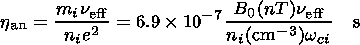(31)

Using parameters for the inner edge and the midtail we obtain for the highest value of the drift speed ( v₀=v_Ti ) that h _an (inner edge) 1.2 10^-7 s and h _an (midtail) 7 10^-8 s. These values give the anomalous resistivity more than one order less than obtained in paper [Lui et al., 1993]. Moreover the obtained values is out of the range of anomalous resistivity deduced to be present in the active regions of the magnetotail during substorm (see [Lui, 1996; Lui et al., 1993] for details).

5. Conclusion

The goal of our investigation was to study the general properties of the Ion Weibel Instability for plasma parameters related to the Earth's neutral sheet. The obtained results have shown that the saturation level of this instability is reached due to the formation of the plateau on the reduced ion distribution function. The evolution of the IWI has the physical and formal similarity with the evolution of instabilities with anisotropic temperatures in magnetic field (see, for example, [Shapiro and Shevchenko, 1964]. In both cases the evolution accompanies by the increasing of the parallel temperatures due to the transverse energy. The criterion of validity of the quasilinear theory is reduced to the smallness of deviation of the plasma parameters from the critical values corresponding to the instability threshold. These critical values may be easily obtained from (24).

The saturation level of IWI depends on the values of the drift velocity and plasma parameters. For the set of parameters typical for the neutral sheet the values of the moments of the ion distribution on saturation stage is much less then the values obtained earlier in papers [Lui et al., 1993] where the equations for the evolution of the moments was solved numerically. Even for v₀=v_Ti, when the changes of plasma parameters are the highest, the drift velocity and parallel temperature vary in magnitude only on ~5.8% and ~17% respectively. It is about 4.5 times less then the values obtained by Lui et al. [Lui et al., 1993]. Such discrepancy can be explained by the fact that in numerical solution it was assumed that the ion distribution retains its original forms, i.e. it was assumed to be Maxwellian for all time, and only the global plasma parameters was changed. Mathematically it means that the numerical value of the function Z_0i in equations (9) and (24) does not change during the instability evolution. However just the dependence Z_0i on h gives the greatest contribution in (24).

In our calculation we limit ourselves by the parallel propagation of waves but there is no any reasons that taking into account the transverse component of the wave vector may heavily changes the saturation level. However the presence of the transverse component of the wave vector results in great complication of calculations and the investigation of such instability in the case of oblique wave propagation can serve as a theme for future work.

The calculated value of the drift velocity is less than the obtained from the experimental data from IMP 6 and ISEE 1 which is estimate as ~25% [Lui et al., 1993]. Thus we can conclude that in used approximation IWI can't provide necessary ion heating in current disruption during the substorm onset. However it could serve as a trigger for another type of instability, for example, the tiring-instability.

Nevertheless the investigation of IWI has preliminary character. The numerical value of k_m, the wave vector corresponding to maximum growth rate calculated from the linear theory, for the case of highest possible drift speed, k_m 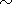2.8 10^-8 cm^-1 for the inner edge and k_m 1.9 10^-8 cm ^-1. The corresponding wavelengths have the same orders as the ion cyclotron radii which are of the order 3900 km for the inner edge and 8000 km for the midtail. Moreover these wavelengths increase with development of the instability. So we need to take into account the influence of the ambient magnetic field on the ion dynamics. In paper [Wu et al., 1992] it was shown that the linear theory is slightly different for the magnetized and unmagnetized ions. However the process of quasilinear relaxation for these cases may be drastically different. The characteristic length of magnetic field inhomogeneities in the Earth's magnetotail is of the order of the ion cyclotron radius so spatial magnetic field distribution must be taken into account. Analysis of IWI in the cold plasma approximation was done in [Yoon and Lui, 1996] for the Harris neutral sheet. However the authors didn't take into consideration any kinetic effects which can change the dispersion equation. The analysis of Galileo data has shown that in the vicinity of the neutral sheet the ions has non-maxwellian distribution [Burinskaya and Indenbom, 2000]. The problem of the excitation of such low-frequency electromagnetic waves on the non-maxwellian distribution and the question of their stability to such disturbances remains open.

Acknowledgments

References

Baumjohann, W., The near-Earth plasma sheet: An AMPTE/IRM perspective, Space Science Reviews, 64, 141, 1993.

Biskamp, D., R. Z. Sagdeev, and K. Schindler, Nonlinear evolution of the tearing instability in the geomagnetic tail, Cosmic Electrodynamics, 1, 297, 1970.

Burinskaya, T. M., and E. M. Indenbom, Excitation of Low-Frequency Electrostatic oscillation in a collisionless plasma with an anisotropic ion distribution, Plasma Phys. Rep., 26, 49, 2000.

Chang, C.-L., H. K. Wong, and C. S. Wu, Electromagnetic instabilities attributed to a cross-field ion drift, Phys. Rev. Lett., 65, 1104, 1990.

Davidson, R. C., D. A. Hammer, I. Haber, and C. E. Wagner, Nonlinear development of electromagnetic instabilities in anisotropic plasmas, Phys. Fluids, 15, 317, 1972.

Galeev, A. A., and R. Z. Sagdeev, Nonlinear plasma theory, in Rev. Plasma Phys., 7, edited by M. A. Leontovich, Atomizdat, Moscow, 1973.

Lui, A. T. Y., Current disruption in the Earth's magnetosphere: Observations and models, J. Geophys. Res., 101, 13,067, 1996.

Lui, A. T. Y., C.-L. Chang, A. Mankofsky, H.-K. Wong, and D. Winske, A cross field current instability for substorm expansion, J. Geophys. Res., 96, 11,389, 1991.

Lui A. T. Y., P. H. Yoon, and C.-L. Chang, Quasi-linear analysis of ion Weibel instability in the Earth's neutral sheet, J. Geophys. Res., 98, 153, 1993.

Shapiro, V. D., and V. I. Shevchenko, Quasilinear theory of instability of a plasma with an anisotropic ion velocity distribution, Sov. Phys. JETP, 18, 1109, 1964.

Weibel, E. S., Spontaneously growing transverse waves in a plasma due to an anisotropic velocity distribution, Phys. Rev. Let., 2, 83, 1959.

Wu, C. S., P. H. Yoon, L. F. Ziebell, C.-L. Chang, and H. K. Wong, A purely growing electromagnetic mode operative in the geomagnetic tail, J. Geophys. Res., 97, 141, 1992.

Yoon P. H., Plasma heating by a purely growing mode driven by cross-field currents in quasiperpendicular collisionless shock, Phys. Fluids B, 3, 3074, 1991.

Yoon, P. H., and A. T. Y. Lui, Nonlocal ion-Weibel instability in the geomagnetic tail, J. Geophys. Res., 101, 4899, 1996.

Yoon, P. H., C. S. Wu, and M. E. Mandt, Ion heating by kinetic cross-field instability due to reflected ions at quasiperpendicular shock, Phys. Fluids B, 4, 719, 1992.