 Received December 15, 1999
Received December 15, 1999N. A. Barkhatov
Nizhny Novgorod State Pedagogical University, Nizhny Novgorod, Russia
P. A. Bespalov
Institute of Applied Physics, Nizhny Novgorod, Russia
Complicated events with different characteristic scales taking place on the solar surface and in the interplanetary space initiate disturbance of wide spectrum inhomogeneities in the solar wind [Schmidt and Marsch, 1995]. The interplanetary medium parameters' fluctuations usually correspond to weak plasma turbulence and can be described in terms of wave turbulence [Chashey and Shishov, 1981]. Degree law of background wave turbulence spectrum [Denskat and Neubauer, 1982] may be the evidence of the non-linear turbulence scales cascade. Modern observational possibilities do not allow to define exactly which phenomenologic theory is true: Kolmogorov's [Kolmogorov, 1965] or Iroshnikov's theory [Iroshnikov, 1963]. More over, the dependence of turbulence spectrum shape on radial coordinate is attributed to the existence of the solar wind. The average background turbulence characteristics are considered to be well-known and are defined from observation [Readhead et al., 1978; Riley et al., 1996; Sari and Valley, 1976].
Conditions existing in the solar wind cause generation of comparatively stable magnetohydrodynamic (MHD) disturbances of various scales. Parametric decay of the solar wind Alfvén wave was studied thoroughly by Hollweg [1974] for small scale turbulence.
Solar wind Alfvén waves have rather weak collision and collisionless dampings. Therefore, when excited near the Sun, they bear the information on the solar wind far regions, which are not available for direct space observations. It is possible to define the corporal angle of source from which these waves could come in ultra Alfvénic flow. Some scientific schools have developed models of the evolution of the Alfvén wave power spectrum with solar distance [Goldstein et al., 1995; Marsch and Tu, 1996; [Zank et al., 1996]. A relatively recent review of the subject was given by Tu and Marsch, [1995]. To calculate MHD disturbance transport, it is necessary to take into consideration its modification as a result of interaction with the solar wind background turbulence. If the direct influence of MHD background turbulence is ignored, then it is possible to study wave parametric interaction against the background turbulence and to estimate the effective regular MHD wave attenuation caused by this process. However, it is necessary to take into account inhomogeneous medium peculiarities which become relevant within the long distances. They are: spherical solar wind, spiral interplanetary magnetic field and radial distribution of typical turbulence scales. It is also necessary to take into account the peculiarities of basic turbulence parameters' distribution.
This paper studies regular Alfvén wave attenuation caused by parametric interaction with background turbulence according to wave characteristic scales and the position of generation region in the solar wind. Attenuation as a result of such non-linear interaction between the given regular wave and the solar wind turbulence is compared with the findings obtained when studying the given wave dispersion on stationary inhomogeneities [Barkhatov and Belliustin, 1983]. Outcomes of numerical experiments and theoretical calculations [Kadomtsev, 1976] have shown, that Alfvén waves interact weakly. Therefore, of the entire hierarchy of three-wave processes, fast and slow magnetosound disturbances, which are effective sourses of Alfvén wave in the solar wind, are relevant. In this case some circumstances may result from that dispersing characteristics of Alfvén and fast magnetosound waves for small angles propagation to a magnetic field are close. Here it is possible to expect increase of interaction of Alfvén waves with large-scale fast magnetosound waves.
Of special interest to this research are two circumstances. At first, available experimental data do not allow immediately to measure Alfvén wave attenuation. For this purpose synchronous observations along the group trajectory are necessary in view of time delay and doppler of shifts on two spacecrafts. Secondly, the results obtained in the study allow to reveal the value of a large-scale turbulence as the reason of Alfvén wave attenuation. It should be mentioned, when it comes to problem of scattering, small-scale turbulence is considered.
We assume that Alfvén wave spectrum density Wk is not only geometrically developing along the beam, but also suffers the influence of the solar wind microstructure described in terms of wave turbulence. Both noted processes can be considered within the kinetic equation for waves [Kadomtsev, 1964]
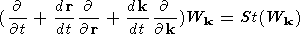 | (1) |
When the collisional term considered only three-wave process of wave interaction [Akhiezer, 1974] in random phase approximation, the right part of the equation (1) is the following
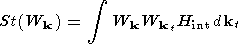 |
Here, W kt is the spectral density of turbulence energy, index kt corresponds the background turbulence, Hint is the Hamilton function of wave interaction.
Alfvén wave is regarded to have enough high energy density in comparison with turbulence background, therefore, energy pumping into it can be ignored. Then, in coordinate system connected with beam trajectory, equation (1) for stationary spectral density distribution W k can be also written down as
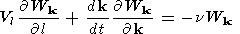 | (2) |
where Vl is the group velocity along the trajectory and n is the effective collision frequency which describe nonlinear interaction of regular Alfvén wave with background turbulence.
The integration of equation (2) is carried out in the Sun ecliptic plane along the beam trajectory for regular Alfvén waves with dispersion equations:
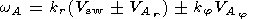 | (3) |
where signs
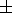 correspond to
Alfvén waves with wave vectors along and
against the interplanetary
magnetic field (IMF);
Vsw is a solar wind velocity;
VAr and
VA<FONT FACE='Symbol'>j
are components of Alfvén velocity.
The solution of equation (2) has the following form
correspond to
Alfvén waves with wave vectors along and
against the interplanetary
magnetic field (IMF);
Vsw is a solar wind velocity;
VAr and
VA<FONT FACE='Symbol'>j
are components of Alfvén velocity.
The solution of equation (2) has the following form
 |
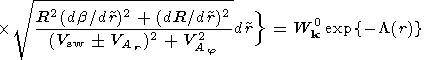 | (4) |
Here,
r, 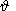 ,
j are spherical coordinates;
rs is a source coordinate;
b (r) = p
- arctan [r sin j/(rs
- r cos j)],
R = r2 + rs2 - 2 r
rs cos j ;
W k0 is the solution of uniform equation (1)
calculated
in geometric optics approximation for
n=0 and
,
j are spherical coordinates;
rs is a source coordinate;
b (r) = p
- arctan [r sin j/(rs
- r cos j)],
R = r2 + rs2 - 2 r
rs cos j ;
W k0 is the solution of uniform equation (1)
calculated
in geometric optics approximation for
n=0 and
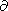 /
/ 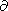 t = 0.
Note, that the geometrooptic wave vector evaluation in space is taken
into account in the design of
n ( r).
t = 0.
Note, that the geometrooptic wave vector evaluation in space is taken
into account in the design of
n ( r).
According to [Akhiezer, 1974; Barkhatov and Bespalov, 1988], regular Alfvén (index "A") wave nonlinearly interacting with fast magnetosound (index "F") and slow magnetosound (index "S") waves can be examined by the method used for waves' research in plasma physics. The principle of energy and impulse conservation, in case of wave interaction provides the conditions of synchronizing, under which integrals' expressions of collisions for three-waves interactions are written. Investigation of Alfvén wave attenuation take into account background turbulence invariability. This phenomenon can be defined as Alfvén wave parametric interaction. The probabilities of interaction in the system of MHD waves, one of which corresponds to the background turbulence, are included in the expression for effective collision frequency. This expression is written in cylindrical coordinate system with z axis, oriented along IMF B(r) = (Br2 + Bj2)1/2
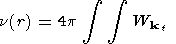 |
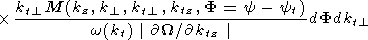 | (5) |
Here,
k has components
kz,
k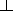 y and they are functions of
r and
y and they are functions of
r and
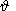 , defined by
geometric optics
, defined by
geometric optics
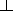 2
= k
2
= k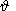 2 + (kr
sin a - kj
cos a)2
2 + (kr
sin a - kj
cos a)2
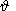 -1 (kr sin a - kj
cos a)
-1 (kr sin a - kj
cos a)
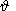 )
= Br (Br2 + Bj2)-1/2
)
= Br (Br2 + Bj2)-1/2
Component
ktz is evaluated taking into consideration
synchronizing conditions; formulas for
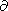 W /
W / 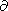 kt z are given
below;
M is proportional to the probability of
selected three-waves process.
kt z are given
below;
M is proportional to the probability of
selected three-waves process.
In (5), integral over the turbulence is taken in each point
r, 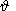 , j,
which is reached by regular Alfvén radiation
with dispersion equations (3) and
W k (r,
, j,
which is reached by regular Alfvén radiation
with dispersion equations (3) and
W k (r, 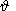 ,
j) spectrum,
obtained in geometric optic approximation.
The form of equation (1) characteristics,
when
,
j) spectrum,
obtained in geometric optic approximation.
The form of equation (1) characteristics,
when
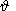 is fixed,
leads to simplification and, therefore,
n = n (r).
is fixed,
leads to simplification and, therefore,
n = n (r).
The processes which give irrevocable losses of Alfvén
waves are
the following:
A + Ft  F, A + St
F, A + St  F, A
F, A  F + St,
A
F + St,
A  Ft
+ S, A + St
Ft
+ S, A + St  F.
For example, sinchronising conditions
w1( k1)
F.
For example, sinchronising conditions
w1( k1) 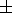 w2( k2)
- w3( k3) = 0,
( k1
w2( k2)
- w3( k3) = 0,
( k1 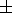 k2 -
k3 = 0 ) for waves with wave vectors along IMF are defined
by equations
k2 -
k3 = 0 ) for waves with wave vectors along IMF are defined
by equations
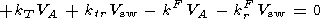 | (6) |
in which Vs is the sound velocity. Quite naturally, that weak attenuation of wave disturbances is necessary for realization of sinchronising conditions in form (6). Particulary for slow magnetosound, it occurs when the temperature of electron component largely exceeds the ionic one [Kadomtsev, 1964].
The comparison of levels of Alfvén wave
attenuation, which resulted
from different processes, is
presented below; it showed, that the most
significant process is
A + Ft  F process.
Its probability is as follows
F process.
Its probability is as follows
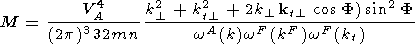 |
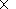 [kz ktz
+ k
[kz ktz
+ k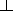 kt
kt 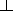 cos F
cos F
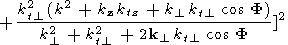 |
Here, n is the proton concentration; m is the proton mass; wA (k), wF (kF), wF (kt) are dispersion equations for interacting waves.
The results of attenuation coefficient calculation (4) are largely defined by turbulence spectrum in the solar wind. Turbulence energy spectral density W kT is determined on the basis of direct observation results, which have been summarized in Sari and Valley [1976], and experimental findings of Readhead et al. [1978]. The findings obtained on space craft Ulysses [Riley et al., 1996] should be taken into account. Assuming, that medium inhomogeneities are basically caused by magnetosound waves, magnetic field inhomogeneities' spectrums for fast and slow magnetosound turbulence will take the correspondent form
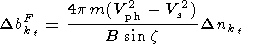 |
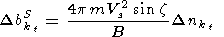 | (7) |
where z is the angle between kt and B ; Vph is the magnetosound wave phase velocity.
As a background turbulence model, choose the turbulence with isotropical angle spectrum and with one characteristic scale of disturbance a(r). Batchellor turbulence corresponds to these conditions [Batchelor, 1960]. Its spectral energy density takes the form
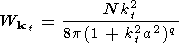 | (8) |
Coefficient a is determined as a function of distance to the Sun, taking into consideration the above mentioned experimental data. On this basis, spectrum of concentrational inhomogeneities was obtained
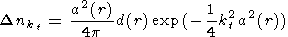 | (9) |
where
d(r) = 2.73  10-3
(r/1.5
10-3
(r/1.5  1013)-4,
and characteristic turbulence scale increases with
a distance from the Sun:
1013)-4,
and characteristic turbulence scale increases with
a distance from the Sun:
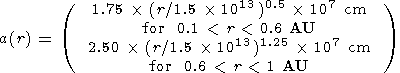 | (10) |
Here, AU is astronomical unit.
Coefficient value
q 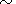 2.8
2.8 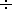 2.9 is calculated on the basis
of data about spectral turbulence
energy density
[Sari and Valley, 1976].
2.9 is calculated on the basis
of data about spectral turbulence
energy density
[Sari and Valley, 1976].
If the turbulence is generated only by fast or slow magnetosound waves, then by order of quantity
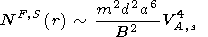 | (11) |
Thus, for
ka 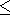 1 spectral density for a turbulence
of
fast and slow magnetosound waves is determined by the formula (8),
close to degree relation with parameters (10) and (11).
1 spectral density for a turbulence
of
fast and slow magnetosound waves is determined by the formula (8),
close to degree relation with parameters (10) and (11).
At ka > 1 according to expression (9) spectral density of energy has an exponential blockage. The selected model of turbulence spectrum does not contradict the recent experimental research [Bavassano, 1994].
The using of these expressions allow us to evaluate the maximum coefficient of relative Alfvén wave attenuation in the solar wind, namely L(r,k) - factor in expression (4).
Relative effective attenuation of regular Alfvén wave is analyzed. Let's consider the Alfvén waves with wave vectors k, which have components along the interplanetary magnetic field.
The expressions of effective collision frequency of the three-waves
processes are calculated, taking into account equations
(5)-(11).
For the
cases of small scale turbulence (SST) in comparison with
Alfvén wave scale
kt 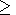 ko
ko
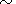 a-1
a-1 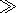 k (index ss) and large scale
turbulence (LST)
kt
k (index ss) and large scale
turbulence (LST)
kt 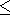 ko
ko
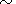 a-1
a-1 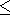 k (index ls),
the following expressions, correct to order of quantity,
were obtained
k (index ls),
the following expressions, correct to order of quantity,
were obtained
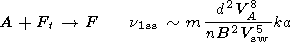 |
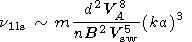 |
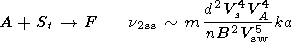 |
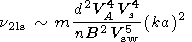 |
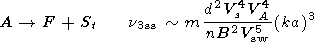 |
 |
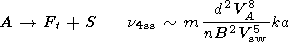 |
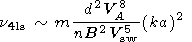 |
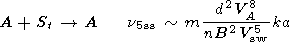 |
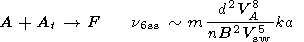 |
Here,
d is a coefficient of concentrate changing,
VA, Vs, Vsw,
n, B, d, a, k are the distance functions.
The medium and the small scale turbulence conditions within the whole
examined interval from
rs till
r = 1 AU.
are accomplishing for regular wave with wave number
k (r = rs) 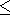 4
4 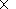 10-8 cm
-1 (for Alfvén wave with frequency
wA < 1.5 s-1 )
and large scale conditions
for
k(r = rs)
10-8 cm
-1 (for Alfvén wave with frequency
wA < 1.5 s-1 )
and large scale conditions
for
k(r = rs) 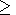 10-7 cm
-1 ( wA > 1.5 s
-1 ).
10-7 cm
-1 ( wA > 1.5 s
-1 ).
 Estimations of
n quantities for average values
of the solar wind parameters show the importance of
A + Ft
Estimations of
n quantities for average values
of the solar wind parameters show the importance of
A + Ft  F process providing the regular Alfvén
wave energy pumping into the fast magnetic sound.
In Figure 1
there are given results of numerical calculation of the
factor
L in expression (4) characterizing Alfvén wave
relative dumping as a result of confluence with fast magnetosound
turbulence. The factor
L is presented as a
dependence on
kA wave vector value of regular
wave,
when
r = rs.
The distance being counted from Earth orbit to the
region, where Alfvén disturbance was given,
is taken
as a parameter in
astronomic units in Figure 1.
F process providing the regular Alfvén
wave energy pumping into the fast magnetic sound.
In Figure 1
there are given results of numerical calculation of the
factor
L in expression (4) characterizing Alfvén wave
relative dumping as a result of confluence with fast magnetosound
turbulence. The factor
L is presented as a
dependence on
kA wave vector value of regular
wave,
when
r = rs.
The distance being counted from Earth orbit to the
region, where Alfvén disturbance was given,
is taken
as a parameter in
astronomic units in Figure 1.
Figure 1 indicates the effectiveness increase of this kind of parametric Alfvén wave scattering with their length reducing. The efficiency of energy pumping is decreasing with the distance from the Sun. This is explained by features of parameters' distribution of interplanetary medium and magnetic field along the trajectory. The results allow to define spheric layers of the near solar space responsible for Alfvén waves of different scales registered in the Earth's vicinity.
Analysis of parametrical interaction of the regular Alfvén wave along the trajectory with fast magnetosound turbulence has shown that Alfvén wave package attenuation takes place in the beginning of the way from the solar vicinity. The rate of energy pumping decreases with distance from the Sun. This can be attributed to the distribution peculiarities of interplanetary medium parameters and magnetic field along the trajectory. Alfvén wave attenuation due to energy pumping into fast magnetosound wave is most effective on large scale turbulence (LST) (Figure 1).
The role of small scale turbulence (SST) when compared to regular wave length turns to be significant for parametric interaction of given Alfvén wave with slow magnetosound and Alfvén waves in presence of fast magnetosound and slow magnetosound turbulences, respectively. In spite of turbulence characteristic scales growth, when distance to the Sun increases, the analyzed processes attenuate because of the general changing of plasma parameters and magnetic field.
Comparison of extinction obtained here with that calculated in Dobrowolny and Torricelly-Ciamponi [1985] Alfvén wave dissipation due to linear Landau attenuation in the solar wind shows the predominance of the parametrical effect.
Turbulence model in form of Batchelor turbulence used above
can be
used only for estimation of the process effectiveness,
as it was showed before, the turbulence spectrum in the
solar wind is
likely to have degree character. This means, that it is not obligatory
to investigate the case of middle scale turbulence
k 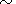 kt
kt 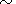 a-1. Such proportions are related to resonance of regular
wave
scattering
[Ishimaru, 1978].
However, in this case resonance
scattering contribution to the attenuation is, perhaps, less than from
large scale turbulence because of degree spectrum drop.
a-1. Such proportions are related to resonance of regular
wave
scattering
[Ishimaru, 1978].
However, in this case resonance
scattering contribution to the attenuation is, perhaps, less than from
large scale turbulence because of degree spectrum drop.
There is an intimate connection between the problem of non-linear interaction of the waves in plasma and wave transformation as a result of scattering by rather small chaotic inhomogeneities [Ginzburg, 1967]. Indeed, the obtained results of parametric wave interaction correspond to our findings concerning the wave scattering by the stationary inhomogeneities.
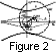 For interpretation of MHD waves' scattering mechanism and
quality
explanation of obtained results it is helpful to use geometric
relationships in
k space: comparison of space spectrum
surfaces of wave vectors of inhomogeneities scattering the waves
[Barkhatov and Belliustin, 1983].
The results obtained above can be explained by wave vector's surfaces
for MHD waves presented in Figure 2.
Wave vector surfaces of slow
magnetosound and Alfvén waves
are not close.
It is attributed to plasma resonances.
Reradiation by inhomogeneities as the
sources of these waves will be
the more considerable, the less
their space scales and, consequently,
the broader their wave vectors' spectrum are.
Reradiation of these inhomogeneities in
fast magnetosound wave is too
small and not connected with
plasma resonance.
It doesn't depend
on inhomogeneities' dimensions, when they are
smaller than the wave length (SST).
In Figure 2
arrows show the wave vectors of given regular Alfvén
waves.
The regions, occupied with wave vectors of scattering
turbulence
inhomogeneities
for cases of SST and LST, respectively, are depicted
with dotted and point-circular lines.
For cases studied above, when the given
Alfvén wave vector is parallel
to IMF direction, the total power
scattered in slow magnetosound and
Alfvén wave turns to be less
than the power radiated in fast
magnetosound wave by LST inhomogeneity.
This takes place in spite of the fact,
that space spectrums of SST
inhomogeneities cover large
regions and have resonance radiation
directions.
Of cause, the scattering picture is
enriched because of
participation of the
near wave vector surfaces in this process.
For interpretation of MHD waves' scattering mechanism and
quality
explanation of obtained results it is helpful to use geometric
relationships in
k space: comparison of space spectrum
surfaces of wave vectors of inhomogeneities scattering the waves
[Barkhatov and Belliustin, 1983].
The results obtained above can be explained by wave vector's surfaces
for MHD waves presented in Figure 2.
Wave vector surfaces of slow
magnetosound and Alfvén waves
are not close.
It is attributed to plasma resonances.
Reradiation by inhomogeneities as the
sources of these waves will be
the more considerable, the less
their space scales and, consequently,
the broader their wave vectors' spectrum are.
Reradiation of these inhomogeneities in
fast magnetosound wave is too
small and not connected with
plasma resonance.
It doesn't depend
on inhomogeneities' dimensions, when they are
smaller than the wave length (SST).
In Figure 2
arrows show the wave vectors of given regular Alfvén
waves.
The regions, occupied with wave vectors of scattering
turbulence
inhomogeneities
for cases of SST and LST, respectively, are depicted
with dotted and point-circular lines.
For cases studied above, when the given
Alfvén wave vector is parallel
to IMF direction, the total power
scattered in slow magnetosound and
Alfvén wave turns to be less
than the power radiated in fast
magnetosound wave by LST inhomogeneity.
This takes place in spite of the fact,
that space spectrums of SST
inhomogeneities cover large
regions and have resonance radiation
directions.
Of cause, the scattering picture is
enriched because of
participation of the
near wave vector surfaces in this process.
Thus, the connection between the problem of nonlinear interaction of waves in plasma and the question of wave transformation as a result of their scattering by stationary chaotic inhomogeneities is confirmed.
In this paper parametric interaction processes of Alfvén waves with different types of waves against the solar wind wave turbulence background were studied within the kinetic equation for wave spectral energy density in inhomogeneous medium. Special attention is paid to Alfvén wave attenuation with wave vectors near interplanetary magnetic field direction. Principal efficiency of three-wave processes for this wave group is explained by closeness of their dispersive characteristic to fast magnetosound wave dispersive characteristic. Here, the parameter distribution of interplanetary medium along wave transport trajectory was taken into account.
1. Alfvén wave attenuation was determined. Wave vector along IMF Alfvén wave attenuation resulting from energy pumping into fast magnetosound waves is most effective on large scale disturbance. Effectiveness of this process decreases with distance from the Sun.
2. Conclusions were made about the growth of Alfvén wave attenuation with increase of their length. This allows to define spherical layers of near solar space, which may be responsible for Alfvén wave of different scales, registred in the Earth vicinity. Deep corona layers are responsible for admitted Alfvén waves of large scales; external layers - for waves of small scales. That is why experimentally registered growth of turbulence scales with distance to the Sun doesn't seem to be strange.
3. It was noted, that the role of small scale turbulence in comparison to the length of regular wave, turns out to be relevant for parametrical interaction of given Alfvén wave with slow magnetosound and Alfvén wave. These processes occur in presence of fast and slow magnetosound turbulence, respectively. The scattering of given Alfvén wave scattering into fast magnetosound wave is small.
4. The obtained results correspond qualitatively to regular Alfvén wave scattering by moving stationary inhomogeneities observed before [Barkhatov and Belliustin, 1983]. This confirms the close connection of the problem of non-linear interaction of waves in plasma with the question of wave transformation as a result of their scattering by stationary chaotic inhomogeneities.
Akhiezer, A. I., Plasma Electrodynamic, Nauka, Moscow, 1974 (in Russian).
Barkhatov, N. A., and N. S. Belliustin, Resonance scattering of Alfvén waves in the solar wind, Radiophysics and Quantum electronics, 26, 385, 1983.
Barkhatov, N. A., and P. A. Bespalov, Evolution of Alfvén wave spectra in the solar wind, Radiophysics and Quantum electronics, 31, 133, 1988.
Batchelor, G. K., The theory of homogeneous turbulence, Cambridge, Univ. Press, 1960.
Bavassano, B., Recent observations of MHD fluctuations in the solar wind, Annales Geophysicae, 12, 97, 1994.
Chashey, I. V., and V. I. Shishov, Magnetohydrodynamic wave scattering on the solar wind turbulence, Geomagn. Aeron., 21, 961, 1981 (in Russian).
Denskat, K. U., and F. M. Neubauer, Statistical properties of low-frequency magnetic turbulence in the solar wind from 0.29 to 1.0 AU during the solar minimum conditions: Helios 1 and Helios 2, J. Geophys. Res., 87, 2215, 1982.
Dobrowolny, M., and G. Torricelly-Ciamponi, Alfvén wave dissipation in the solar wind, Astron. Astrophys., 142, 404, 1985.
Ginzburg, V. L., Electromagnetic wave propagation in plasma, Nauka, Moscow, 1967 (in Russian).
Goldstein, M. L., D. A. Roberts, and W. H. Matthaeus, Magnetohydrodynamic Turbulence in the Solar Wind, Ann. Rev. Astr. Astrophys., 33, 283, 1995.
Hollweg, J. V., Hydromagnetic waves in interplanetary space. Astr. Soc. Pacific., 86, 561, 1974.
Iroshnikov, R. S., On conductive liquid turbulence in strong magnetic field, Astron. J., 40, 742, 1963.
Ishimaru, A., Multiple Scattering, Turbulence, Rough Surfaces and Remote Sensing, Vol. 2, Academic Press, New York, 1978.
Kadomtsev, B. B., Plasma turbulence, in Theory plasma questions, 4, 188, Atomizdat, Moscow, 1964 (in Russian).
Kadomtsev, B. B., Collective Events in Plasma, Nauka, Moscow, 1976 (in Russian).
Kolmogorov, A. N., Local structure of turbulence in noncompressionality viscosity liquid when are very large Reynolds numbers, Dokl. Akad. Nauk, 30, 1385, 1965 (in Russian).
Marsch, E., and C.-Y. Tu, Spatial evolution of the magnetic spectral exponent in the solar wind Helios and Ulysses comparison, J. Geophys. Res., 101, 11,149, 1996.
Readhead, A. C. S., M. C. Kemp, and A. Hewish, The spectrum of small-scale density fluctuations in the solar wind, Monthly Notices Res. Astr. Soc., 185, 207, 1978.
Riley Pete, C. P. Sonett, B. T. Tsurutani, A. Balogh, R. J. Forsyth, and G. W. Hoogeveen, The properties of arc polarized Alfvén Waves in the ecliptic plane: Ulysis observations, J. Geophys. Res., 101, 19,987, 1996.
Sari, J. W., and G. C. Valley, Interplanetary magnetic field power spectra: mean field radial or perpendicular to radial, J. Geophys. Res., 81, 5489, 1976.
Schmidt, J. N., and E. Marsch, Spatial transport and spectral transfer of solar wind turbulence composed of Alfvén waves and convective structures: 1. The theoretical model, Annales Geophysicae, 12, 459, 1995.
Tu, C.-Y., and E. Marsch, MHD structures, waves and turbulence in the solar wind: Observations and theories, Space Sci. Rev., 73, 1, 1995.
Zank, G. P., C. W. Smith, and W. H. Matthaeus, Evolution of turbulent magnetic fluctuation power with heliospheric distance, J. Geophys. Res., 101, 17,093, 1996.
 |