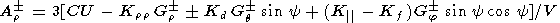
M. V. Alania
Geophysical Institute, Tbilisi, Georgia
T. V. Bochorishvili and K. Iskra
Institute of Physics and Mathematics, Sedlse, Poland
Received December 15, 1999
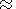 46o)
between the interplanetary magnetic field lines and Sun-Earth line,
the solar wind velocity
U (
46o)
between the interplanetary magnetic field lines and Sun-Earth line,
the solar wind velocity
U ( 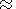 420 km s-1 ),
the ratio between the
cross-field ( K
420 km s-1 ),
the ratio between the
cross-field ( K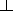 ) and field-aligned
( K
) and field-aligned
( K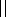 ) diffusion
coefficients,
K
) diffusion
coefficients,
K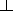 /K
/K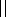 = a (
= a (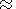 0.33), and
other parameters characterizing modulation of galactic cosmic rays
in the interplanetary space.
0.33), and
other parameters characterizing modulation of galactic cosmic rays
in the interplanetary space.
The effect of the sector structure of the interplanetary magnetic field (IMF) on the galactic cosmic ray (GCR) anisotropy is of a great interest. On the one hand, it allows us to solve the problem of the effect of particle drift on the GCR anisotropy, which still remains important. On the other hand, when the effect of particle drift on the anisotropy is determined rather reliably, we can develop a set of algebraic equations involving the spatial components of the GCR anisotropy derived from experimental data. This set of equations may be consequently used to calculate the components of the tensor of the GCR anisotropic diffusion and the solar wind parameters. According to Alania et al. [1983, 1987] and Riker and Ahluwalia [1987], the set of equations for the GCR anisotropy components is
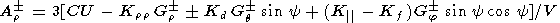 | (1) |
 | (2) |
 | (3) |
Here
Kd,
Kf, and
K| are the drift diffusion
coefficient and cross-field and field-aligned (relative to the IMF
lines) diffusion coefficients of GCR, respectively;
Gr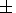 ,
Gq
,
Gq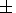 , and
Gj
, and
Gj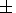 are the radial,
heliolatitudinal, and azimuth gradients of the GCR in the
interplanetary space,
y is the angle between the IMF lines and
the Sun-Earth line,
U and
V are the velocities of the solar wind
and GCR particles, respectively, and
C is the Compton-Getting
effect ( C
are the radial,
heliolatitudinal, and azimuth gradients of the GCR in the
interplanetary space,
y is the angle between the IMF lines and
the Sun-Earth line,
U and
V are the velocities of the solar wind
and GCR particles, respectively, and
C is the Compton-Getting
effect ( C 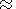 1.5 for the GCR particle energy detected
by the
neutron monitors). As (1)-(3) demonstrate, the GCR anisotropy
(detected by the neutron monitors at the Earth's surface) is caused
mainly by diffusion, convection, and drift of GCR particles in the
regular IMF. On the average, it is 0.3-0.4%.
Alania et al. [1983, 1987]
have shown that in this case the
particle drift contribution can amount to 15-20% of the mean
anisotropy. We should distinguish two types of the drift effect on
the GCR anisotropy. The first one caused by the
gradient and
curvature of the global IMF can be derived from the measurements of
the mean diurnal GCR variation in different solar cycles,
qA>0 and
qA<0 (when
qA>0,
the IMF lines exit from the northern solar
hemisphere, and when
qA<0, they enter the northern solar
hemisphere). The second drift type caused by the existence of local
spatial
gradients of the GCR manifests itself in different sectors
of the IMF. However, whereas the drift of the first type can be
derived from the GCR anisotropy merely by averaging the data over a
long period (for instance, 11 years), it is difficult to
unambiguously reveal the drift effect of the second type because of
considerable variations in the solar wind parameters during short
periods comparable with durations of the positive and negative
sectors of the IMF.
1.5 for the GCR particle energy detected
by the
neutron monitors). As (1)-(3) demonstrate, the GCR anisotropy
(detected by the neutron monitors at the Earth's surface) is caused
mainly by diffusion, convection, and drift of GCR particles in the
regular IMF. On the average, it is 0.3-0.4%.
Alania et al. [1983, 1987]
have shown that in this case the
particle drift contribution can amount to 15-20% of the mean
anisotropy. We should distinguish two types of the drift effect on
the GCR anisotropy. The first one caused by the
gradient and
curvature of the global IMF can be derived from the measurements of
the mean diurnal GCR variation in different solar cycles,
qA>0 and
qA<0 (when
qA>0,
the IMF lines exit from the northern solar
hemisphere, and when
qA<0, they enter the northern solar
hemisphere). The second drift type caused by the existence of local
spatial
gradients of the GCR manifests itself in different sectors
of the IMF. However, whereas the drift of the first type can be
derived from the GCR anisotropy merely by averaging the data over a
long period (for instance, 11 years), it is difficult to
unambiguously reveal the drift effect of the second type because of
considerable variations in the solar wind parameters during short
periods comparable with durations of the positive and negative
sectors of the IMF.
The goal of this paper is to reveal the effect
of the drift of the
second type on the GCR anisotropy in different positive and
negative sectors of the IMF and to calculate the solar wind
velocity, components of the anisotropic diffusion tensor, and other
GCR modulation characteristics by using (1)-(3). The most
important parameter is the
K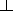 /K
/K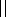 ratio
(K
ratio
(K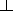 /K
/K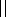 = a).
It demonstrates the character
of variations in the IMF irregularity and determines the role of
the GCR particle drift in the heliosphere.
Alania et al. [1983]
have analyzed the set of equations (1)-(3) assuming
that the GCR gradients in the opposite IMF sectors are equal to
each other. In order to determine the anisotropy components
Ar
= a).
It demonstrates the character
of variations in the IMF irregularity and determines the role of
the GCR particle drift in the heliosphere.
Alania et al. [1983]
have analyzed the set of equations (1)-(3) assuming
that the GCR gradients in the opposite IMF sectors are equal to
each other. In order to determine the anisotropy components
Ar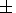 and
Aj
and
Aj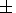 ,
the method of harmonic analysis
was applied. A similar work without specific calculations has been
recently performed by
Ahluwalia and Dorman [1997].
In this
work the effect of the drift on the GCR anisotropy was deduced from
the data for the period of the solar minimum in 1976. It is known
that during the periods of solar minimum the IMF sector structure
is rather pronounced. However, not only the short-period variations
in the solar wind parameters and GCR intensity, but also the
variations related with the Sun rotation period are weak
[Alania et al., 1983; 1987].
Contrary to our previous papers,
here we use the global survey method for determination of the
Ar,
Aq, and
Aj spatial components of the
GCR
anisotropy
[Belov et al., 1995].
Moreover, the calculations
were performed for the positive and negative sectors no shorter
than 4 days. The latter condition is a rigorous criterion for the
data selection and reduces the amount of statistical material.
However, in this case the effect of a certain sector of the IMF on
particle travel can be revealed more reliably, that is, the GCR
particle drift in the regular IMF can be determined relatively
reliably. While averaging the data over a period much longer than
the Sun rotation period, we may assume that the heliolongitudinal
gradient is zero
(Gj
,
the method of harmonic analysis
was applied. A similar work without specific calculations has been
recently performed by
Ahluwalia and Dorman [1997].
In this
work the effect of the drift on the GCR anisotropy was deduced from
the data for the period of the solar minimum in 1976. It is known
that during the periods of solar minimum the IMF sector structure
is rather pronounced. However, not only the short-period variations
in the solar wind parameters and GCR intensity, but also the
variations related with the Sun rotation period are weak
[Alania et al., 1983; 1987].
Contrary to our previous papers,
here we use the global survey method for determination of the
Ar,
Aq, and
Aj spatial components of the
GCR
anisotropy
[Belov et al., 1995].
Moreover, the calculations
were performed for the positive and negative sectors no shorter
than 4 days. The latter condition is a rigorous criterion for the
data selection and reduces the amount of statistical material.
However, in this case the effect of a certain sector of the IMF on
particle travel can be revealed more reliably, that is, the GCR
particle drift in the regular IMF can be determined relatively
reliably. While averaging the data over a period much longer than
the Sun rotation period, we may assume that the heliolongitudinal
gradient is zero
(Gj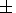 = 0).
Taking into account that
Gj
= 0).
Taking into account that
Gj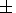 = 0 and performing a simple transformation, we
obtain, instead of (1)-(3), the following set of equations:
= 0 and performing a simple transformation, we
obtain, instead of (1)-(3), the following set of equations:
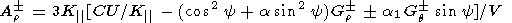 | (4) |
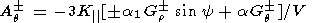 | (5) |
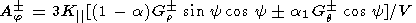 | (6) |
Here
a and
a1 are the ratios between the cross-field
Kf and drift
Kd diffusion coefficients to the
field-aligned diffusion coefficient
K|,
respectively
(K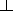 /K| = a, Kd/K| =
a1). Now the
set of equations (4)-(6) takes the form:
/K| = a, Kd/K| =
a1). Now the
set of equations (4)-(6) takes the form:
 | (7) |
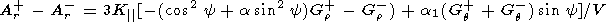 | (8) |
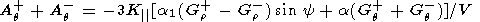 | (9) |
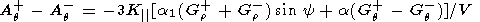 | (10) |
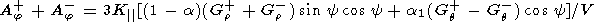 | (11) |
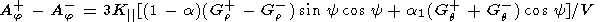 | (12) |
where Gr+, Gr-, Gq+, and Gq- are the radial and heliolongitudinal gradients of GCR in different IMF sectors.
The anisotropy components Ar+, Ar-, Aq+, Aq-, Aj+, and Aj- were found by using the data from the neutron monitors of the worldwide network of stations for the period of solar minimum (1976). The data for the IMF polarity were taken from Zaitsev [1984]. The neutron monitors (especially those with the cutoff thresholds lower than 5 GV) were selected taking into account similar characters of changes in the diurnal variation in different IMF sectors, which was determined by the ordinary harmonic analysis. Table 1 lists the stations of neutron monitors used in the global survey analysis. It also presents the number of days used for the analysis of data for different IMF sectors at each station. These periods are different because, for some stations, the changes in the diurnal variation amplitudes higher than 0.7% were not considered. Hourly data from each station were averaged, and thus the average diurnal waves for each IMF sector for 1976 were obtained. Then the GCR anisotropy components Ar+, Ar-, Aq+, Aq-, Aj+, and Aj- were determined by the global survey method.
When using the obtained GCR anisotropy components Ar+, Ar-, Aq+, Aq-, Aj+, and Aj- to solve (7)-(12), one should take into account that, whereas the components Ar+, Ar-, Aj+, and Aj- can be determined rather reliably, there is an uncertainty in the Aq+ and Aq- components. This problem is connected with a possible north-south asymmetry of the GCR intensity and heliolatitudinal gradient. For a reliable determination of the northsouth asymmetry of the GCR intensity, special investigations using the solar activity data are required.
Therefore, only the Ar+, Ar-, Aj+, and Aj- components of the GCR anisotropy may be used when solving (7)-(12). However, in this case the number of unknowns exceeds the number of equations, and certain simplifications are required. Assume that the like GCR gradients in different IMF sectors equal each other, that is, Gr+ = Gr- and Gq+ = Gq-. In addition, we may also use equation (10) under the assumption that there is a north-south asymmetry of GCR which remains constant during a year, for instance, 1976. Then the set of equations (7)-(12) looks like
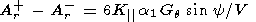 | (13) |
 | (14) |
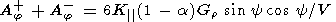 | (15) |
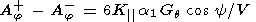 | (16) |
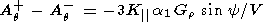 | (17) |
The global survey with the use of the data from the worldwide
network of neutron monitors gave the following results:
Ar+ = -0.20%,
Ar- = -0.11%,
Aj+ = -0.28%, and
Aj- =-0.19%.
Using (13) and (16) and the equation
Ref. 4/A
[Parker, 1965]
(where
W is the angular velocity of the Sun and
R0 is the Sun-Earth distance), we have estimated the angle between
the IMF lines and the Sun-Earth line to be
y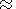 46o,
and
the solar wind velocity was found to be
U
46o,
and
the solar wind velocity was found to be
U 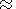 420 km s-1.
This
value is in good agreement with the average solar wind velocity at
the Earth's orbit,
U
420 km s-1.
This
value is in good agreement with the average solar wind velocity at
the Earth's orbit,
U 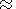 450 km s-1,
obtained by direct
measurements in the interplanetary space
[King, 1979].
Using the obtained
y and
U and equations (14) and (15), we have
calculated
a = K
450 km s-1,
obtained by direct
measurements in the interplanetary space
[King, 1979].
Using the obtained
y and
U and equations (14) and (15), we have
calculated
a = K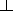 /K
/K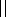
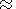 0.33
0.33
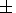 0.05 (the ratio between the cross-field and field-aligned
diffusion
coefficients of GCR). This value is 4-5 times higher than
a = 0.05-0.1 taken by various authors in numerical
solution of the
equation for the GCR anisotropic diffusion. The overestimation is
possibly due to the assumption that the spatial gradients in
different IMF sectors are equal, that is,
Gr+ = Gr-
and
Gq+ = Gq-.
We have also calculated the ratio
between the drift diffusion coefficient
Kd and the
field-aligned diffusion coefficient
K| a1
0.05 (the ratio between the cross-field and field-aligned
diffusion
coefficients of GCR). This value is 4-5 times higher than
a = 0.05-0.1 taken by various authors in numerical
solution of the
equation for the GCR anisotropic diffusion. The overestimation is
possibly due to the assumption that the spatial gradients in
different IMF sectors are equal, that is,
Gr+ = Gr-
and
Gq+ = Gq-.
We have also calculated the ratio
between the drift diffusion coefficient
Kd and the
field-aligned diffusion coefficient
K| a1 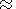 0.47
0.47 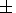 0.05,
the product of the field-aligned diffusion coefficient by the
radial GCR gradient
K| Gr = 7.2
0.05,
the product of the field-aligned diffusion coefficient by the
radial GCR gradient
K| Gr = 7.2 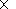 109 cm-1 % AU-1,
and the product of the field-aligned diffusion coefficient by
the heliolatitudinal gradient of GCR
K| Gq= 1.4
109 cm-1 % AU-1,
and the product of the field-aligned diffusion coefficient by
the heliolatitudinal gradient of GCR
K| Gq= 1.4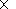 109 cm
2 s-1 % AU-1 (AU is the astronomic unit). If we
assume the average radial gradient to be
109 cm
2 s-1 % AU-1 (AU is the astronomic unit). If we
assume the average radial gradient to be
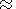 2% per AU, %%% ???
then
K
2% per AU, %%% ???
then
K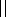 = 3.6
= 3.6 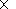 1022 cm2 s-1 and the heliolatitudinal
gradient is
Gq = 0.4% per AU. %%% ???
Unfortunately, the set of
equations (8)-(12) cannot be solved for
Gr+,
Gr-,
Gq+, and
Gq- because of the
lack of information
on absolute values of the anisotropy components
Aq+ and
Aq- due to uncertainty
of the north-south asymmetry of GCR
intensity.
1022 cm2 s-1 and the heliolatitudinal
gradient is
Gq = 0.4% per AU. %%% ???
Unfortunately, the set of
equations (8)-(12) cannot be solved for
Gr+,
Gr-,
Gq+, and
Gq- because of the
lack of information
on absolute values of the anisotropy components
Aq+ and
Aq- due to uncertainty
of the north-south asymmetry of GCR
intensity.
(1) Using the data from the global network of neutron monitors and
the global survey method, we have unambiguously determined the
effect of particle drift ( 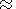 0.04-0.05%)
on both the azimuth
and radial components of the GCR anisotropy at the solar minimum
(1976). The magnitude of the GCR anisotropy vector in the positive
IMF sector is higher, and the phase is shifted toward earlier
hours.
0.04-0.05%)
on both the azimuth
and radial components of the GCR anisotropy at the solar minimum
(1976). The magnitude of the GCR anisotropy vector in the positive
IMF sector is higher, and the phase is shifted toward earlier
hours.
(2) Solving the set of algebraic equations derived by using the GCR
anisotropy spatial components for 1976, we have determined the
following quantities: the angle between the IMF lines and the
Sun-Earth line
y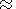 46o
;
the solar wind velocity
U
46o
;
the solar wind velocity
U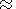 420 km s-1 (direct measurements in the interplanetary space
give the mean solar wind velocity at the Earth's orbit equal to
420 km s-1 (direct measurements in the interplanetary space
give the mean solar wind velocity at the Earth's orbit equal to
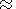 450 km s-1 );
the ratio between the cross-field
K
450 km s-1 );
the ratio between the cross-field
K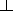 and
field-aligned
K
and
field-aligned
K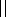 GCR diffusion coefficients
a
GCR diffusion coefficients
a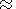 0.33
0.33 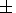 0.05 ;
the ratio between the drift
Kd and field-aligned
K| diffusion coefficients
a1
0.05 ;
the ratio between the drift
Kd and field-aligned
K| diffusion coefficients
a1 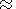 0.47
0.47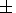 0.05.
0.05.
Ahluwalia, H. S., and L. I. Dorman, Computation of transverse cosmic ray particle density gradients, in Proceedings of the 25th International Cosmic Ray Conference, vol. 2, pp. 101-104, Durban, South Africa, 1997.
Alania, M. V., et al., The effect of the particle drift on cosmic ray anisotropy, in Proceedings of the 18th International Cosmic Ray Conference, vol. 10, pp. 91-94, Bangalore, India, 1983.
Alania, M. V., et al., Modulation of Galactic Cosmic Rays by the Solar Wind, edited by M. Kats, pp. 3-94, Metsniereba, Tbilisi, 1987 (in Russian).
Belov, A. V., E. A. Eroshenko, K. F. Yudakhin, and V. G. Yanke, Isotropic and anisotropic variations in cosmic rays in March-June, 1991, Izv. Akad. Nauk Ross. Ser. Fiz., 59 (4), 79, 1995 (in Russian).
King, J. H., Interplanetary Medium Data Book, Suppl. 1, World Data Center A, Greenbelt, Maryland, 1979.
Parker, E. N., The passage of energetic charged particles through interplanetary space, Planet. Space Sci., 13, 9, 1965.
Riker, J. F., and H. S. Ahluwalia, A survey of the cosmic ray diurnal variation during 1973-1979, II, Application of diffusion-convection model to diurnal anisotropy data, Space Sci., 35, 9, 1117, 1987.
Zaitsev, A. R., The interplanetary magnetic field polarity during 1957-1989. Mansurov's Catalogue, preprint 52 (526), IZMIRAN, 1984 (in Russian).