22 years and
T 5 years. Some
additional comments on the quasi-biennial variations of
P are
given.
Yu. R. Rivin
Institute of Terrestrial Magnetism, Ionosphere, and Radio Wave Propagation, Troitsk, Moscow Region, Russia
Received January 5, 1999
Ground-based and near-Earth measurements of the galactic cosmic
ray (GCR) flux show its significant modulation by the 11-year
cycle. This modulation has been still discovered in the beginning
of the 1950s
[Dorman, 1963],
however, the mechanism of its
generation is still obscure. It is believed to be related to the
complex and many-aspect impact of the solar wind and
irregularities of the interplanetary magnetic field "frozen"
therein on the galactic ray flux ( P )
[Chirkov, 1986;
Dorman, 1975;
Dorman et al., 1969].
On the basis
of the observations in three observatories, another interpretation
of the source is proposed hereafter. The interpretation takes into
account practical absence of any correlation between the
variations of the annual mean values of
P and solar wind dynamical
parameters (plasma velocity and density), and also different phase
shift between cycles of Wolf numbers
W and
P for even and odd
cycles of
W. In this analysis the data for large-scale solar
magnetic fields were used. Taking into account these fields and
discussing the results, we propose to use the cyclic variations of
the magnitude of the total solar magnetic field
B or
interplanetary magnetic field vector
B IMF as a
basis of the model of the cyclic variations of
P (instead of Wolf
numbers or other parameters of solar activity). The new
characteristic which was considered in particular by
Chirkov [1986]
and
Rivin and Obridko [1992]
not only
improves the correlation properties of the analytical model but,
taking into account the results of
Obridko and Rivin [1996],
provides a new approach to the problem of the
phase shifts of
P cycles relatively to cycles of
W and magnitudes
of the solar magnetic fields. Usage of the new characteristic
makes it possible also to suggest a new interpretation of the
P cyclicity with
T 22 years and
T 5 years. Some
additional comments on the quasi-biennial variations of
P are
given.
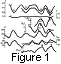Figure 1 shows the annual mean values of the GCR flux (number
of
pulses per hour) from the neutron monitor data of three American
observatories latitudinally spaced from the equator to high
latitudes
[NOAA, 1996].
Below in this figure, the
auxiliary data useful for analysis are also shown. These are the
variations of the annual mean values of the large-scale solar
magnetic field magnitudes observed by two different methods: as a
star field
Bs and directly on the photosphere surface
B (only the
radial component
BR in the near-equator zone is shown). Also
shown are
W and the
aa index of geomagnetic activity.
Bs,
W, and
aa index data are also available in Solar-Geophysical Data Prompt
Reports
[NOAA, 1996],]
and
BR data were presented by
Obridko and Rivin [1996]
where the cyclic variations of
BR and other components of
B were used for analysis
of temporal variations of the solar neutrino flux. Also
additionally used are the annual mean values of the interplanetary
medium parameters (Figure 1 shows only the solar wind velocity
V SW and
B IMF ) taken from
Rivin [1989]
and also calculated from the later data of King catalogue
available in the Internet. All the curves are smoothed by a
running three-year interval, and after that the smoothed curves
(cyclic variations) and, separately, quasi-biennial variations
obtained as differences of the initial and smoothed curves are
considered.
Now we will describe in more detail the additional data.
Obridko and Rivin [1996] discussed the 11-year variations in B and concluded that these are the result of a superposition of fields of two primary sources and in a first approximation may be described on the photosphere surface by the model:
 | (1) |
where
B0 0.5 Gs is the field
averaged over several cycles,
W = 2p/TW,
TW 22 years,
m is the
amplitude modulation depth,
Am 1.5 Gs,
w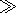
W
,
Tw < 1 year,
and
l is the phase shift between two
components (~8 months).
Obridko and Rivin [1996]
mentioned this shift but it was not included in the model there.
Later on the parameters of model (1) were specified and
developed ( Tw 27 days, the first and second terms
are the dipole and quadrupole fields, respectively), and the
mechanism of the 11-year cycle generation by these solar fields
was suggested
[Rivin, 1998a, b\link10].
The second term
in (1) is absent in the initial field
B if one uses annual means.
However for
B there appears an amplitude modulation of
this term which becomes determining in the 11-year cycle of
B. Thus the variations in
B are a sum of the
11-year cycles of the fields of two different origins, the field
of the second term in model (1) prevailing. It is assumed that the
temporal dipole variations in model (1) are described by
W and
partially
Bs , the variation of
BR describing mainly the quadrupole field dynamics. We
note that the
annual mean values of
W are only an index, that is, an indirect
characteristic of the behavior of the toroidal dipole magnetic
field (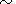 
103 Gs) on the photosphere.
Figure 1 shows that the cyclic variations of BR and Bs somewhat differ in phase (arrows) and, most important, in the ratio of maximum values in 21 and 22 cycles (the errors of each curves are less than ~10%). This difference seems to be associated with the different methods of obtaining of the two fields and therefore different dipole and quadrupole contributions in B. The main shortcoming of the Bs and BR series is their short length, but still they contain two cycles with different amplitude modulation and phase shifts which provides a minimum possibility for understanding of their difference.
The attracting of the aa index data is due to the possibility to use its long observation series for description of cyclic variations of V SW at scales longer than those the latter are known on. This possibility is based on the relation between variations of the annual means of geomagnetic activity and solar wind velocity. From literature the relation is known to be nearly linear. To illustrate this relation both curves are shown together in Figure 1 on the superposed interval.
Long time ago observations of the magnetic field of the Sun as a star were suggested as a method to obtain real-time information on variations of the interplanetary magnetic field (IMF). Nowadays (with accumulation of data on variation of B IMF from the satellite measurements during three cycles) there is a possibility to compare the coordination of the 11-year variations of the total solar magnetic field near the star and Earth surfaces, in particular for revealing their role in generation of the modulation of P.
Analysis of cyclic variations for the curves in Figure 1 leads to the following conclusions:
1) The cycles of P demonstrate a good antiphase correlation with the cycles of W and Bs. Their correlation with the cycles of BR is much weaker. The correlation of the cycles of P with Bs is higher than with W. It is because, first, in cycle 22 the increase of Bs exceeding the measurement error corresponds to considerable decrease of P, the fact agreeing with two curves being in antiphase, and, second, in the maximum of cycle 21 the curves P and Bs delay relative the maximum of W (arrows).
2) Despite the fact that, in some epochs, extreme of the aa index cycles coincide with the extreme of P cycles (1958, 1959, 1965, 1986, 1987), the geomagnetic activity cycles (particularly in the 1968-1983 interval) correlate with P cycles far worse than the W cycles do. This discrepancy can not be due to the errors of revealing of the V SW and aa index cycles.
3) The variations of
Bs and
B IMF occur
consistently (the linear correlation coefficient
r = 0.95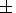 
0.06 ).
No phase shift between them is found.
The conclusion on the phase shifts between
P and solar activity
characteristics is of a principal importance for interpretation of
the source of the
GCR flux cycle. In this respect, the
phase diagrams of the cycles for part of the curves shown in
Figure 1
were
considered on the correlation plane separately for each of the
previous four cycles (see Figure 2). Their analysis leads to
the following conclusions:
1) The phase shift between the cycles of
P and
W depends on the
cycle number on Zurich scale: it is maximum (spreading of the
diagram) in odd cycles (the delay relative the phase of
W is
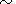2 years) and very small in even cycles.
2) The phase shifts between the cycles of P and aa index are determined less unambiguous; in the 20th-22nd cycles the geomagnetic activity is slightly ahead of P.
3) The variations of the annual mean values of V SW and aa index occur consistently, their relationship on each of three intervals on the correlation plane can be approximated by a linear regression equation.
4) The cycle of P lags from odd cycle of Bs by ~1 year and leads it by ~1 year in even cycle.
5) There is a following tendency. The phase of P is behind the phase of BR by ~1 year in odd cycles, whereas they coincide in even cycles.
It follows from Figure 2 that pronounced patterns in phase variations are only observed in the longest series (while comparing the phases of the P and W cycles). In our disposal there is no series of P and also Bs and B before 1954 in order to check the tendency of the phase shift from cycle to cycle obtained in Figure 2a. However one can refer to Dorman [1963] (see Figure 24.9 there) where similar phase diagrams to determine "some sort of hysteresis" were built from the initial data of m -meson intensity at the Huancayo observatory for cycles 18 and 19. In these diagrams the odd cycle diagram is spread more than the even cycle diagram, but the author paid no attention to this fact. The latter led to the fact that in the next figure in Dorman [1963] the displacement phase shift was determined from the initial curves for ~20 years. As a result, some average characteristic (3 months) strongly underestimated was obtained.
In addition, we analyzed the high-frequency part of smoothing
of
the
P and
W curves, which is largely associated with the
"quasi-biennial" variation (Figure 3). This figure compares the
P curves of the Calgary and Climax observatories having a nearly
similar magnetic rigidity threshold (~1-3 GeV) to show that
their antiphase variations began only since the second half of the
1980s. That means that in the Calgary observatory during most
part of the recording interval they were obviously due to the
registration noise. The magnetic rigidity for the curve of the
Huancayo observatory is much higher (~12 GeV), which results
in an abrupt decrease in the amplitude of these variations (and
the cyclic variations as well) and to a weakening of the
correlation. It is of primary importance that the quasi-biennial
variations of the GCR flux vary in antiphase with the same
variations of solar magnetic fields and have no phase shift
relative these fields (or it is not yet discovered at the data
discreteness available).
The results of the analysis presented above are related to two problems of description of GCR flux cyclic variations: 1) creation of an analytic model of these variation in which the cyclic variation of some solar parameter (rather often this is W ) is taken as a basis; and 2) discussion of possible mechanism of this variation generation.
Using annual values of W as a basis of an analytical model of cyclic variation of P, two main differences of curves are observed. First, the different amplitude modulation of the 11-year cycles: for example, in the recent two cycles (21 and 22) the W cycle magnitudes are almost equal, whereas the P cycle in cycle 22 demonstrates the flux decrease which is much stronger than in the previous cycle (Figure 1) and clearly exceeds the accuracy of P measurements. Second, the phase shift is usually averaged over a few cycles but depends (as it has been shown above) on parity of the W cycle number. The comparison of the curves P, Bs , and W shows that both differences disappear in a significant degree if one takes for modeling the curve of Bs cycles instead of W cycles. Such a substitution with a transition to cyclic variations of real solar magnetic fields located up to polar region latitudes improves significantly the quality and accuracy of the model. Moreover taking into account the results of Obridko and Rivin [1996], this substitution helps understanding that the problem of the shift of P cycles relative odd cycles of W is not a problem of the GCR flux. This is largely a problem of the dephasing of the magnetic fields of the dipole and quadrupole in (1). It should be noted that the small phase shifts in the diagram (Figure 2d) do not exclude a phase shift of the P cycle relative the Bs cycle which is much less than the shift relative the W cycle.
The necessity, modeling cyclic variations of P, to switch off from W to the magnitude of the total magnetic field of the Sun (or IMF) may be supported by the following: the W cycles describe in some approximation dynamics of only the toroidal component of the dipole magnetic field of the Sun, whereas variations of Bs describe dynamics of the poloidal component of the Bd dipole and Bq quadrupole. For the poloidal component the 11-year cycle amplitude of the quadrupole magnetic field on the photosphere surface is several times higher than that of the dipole. Above the photosphere (probably close to the surface of the source at ~2-3 Sun's radii) the relation between the Bq and Bd amplitudes is reversed, that fact being manifested in the amplitude variations of the magnetic field of the Sun as a star. At the same time, in the Bs cycles there still remains an input of Bq which leads to a phase shift relative the toroidal component of Bd (though one can not exclude that part of the shift is caused by the shift between the toroidal and poloidal components of the dipole field itself only). Our analysis shows that the cycle of P also has similar properties.
The change of the basis parameter of the analytical model of the P cyclic modulation should undoubtedly improve its quality. However one should state that unfortunately in the present time the data of large-scale solar magnetic field magnitude and IMF are limited only by two and three cycles, respectively. Therefore the conclusion made on this characteristics as an optimum basis of the analytic model should be still considered as preliminary.
The second problem for solution of which the results obtained may be used is determination of the origin of the P modulation. Dorman [1963] discussed a series of generation models of the GCR flux 11-year variation. Dorman et al. [1969] related the 11-year cyclicity of P to the corresponding variations of solar wind characteristics and interplanetary magnetic field irregularities. It was assumed that the variations of parameters of the interplanetary medium itself are determined by sunspot numbers over the entire disk or within particular latitudinal belt, coronal green line intensity, number of chromospheric flares et cetera. Such a view on the source of the 11-year GCR variation based on the Parker model is still widespread nowadays [Alaniya et al., 1995; Bazilevskaya et al., 1995].
The results of the analysis presented above show very weak (almost absent) correlation of the cyclic variations of P with the variations of the solar wind velocity and density and aa index of geomagnetic activity. This correlation is much less than with the variations of the solar dipole magnetic field which is manifested by W and Bs. Thus the cyclic variations of solar wind parameters (though they are possibly in some degree determined by solar magnetic fields) are significantly different than the GCR flux variations. This fact points to different sources of modulation of solar wind and GCR flux parameters by the 11-year cycle. It should be noted that we discuss here the modulation of P by the cyclic variation only. In another frequency range (for example, in case of the Forbush effect), the flux modulation mechanism of P by the Sun may be different and involve dynamical parameters of the solar wind. On the basis of the aforesaid one can suppose that the magnitude of the total solar magnetic field and its prolongation into the interplanetary space, IMF, are the main sources of the GCR flux modulation by the 11-year cycle. Why galactic cosmic ray flux is modulated by the magnitude but not the initial solar magnetic field itself, is an interesting question. But this question is a subject of another consideration.
The cycles with
T 11 years are strongest in variations
of
GCR flux annual values. The variation with
T 22 years is
more weak. A number of authors suggested a special role played by
the 22-year cyclicity in
P as compared with the 11-year cyclicity
[Stozhkov et al., 1986].
Belov et al. [1995]
noted that there is as yet no clear understanding of the Parker
modulation mechanisms in particular epochs of the 11-year cycle
and, most important for our study, no clear understanding of
sources of the 22-year cycle. Meanwhile the cause of 22-year
variation occurrence in the GCR flux is enough trivial for the
source indicated: the occurrence is probably a consequence of
detection of the main cycle of solar magnetic field with
T 22 years. As a result, in
Bs and
B IMF there appears the known modulation of the amplitude in
even-odd
11-year cycle pairs (in recent ~100 years the amplitude of
W even cycle was always higher than the amplitude of odd cycle).
Another obligatory result of the modulation of
P by the total
solar magnetic field magnitude (since the modulation is obviously
linear) is the existence, together with the second harmonic
(~11 years) of the main cycle also of the fourth harmonic
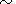( 5.5 years) with the amplitude approximately
5 times lower than the
amplitude of the second harmonic.
The quasi-biennial variation plays a special role in the modulation of P. The attention paid to this variation is much less than to the cycles with 11- and 22-year periods. However this variation is reliably revealed (see, for example, Okhlopkov et al. [1979]). The curves shown in Figure 3 confirm its existence and also demonstrate additional difficulties in its revealing, since in the observatories considered (and presumably in many other observatories) the amplitude of this variation is distorted by registration noises. In this paper we limit ourselves by this statement, avoiding more detailed study of the variation.
1) The cyclic variation of the galactic cosmic ray flux during recent ~40 years was caused by the flux modulation by the total solar magnetic field and its prolongation, interplanetary magnetic field. The dynamical parameters of the solar wind provide no input into generation mechanism of such variation of P.
2) The delay of the 11-year cycles of
P relative
W (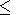 
1 year in
even cycles and ~2 years in odd cycles) is caused mainly by
properties of the modulation source itself but not the GCR flux
propagation time to the heliosphere boundary.
3) The existence in the GCR flux of ~22- and ~5-year waves with the amplitude much lower than the amplitude of the 11-year cycle is due to the detection of the initial total solar magnetic field, that is, the modulation is produced by the magnitudes Bs and B IMF.
4) Quasi-biennial variation of the GCR flux is detected at various monitors at various intervals with different accuracy. Approximately from the middle of the 1980s this variation is detected reliably in the Calgary and Climax observatories.
Alaniya, M. V., R. G. Aslamazashvili, G. K. Vanishvili, K. Iskra, and Z. Kobilinski, On mechanism of the 11-year cosmic ray variations and the solar wind large-scale structure, Izv. Akad. Nauk Rossia Ser. Fiz., 59 (4), 101, 1995.
Bazilevskaya, G. A., M. B. Kraynev, V. S. Makhmutov, A. K. Svirzhevskaya, N. S. Svirzhevskiy, and Yu. I. Stozhkov, Relationship between the galactic cosmic ray intensity and heliolatitudinal distribution of sunspots, Izv. Akad. Nauk Rossia Ser. Fiz., 59 (4), 75, 1995.
Belov, A. V., R. T. Gushchina, and I. V. Sirotina, Long-time modulation of the rigid spectrum of cosmic rays and its relationship with solar activity, Izv. Akad. Nauk Rossia Ser. Fiz., 59 (4), 71, 1995.
Chirkov, N. P., Variations of density of cosmic rays and the solar wind with solar activity cycle, in Cosmic Ray Modulation in the Solar System, edited by G. F. Krymskiy, pp. 3-14, Akad. Nauk SSSR, Yakutsk, 1986.
Dorman, L. I., Cosmic Ray Variations and Space Exploration, 1027 pp., Akad. Nauk SSSR, Moscow, 1963.
Dorman, L. I., Galactic Cosmic Ray Variations, 214 pp., Moscow State Univ., Moscow, 1975.
Dorman, I. V., L. I. Dorman, and L. I. Miroshnichenko, Investigation of the solar wind with the use of solar cosmic rays, in Problems of Space Physics, edited by S. K. Vsekhsvyatskiy, no. 4, pp. 3-12, Kiev State Univ., Kiev, 1969.
NOAA, Solar-Geophysics Data Prompt Reports, 1996.
Obridko, V. N., and Yu. R. Rivin, Magnetic field in the near-equatorial zone of the Sun, Astron. Zhurn., 73 (5), 812, 1996.
Okhlopkov, V. P., L. S. Okhlopkova, and T. N. Charakhch'yan, Quasi-biennial variations of cosmic rays, Izv. Akad. Nauk Rossia Ser. Fiz., 43 (4), 854, 1979.
Rivin, Yu. R., Cycles of the Earth and Sun, 165 pp., Nauka, Moscow, 1989.
Rivin, Yu. R., Specification of the analytical model of the magnetic field cyclic variation at middle and lower solar latitudes, Izv. Akad. Nauk Rossia Ser. Fiz., 62 (6), 1263, 1998a.
Rivin, Yu. R., Main elements of the generation mechanism of the cyclic variations of large-scale and local solar magnetic fields, Izv. Akad. Nauk Rossia Ser. Fiz., 62 (9), 1867, 1998b.
Rivin, Yu. R., and V. N. Obridko, Frequency composition of long-time variations of the magnetic field of the Sun as a star, Astron. Zhurn., 69 (5), 1083, 1992.
Stozhkov, Yu. I., N. K. Pereyaslova, and P. E. Pokrevskiy, A 22-year wave in the galactic cosmic ray flux, in Cosmic Ray Variations and Space Exploration, edited by L. I. Dorman, pp. 57-81, Inst. Terr. Magn. Ionos. Radio Wave Propagation, Moscow, 1986.