Submitted to
International Journal of Geomagnetism and Aeronomy
The energetics of the thermosphere-ionosphere system
within a solar activity cycle
M. A. Chernigovskaya
Institute of Solar-Terrestrial Physics, Irkutsk, Russia
Received January 25, 2000
Contents
Abstract
The global theoretical model of the dynamics and
electrodynamics of the ionosphere covering middle and low latitudes
was used to perform numerical calculations of the parameters
describing the energy state of the thermosphere-ionosphere system
(the Joule heating rate, kinetic energy of neutrals,
electromagnetic energy flux of large-scale electromagnetic fields)
under quiet geomagnetic conditions and to analyze their spatial and
temporal variations. The 1986-1996 time interval covering the 22nd
solar activity cycle was considered. The study revealed some
features of spatial, diurnal, seasonal and heliocyclic variations
in the energy characteristics caused by changes in the state of the
neutral atmosphere and ionosphere within a solar activity cycle.
1. Introduction
A central and most difficult problem in the physics of the Earth's
interplanetary environment is the problem of the energy balance in
the middle atmosphere-thermosphere-ionosphere-magnetosphere system.
This is especially true for lower thermosphere heights
(~140-250 km), since this region remains almost totally unexplored
owing to the lack of optical emissions measurements by ground-based
or spaceborne remote sensing, the difficulty in maintaining
satellite orbits due to the significant atmospheric drag, and the
power limitations in using lidar systems. Therefore information on
the dynamical and energetic characteristics associated with a
global electromagnetic field at lower thermosphere heights where
energy is intensively transferred between different spatial regions
of the atmosphere both through a global circulation and by wave
processes of different scales, is highly fragmentary and pertains
mainly to the auroral regions and the polar cap
[Killeen, 1987].
The midlatitude and low-latitude ionosphere, which
lies outside the area of direct action of powerful magnetospheric
sources, is therefore an object of subsequent scrutiny.
Zhovty and Chernigovskaya [1990],
Zhovty et al., [1997],
and
Chernigovskaya and Zhovty [1998]
described a diagnostic numerical model developed in the Institute
of Solar-Terrestrial Physics RAS under the supervision of late
Dr. E. I. Zhovty to study processes of global dynamics and
electrodynamics of the ionosphere at heights of the
E and
F regions. These processes include generation and evolution of
large-scale systems of neutral and charged particle motions,
formation of current systems, and processes of generation and
transport (propagation) of quasi-stationary electric fields. The
diagnostic model was used earlier in numerical calculations of the
Joule heating rate, kinetic energy of neutral particles, and
electromagnetic energy flux of the large-scale electromagnetic
field
[Chernigovskaya and Zhovty, 1998;
Zhovty et al., 1997]
for summer solstice conditions during the 21-st solar
cycle. We have revealed features of spatial, diurnal, seasonal and
heliocyclic variations of these characteristics caused by changes
in neutral atmosphere conditions within a solar activity cycle.
This paper is a further development of this analysis, and presents
calculations of the same energy characteristics for all seasons of
the 22-nd solar cycle.
2. Description of the Model
The model is aimed at self-consistent calculations (in terms of the
parameters described) of the large-scale velocity fields of the
neutral gas, ions, and electrons in a quasi-neutral
( N = ne 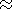 ni )
ionospheric plasma, and of the electric field and
current formed as a result of a given pressure gradient of the
neutral gas and an electric field applied from outside, the
distributions of atmospheric and ionospheric parameters at the
heights of
E and
F regions of the middle- and low-latitude
ionosphere under undisturbed geomagnetic conditions being known.
The geomagnetic field is
assumed to be a geocentric dipole field.
ni )
ionospheric plasma, and of the electric field and
current formed as a result of a given pressure gradient of the
neutral gas and an electric field applied from outside, the
distributions of atmospheric and ionospheric parameters at the
heights of
E and
F regions of the middle- and low-latitude
ionosphere under undisturbed geomagnetic conditions being known.
The geomagnetic field is
assumed to be a geocentric dipole field.
The system of model equations is solved in a three-dimensional
region having the shape of a spherical ring with the north boundary
at the colatitude
q0 = 25o and the
south boundary at
qm = 180o -
q0 = 155o.
The lower and upper
boundaries lie at the heights of
h0 = 90 km and
hm = 350 km above
the Earth's surface, respectively.
To describe the processes having
the horizontal scale of about the
Earth's radius
RE,
the vertical scale of about the scale height,
and the temporal scale of more than three hours, we use the
following system of equations
[Chernigovskaya and Zhovty, 1998;
Zhovty and Chernigovskaya, 1990;
Zhovty et al., 1997]:
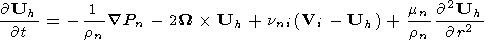 | (1) |
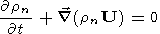 | (2) |
 | (3) |
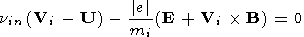 | (4) |
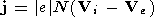 | (5) |
 | (6) |
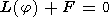 | (7) |
Here
U = (Ur, Uq,
Ul) is the neutral gas
velocity (wind);
Uh = (0, Uq,
Ul) is the
horizontal component of this velocity;
r is the radial distance
from the Earth's center;
q is the colatitude (counted from the
north pole);
l is the east longitude;
t is the time;
e,
i, and
n are the indices corresponding to electrons, ions and
neutrals, respectively;
Vk and
mk are the velocity and mass
of charged particles of the
k -th type, respectively;
N is the
charged particle density;
e is the electron charge;
rn,
Pn, and
mn are the density, pressure
and viscosity of
neutrals, respectively;
W
is the angular velocity of the
Earth rotation;
nks is the collision frequency
of particles of
k -th type with particles of
s -th type;
E and
j are the
strength and potential of the electric field;
j is the
electric current density; and
B is the induction of
geomagnetic field;
L(j) is an elliptical differential
operator; and
F is the source function. Equation (7) is obtained
from the condition of the electric current continuity. Its form
will be presented below.
The mathematical model was chosen with consideration of the
properties of the computer realization of numerical solution of
such equations
[Samarsky, 1971;
Samarsky and Nikolaev, 1978].
An additional condition, limiting a class of
solutions of the system of model equations (1)-(7), implies
considering the processes stationary in the coordinate system,
fixed relative to the Sun, with the longest time period of 24
hours. In this case there is a possibility of lowering the
dimension of the problem because all parameters depending on
W and
t are periodic functions of
(Wt+l).
Assuming
l to be fixed and using the relation
W 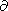 /
/ 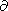 l =
l =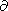 /
/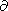 t, we
seek for the model solution in coordinates
(r, q, t).
t, we
seek for the model solution in coordinates
(r, q, t).
The effect of external (with respect to the region under
consideration) electric fields is taken into account by specifying
appropriate boundary conditions for the electric field potential
[Richmond et al., 1980].
Along with the condition of the time periodicity of the solution,
we specify the following additional conditions:
Uh = U0 jn
= 0 at h = h0
U = U0 at t = 0
 | (8) |
where
n is a normal to the lower boundary,
U0 is the solution
of equation (1) without taking into account the viscosity and
nonstationarity
[Zhovty et al., 1984], and
j1 is
the potential distribution specified at the high-latitude
boundaries
[Richmond et al., 1980].
In the analysis of the physical situation and numerical realization
of the mathematical model the form of the differential operator
describing spatial variations of the potential is important. The
anisotropy of the medium is responsible for the fact that the
differential operator
L(j) in equation (7) has the simplest
form in the coordinate systems related to the magnetic field
geometry
[Krylov and Shcherbakov, 1972;
Singh and Cole, 1987].
So the technique developed by
Gurevich and Tsedilina [1969],
Krylov and Shcherbakov [1972],
and
Richmond [1982] was used to obtain the following
equation (see, for example,
Zhovty and Chernigovskaya [1990]
and
Chernigovskaya and Zhovty [1998]) for
the zero-order (in respect to the small parameter equal to the
ratio of the transverse and field-aligned conductivities)
approximation of the electric field potential in a dipolar
coordinate system
(a, b, g) [Krinberg and Tashchilin, 1984]:
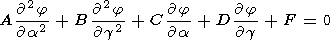 | (9) |
where
A,
B,
C, and
D are the functions dependent on the geometry,
boundary conditions and atmospheric gas parameters obtained by
integrating along magnetic field lines from a point with the
coordinate
b lying on the lower boundary of the region under
consideration, to a magneto-conjugate point
b*;
a and
g are coordinates in the plane normal to the magnetic
field;
and
F is the source function dependent on the above-mentioned
factors and on wind field distribution. In the coordinate system
(a, b, g), the boundaries of the two-dimensional
region in which the potential varies correspond to the values of
amin = 1 (equatorial boundary) and
amax = 5.7 (high-latitude boundary).
The region is a closed one in
g.
When deriving equation (9), it was also taken into account that
s0 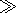 s1,
s2 (s0,
s1, and
s2 are the field-aligned, Pedersen,
and Hall conductivities,
respectively) and that there is no current across the lower
boundary (see equation (8)). The boundary condition for the
potential on the equatorial boundary
a = amin
= 1, as
well as on the high-latitude boundary
a = amax
= 5.7,
was defined from the observational data
[Richmond et al., 1980].
Then
s1,
s2 (s0,
s1, and
s2 are the field-aligned, Pedersen,
and Hall conductivities,
respectively) and that there is no current across the lower
boundary (see equation (8)). The boundary condition for the
potential on the equatorial boundary
a = amin
= 1, as
well as on the high-latitude boundary
a = amax
= 5.7,
was defined from the observational data
[Richmond et al., 1980].
Then
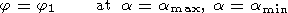 | (10) |
Thus the system of model equations (1)-(6), (9) with the boundary
conditions (8), (10), when specifying the transport coefficients,
the geomagnetic field, neutral atmospheric parameters and the
ionization distribution, is a closed one with respect to the
functions sought.
The Jacchia empirical model of neutral atmosphere parameters
[Jacchia, 1977]
used in the earlier calculations
[Chernigovskaya and Zhovty, 1998;
Zhovty and Chernigovskaya, 1990;
Zhovty et al., 1997]
is known to represent
insufficiently adequately the variations of atmospheric parameters
at lower thermosphere heights ( h < 110 km), because it assumes no
source associated with semidiurnal variations of neutral gas
parameters. This source can be represented by the tides generated
in the lower atmosphere as a result of the heating due to the
absorption of solar radiation energy by water and ozone, the tides
propagating to the thermosphere from below. In this case the tide
modes (2.2) and (2.4) dominate below 100 km and above 100-125 km,
respectively. The calculations of dynamic characteristics using the
neutral atmosphere model neglecting tides yield too low (compared
with experiment) values of the horizontal drift velocities and
hence too low potential electric field which they generate in the
dynamo region.
To eliminate this problem, in this version of the model of the
ionospheric dynamics and electrodynamics, the global distributions
of statistical parameters of the neutral atmosphere needed for
calculations were taken from the currently most comprehensive
atmosphere model MSIS 86 (also referred to as CIRA 86)
[Hedin, 1987].
Charged particle densities were taken according to
the
Ching and Chiu [1973]
model.
Input geophysical parameters of the numerical model are the number
of the day of the year, solar activity level (the solar radio flux
F10.7 at 10.7 cm wavelength in units of
10-22 W m
-2 Hz
-1, and
sunspot number
Rz ), and magnetic activity level (the
Ap index).
Furthermore, additional information is introduced to specify the
count mode.
3. Numerical Simulation Results
To analyze variations in energetics characteristics of the global
ionospheric system, numerical simulations were performed for quiet
geomagnetic conditions (the
Ap index was taken to be 4) for all
seasons of each year, from 1986 to 1996, which corresponds to the
22-nd cycle of solar activity. The calculations were carried out
for the days of the winter (December 22) and summer (June 22)
solstices, as well as for the days of the spring (March 21) and
autumn (September 23) equinoxes. The 22-nd cycle of solar activity
was characterized by a double maximum of activity (the main maximum
in 1989 with the sunspot number
Rz = 157.6, and the secondary
maximum in 1991 with
Rz = 145.7 ). The activity minima in 1986 and
1996 were characterized by
Rz = 13.4 and
Rz = 8.7, respectively.
Calculations were made of the kinetic energy of neutral particles
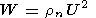 | (11) |
energy released due to the Joule dissipation of electric currents
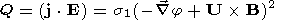 | (12) |
and Poynting's vector components of the electromagnetic energy flux
density
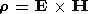 | (13) |
where
H is the geomagnetic field strength.
In the earlier works by
Zhovty et al. [1997] and
Chernigovskaya and Zhovty [1998]
similar calculations of
the energetics characteristics were carried out for the summer
solstice period (June 22) of each year from 1976 to 1986, which
corresponds to the 21-st solar cycle. In this paper we made a more
comprehensive analysis of the energy parameter variations for all
seasons of the 22-nd solar cycle.
 The kinetic energy of neutral particles varies within a cycle
of
solar activity directly proportional to the solar activity level.
For example, during the summer solstice at minimum solar activity
(1986) the maximum value of the kinetic energy of neutrals at 90 km
was
W = 0.1 J m
-3 (Figure 1a), whereas during the solar activity
maximum (1989) it was
W = 0.16 J m
-3 at the same height (Figure 1c).
The height increasing the kinetic energy of neutral particles
decreases very rapidly. At
h = 130 km we have
W
The kinetic energy of neutral particles varies within a cycle
of
solar activity directly proportional to the solar activity level.
For example, during the summer solstice at minimum solar activity
(1986) the maximum value of the kinetic energy of neutrals at 90 km
was
W = 0.1 J m
-3 (Figure 1a), whereas during the solar activity
maximum (1989) it was
W = 0.16 J m
-3 at the same height (Figure 1c).
The height increasing the kinetic energy of neutral particles
decreases very rapidly. At
h = 130 km we have
W 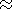 0.8
0.8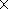 10-4 J m
-3,
that is, the energy of neutrals has decreased by three
orders of magnitude as compared to the height of 90 km (Figure 1b, d).
This is due to the rapid decrease in the atmospheric density
with height. The peaks of
W lying in the equatorial region and
decreasing towards middle latitudes, which are observed in the
spatial distribution of the kinetic energy of neutrals, are related
to the latitudinal variations in the neutral density in the Earth's
atmosphere, as well as in the neutral wind velocity at the heights
under consideration. Temporal variations of
W show clear maxima
during the nighttime, morning and evening hours, which are caused
by the diurnal variation in the neutral atmosphere density.
10-4 J m
-3,
that is, the energy of neutrals has decreased by three
orders of magnitude as compared to the height of 90 km (Figure 1b, d).
This is due to the rapid decrease in the atmospheric density
with height. The peaks of
W lying in the equatorial region and
decreasing towards middle latitudes, which are observed in the
spatial distribution of the kinetic energy of neutrals, are related
to the latitudinal variations in the neutral density in the Earth's
atmosphere, as well as in the neutral wind velocity at the heights
under consideration. Temporal variations of
W show clear maxima
during the nighttime, morning and evening hours, which are caused
by the diurnal variation in the neutral atmosphere density.
The rate of energy release
Q, caused by the dissipation of
ionospheric currents, undergoes significant spatial and temporal
variations
[Chernigovskaya and Zhovty, 1998].
Joule
(frictional) heating is maximum at altitudes of 130-140 km. A
pronounced maximum around the noon is seen in the diurnal
variation. These features in the variations of
Q are independent of
the season and manifest themselves during all phases of the solar
activity cycle.
 In addition to the general features, significant seasonal
and
latitudinal variations of the Joule heating rate are observed.
Figure 2
shows spatial and temporal distributions of
Q for the
period of the solar activity maximum in 1989, in winter (Figure 2a, b, c)
and summer (Figure 2d, e, f)
solstice conditions. Differences
between the summer and winter hemispheres are visually seen. The
largest peaks of
Q occur at the high-latitude boundary of the
summer hemisphere. The midlatitude region shows a gradual decrease
of the energy release rate in the direction from the high-latitude
boundary. A small maximum of
Q is observed in the near-equatorial
regions and seems to be associated with the presence there of the
equatorial electrojet.
In addition to the general features, significant seasonal
and
latitudinal variations of the Joule heating rate are observed.
Figure 2
shows spatial and temporal distributions of
Q for the
period of the solar activity maximum in 1989, in winter (Figure 2a, b, c)
and summer (Figure 2d, e, f)
solstice conditions. Differences
between the summer and winter hemispheres are visually seen. The
largest peaks of
Q occur at the high-latitude boundary of the
summer hemisphere. The midlatitude region shows a gradual decrease
of the energy release rate in the direction from the high-latitude
boundary. A small maximum of
Q is observed in the near-equatorial
regions and seems to be associated with the presence there of the
equatorial electrojet.
 A separated study of variations of the Joule heating rate
for
different latitudes of the northern hemisphere and different
seasons over within solar activity cycles was performed. Figure 3
presents the vertical
Q profiles for the summer season for the
periods of minimum (1986, 1996) and maximum (1989, 1991) solar
activity at the high-latitude boundary of the region under
consideration ( q = 25o ), for the midlatitude
region
( q = 45o), as well as for the
near-equatorial region
(q =75o).
An increase of the energy release rate with increasing
level of solar activity is visually seen for all latitudes. This is
especially typical of the high-latitude regions where the Joule
energy release rate can increase by as much as an order of
magnitude while passing from the phase of minimum solar activity to
the phase of maximum activity (Figure 3a). For instance,
Q
A separated study of variations of the Joule heating rate
for
different latitudes of the northern hemisphere and different
seasons over within solar activity cycles was performed. Figure 3
presents the vertical
Q profiles for the summer season for the
periods of minimum (1986, 1996) and maximum (1989, 1991) solar
activity at the high-latitude boundary of the region under
consideration ( q = 25o ), for the midlatitude
region
( q = 45o), as well as for the
near-equatorial region
(q =75o).
An increase of the energy release rate with increasing
level of solar activity is visually seen for all latitudes. This is
especially typical of the high-latitude regions where the Joule
energy release rate can increase by as much as an order of
magnitude while passing from the phase of minimum solar activity to
the phase of maximum activity (Figure 3a). For instance,
Q 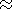 (6
(6 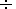 12)
12)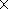 10-10 W m
-3 during the solar activity minimum in 1986
and 1996, and
Q
10-10 W m
-3 during the solar activity minimum in 1986
and 1996, and
Q 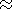 (120
(120 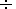 140)
140)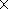 10-10 W m-3 in the maximum
activity years (1989 and 1991). The figures show a distinct
decrease of the Joule energy release rate while moving from the
high-latitude boundary to the equator (Figure 3a, b, c).
10-10 W m-3 in the maximum
activity years (1989 and 1991). The figures show a distinct
decrease of the Joule energy release rate while moving from the
high-latitude boundary to the equator (Figure 3a, b, c).
 The instantaneous electromagnetic energy flux density
P0 reaches a maximum value ~0.5 W m
-3 during the summer solstice
in the solar activity maximum. No pronounced qualitative
differences in space-time distributions of the Poynting's vector
components in different seasons was observed. As an example,
Figure 4
presents a pictures of latitude-time distributions of the zonal
and meridional components of
P0 for the minimum (1986) and
maximum (1989) of solar activity for the winter solstice
conditions. The energy transport is more intense in the zonal
direction (Figure 4a, c).
At solar activity minimum during the most
part of the 24-hour period in the near-equatorial and midlatitude
ionosphere is directed eastward ( P0l > 0), except during
the morning hours (Figure 4a). With an increase of solar activity
there appears in this latitude range a region of intense westward
transport of the electromagnetic energy
(P0l < 0) in the
daytime and in the evening hours (Figure 4c). At higher latitudes
electromagnetic energy is transported westward nearly throughout 24
hours. The energy input from the magnetosphere through the
high-latitude regions occurs at night and in the daytime (positive
values of the meridional component
P0q correspond to a
southward flux at the high-latitude boundary) (Figure 4b, d). In
the dawn and dusk (after about 1800 LT) hours the electromagnetic
energy flows from the midlatitude ionosphere towards the poles.
There is a tendency of the meridional energy flux density
P0q to decrease from the high-latitude
boundaries of the
region considered to the equator.
The instantaneous electromagnetic energy flux density
P0 reaches a maximum value ~0.5 W m
-3 during the summer solstice
in the solar activity maximum. No pronounced qualitative
differences in space-time distributions of the Poynting's vector
components in different seasons was observed. As an example,
Figure 4
presents a pictures of latitude-time distributions of the zonal
and meridional components of
P0 for the minimum (1986) and
maximum (1989) of solar activity for the winter solstice
conditions. The energy transport is more intense in the zonal
direction (Figure 4a, c).
At solar activity minimum during the most
part of the 24-hour period in the near-equatorial and midlatitude
ionosphere is directed eastward ( P0l > 0), except during
the morning hours (Figure 4a). With an increase of solar activity
there appears in this latitude range a region of intense westward
transport of the electromagnetic energy
(P0l < 0) in the
daytime and in the evening hours (Figure 4c). At higher latitudes
electromagnetic energy is transported westward nearly throughout 24
hours. The energy input from the magnetosphere through the
high-latitude regions occurs at night and in the daytime (positive
values of the meridional component
P0q correspond to a
southward flux at the high-latitude boundary) (Figure 4b, d). In
the dawn and dusk (after about 1800 LT) hours the electromagnetic
energy flows from the midlatitude ionosphere towards the poles.
There is a tendency of the meridional energy flux density
P0q to decrease from the high-latitude
boundaries of the
region considered to the equator.
4. Discussion and Conclusions
The simulations with the help of the self-consistent (in terms of
the parameters considered) numerical model for the ionospheric
dynamics and electrodynamics have revealed some features of the
spatial and temporal variations in energetic characteristics within
a solar cycle under quiet geomagnetic conditions. Some of these
features were described in the earlier work
[Chernigovskaya and Zhovty, 1998;
Zhovty et al., 1997]
while analyzing
the energy parameter variations under summer solstice conditions
during the 21-st solar activity cycle. However, the results
presented here made it possible to refine earlier assumptions,
because this version of the numerical model uses a more accurate
and comprehensive neutral atmosphere model
[Hedin, 1987].
The kinetic energy of neutral species varies within a solar
activity cycle directly proportional to the changes of the activity
level.
The Joule heating is maximum at 130-140 km. The diurnal variation
shows a distinct maximum around the noon. These features in
Q variations are independent of the season and manifest themselves
during all phases of a solar activity cycle.
However, there are significant seasonal, latitudinal and
heliocyclic variations of
Q. The rate of the energy release due to
the ionospheric current dissipation tends to increase with an
increase of solar activity. Differences between the summer and
winter hemispheres in the energy release due to the Joule heating
are well pronounced. A peak in
Q occurs at the high-latitude
boundary of the summer hemisphere during the solar activity
maximum. In the midlatitude region the energy release rate
decreases gradually equatorward.
The features of the Joule heating rate variations mentioned above
are caused by the change in the potential electric field strength
which depends on the electromotive force (EMF) induced by the
neutral particle mass fluxes in the northern and southern
hemispheres, as well as by the spatial-temporal characteristics and
seasonal variations of the Pedersen conductivity distribution.
According to the numerical calculations presented the
hemisphere-averaged integral energy
Q released due to the Joule
heating per unit time is
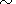 2.72
2.72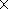 1010 W.
This value agrees
well with the hemisphere-averaged Joule heating
Q
1010 W.
This value agrees
well with the hemisphere-averaged Joule heating
Q 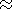 2.5
2.5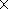 1010 W for
Kp = 1 at equinox given by
Foster et al. [1983],
and is close to the estimates by
Bryunelli and Namgaladze [1988].
1010 W for
Kp = 1 at equinox given by
Foster et al. [1983],
and is close to the estimates by
Bryunelli and Namgaladze [1988].
Foster et al. [1983]
investigated also seasonal variations
in the Joule heating and found a small differences between the
hemispheres for similar seasons, but a significant predominance (by
about 50%) of the Joule heating generated in the summer hemisphere
over that in the winter hemisphere due to enhanced summer
ionospheric conductivities produced by solar ionization. These
results agree well with the conclusions in this study.
The instantaneous density of the electromagnetic energy flux
P0 reaches a maximum value of about 0.5 W m
-3 during the
summer solstice at solar activity maximum. The energy transport is
more intense in the zonal direction. The input of energy from the
magnetosphere to the ionosphere through the high-latitude regions
occurs at night and in the daytime. In the dawn and dusk (after
about 1800 LT) hours the electromagnetic energy flows out of the
midlatitude ionosphere towards the poles. The density of the
meridional energy flux tends to decrease from the high-latitude
boundaries to the equatorward.
The results obtained make it possible to analyze energy
characteristics for heights of the lower thermosphere which are
particularly poorly known, but are of most importance.
Evaluation of the inputs from different kinds of energy to the
thermosphere and ionosphere is of a great importance for
understanding the thermal structure and dynamics of the neutral
atmosphere and the ionosphere. The amount of electromagnetic energy
dissipated in the ionosphere, especially during strong geomagnetic
disturbances, often exceeds the contribution from other sources
energy (the tidal heating, heating by solar UV-radiation, energy of
the particles precipitating from the magnetosphere). This
phenomenon is due to the characteristics of the Pedersen
conductivity height profile which are responsible for a fairly high
Joule heating of the ionosphere at certain altitudes. Under quiet
geomagnetic conditions, however, the energy release caused by the
ionospheric currents dissipation, is also an important source of
the energy input to the ionosphere. On the other hand, a study of
the spatial-temporal distribution of the Poynting's vector flux
provides a visual illustration how the electromagnetic energy is
transported between the various ionospheric regions and levels and
how the coupling with other regions of the Earth's space
environment occurs. The importance of studies of this problem have
been repeatedly noted by many authors
[Fedder, 1991;
Kelley et al., 1991].
The results of numerical simulation can also be useful whice
planning and interpreting in-situ experiments in the Earth's space
environment and investigating variations in ionospheric dynamics
and electrodynamics associated with long-term trends of geophysical
and heliophysical conditions.
References
Bryunelli, B. E., and A. A. Namgaladze,
Physics of the Ionosphere (in Russian),
528 pp., Nauka, Moscow, 1988.
Chernigovskaya, M. A., and E. I. Zhovty, Energetics in the
mesosphere-thermosphere-ionosphere system in quiet conditions,
Geomagn. Aeron. (in Russian), 38 (1), 129, 1998.
Ching, B. K., and Y. T. Chiu, A phenomenological model of global
ionosphere electron density in the
E,
F1, and
F2 regions,
J. Atmos. Terr. Phys., 35 (9), 1615, 1973.
Fedder, J. A., Ionospheric coupling from a global perspective,
EOS, 72 (44), 359, 1991.
Foster, J. C., J.-P. St.-Maurice, and V. J. Abreu, Joule heating at
high latitudes,
J. Geophys. Res., 88, 4885, 1983.
Gurevich, A. V., and E. E. Tsedilina, Dynamics of fast electron and
ion irregularities in the Earth's magnetosphere,
Geomagn. Aeron. (in Russian), 9 (3), 458, 1969.
Hedin, A. E., MSIS 86 thermospheric model,
J. Geophys. Res., 92, 4649, 1987.
Jacchia, L. G., Thermospheric temperature, density, and
composition: New models,
Special Rep. 375, 106 pp., Smithsonian
Institute Astrophysical Observatory, Cambridge, Massachusetts,
1977.
Kelley, M. C., D. J. Knudsen, and J. F. Vickrey, Poynting flux
measurements on a satellite: A diagnostic tool for space research,
J. Geophys. Res., 96, 201, 1991.
Killeen, T. L., Energetics and dynamics of the Earth's
thermosphere,
Rev. Geophys., 25 (3), 433, 1987.
Krinberg, I. A., and A. V. Tashchilin,
The Ionosphere and Plasmasphere (in Russian), 190 pp., Nauka, Moscow,
1984.
Krylov, A. L., and V. P. Shcherbakov, On equations of potential
electric fields in the magnetosphere and ionosphere,
Geomagn. Aeron. (in Russian), 12 (2), 218, 1972.
Richmond, A. D., Thermospheric dynamics and electrodynamics,
in
Solar-Terrestrial Physics, pp. 523-607,
1982.
Richmond, A. D., et al., An empirical model of quiet-day
ionospheric electric fields at middle and low latitudes,
J. Geophys. Res., 85, 4658, 1980.
Samarsky, A. A.,
Introduction to the Theory of Difference Schemes (in Russian),
552 pp., Nauka, Moscow, 1971.
Samarsky, A. A., and E. S. Nikolaev,
Methods of Solving Network Equations (in Russian), 592 pp., Nauka, Moscow,
1978.
Singh, A., and K. Cole, A numerical model of the ionospheric
dynamo, I, Formulation and numerical technique,
J. Atmos. Terr. Phys., 49 (6), 521, 1987.
Zhovty, E. I., and M. A. Chernigovskaya, Formation of a global
ionospheric drifts system with the inclusion of the transport
processes effect on the ionization distribution in the
F region,
Issled. Geomagn. Aeron. Fiz. Solntsa, 92 (in Russian),
25,
Irkutsk
University, Irkutsk,
1990.
Zhovty, E. I., M. A. Chernigovskaya, and N. K. Barsukova, On a
calculation of the wind system of thermospheric sources in a
quasi-stationary approximation,
Issled. Geomagn. Aeron. Fiz. Solntsa, 67 (in Russian),
77,
Irkutsk University, Irkutsk,
1984.
Zhovty, E. I., M. A. Chernigovskaya, and E. S. Kazimirovsky,
Energetics in the mesosphere-thermosphere-ionosphere system under
quiet conditions,
Adv. Space Res., 20 (6), 1197, 1997.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.2.0) on November 27, 2000.
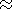 ni )
ionospheric plasma, and of the electric field and
current formed as a result of a given pressure gradient of the
neutral gas and an electric field applied from outside, the
distributions of atmospheric and ionospheric parameters at the
heights of
E and
F regions of the middle- and low-latitude
ionosphere under undisturbed geomagnetic conditions being known.
The geomagnetic field is
assumed to be a geocentric dipole field.
ni )
ionospheric plasma, and of the electric field and
current formed as a result of a given pressure gradient of the
neutral gas and an electric field applied from outside, the
distributions of atmospheric and ionospheric parameters at the
heights of
E and
F regions of the middle- and low-latitude
ionosphere under undisturbed geomagnetic conditions being known.
The geomagnetic field is
assumed to be a geocentric dipole field.
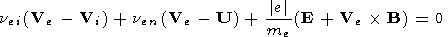
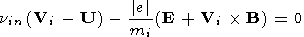
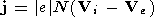

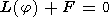
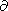 /
/ 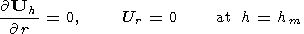

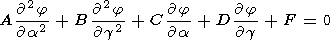
 s1,
s2 (s0,
s1, and
s2 are the field-aligned, Pedersen,
and Hall conductivities,
respectively) and that there is no current across the lower
boundary (see equation (8)). The boundary condition for the
potential on the equatorial boundary
a = amin
= 1, as
well as on the high-latitude boundary
a = amax
= 5.7,
was defined from the observational data
[Richmond et al.,
s1,
s2 (s0,
s1, and
s2 are the field-aligned, Pedersen,
and Hall conductivities,
respectively) and that there is no current across the lower
boundary (see equation (8)). The boundary condition for the
potential on the equatorial boundary
a = amin
= 1, as
well as on the high-latitude boundary
a = amax
= 5.7,
was defined from the observational data
[Richmond et al., 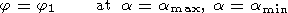
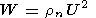
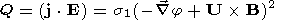
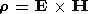

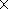 10-4 J m
-3,
that is, the energy of neutrals has decreased by three
orders of magnitude as compared to the height of 90 km (
10-4 J m
-3,
that is, the energy of neutrals has decreased by three
orders of magnitude as compared to the height of 90 km (

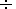 12)
12)
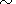 2.72
2.72