
RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 20, ES1007, doi:10.2205/2020ES000690, 2020
Xuan-Nam Bui1, Trong Dinh Cao2, Long Quoc Nguyen1, Bach Xuan Mai2, Le Hung Trinh3, Hien Phu La4, Ropesh Goyal5, Tuan Anh Thai2, Hung Nam Pham2
1Hanoi University of Mining and Geology, Hanoi, Vietnam
2Institute of Geophysics, VAST, Hanoi, Vietnam
3Le Quy Don Technical University, Hanoi, Vietnam
4Thuy Loi University, Hanoi, Vietnam
5Department of Civil Engineering, Indian Institute of Technology, Kanpur, India
The paper presents the assessment of the maximum magnitude of natural and triggered earthquakes when water is impounded to 130 m in the mining pit for the landscaped lake in the Nui Nho quarry in Di An commune, Binh Duong province, Vietnam. The maximum magnitudes of the natural and triggered earthquakes were estimated by using artificial neural network and source segmentation methods, respectively. Gravity method was used to estimate fault parameters including strike, dip and rake angles. As well as, these fault parameters are considered as input information to compute the influence of Nui Nho reservoir impoundment by using the concept of fault stability Coulomb stress in order to assess risk of triggered earthquake occurrence. The results show that the Nui Nho quarry is within the sphere of influence of second order Dong Nai River fault zone; the magnitude of natural earthquake that can occur in this area is 5.0; the triggered earthquake source of Nui Nho lake has the length of 4.8 km and the width of 1.8 km; the maximum magnitude of triggered earthquake can only be less than or equal to 3.2; the reservoir with depth of 130 m can cause direct stress on the lake bottom with the maximum value of 47.295 kPa and Coulomb stress field with the value of 4.338 kPa. The region of positive Coulomb stress shows the influence of reservoir impoundment indicating the region of risk of triggered earthquakes occurrence.
Scientists have found that artificial lakes with considerable depths (e.g. over 90 m) can possibly cause earthquakes [Gupta, 2002, 2011; Gupta et al., 1972; Kalpna and Chander, 2000; Kalpna and Gupta, 2008; Kalpna et al., 2016]. The weight of water mass buckles the basement rock of lake bottom, causing subsidence (the subsidence of lake bottom can be up to $1.5\div 2$ m), which is the reason for triggering the reactivation of faults in the region, increasing the horizontal permeability, especially in the fracture zones. The increase of pore pressure in rock increases the infiltration, thus reducing the friction of existing conformities or failure surfaces. As a result, it decreases the firmness and changes the elastic coefficient of rock, causes the fluctuation of preceding tension force, leading to the displacement of rock mass towards the tectonic failure surface [Gupta, 2002, 2011; Gupta et al., 1972; Hagan et al., 1996; Hojjat and Panakkat, 2009; Kalpna and Chander, 2000; Kalpna and Gupta, 2008; Kalpna et al., 2016].
Triggered earthquake does not occur in all the lakes. It only occurs in the lakes with favorable geological and tectonic conditions: they are active zones, the tectonic stress in rock reaches the limit, the faults hydrologically related to the lakes are large enough. In case the stress reaches the limit, the incremental stress caused by reservoir loading can play a role as the promoting mechanism although it is very small. According to statistics [Hagan et al., 1996], the percentage of lakes with a depth of $90 \div 120$ m in which triggered earthquake can occur is 6% (5/78 lakes); that with a depth of $120 \div 150$ m is 17% (5/29 lakes) and that with a depth of $150 \div 250$ m is 26% (5/19 lakes). Triggered earthquakes have also occurred at some hydropower reservoirs in Vietnam, most notably in Hoa Binh, Song Tranh 2 and Son La [Pupkov et al., 2012; Son, 2012;
Trong, 2012; Telesca et al., 2016; Tuan et al., 2017]. On 23 May 1989 an earthquake with $M = 4.9$ occurred in Hoa Binh area after impounding water in the hydropower reservoir to the maximum elevation (90 m). Shortly after the Song Tranh 2 hydropower reservoir was impounded (up to 96 m height), triggered earthquakes occurred, with the largest magnitude $M = 4.7$ on 15 November 2012. The strongest triggered earthquake at Son La hydropower reservoir has a magnitude of 4.3, recorded on 19 July 2014. The geological structures of Hoa Binh, Song Tranh 2 and Son La reservoirs are metamorphic rocks (including gneiss, metagabbro, metadiorite, metagranodiorite, metaplagiogranite), granite, andesite or strongly cataclastic, fractured compact limestone.
The Nui Nho quarry in Di An commune, Binh Duong province is currently exploited at $-100$ m. In the future, this quarry will be exploited to $-130$ m and converted into a landscaped lake. Does the water impoundment in a lake of such great depth cause triggered earthquake? The managers and scientists in Binh Duong province claim that the geological and tectonic characteristics of Nui Nho are similar to those of Song Tranh 2, where the triggered earthquakes have occurred frequently after the water impoundment. Natural earthquakes have not been recorded in Nui Nho quarry; similarly, in Song Tranh 2, there have never been natural earthquakes before the occurrence of triggered earthquakes. That is the question that needs to be answered before the depth of exploitation and conversion of utility are approved. The assessment of the maximum magnitude of natural earthquake plays an important role in calculating earthquake hazard and determining the maximum magnitude of the triggered earthquake if it occurs. The maximum magnitude of the triggered earthquake does not exceed that of natural earthquakes in the study area [Son, 2012; Trieu et al., 2014; Trong et al., 2016; Tuan et al., 2017]. In this paper, a comprehensive study is described which estimates source parameters, maximum magnitude of natural and triggered earthquakes. The authors present in detail the modern approach, using artificial intelligence (artificial neural network) in assessing the maximum magnitude of natural earthquakes in the study area. The gravity method was used to estimate source dimension to calculate the maximum triggered earthquake. Finally, modelling of Coulomb stresses due to reservoir water loading has been used to see the effect of reservoir impoundment in the Nui Nho area.
Xuyen [2004] and Trieu [2010a, 2010b] argued that the earthquake activities in the Nui Nho quarry and adjacent area in particular and in Southern Vietnam in general are not strong compared to in extreme Northwestern Vietnam and the earthquake magnitude here does not exceed 6.0. According to historical records, some earthquakes with $M = 5.0$ also occurred in this area before the 20th century, for example in 1715 ($M = 4.0 \div 5.0$), in 1877 ($M = 5.0 \div 5.5$), 1882 ($M = 5.0 \div 5.5$). The Institute of Geophysics (Vietnam Academy of Science and Technology) manages the earthquake data in Vietnam and has responsibility for updating annual earthquake data
[Trieu, 2010a, 2010b; Xuyen [2004]. Due to the war and the lack of attention to earthquakes in historical records, the earthquake catalogue obtained in the Institute of Geophysics is deficient in data and the accuracy of $M$ determination is also low. The error of $M$ determination according to historical records and public surveys is probably not less than 1.0 $M$ unit. Only after 2002 when 7 earthquake observation stations were established in this area, there has been sufficient information about earthquakes with $M \geq 3.5$ [Hung, 2009; Trieu, 2010a, 2010b]. Therefore, in order to have the best earthquake catalogue for maximum natural earthquake forecasting (Mmax) in the Nui Nho quarry and adjacent area, the authors have collected more earthquake data of ISC
 |
| Figure 1 |
(http://www.isc.ac.uk/iscbulletin/search/bulletin/ interactive/). CN algorithm [Peresan et al., 2000; Trieu, 2010b] is used to analyze, compare and produce the most reliable earthquake catalogue from 1900 to 2017 (Figure 1).
The feedforward neural network with backpropagation algorithm was applied to calculate the maximum magnitude of natural earthquake [Bhatia, 2018; Hagan et al., 1996; Hojjat and Panakkat, 2009; Pupkov et al., 2012; Trong et al., 2016]. Input data for calculation include: 1) Gradient value of elevation; 2) Gradient value of Bouguer gravity field (Vietnam Geophysical Divison, 2010); 3) Gradient of aeromagnetic anomaly (Vietnam Geophysical Divison, 1995); 4) Gradient value of isostatics [Trieu, 2010b]; 5) Gradient of sedimentary crust thickness [Hung, 2009]; 6) Gradient of crystalline basement depth [Hung, 2009]; and 7) Gradient of the Earth's crust thickness [Hung, 2009]. The distribution map of maximum magnitude of natural earthquake (Mn.max) according to our calculation result is shown in Figure 1.
Input parameters are the data that are assessed as directly related to the earthquake magnitude. Standard samples are typical earthquakes with magnitude greater than or equal to 2.5 and with earthquake catalogue from 1900 to 2017. The analysis and processing of input data for calculating and forecasting maximum natural earthquake (Mtn.max) are conducted as follows: Firstly, the study area is divided into the square grid with side of 0.5 km; then, the data matrix is established based on the result of analysis of 7 existing data at the grid points. The investigation and selection of neural network are carried out in accordance with the strict process [Trong, 2012, 2019; Trong et al., 2019].
According to the neural network construction algorithm, among 100% of the samples, we take 70% to build network parameters, 15% to check the rationality and the remaining 15% to recheck the network. For each of the above percentages there is an evaluation $R$; after synthesizing and averaging we get the result $R$ of neural network. It should be noted that due to the limited number of earthquakes observed, we have to increase the study area to ensure the representativeness of earthquake magnitude. The forecasting result (Mtn.max) presented in Figure 1 shows that:
 |
| Figure 2 |
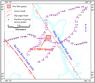
Previous studies have suggested that the Nui Nho quarry is located in Dong Nai River active fault zone. Sai Gon River active fault zone is in the southwest of Nui Nho quarry (Figure 2). Both faults can possibly cause earthquakes [Hung, 2009; Linh et al., 2008; Trieu, 2010a, 2010b; Xuyen, 2004], however, the segment of Dong Nai River active fault zone in Nui Nho quarry is the source of triggered earthquake when water is impounded to 130 m high.
The authors have used empirical formulas on the relationship between source parameters (volume, width, length) and maximum earthquake magnitude by Wells and Coppersmith [1994] and Trieu [2010b]. Therefore, it is necessary to determine the structural characteristics of sources which can possibly cause triggered earthquake.
High-precision gravity method was chosen to determine earthquake source parameters in Nui Nho quarry, based on the opinions that rocks are strongly fractured when water penetrates the ground and changes pore pressure, which is the cause of earthquake [Gupta, 2002, 2011; Gupta et al., 1972; Kalpna and Chander, 2000; Kalpna and Gupta, 2008; Kalpna et al., 2016]. Meanwhile, the strongly fractured zone is easily recognized through low value of normalized full gradient $GH (x, z)$ compared to monolithic environment [Trong et al., 2016]. The boundary of this zone is also determined by the maximum horizontal gradient of Bouguer gravity anomaly (Gmax) at different depths [Trong et al., 2016].
 |
| Figure 3 |
Based on the measurements of 3 highly detailed gravity profiles (Figure 2, 1000 measurement points, the scale of 1/50,000), 2 best profiles of cross-sectional analysis are selected to determine the parameters of sources which can cause triggered earthquakes (Figure 3a–Figure 3b). The study results allow determining the structural characteristics of earthquake source [Trong et al., 2019]: width of 2.8 km, depth of 12 km, and dip of $80\mbox{°}$ for natural earthquake source; width of 1.8 km, depth of 12 km, and dip of 80° for triggered earthquake source (in which rocks are fractured more strongly and penetrated more easily by water when connected to reservoir). These parameters are used in determining maximum triggered earthquake (Mt.max).
Vietnamese seismologists often use the empirical formulas of Wells and Coppersmith [1994] and Trieu [2010b] in assessing the values of maximum earthquakes for the regions with inadequate earthquake data. Although these two formulas have different coefficients, they have the same result [Hung, 2009; Trieu, 2010a, 2010b; Trong et al., 2019]. These two formulas are also used for the Nui Nho quarry. Calculation results show that:
There are 3 major effects of reservoir loading associated with triggered earthquake: 1) The changes of elastic stress related to water impoundment of reservoir; 2) The increase of pore pressure in water-saturated rocks (due to the reduction of pore volume caused by compression) in the reaction to the increase of elastic stress; and 3) The changes of pore pressure related to water permeability.
To calculate the incremental stress and subsidence of the reservoir bottom, both 2D and 3D problems can be used [Kalpna and Chander, 2000; Kalpna and Gupta, 2008; Kalpna et al., 2016]. In the case of the 3D problem, the reservoir is subdivided into the area elements of $(a) \times (a)$ km$^2$ by a set of orthogonal straight lines. After determining the water depth ($hi$) for each area element, we have the vertical force $Fi = \rho g a^2hi$ at the center of each area that can replace the water column pressure. With the $X'X$ axis towards the east, the $Y'Y$ axis towards the north and the $Z'Z$ axis downwards, 3 normal stress components and 1 tangential stress component at any point $P$ are calculated according to the following formulas:
\begin{eqnarray*} \sigma_r = \frac{F}{2\pi} \Bigl[ \frac{1 - 2\gamma}{r^2} \Bigl( 1 - \frac{z}{R} \Bigr) - \frac{3r^2 z}{R^5} \Bigr] \end{eqnarray*} \begin{eqnarray*} \sigma_z = \frac{3F}{2\pi} \frac{z^3}{R^5} \end{eqnarray*} \begin{eqnarray*} \sigma_{\theta} = \frac{F}{2\pi} (1 - 2\gamma) \Bigl( -\frac{1}{r^2} + \frac{z}{r^2 R} + \frac{z}{R^3} \Bigr) \end{eqnarray*} \begin{eqnarray*} \tau_{xz} = -\frac{3F}{2\pi} \frac{rz^2}{R^5} \end{eqnarray*}where: $\nu$ is Poisson's ratio; $R = \sqrt{x^2 + y^2 +z^2}$ – the distance from the origin to the point $P(x,y,z)$ and its projection given by $r = \sqrt{x^2 + y^2}$.
To add the distribution of $F$ forces, converting to Cartesian coordinate system according to the correlation:
\begin{eqnarray*} \begin{array}{ll} \sigma_x = &\tau_{xy} = \sigma_{\theta} \sin^2 \theta + \sigma_r \cos^2 \theta & (\sigma_r - \sigma_{\theta}) \sin \theta \cos \theta \sigma_y = & \tau_{xy} = \sigma_r \sin^2 \theta + \sigma_{\theta} \cos^2 \theta & (\sigma_r - \sigma_{\theta}) \sin \theta \cos \theta \sigma_z = \sigma_z & \tau_{yz} = \tau_{rz} \sin \theta \end{array} \end{eqnarray*}where: the azimuth $\theta = \arctan (y/x)$ is calculated from the east to the north (counterclockwise). Stress is considered as the result of total loading on a point collected by taking the total distribution of all $F$ forces for 6 stress components: $\sigma_x$, $\sigma_y$, $\sigma_z$, $\tau_{xy}$, $\tau_{yz}$, $\tau_{zx}$. From these parameters, we select the downward normal stress $\sigma_z$ and the maximum tangential stress $\tau_{\max} = (\sigma_1 - \sigma_3$). In addition, under the pressure of reservoir loading, the vertical subsidence $\Delta d (m)$ due to the effect of total force $F$ is calculated by the formula:
\begin{eqnarray*} \Delta d = \frac{F}{2\pi E} \Bigl[ \frac{(1+\upsilon) Z^2}{R^3} + 2 \frac{(1-\upsilon^2)}{R} \Bigr] \end{eqnarray*}
where: $E$ is Young's modulus; $R$ is the distance of point $P$ from the origin. The subsidence is caused by all the point forces and the total subsidence $d$ at point $P$ is the result of reservoir loading.
 |
| Figure 4 |
 |
| Table 1 |
The calculation of incremental stress on the bottom of the Nui Nho reservoir after water impoundment is carried out at the depths of 2 km, 4 km, 6 km, and 8 km (thehypocenter of the triggered earthquake is usually located at the depth of 2 km to 8 km). The results of stress calculation at different depths with water columns of 100 m and 130 m are presented in (Figure 4a–Figure 4d), and the maximum value of this incremental stress is shown in Table 1.
According to Bell and Nur [1978], the change of Coulomb stress($\Delta S$) caused by water impoundment in the reservoir is determined as follows: $\Delta S = \Delta \tau - \mu (\Delta \sigma_n - \Delta P)$, where $\Delta \tau$ and $\Delta \sigma_n$ correspond to the changes of tangential stress and normal stress which are caused by the reservoir loading on the fault surface, $\Delta P$ is the change of pore pressure, and $\mu$ is the coefficient of friction. The increase of $\Delta \tau$ and the decrease of $\Delta \sigma_n$ mean that $\Delta S$ has a positive value, which will stimulate the fault activity and vice versa. The role of pore pressure always promotes the fault activity due to the lubrication on the fault surface and decreases the tangential stress component $\Delta \tau$. Based on the above theoretical basis, the incremental stress and Coulomb stress caused by the reservoir loading have also been modelled to see the effect of reservoir impoundment in the Nui Nho area. The reservoir is subdivided into small blocks, the parameters of length, width and depth at each block are determined. The fault parameters consisting of the strike, dip, and rake are included to calculate the change of stress field. In the study area, Dong Nai River fault near the lake is considered active and the parameters of this fault (strike = 140°, dip = 80°, rake = 180°) are included in the calculation. The study area is gridded into $0.0018\mbox{°} \times 0.0018\mbox{°}$; Poisson's ratio $\nu = 0.25$; Skempton's coefficient $B = 0.7$; coefficient of friction $\mu = 0.65$.
 |
| Figure 5 |
 |
| Table 2 |
Components of Coulomb stress field are calculated with reservoir depths of 100 m and 130 m at the depths of 2 km, 4 km, 6 km, and 8 km, respectively (Table 2, Figure 5a–Figure 5d). The calculation results show that the areas with positive value of Coulomb stress $\Delta S$ are at risk of triggered earthquake when water is fully impounded in the reservoir. On this basis, it is possible to delineate the areas at risk of reservoir-triggered earthquake.
Direct stress and Coulomb stress caused by the highest water column of 130 m have the values of 47.295 kPa and 4.338 kPa, respectively. Compared to the breaking stress of rock in the earthquake (from several hundred bars to several thousand bars), the calculation value is very small, only about 1%. It plays a role as the promoting mechanism and only makes sense when natural stress reaches its limit.
Based on the research results, some following conclusions can be drawn:
Bell, M. L., A. Nur (1978) , Strength changes due to reservoir induced pore pressure and stresses and application to Lake Oroville, J. Geophys. Res., 83, p. 4469–4483, https://doi.org/10.1029/JB083iB09p04469.
Bhatia, A., S. Pasari, A. Mehta (2018) , Earthquake forecasting using artificial neural network, Remote Sensing and Spatial Information Sciences, XLII-5, p. 823–827, https://doi.org/10.5194/isprs-archives-XLII-5-823-2018.
Gupta, H. K., B. K. Rastogi, H. Narain (1972) , Common features of the reservoir associated seismic activities, Bull. Seismol. Soc. Am., 62, p. 481–492.
Gupta, H. K. (2002) , Reservoir induced earthquakes, 64 pp., Elsevier, Netherlands.
Gupta, H. K. (Ed.) (2011) , Encyclopedia of Solid Earth Geophysics, 1539 pp., Springer, Netherlands, https://doi.org/10.1007/978-90-481-8702-7.
Hagan, M. T., H. B. Demuth, M. Beale (1996) , Neural Network Design, PWS Publishing Company, Boston, MA.
Hojjat, A., A. Panakkat (2009) , A probalistic neural network for earthquake magnitude prediction, Neural Networks, 22, p. 1018–1024, https://doi.org/10.1016/j.neunet.2009.05.003.
Hung, C. N. (Ed.) (2009) , Earthquake Microzoning in Ho Chi Minh City. Final Project Report (Stored in South-Vietnam Geological Mapping Division, Institute of Geophysics), 360 pp., Institute of Geophysics, Ho Chi Minh City (in Vietnamese).
Kalpna, G., H. K. Gupta (2008) , An integral equation algorithm for 3-D simulation of pore pressure in a porous elastic medium with heterogeneities, Geophysical Journal International, 175, no. 3, p. 1245–1253, https://doi.org/10.1111/j.1365-246X.2008.03940.x.
Kalpna, G., T. A. Tuan, N. P. Rao (2016) , Rapid and Delayed Earthquake Triggering by the Song Tranh 2 Reservoir, Vietnam, Bull. Seismol. Soc. Am., 106, no. 5, p. 2389, https://doi.org/10.1785/0120160106.
Kalpna, G., R. Chander (2000) , Green's function based stress diffusion solution in the porous elastic half space for time varying finite reservoir loads, Physics of the Earth and Planetary Interiors, 120, p. 93–101, https://doi.org/10.1016/S0031-9201(00)00146-1.
Linh, D. V., V. D. Chinh, L. T. Chich (2008) , The Pliocene – Quaternary tectonic stress field in South Vietnam and its influence on deformation of Precenozoic basement of Cuu Long basin, The 2-nd International Scientific Conference "Fracture Basement Reservoir", 9–10 September 2008, p. 51–62, Petrovietnam, Vung Tau, Vietnam.
Peresan, A., G. F. Panza, G. Costa (2000) , CN algorithm and long lasting changes in reported magnitudes: the case of Italy, Geophys. J. Int., 141, p. 425–437, https://doi.org/10.1046/j.1365-246x.2000.00108.x.
Pupkov, K. A., C. D. Trong, C. D. Trieu (2012) , Attempts at using Neural Network for the prediction of large earthquake in Tay Bac Viet Nam, Bulletin of Bauman Moscow State Technical university, 87, no. 2, p. 70–78.
Son, L. T. (2012) , Study on triggered earthquake forecasting in Son La hydropower reservoir, Final report of state-level independent project, code DTDL.2009T /09, stored in Institute of Geophysics, Institute of Geophysics, Hanoi (in Vietnamese).
Telesca, L., M. Lovallo, C. Lopez, J. M. Molist (2016) , Multiparametric statistical investigation of seismicity occurred at El Hierro (Canary Islands) from 2011 to 2014, Tectonophysics, 672–673, p. 121–128, https://doi.org/10.1016/j.tecto.2016.01.045.
Trieu, C. D. (2010a) , Seismic Activity in Vietnam, 304 pp., Publishing House for Science and Technology, Hanoi (in Vietnamese).
Trieu, C. D. (2010b) , Seismic Hazards in Vietnam, 182 pp., Publishing House for Science and Technology, Hanoi.
Trieu, C. D., L. V. Dung, T. A. Tuan, et al. (2014) , Triggered earthquake study in Tranh River no. 2 (Vietnam), Hydropower Reservoir, Journal Geological Society of India, 84, p. 319–325, https://doi.org/10.1007/s12594-014-0135-x.
Trong, C. D. (2012) , The Application of Neural Network for Earthquake Prediction in Northwest Vietnam, Ph. D. Thesis in Technical Sciences, Bauman Moscow State Technical University, Moscow.
Trong, C. D. (2019) , Triggered earthquake risk assessment when water is impounded in the mining pit of 130 m depth in the Nui Nho quarry and proposal of mitigation solutions, Symposium report (Stored in Institute for Applied Geophysics), Institute for Applied Geophysics, Hanoi (in Vietnamese).
Trong, C. D., N. A. Duong, et al. (2016) , Characteristics of triggered earthquake activity in Da River cascade hydropower plant, Journal of Geology, Series A, 361–362, no. 11–12, p. 80–93 (in Vietnamese).
Tuan, T. A., N. P. Rao, G. Kalpna, et al. (2017) , Evidence that earthquakes have been triggered by reservoir in the Song Tranh 2 region, Vietnam, Journal of Seismology, 21, no. 5, p. 1131–1143, https://doi.org/10.1007/s10950-017-9656-2.
Wells, D. L., K. J. Coppersmith (1994) , New Empirical Relationships Among Magnitude, Rupture Length, Rupture Width, and Surface Displacement, Bulletin of the Seismological Society of America, 84, no. 4, p. 974–1002.
Xuyen, N. D. (2004) , Tectonic geology and strong earthquake-generating areas in the Vietnam's territory, 330 pp., Institute of Geophysics, Hanoi (in Vietnamese).
Received 9 August 2019; accepted 8 November 2019; published 23 February 2020.


Citation: Bui Xuan-Nam, Trong Dinh Cao, Long Quoc Nguyen, Bach Xuan Mai, Le Hung Trinh, Hien Phu La, Ropesh Goyal, Tuan Anh Thai, Hung Nam Pham (2020), Assessment on maximum magnitude of natural and triggered earthquake when water is impounded in the mining pit: A case study in Nui Nho quarry, Vietnam based on gravity and magnetic data, Russ. J. Earth Sci., 20, ES1007, doi:10.2205/2020ES000690.
Copyright 2020 by the Geophysical Center RAS.