RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 18, ES2004, doi:10.2205/2018ES000619, 2018
V. V. Bulatov, Yu. V. Vladimirov
Ishlinsky Institute for Problems in Mechanics RAS, Moscow, Russia
The problem of mathematical modeling of internal gravity wave fields generated by an unsteady perturbation source moving in the stratified ocean of finite depth is considered. Integral forms of the solution are obtained in the linear approximation for a separate wave mode, and it is shown that, at certain generation parameters, the wave pattern of excited internal wave fields represents systems of hybrid wave perturbations which simultaneously have the properties of two waves of the following two types: annular-like (transverse) and wedge-like (longitudinal). The results of numerical simulations describing the basic specific features of the phase structures and wave patterns of the excited fields depending on the generation parameters are presented and discussed.
An important mechanism for exciting fields of internal gravity waves in the ocean is their generation by a source of perturbations of various physical natures, i.e., of the natural (moving typhoon, wind waves, flow over irregularities of the bottom topography, variations in the density and flow fields, leeward mountains) and anthropogenic (offshore technological structures, collapse of the turbulent mixing region, underwater explosions) origin. The system of hydrodynamic equations describing the wave perturbations of stratified media in general form is a quite complicated mathematical problem both in proving the existence and uniqueness theorems in appropriate function classes and from the computational standpoint. The main results of the solution of wave generation problem can be represented in the most general integral form, and in this case the integral solutions require the development of numerical and asymptotic methods for their investigation. These methods allow to carry out a qualitative analysis and express estimations of the solutions. In the framework of the linear theory, the asymptotic methods for integral representations and approximate methods of geometric optics are used to investigate the wave perturbations in natural stratified media analytically [Bulatov and Vladimirov, 2012, 2015a; Massel, 2015; Mei et al., 2017; Morozov, 2018, Pedlosky, 2010; Sutherland, 2010].
To obtain a detailed description of a wide class of physical phenomena related to the dynamics of wave perturbations of inhomogeneous and unsteady ocean, it is necessary to use sufficiently developed mathematical models. The fact that the structures of natural stratified media are three-dimensional also plays an important role, and it is currently impossible to carry out large-scale numerical experiments of three-dimensional ocean flow simulation at large times with a sufficient accuracy. But in several cases, a preliminary qualitative concept of the class of wave phenomena under study can be obtained by using simpler analytical models. In this regard, it is worth noting the classical hydrodynamic problems of constructing asymptotic solutions, which describe the evolution of wave perturbations generated by sources of different nature in heavy liquids. The solutions of such models then allow to represent wave fields with regard to the variability and unsteadiness of real hydro-physical fields in the ocean. Several results of analysis of model linear problems describing various regimes of excitation and propagation of wave perturbations also underlie the nonlinear theory of generation of waves of extremely large amplitude, i.e., of rogue-waves. This theory is currently actively developed [Mei et al., 2017; Morozov, 2018].
The simulation of the dynamics of internal gravity waves is important because of the growing number of offshore platforms in the oil and gas fields. Several cases of offshore platform damage by internal waves of large amplitude should be noted, for example, in the Andaman Sea when, in October, 1997, one of the pillars supporting the platform was bent by a shear flow of an internal wave. The measurements show that the loads caused by internal gravity waves applied to an offshore platform bottom in the vertical direction can be 30 times greater than the loads caused by the wind waves. The internal wave forcing results in the intensive transport of sediments and the bed motions, especially in the regions, where the influence of wind (storm) waves is negligibly small. The internal gravity waves also accelerate the sediment diffusion and the sediment transport in the marine environment. Therefore, the process of particle transport by the flows induced by internal waves are actively studied in different science fields related to hydrobiology (plankton migration, benthos), ecology (propagation of admixtures and impurities), and engineering oceanology [Mei et al., 2017; Morozov, 1995, 2018; Navrotsky, 2013; Vlasenko et al., 2005].
Internal waves in the ocean are three-dimensional, hence, the analysis of two- and three-dimensional unsteady wave motions is a very complicated problem. A numerical code which can solve complete hydrodynamic equations with regard to the real ocean floor relief, the Earth's rotation, and turbulent processes was developed at the Massachusetts Institute of Technology (USA) and was widely adopted. This numerical model requires many computer resources, thus it can be justified only for solving several practical problems in oceanology. Nevertheless, even such complete models do not take into account, for example, the stable horizontally inhomogeneous background stratification existing in the real ocean. To take this hydro-physical effect into account, it is necessary to introduce external forces maintaining this stratification inhomogeneity, but it is rather difficult to parameterize them numerically. The other currently available methods for numerical simulation, including the methods based on the use of supercomputers (IGW Research algorithm, Riemann Solver algorithms for solving hyperbolic equations of shallow water, higher-order pseudo-spectral algorithm for solving hydrodynamic equations HOSM) do not always permit efficiently calculating specific physical problems of wave dynamics of the ocean and atmosphere with regard to their real variability, because they are oriented at solving rather general problems, require high computational power, and do not always take into account the physical nature of the problems under study. In this case it significantly decreases their practical applicability, especially in computations of wave fields in the real natural environment. Moreover, the use of powerful numerical algorithms requires verification and comparison with the solutions of model problems [Abdilghanie et al., 2013; Rees et al., 2012; Tiugin et al., 2012; Vlasenko et al., 2005].
Therefore, simplified and analytical models are widely used in the scientific research and analysis of the wave phenomena in the real stratified ocean. In the linear approximation, the existing approaches to the description of the wave pattern of excited fields of internal waves are based on the representation of the wave fields by Fourier integrals. As a rule, only the first wave mode is considered, because this mode makes the basic contribution to the complete wave field [Bulatov and Vladimirov, 2012, 2015a; Morozov, 2018].
The goal of this paper is the mathematical modeling of unsteady regimes of generation of internal gravity wave fields generated by an unsteady perturbation source moving in the stratified ocean of a finite depth.
In this paper, we consider the problem of mathematical modeling of internal gravity waves generated by the motion of a point perturbation source of power $Q$ in the stratified ocean of depth $H$. We assume that the source power harmonically depends on time $Q=q \exp(i\omega t)$. The source moves with velocity $V$ in the horizontal negative direction along the $x$-axis (the $z$-axis is directed upwards), the depth of the source is $z_0$. The steady-state regime of wave oscillations is considered. In the linear formulation, assuming the Boussinesq approximation, we have the following equation, for example, for the vertical displacement of the isopycnic lines $\eta (x,y,z)$ (lines of equal density with the same harmonic time-dependence) [Bulatov and Vladimirov, 2012, 2015a, 2015b]
\begin{eqnarray*} \bigl( i \omega + V \frac{\partial}{\partial x} \bigr)^2 \Delta\eta + N^2 (z) \Delta_2\eta = \end{eqnarray*} \begin{equation} \tag*{(1)} Q \bigl( i \omega + V \frac{\partial}{\partial x} \bigr) \delta(x) \delta(y) \frac{\partial \delta(z-z_0)}{\partial z_0} \end{equation} \begin{eqnarray*} \Delta = \Delta_2 + \frac{\partial^2}{\partial z^2}, \qquad \Delta_2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} \end{eqnarray*}where
\begin{eqnarray*} N^2(z) = - \frac{g}{\rho_0(z)} \frac{d \rho_0 (z)}{d z} \end{eqnarray*}is the Brunt-Väisälä buoyancy frequency which is further assumed to be constant ($\rho_0(z)$ is the unperturbed ocean density) and $\delta (x)$ is the Dirac delta function.
The problem of adequate and physically justified modeling of natural stratified environment, i.e., the ocean, has been studied in numerous works, because, on the one hand, the widely used models of stratified media described in the scientific literature ($N(z)=$const, the linear or another model distribution of the buoyancy frequency) significantly simplify the mathematical solution of the problem, but on the other hand, problems appear of the adequacy and physical justification of the model representations. The model used here is one of the most widely used models of wave motions in the ocean, because, in certain regions of the World Ocean (Arctic basin), this approximation ($N(z)=$const) gives a good description of the real hydrology and it is one of the basic approximations in real oceanographic and hydro-physical numerical simulations [Bulatov and Vladimirov, 2012, 2015a; Massel, 2015; Morozov, 1995; Pisarev, 1996].
Function $\eta (x,y,z)$ is related to the vertical component of velocity $w (x,y,z)$ as follows:
\begin{eqnarray*} w(x,y,z) = \bigl( i \omega + V \frac{\partial}{\partial x} \bigr) \eta (x,y,z) \end{eqnarray*}[Bulatov and Vladimirov, 2015b]. We use the "rigid lid" boundary condition
\begin{equation} \tag*{(2)} \eta=0 \; \mbox{ at } z=0, -H \end{equation}
In the dimensionless coordinates
\begin{eqnarray*} x^* = x\pi/H, \quad y^* = y\pi/H, \quad z^* = z\pi/H \end{eqnarray*} \begin{eqnarray*} \eta^* = \eta H^2 V/q\pi^2, \quad \omega^* =\omega/N, \quad t^* = tN \end{eqnarray*}Eq. (1) and boundary conditions (2) become (index "*" is omitted)
\begin{eqnarray*} \bigl( i \omega + M \frac{\partial}{\partial x} \bigr)^2 \Delta\eta + \Delta_2\eta = \end{eqnarray*} \begin{eqnarray*} \bigl( i \omega + M \frac{\partial}{\partial x} \bigr) \delta(x) \delta (y) \frac{\partial \delta (z-z_0)}{\partial z_0} \end{eqnarray*} \begin{equation} \tag*{(3)} \eta=0 \; \mbox{ at } z=0, -\pi \end{equation}where $c= NH/\pi$ is the maximum group velocity of internal gravity waves in a layer of stratified medium of thickness $H$, $M=V/c$. The simplest case ($M>1$) is considered in [Bulatov and Vladimirov, 2015b]. It is shown that at a far distance from the oscillating source of perturbations, the excited fields form only a system of wedge-like (longitudinal) waves located inside the corresponding wave fronts. In this paper, we consider a more complicated case: $M<1$.
We seek the solution of problem (3) in the form of the Fourier integral
\begin{eqnarray*} \eta(x,y,z) = \end{eqnarray*} \begin{eqnarray*} \frac{1}{4\pi^2} \int\limits_{-\infty}^{\infty} dv \int\limits_{-\infty}^{\infty} \varphi(\mu,v,z) \exp(-i(\mu x + v y)) d\mu \end{eqnarray*}Then, for determining function $\varphi (\mu, v,z)$, we have the boundary-value problem ($k^2 = \mu^2 + v^2$)
\begin{eqnarray*} \frac{\partial^2 \varphi}{\partial z^2} + k^2 \left( \frac{1}{(\omega-\mu M)^2} -1 \right) \varphi = \end{eqnarray*}\begin{equation} \tag*{(4)} \frac{i}{(\omega-\mu M)} \frac{\partial \delta (z-z_0)}{\partial z_0}, \; \varphi=0 \; \mbox{ at } z=0, -\pi \end{equation}
The solution of problem (4) can be represented as a sum of vertical modes
\begin{eqnarray*} \varphi (\mu, v,z) = \sum_{n=1}^{\infty} \varphi_n (\mu, v,z) = \end{eqnarray*}\begin{eqnarray*} \sum_{n=1}^{\infty} B_n (\mu, v) \cos nz_0 \sin nz \end{eqnarray*} \begin{eqnarray*} B_n (\mu, v) = \end{eqnarray*}
\begin{eqnarray*} \frac{2ni}{\pi(\omega- \mu M)} \; \frac{1}{k^2 ((\omega- \mu M)^{-2} -1) - n^2} \end{eqnarray*}
i.e., as a series in eigen functions of the homogeneous boundary-value problem (4). As a result, the solution of problem (3) becomes
\begin{eqnarray*} \eta(x,y,z) = \sum_{n=1}^{\infty} \eta_n (x,y) \cos nz_0 \sin nz \end{eqnarray*} \begin{eqnarray*} \eta_n(x,y) = \end{eqnarray*}\begin{equation} \tag*{(5)} \frac{1}{4\pi^2} \int\limits_{-\infty}^{\infty} dv \int\limits_{-\infty}^{\infty} B_n (\mu,v) \exp(-i(\mu x + v y)) d\mu \end{equation}
In the expression for function $B_n(\mu, v)$, we equate the denominator to zero to obtain the dispersion relation between the horizontal components $\mu$ and $v$ of wave vector $k$, which can be represented as
\begin{eqnarray*} F_n(\mu, v, \omega,M) =0 \end{eqnarray*} \begin{eqnarray*} F_n(\mu, v, \omega,M) \equiv \end{eqnarray*}\begin{eqnarray*} (\mu M - \omega)^2 - k^2(k^2 + n^2)^{-2}, \; n= 1,2, \ldots \end{eqnarray*}
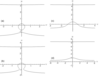
Further, we consider the first mode (index $n =1$ is omitted), $M=0.4$, and the unsteady regimes of internal wave generation corresponding to different values of $\omega$. The frequency range is divided into four intervals as follows: 1) $0<\omega<\omega_1$; 2) $\omega_1 <\omega<\omega_2$; 3) $\omega_2 <\omega<1$; 4) $\omega>1$. Frequency $\omega_1$ is determined by the system of equations
\begin{eqnarray*} F (\mu, 0, \omega,M) =0 \end{eqnarray*}\begin{eqnarray*} \frac{\partial F (\mu, 0, \omega,M)}{\partial \mu} =0, \; \mu <0 \end{eqnarray*}
whose solution gives $\omega_1 = 0.309$. Frequency $\omega_2$ is determined by the system of equations
\begin{eqnarray*} F (\mu, v, \omega,M) =0 \end{eqnarray*}\begin{eqnarray*} \frac{\partial F (\mu, v, \omega,M)}{\partial \mu} =0 \end{eqnarray*}
\begin{eqnarray*} \frac{\partial^2 F (\mu, 0, \omega,M)}{\partial \mu^2} =0 \end{eqnarray*}
 |
| Figure 1 |
whose solution is $\omega_2 = 0.370$. Further, the numerical computations are carried out for the following frequencies of the perturbation source oscillations: $\omega = 0.30$ (the first interval), $\omega = 0.32$ (the second interval), $\omega = 0.66$ (the third interval), and $\omega = 1.12$ (the fourth interval). Figure 1 shows the dispersion relations for these four values of $\omega$. In the first interval, the dispersion curve consists of two unclosed branches and one closed branch. In the second, third, and fourth intervals, there are two unclosed branches. The closed dispersion curves are associated with annular (transverse) waves, and the unclosed dispersion curves are associated with wedge-like waves (longitudinal waves inside the Kelvin wedge).
The residue theorem is used to calculate the inner integral in (5) at the poles of the integrand and the direction of bypassing the poles is determined by the perturbation method. In this case, in the first, third, and fourth intervals, it is convenient to calculate the inner integral in (5) over integration variable $\mu$, and in the second interval, over variable $v$. Then, in each of the four intervals, the determined dispersion curve is associated with its own single integral. For example, in the third interval and in the lower branch of the dispersion curve (Figure 1c), the corresponding single integral (with regard to the harmonic time dependence) becomes
\begin{eqnarray*} J= \frac{1}{2 \pi} \int\limits_{-\infty}^{\infty} A(v) \cos (\mu(v) x + vy - \omega t) dv \end{eqnarray*} \begin{eqnarray*} A(v)= \frac{M}{2} \times \end{eqnarray*}\begin{equation} \tag*{(6)} \frac{( \mu M - \omega)^2}{\mu(v)\omega + Mv^2 + \mu(v)(\mu(v)M-\omega)^3} \end{equation}
where $\mu (v)$ is the lower branch of the dispersion curve in Figure 1c.
The phase structure of the elevation field of generated internal waves for different generation regimes is completely determined by single integrals of form (6) (the other unsteady generation regimes corresponding to different values of $\omega$ are studied similarly). We denote the phase by $ \Phi= \mu (v) x + vy - \omega t$ and use the phase stationary condition $ \mu' (v) = -y/x $ to obtain a family of constant phase line for different values of $\Phi$ with parameter $v$ in the form
\begin{eqnarray*} x= \frac{\Phi + \omega t}{\mu(v) - v \mu' (v)} \end{eqnarray*}\begin{eqnarray*} y = \frac{ \mu' (v) (\Phi + \omega t)}{v \mu' (v) - \mu (v)} \end{eqnarray*}
 |
| Figure 2 |
 |
| Figure 9 |
 |
| Figure 4 |
 |
| Figure 6 |
 |
| Figure 8 |
 |
| Figure 3 |
 |
| Figure 5 |
 |
| Figure 7 |
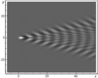
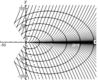
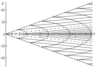
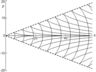
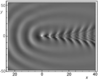
Figure 2–Figure 9 show the results of calculations for the phase structures and wave pattern of the excited internal wave fields at $t=0$. Solid lines in Figure 2, Figure 4, Figure 6, and Figure 8 show the values of phase $\Phi$ multiple of $2 \pi$. The dashed lines in Figure 2, Figure 6, and Figure 8 show the wave front determined by equation $y= \mu' (v^*)/x$, where $v^*$ is a root of equation $\mu^* (v)=0$; in this case, the negative root of this equation is associated with the front line in the upper half-plane, and the positive roots, with the front line in the lower half-plane. The dashed-dotted line in Figure 6 indicates the crest of the wave with zero phase $\Phi$; the equation of this line is $y= \mu' (v^0)/x$, where $v^0$ is a root of equation $ \mu' (v) = y/x$. Figure 2 presents the phase patterns corresponding to the lower and closed branches of the dispersion curve for the first interval. Figure 3 shows the complete wave pattern which is the sum of two corresponding single integrals. It should be noted that the Kelvin wave wedge determined by the upper branches of all dispersion curves (Figure 1) has a very small half-opening angle (of the order of $1^0$) and the wave amplitude determined by these branches is several times smaller than the amplitudes of the waves corresponding to the lower branches of the dispersion curves. Figure 4 and Figure 5 show the phase structure and the wave pattern corresponding to the lower branch of the dispersion curve for the second interval. In this generation regime, the complete field is a hybrid system of waves of the following two types: annular-like (transverse) and wedge-like (longitudinal). Since the amplitude of the perturbation source is unsteady, not only annular-like (transverse) waves propagating directly from the source appear, but hybrid internal waves propagating upstream from the source are also generated. In this case, there is an upstream wave front which is indicated by the dotted line in Figure 4. The dashed line in Figure 4 is the crest of the wave with phase $\Phi=0$, the phase of the annular crests and the longitudinal crests to the left of the dashed line in Figure 4 is $\Phi>0$, and the phase of the longitudinal crests to the right of the dashed line is $\Phi<0$. Figure 6, Figure 7, Figure 8, and Figure 9 show the phase structure and the wave pattern corresponding to the lower branch of the dispersion curve for the third and fourth intervals.
We describe the qualitative evolution of the wave patterns of the excited fields (corresponding to the lower branches of the dispersion curves) depending on the frequency $\omega$ of the perturbation source oscillations. At $0< \omega < \omega_1$, the wave pattern consists of waves of the following two types: wedge-like (longitudinal) and annular-like (transverse); in this case, the annular-like (transverse) waves propagate directly from the perturbation source, including the upstream direction. At $ \omega_1 < \omega < \omega_2$, the lower and closed branches of the dispersion curves merge and form a unique $\Omega$-like curve. In this case, the half-opening angle of the wave wedge in the wave pattern is greater than $\pi/2$, and the wave pattern is a system of hybrid waves, i.e., the properties of the waves correspond both to the annular-like (transverse) and wedge-like (longitudinal) waves. At $ \omega_2 < \omega < 1$, the lower branch of the dispersion curve becomes a single-valued function intersecting the abscissa axis, the half-opening angle of the wave wedge is less than $\pi/2$, and the wave pattern contains only wedge-like (longitudinal) waves. At $ \omega_2 < \omega < 1$, the lower branch of the dispersion curve is completely in the upper half-plane and the corresponding phase structure consists of curvilinear triangles embedded in the wave wedge so that their bases face the origin. At $ \omega_2 < \omega < 1$, the vertices of the triangles embedded in the wave wedge face the origin. In the generation intervals $ \omega_2 < \omega < 1$ the wave pattern consists only of a system of wedge-like (longitudinal) waves.
Thus, the results of mathematical simulation of unsteady generation regimes show that, at certain generation regimes, the fields of internal gravity waves excited by an unsteady source moving in the stratified ocean of a finite depth present a hybrid system of waves of the following two types: annular-like (transverse) and wedge-like (longitudinal). Since the perturbation source is unsteady, not only annular-like wave propagating directly from the source appears, but hybrid internal waves propagating upstream from the source are also generated.
The qualitative pattern of wave fields at a far distance from the pulsing perturbation source is significantly more complicated compared to the case of wave generation by a moving stationary perturbation source, when the wave fronts of separate modes, starting from the first, successively arrive to a fixed observation point. First, at some parameters of the source motion (velocity, pulsation frequency), the annular waves can first arrive to the fixed observation point, and the number of arriving waves is always finite. Second, unlike the case of internal gravity wave generation by a stationary perturbation source, the front of the wave mode other than the first mode but with the greatest half-opening angle of the Kelvin wedge can first arrive at the observation point before the front of the first mode, then the front of the second mode arrives, and so on in succession. The number of the wave mode which is the first to arrive to the fixed observation point depends on the velocity of the perturbation source motion, the frequency of its pulsation, and the Brunt-Väisälä frequency. The number of wedge-like wave modes with the half-opening angle of the Kelvin wedge greater than the half-opening angle of the Kelvin wedge of the first mode is finite. At large numbers of modes, the half-opening angle of the Kelvin wave wedge decreases with the number of the mode similarly to the case of internal wave generation by a stationary perturbation source.
The results of the mathematical simulation of internal gravity wave fields allow us to efficiently analyze the main amplitude-phase characteristics of the excited wave fields and, in addition, a qualitative investigation of the obtained solutions is possible, which is important for the express estimation of the wave field characteristics in full-scale observations in the ocean and for the well-posed statement of more complicated mathematical models of the wave dynamics of real stratified media. In conclusion, we note that similar wave patterns can be observed in remote sensing, observation, and measurements of internal gravity waves excited by various perturbation sources in the natural (ocean, the Earth atmosphere) and artificially stratified media.
Abdilghanie, A. M., P. J. Diamessis (2013), The internal gravity wave field emitted by a stably stratified turbulent wake, J. Fluid Mech., 720, p. 104–139, https://doi.org/10.1017/jfm.2012.640.
Bulatov, V. V., Yu. V. Vladimirov (2012), Wave Dynamics of Stratified Mediums, 584 pp., Nauka, Moscow.
Bulatov, V. V., Yu. V. Vladimirov (2015a), Volni v Stratifitsirovannikh Sredakh, 735 pp., Nauka, Moscow (in Russian).
Bulatov, V. V., Yu. V. Vladimirov (2015b), Internal gravity waves excited by a pulsating source of perturbations, Fluid Dynamics, 50, no. 6, p. 741–747, https://doi.org/10.1134/S0015462815060034.
Massel, S. R. (2015), Internal Gravity Waves in the Shallow Seas, 163 pp., Springer, Berlin.
Mei, C. C., M. Stiassnie, D. K.-P. Yue (2017), Theory and applications of ocean surface waves. Advanced series of ocean engineering. V. 42, 1500 pp., World Scientific Publishing, London.
Morozov, E. G. (1995), Semidiurnal internal wave global field, Deep Sea Res., 42, no. 1, p. 135–148, https://doi.org/10.1016/0967-0637(95)92886-C.
Morozov, E. G. (2018), Oceanic Internal Tides. Observations, Analysis, and Modeling, 317 pp., Springer, Berlin.
Navrotsky, V. V., V. Yu. Liapidevskii, E. P. Pavlova (2013), Features of internal waves in a shoaling thermocline, Int. J. Geosciences, 4, p. 871–879, https://doi.org/10.4236/ijg.2013.45081.
Pedlosky, J. (2010), Waves in the Ocean and Atmosphere: Introduction to Wave Dynamics, 260 pp., Springer, Berlin.
Pisarev, S. V. (1996), Low-frequency internal waves near the shelf edge of the Arctic Basin, Oceanology, 36, no. 6, p. 771–778.
Rees, T., K. G. Lamb, F. J. Poulin (2012), Asymptotic analysis of the forces internal gravity waves equation, SIAM J. Appl. Math., 72, no. 4, p. 1041–1060, https://doi.org/10.1137/110842892.
Sutherland, B. R. (2010), Internal Gravity Waves, 394 pp., Cambridge University Press, Cambridge.
Tiugin, D. Iu., A. A. Kurkin, E. N. Pelinovskij, O. E. Kurkina (2012), Povishenie proizvoditelnosti programnogo kompleksa dlia modelorovaniia vnutrennikh gravitatsionikh voln IGW Research s pomoshchiu Intel Parallel Studio XE 2013, Fundamentalnaia i Prikladnaia Gidrofizika, 5, no. 3, p. 89–95 (in Russian).
Vlasenko, V., N. Stashchuk, K. Hutter (2005), Baroclinic Tides, 372 pp., Cambridge University Press, NY, https://doi.org/10.1017/CBO9780511535932.
Received 26 February 2018; accepted 6 March 2018; published 24 April 2018.


Citation: Bulatov V. V., Yu. V. Vladimirov (2018), Unsteady regimes of internal gravity wave generation in the ocean, Russ. J. Earth Sci., 18, ES2004, doi:10.2205/2018ES000619.
Copyright 2018 by the Geophysical Center RAS.