RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 17, ES2002, doi:10.2205/2017ES000597, 2017
V. A. Pilipenko1,2, O. V. Kozyreva2,3, M. J. Engebretson4, A. A. Soloviev1,3
1Geophysical Center, Russian Academy of Sciences, Moscow, Russia
2Space Research Institute, Russian Academy of Sciences, Moscow, Russia
3Schmidt Institute of Physics of the Earth, Russian Academy of Sciences, Moscow, Russia
4Augsburg College, Minneapolis, USA
A ULF wave index, characterizing the level of the geomagnetic field variability in the frequency range 2–7 mHz, has been suggested to the space physics and geophysical community. This global wave index is produced from all available arrays of magnetometers and isolated stations in the Northern hemisphere. A similar ULF wave index is calculated using magnetometer data from geostationary (GOES) and interplanetary (Wind, ACE) satellites. In this review we demonstrate that a wide range of space physics studies, such as the solar wind-ionosphere coupling, wave energy transport, substorm physics, relativistic electron energization, ring current formation, electrodynamics of the ionosphere and magnetosphere, search for electromagnetic precursors of earthquakes, etc., has benefited from the introduction of the provisional ULF wave index. Possible ways of the ULF index advancement and development are discussed. The permanently updating ULF-index database is freely available via the website ulf.gcras.ru for all interested researchers for further validation and statistical studies.
The interaction between the solar wind (SW) and terrestrial magnetosphere is the primary driver of many of the processes and phenomena occurring in the near-Earth environment. This interaction has often been viewed using the implicit assumption of quasi-steady interplanetary magnetic field (IMF) and laminar plasma flow. However, new conceptions of the magnetospheric plasma dynamics are being developed, in which turbulence plays a fundamental role [Borovsky et al., 1997]. Progress in understanding and monitoring these turbulent processes in space physics is hampered by the lack of convenient tools for their characterization.
Various geomagnetic indices ($Kp$, $AE$, $Dst$, $SYM$-$H$, $PC$, etc.) and averaged SW/IMF parameters quantify the energy supply in certain regions of the magnetosphere–ionosphere system, and are used as primary tools in statistical studies of solar-terrestrial relationships. However, these indices characterize the steady-state level of the electrodynamics of the near-Earth environment. The turbulent character of SW drivers and the existence of natural MHD waveguides and resonators in the magnetospheric plasma in the ultra low-frequency (ULF) frequency range ($\sim 2-10$ mHz) ensures a quasi-periodic response to forcing at the boundary layers. Therefore, much of the turbulent nature of SW-magnetosphere-ionosphere interactions can be monitored with ground-based or space observations in the ULF frequency range. The new "ULF wave power index", showing the turbulent character of the energy transfer from the SW into the upper atmosphere and the short-scale variability of near-Earth electromagnetic processes has been suggested by Kozyreva et al. [2007]. Even provisional version of this index has been successfully used in various areas of space physics. Here we briefly review these results and outline possible directions of the index advancement.
An hourly ULF wave index, using the spectral features of ULF power in the Pc5 band (periods from $\sim 500$ s to $\sim 150$ s) is derived from a global array of stations in the Northern hemisphere [Kozyreva and Kleimenova, 2008, 2009, 2010; Kozyreva et al., 2007]. Data from the following global magnetometer arrays with 1-min time sampling are used:
 |
| Figure 1 |
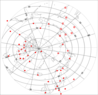
A map with station locations is shown in Figure 1. Though the existing database of the magnetometer data is already suitable for the index construction, it is possible to augment the database with additional stations, such as CARISMA (www.carisma.ca), IMAGE (www.geo.fmi.fi/image), Greenland Coastal Array (www.space.dtu.dk), GIMA (www.asf.alaska.edu/program/gdc/project/magnetometer).
The data have been detrended with a cut-off frequency 0.5 mHz and converted into a geocentric ($X,Y$) coordinate system. For any UT hour, the magnetic stations in a chosen $LT$ sector (from $LT1$ to $LT2$), and in a selected CGM latitude range (from $\Phi_{\mathrm{S}}$ to $\Phi_{\mathrm{N}}$) are selected. The amplitude spectra $F(f)$ of each horizontal component are calculated with the use of Filon's integration method in a 1 hour time running window.
 |
| Figure 2 |
The signal and background noise spectral contents are estimated in the following way. In a log-linear plot of $F(f)$ the linear fit $LF(f)$ is applied, which fits to a linear model by minimizing the chi-square error $\sigma$, in the frequency band from $f_1$ to $f_2$. Then, a discrimination line, separating the background noise $F_B(f)$ and signal spectra, is considered as $\log F_B (f) = LF(f) - \sigma$ (as schematically illustrated in Figure 2). A spectral bump above the discrimination line is considered as a contribution from a narrow-band signal.
The frequency range selected for construction of the ULF index is bounded by the lower and upper frequencies $f_L$ and $f_H$. Noise spectral band-integrated in the range $\Delta f = f_H - f_L$ power $N_j$ is calculated at each $j$-th station as the area beneath the discrimination level
\begin{eqnarray*} N_j = (\Delta f)^{-1} \int_{f_L}^{f_H} F_B (f) df \end{eqnarray*}Signal spectral power $S$ is the area of the bump above the background spectrum $F_B(f)$, that is
\begin{eqnarray*} S_j = (\Delta f)^{-1} \int_{f_L}^{f_H} \{ F(f) - F_B (f)\} df \end{eqnarray*}The ULF wave indices, comprising total power $T_j$ and signal power $S_j$, are calculated from the band-integrated spectral power at station a maximal amplitude. The index has been normalized by the spectral width to make the index dimension [nT].
The following parameters have been used for the calculation of the provisional version of ground ULF index. The magnetic stations have been selected from $LT1=05$ to $LT2=15$, and in a CGM latitude range from $\Phi_{\mathrm{S}}=60\mbox{°}$ to $\Phi_{\mathrm{N}}=75\mbox{°}$. The selection of limited $LT$ sector has been made to suppress a contribution of nighttime substorm activity into the index. The frequency range is from $f_L=2.0$ mHz to $f_H=7.0$ mHz, and the discrimination level was estimated by a linear fit in the frequency interval $f_1=1$ mHz to $f_2=8$ mHz. The Nyquist frequency for a 1-min sampling period is 8.3 mHz.
Ground magnetic fluctuations are not always a perfect proxy of the ULF fluctuations in the magnetosphere. In particular, there is a class of ULF waves – storm-related poloidal Alfven waves, that occur at the recovery phase of magnetic storm in the dusk/noon sectors of the magnetosphere. These ULF waves are generated by the ring current protons via various kinds of drift instabilities [Pilipenko, 1990]. Despite their high amplitudes in the magnetosphere, these pulsations are rarely if ever seen on the ground because of their small azimuthal scales, that cause effective screening by the ionosphere. Thus, the ground global index needs to be augmented by a similar index, estimated from space magnetometer data. This wave index, coined the GEO ULF-index, is calculated from 1-min 3-component magnetic data from the geostationary GOES satellites to quantify the short-term magnetic variability in the region of geostationary orbit. No selection in $LT$ has been applied to GEO index. The GEO index is the sum of spectral power of all 3 components.
To quantify the short-term variability of IMF and SW plasma, the interplanetary ULF indices are estimated using 1-min data from the interplanetary satellites Wind, ACE, and IMP8, compiled into the OMNI database. The data from these satellites are time-shifted to account for the propagation from the satellite location towards the magnetopause.
The hardest part of the index production is the compilation of uniform database from all available ground and space flux-gate magnetometers, reading data in various formats, etc. This pre-processing demands a lot of manpower, because even INTERMAGNET data are not 100% perfect. The pre-processing includes the manual elimination of spikes, level jumps, interference, and short data gaps. The database compiled for the index production is more complete than the database collected in the largest world system SuperMAG (supermag.jhuapl.edu) for the accumulation and dissemination of magnetometer data.
The hourly ULF index database has been compiled for the period since 1991 up to nowadays, and is permanently updating. The database is freely available via the specially designed website ulf.gcras.ru/. The website provides a user the possibility:
Additionally, the website provides a list of downloadable journal publications and conference reports related to the use of ULF wave index in space weather studies. Description of the IDL computer algorithm used upon the index production is given also. Researchers interested in statistical studies with the use of ULF index can get access via FTP to zip-compressed monthly files. It is possible to submit a request for the index calculation with non-standard parameters or for a specific region.
A wide range of space physics studies already benefited from the introduction this new index. Some of them are reviewed below.
The appearance of relativistic electrons in the outer radiation belt following some geomagnetic storms resists definitive explanation in spite of many years of study. These electron events (called "killer" electrons) are not merely a curiosity for scientists, but they can have disruptive consequences for spacecraft [Pilipenko et al., 2006]. While it has been known that there is a general association between geomagnetic storms and electron enhancements [Reeves, 1998], the wide variability of the observed response and the puzzling time delay ($\sim 1-2$ days) between storm main phase and the peak of the response has frustrated the identification of responsible mechanisms and controlling parameters. Ultimately, the SW is the energy resource for geomagnetic storms in general and acceleration of electrons to relativistic energies. The acceleration mechanisms require seed electrons of a few hundred keV which are usually supplied by substorms. However, since the SW does not directly contact the electrons in question, some magnetospheric intermediary must more directly provide the energy to the electrons. ULF waves in the Pc5 band have emerged as a possible energy reservoir, because in a laminar, non-turbulent magnetosphere the "killer" electrons would not appear [Potapov et al., 2014; Rostoker et al., 1998; Shprits et al., 2008a].
The observations showed that the enhancements in electron energies (beyond levels expected from conserving adiabatic invariants) at geosynchronous orbit occur rapidly within a few hours at the onset of a magnetic storm, but there is also a slower additional acceleration that peak fluxes are seen after a number of days [Li et al., 2001].
Observations of relativistic electron response to magnetic storms showed an inadequacy of the traditional radial diffusion-based energization mechanism owing to irregular magnetic pulses [Tverskoi, 1968]. This led to proposals for a more efficient energization mechanism based on resonant interaction of drifting electrons with coherent MHD oscillations in the Pc5 frequency range [Elkington et al., 1999; Hudson et al., 2000 Liu et al., 1999]. This drift-resonance mechanism is in fact a revival of the old idea of a magnetospheric "geosynchrotron" [Pokhotelov et al., 1999]. Pumping of energy into seed $\sim 100$ keV electrons is provided by large-scale MHD waves in a resonant way, when the wave period matches the multiple of the electron drift period, e.g. $\omega=m \omega_d$.
There have been some observations that favor the idea of ULF wave-related acceleration of magnetospheric electrons. The wave power in the Pc5 band at a ground station rapidly increased less than an hour before the appearance of relativistic electrons, prompting Baker et al. [1998] to suggest that Pc5 pulsations were an acceleration mechanism for these electrons. The use of one station only is evidently insufficient to validate the role of global ULF wave activity in energizing magnetospheric electrons. There was better observational support for a ULF contribution to the later, slower energization of electrons. O'Brien et al. [2001] performed a superposed epoch analysis to compare storms with and without the appearance of hourly electron fluxes ($>2$ MeV) at GOES and LANL geosynchronous monitors. Long duration elevated Pc5 ULF wave power during the recovery phase appeared to discriminate better than $Dst$ or $AE$ between those storms that do and do not produce relativistic electrons showed that electron events had a higher ULF power at some mid-latitude stations by about an order of magnitude in the recovery phase [Mann et al., 2004; Mathie and Mann, 2001]. Main phase intensity did not appear to be an important indicator of subsequent electron behavior. A more convincing statistical evaluation of possible coupling between ULF activity and relativistic electron dynamics demands a quantitative measure to characterize global ULF wave behavior. The introduced ULF wave index became a convenient tool in a correlative statistical studies with the relativistic electron dynamics.
The analysis of the period with disturbed space weather has shown that sustained intense increases of GOES-8 relativistic electrons fluxes occurred after weak and moderate storms ($|Dst|<100$ nT) driven by high-speed SW streams, whereas the increase after strong storms ($|Dst|>200$ nT) was much shorter and less intense [Romanova and Pilipenko, 2008]. The electron behavior matched well the variations of the global ground ULF-index: after weak storms this index increased much more substantially and for a longer period than after strong storms. These studies demonstrated the usefulness and ease of use of the ULF wave index for studies of high-energy particle energization in the magnetosphere.
However, the drift resonant interaction with ULF waves is not the only mechanism of relativistic electron acceleration. VLF waves may be associated both with increases in flux due to acceleration of electrons by chorus waves and decreases due to precipitation caused by hiss. Modern theories and observational evidences are summarized in reviews [Shprits et al., 2008b].
An easy availability and ease of use of single parameter characterizing ULF wave activity in various domains of the outer space greatly facilitates the statistical studies. Long-period ground ULF wave activity in the Pc5 range is controlled by the SW/IMF parameters. Simms et al. [2010] investigated the influence of these parameters on ground Pc5 activity using ULF wave power index as a proxy during quiet and storm periods. With multiple regression and path analysis, they studied the influence of these parameters as a set rather than individually. This allowed one to determine which factors were most influential and which were only correlated with influential factors. By using multiple regression, more variation in Pc5 power was explained than has been achieved in previous studies. In both storm types, driven either by the coronal mass ejection or corotating interaction region, and during all storm phases as well as during quiet periods, SW velocity and IMF $Bz$ influenced ground Pc5 power directly. These two variables also acted on the Pc5 power indirectly through the intermediate parameters of $Dst$, and the variations in SW density and IMF. Ground Pc5 power was greater during CME storms during the main phase, but larger during CIR storms in the recovery period. A statistical model such as this offers the possibility of nowcasting Pc5 power by inserting current levels of SW/IMF variables as predictors into the regression equation [Pilipenko et al., 2008].
One of the key problem of space physics is a reliable prediction of the relativistic electron fluxes in the magnetosphere. The daily maximum relativistic electron flux $J$ at geostationary orbit was attempted to predict with a set of variables including previous day's flux $J_{-1}$, seed electron ($\sim 100$ keV) flux, SW velocity and density, $AE$ index, IMF $Bz$, $Dst$, and ground ULF and VLF wave power [Simms et al., 2014]. As predictor variables are intercorrelated, used multiple regression analyses to determine which are the most predictive of flux when other variables are controlled. Mathematically, the predicted response variable $J$ is a linear combination of the prediction parameters $X_i$ multiplied by their regression coefficients $b_i$:
\begin{eqnarray*} J_i = b_0 + \sum_{i=1}^{i=N} b_i X_i \end{eqnarray*}Empirical model produced from regressions of $J$ on measured predictors from one day previous was reasonably effective at predicting novel observations. Adding previous flux $J_{-1}$ to the parameter set improved the prediction of the amplitude of the increase, but delayed its anticipation of an event. Previous day's SW density and velocity, $AE$ index, and ULF power index were the most significant explanatory variables. The AE index showed a negative correlation with $J$ when other parameters are controlled, that may be due to the triggering of electromagnetic ion cyclotron waves by substorms that cause electron precipitation.
VLF waves showed lower, but significant, influence. The combined effect of ULF and VLF waves shows a synergistic interaction, where each increases the influence of the other on flux enhancement. Correlations between observations and predictions for this one-day lag model ranged about 0.8. Probably, the magnetospheric electrons are most effectively accelerated owing to the radial diffusion and preliminary energization under the influence of ULF waves, and subsequent local acceleration by VLF chorus electromagnetic emissions.
 |
| Figure 3 |
Many SW and magnetosphere parameters, as well as ULF waves, could be used to predict relativistic electron flux levels at geostationary orbit following storms using a data-based model produced by multiple regression. As many of these factors are correlated among themselves, Simms et al. [2014] developed model that attempted to determine which of these factors correlated with and predicted flux best. However, Simms et al. [2014] using ground-based measurements of VLF magnetospheric emissions showed little ability to predict enhanced relativistic electron flux. A daily average of VLF wave power from the ground instrument, which picks up both chorus and hiss, may result in a measure that cannot distinguish between the opposing effects of acceleration and precipitation. Therefore, Simms et al. [2015] compared the daily average with VLF averaged from Halley station only over the dawn period when chorus dominates (0600–0900 MLT). They used the 1.0 kHz channel of Halley VLF instrument, which detects VLF from $L<7.5$, including those at geosynchronous orbit. A nowcast model gave only a moderate correlation $\sim 0.35$ between predicted and observed $J$. A model using predictors from the previous day gives similar correlations $\sim 0.4$. Adding the previous day's flux $J_{-1}$ to this model improved the correlation to $\sim 0.8$. A time plot of these observed and predicted values shows how well predictions track flux levels during the third quarter of 1998 (Figure 3). The observed values (solid line) are well predicted by the one-day lag model that includes lagged flux (dashed line). The one-day lag model without flux underestimates the height of some peaks and overestimates others (dotted line). Both statistical models are able to predict increases of relativistic electron fluxes at geosynchronous orbit and can be used in space weather centers.
The level of upstream SW turbulence determines the turbulent viscosity of the flow passing the magnetosphere, and as a result, the degree of coupling of the SW to the magnetosphere appears to be influenced by the level of turbulence upstream of the Earth. There are indications that the magnetosphere indeed is driven more weakly, especially for northward IMF, when the level of SW turbulence is low [Borovsky and Funsten, 2003]. Thus, the magnetosphere behaves as a turbulent high-Reynolds-number system, and the presence of turbulence in the flows inside and outside the magnetosphere should have profound effects on its large-scale dynamics through eddy viscosity and diffusion.
The turbulent/eddy viscosity of the SW flow passing the magnetosphere is controlled to a considerable extent by the level of upstream turbulence. Though, the turbulence level of the magnetosheath plasma, which directly interacts with the magnetosphere, can differ significantly for different IMF orientation in respect to the bow shock, the degree of coupling of the SW flow to the magnetosphere appears to be influenced by the level of SW/IMF turbulence upstream of the Earth. The turbulent viscosity concept predicts that the coupling to be lessened when the level of upstream turbulence is low. Therefore, the presence of turbulence inside and outside the magnetosphere should have profound effects on the large-scale dynamics of the system through viscosity and diffusion.
 |
| Figure 4 |
Using the ULF index of the IMF variability SIMF, Romanova and Pilipenko [2008] verified the fact that when the IMF is more turbulent, the effective degree of its coupling to magnetosphere is higher. The IMF was considered as noisy when log $S_{\mathrm{IMF}}>0$, and IMF was calm when log $S_{\mathrm{IMF}}<0$. Auroral response, as characterized by hourly $AE$ index, was compared in Figure 4 with a strength of the SW driver, determined by the IMF $Bz$ component, for the calm (blue dots) and turbulent (red dots) IMF for the period 1994–1995. Comparison of median curves shows that under southward IMF ($Bz<0$) $AE$ nearly linear grows upon increase of the magnitude of $Bz$, whereas the average $AE$ response to the turbulent IMF is higher. This difference is significant not only for northward IMF, when one expects the viscous interaction to be dominant over the reconnection, but it reveals itself even under southward IMF. This comparison confirms that the magnetosphere is driven more strongly when the IMF turbulence level is elevated.
ULF wave power in the SW was proposed to be an additional factor in controlling the coupling of the SW–magnetosphere–ionosphere system. Kim et al. [2009] and Lyons et al. [2009] showed that enhanced ULF wave power can substantially enhance the convection strength in both the dayside and nightside high latitude ionosphere. This ULF power effect was found to be independent of an observed direct effect from the SW speed. Lyons et al. [2009] showed some examples of an increase of plasma sheet pressure and substorm occurrence rate during periods of strong ULF wave activity under northward IMF, indicating that ULF wave activity may play an important role in substorm triggering.
 |
| Figure 5 |
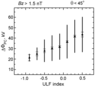
ULF fluctuations may also be an important contributor to the coupling of the SW to the magnetosphere-ionosphere system. Regardless of the IMF orientation, ULF fluctuations in the SW can substantially enhance the convection in the high latitude ionosphere [Kim et al., 2011]. They conducted a statistical study to understand the effect of ULF power in the IMF on the cross polar cap potential $\Delta \Phi_{pc}$. The average $\Delta \Phi_{pc}$ showed a roughly linear dependence on the ULF power index TIMF (Figure 5). Highly structured convection flow patterns were often observed under fluctuating northward IMF. For such a convection configuration, it is hard to estimate properly the cross polar cap potential drop, as the enhanced flows around the vortices that may be associated with IMF fluctuations do not necessarily yield a large potential drop. Thus, despite the relatively small correlation coefficient, the linear trend gives support to the significant role of IMF fluctuations on the coupling of the SW to the magnetosphere-ionosphere system. They also examined the isolated effect of IMF ULF power by comparing two data sets that are associated with a lower and a higher ULF power level but satisfy the same SW conditions. They observed a substantially greater number of large polar cap potentials for the data set associated with a higher ULF power, which further supports there being a substantial effect of IMF ULF power on $\Delta \Phi_{pc}$.
Borovsky and Denton [2014] explored the ULF ower index and incorporated it into a composite Earth variable composed of multiple geomagnetic indices plus the ground-based and geosynchronous ULF indices. Correlations between the ULF indices and the SW, between the ULF indices and SW driver functions for the magnetosphere, and between the ULF indices and relativistic-electron fluxes were explored. To examine the driving of the ULF indices by the SW and to investigate the connections of the ULF indices to other geomagnetic indices, the mathematical technique of canonical correlation analysis was utilized.
There are currently two contrasting views on the ring current formation during magnetic storms. The conventional idea is that the ring current results from the accumulation of particles injected during substorms. Another view asserts that ring current development results from a sustained enhancement of the convection electric field driven by the IMF/SW. A large body of work has demonstrated that it is the SW that injects the particles that create the ring current. In this view it is implicitly assumed that there must be some secondary process that scatters particles from open to closed drift paths. The process must be relatively efficient and continuous, otherwise the injection rate would not depend so strongly on the SW electric field. McPherron [1997] suggested that this process is a combination of inherent fluctuations in the SW electric fields, waves in the magnetosphere, and inductive electric fields caused by a substorm expansion phase. This process, though being of key importance, is not observable in any existing indices. The necessity to use the set of existing indices for the selection of this problem is evident.
The variability of SW and magnetospheric conditions might be an important factor in triggering magnetospheric substorms [Kamide, 2001]. Although there is a modest amount of theoretical and observational evidence supporting this view, this idea has not been thoroughly examined by the space community so far, and it is not used for space weather purposes. Enhanced reconnection and viscous interaction in dayside boundary regions, leading eventually to substorms, most probably are accompanied by an enhanced level of turbulence. Therefore, substorm break-ups may be preceded by an increased level of ULF power in the region of the dayside boundary layers [Pilipenko et al., 1998]. Also, the pre-heating of the nightside plasmasheet plasma owing to the resonant absorption of MHD turbulence may provide necessary conditions for the onset of an explosive instability, resulting in a substorm break-up (the so called "thermal catastrophe" model of Goertz and Smith [1989]). Samson et al. [1992] identified a number of intervals in which auroral intensifications occurred during times when nighttime field line resonances occurred, indicating that ULF waves may play a role in triggering substorm intensifications. A statistical study of low-frequency magnetic activity in the night side region of the poleward auroral boundary revealed an enhancement of ULF power about 2–3 hours before the explosive phase of substorms [Yagova et al., 2000]. Further application of reliable statistical methods for the search for wave precursors of substorms will benefit from the development of a database containing an index quantifying ULF activity. It will be particularly interesting to reveal that the fluctuations associated with energy transfer to the magnetosphere can to lead to the growth and expansion phase of substorms under conditions when such energy transfer would not otherwise be expected.
The interplanetary ULF wave power index can be used as a simple and convenient tool for the statistical examination of the SW and IMF turbulence. The SW density fluctuations with time scales $\sim 2-250$ min were examined statistically, using a modification of ULF wave indices [Romanova et al., 2007]. As a measure of ULF density fluctuations the integrated wavelet power $W_n$ from 4 min to 128 min was used. To examine the change of the SW turbulence before magnetic storm onsets the interplanetary ULF wave index $W_{\mathrm{N}}$ chracterizing the SW density fluctuations was used. The statistical histograms of $W_n$ distributions during the entire year and during 12 hours intervals before storm onsets revealed a shift of the distribution to higher values before storms during both solar minimum (2000) and maximum (1995). Thus, the SW density becomes more turbulent and irregular about 12 hours before the arrival of solar streams causing storms, especially during the solar maximum.
The mechanism of this effect has not been found yet, and may be related to the following consideration. The plasma density enhancements are observed near the heliospheric current sheet (HCS) and high-speed corotating streams adjacent to it. Thus, a high irregular plasma density may be an indicator that Earth is approaching the HCS owing to the presence of naturally occurring high densities near the HCS and stream-stream compressive effects. The southward IMF, which eventually causes moderate storms, is related to the corotating stream interaction with the HCS and its plasma sheet. Although corotating stream/HCS plasma sheet interaction can create intense southward IMF, though highly fluctuating. Thus, the statistical result above may reflect the fact that the HCS is a region favorable for the moderate magnetic storm occurrence.
Although the proposed ULF wave index is more suited for solar-terrestrial studies, its introduction might be of significant help to the community developing electromagnetic methods of earthquake prediction. Anomalous ULF noise may occur a few days-weeks before strong earthquakes [Hattori, 2004; Molchanov and Hayakawa, 2008]. This effect may be caused by various mechano-electromagnetic conversion processes in the crust at the final stage of the seismic preparatory phase [Surkov and Pilipenko, 1999]. Validation of this effect on a large statistical basis with the use of magnetic stations in seismo-active regions will be possible only with the use of a proper ULF wave index. This index will provide the seismic community with an effective tool to distinguish local seismo-related electromagnetic anomalies from global enhancements of ULF wave activity of the space origin. The search for earthquake precursor signatures in ULF magnetic records has often involved the spectral power of Pc3–5 variations. While possible precursor signatures have been reported, some have disputed the results, pointing to contributions from near-Earth space processes. Geomagnetic indices have been used in an attempt to distinguish between possible seismic and near-Earth space sources of ULF power, implicitly assuming that the relationship between ULF power and the geomagnetic indices. Using CARISMA magnetometer data, Currie and Waters [2014] have shown that the relationships between ULF power integrated over the Pc3–5 bands with $Kp$, $SYM$-$H$, and $Dst$ vary with magnetic latitude and local time, but most correlation coefficient values are small, near 0.2. Therefore, these indices are not satisfactory predictors of Pc3–5 activity. Therefore, widely used by seismic prediction community geomagnetic indices are not effective for the discrimination of magnetospheric and lithospheric emissions, and they should be replaced by the ULF wave power index for a relevant latitudes.
The provisional ULF wave power index has some drawbacks and deficiencies. The current research is aimed to overcome them and suggest a more effective and robust index.
The usage of a wave index based on band-integrated wave power only may be insufficient, because this type of index cannot discriminate between irregular wideband variations and narrowband waves. For example, Posch et al. [2003] applied to the analysis of ULF dynamics during storms a simple measure $R$ of the fraction of narrow-band pulsations in observed wave power. The $R$ parameter is calculated as the ratio between the wave power in a narrow band (2–10 mHz) and wide band (0.2–10 mHz). The ULF activity during the main phase was in fact broadband ($R$ is low). This broadband wave activity is caused by other mechanisms than typical Pc5 waves, and their features (spectrum, transverse spatial scale) differ from ULF waves at the storm recovery phase. The ULF activity in the recovery phase was narrowband in the dawn-to-noon $LT$ sector ($R$ is high). Thus, for the discrimination of broad-band and narrow-band variations an algorithm, based on the ratio $T_{\mathrm{narrow}}/T_{\mathrm{wide}}$ between the wave power in a narrow band $T_{\mathrm{narrow}}$ and wide band $T_{\mathrm{wide}}$, can be applied. So far, to discriminate between broadband and narrowband ULF waves the ratio between signal and total powers $R=S/T$ can be used.
Using a similar approach, ULF index can be constructed in other ULF frequency bands, using data from world-wide array of ground instruments.
ULF waves in the Pc3 band (10–100 mHz) observed on the ground are closely related to the upstream turbulence in the terrestrial foreshock region. Therefore, a measure of ground Pc3 wave power could be a useful Pc3 index, characterizing the intensity of upstream turbulence [Heilig et al., 2010]. Additionally, the Pc3 central frequency enables one to determine the IMF magnitude.
Electromagnetic ion-cyclotron waves in the Pc1 band (0.1–5 Hz) are beleived to be responsible for depleting the outer radiation belt by causing the pitch-angle diffusion and precipitation of relativistic electrons. Understanding the outer radiation belt dynamics requires an index to characterize the global intensity of Pc1 waves. For that a belt of induction magnetometers at middle latitudes should be composed.
The resonant interaction with ULF waves is not the only mechanism of relativistic electron acceleration, and VLF emissions may be responsible for local increases in flux due to acceleration of electrons by chorus emissions and decreases due to precipitation caused by hiss emissions. Therefore, the construction of statistical models for nowcasting and predicting relativistic electron fluxes demands an index, characterizing VLF wave power. However, daily average of VLF wave power from the ground instrument, which in fact picks up both chorus and hiss, may result in a measure that cannot distinguish between the opposing effects of acceleration and precipitation [Simms et al., 2016] As a first step, a daily parameter with VLF power averaged from ground stations, but this averaging must be performed only over the dawn period (0600–0900 MLT) when chorus dominates. For that the channel around 1.0 kHz of ground VLF instrument, which detects VLF emissions from a range of latitudes, covering the geosynchronous orbit, is to be used.
The ULF indices show some deficiencies that are probably related to the presence of nonsinusoidal UT periodic variations. Temporal autocorrelation functions of the ULF indices were examined and compared with autocorrelation functions of various SW and geomagnetic quantities by Borovsky and Denton [2014]. The local peaks in the autocorrelation functions at multiples of 24 h were found, which indicate the presence in the time series of a non-sinusoidal variations with a 24 h period. The origin of these variations may be caused by very uneven globe coverage with magnetic stations. Removal of the 24 h and 12 h periodic variations would undoubtedly make the ULF indices more predictable and should boost their contribution to the Earth data set.
Detrended ULF indices can be produced by subtracting off UT sine wave functions. These functions $\bar{S}_{\mathrm{gr}}$ and $\bar{S}_{\mathrm{geo}}$ were determined by Borovsky and Denton [2014] by regression fitting the entire 1991–2004 databases as follows
\begin{eqnarray*} \bar{S}_{\mathrm{gr}} = S_{\mathrm{gr}} - 1.065 - 0.07957 \sin (2 \pi [\mathrm{UT} + 16.784] \bigl/ 24) \end{eqnarray*} \begin{eqnarray*} \bar{S}_{\mathrm{geo}} = S_{\mathrm{geo}} + 0.1415 + 0.07563 \sin (2 \pi [\mathrm{UT} + 5.676] \bigl/ 24) \end{eqnarray*}and the detrended indices $\bar{T}_{\mathrm{gr}}$ and $\bar{T}_{\mathrm{geo}}$ are given by
\begin{eqnarray*} \bar{T}_{\mathrm{gr}} = T_{\mathrm{gr}} - 0.87889 - 0.08391 \sin (2 \pi [\mathrm{UT} + 16.097] \bigl/ 24) \end{eqnarray*} \begin{eqnarray*} \bar{T}_{\mathrm{geo}} = T_{\mathrm{geo}} + 0.3732 - 0.07292 \sin (2 \pi [\mathrm{UT} + 6.072] \bigl/ 24) \end{eqnarray*}where the UT is given in hours. A straightforward correction to indices would be to subtract off the UT-dependent means from the data.
A next step would be to consider renormalizing the distribution of values at each UT so that all UT bins have the same standard deviations and skewnesses. The ?rst correction will undoubtedly improve the correlations of ULF indices with SW parameters and with other geomagnetic indices. One might also consider performing these renormalizations separately for each of the GOES spacecraft used to construct the geosynchronous ULF index.
Fitting those 24 h variations and subtracting them out would produce ground-based and geosynchronous ULF indices with less noise and higher correlations with SW parameters and with other geomagnetic indices. Those improved ULF indices will also better correlate with the relativistic-electron flux in the magnetosphere.
Construction of the ULF index demands the processing of all available database from a wide array of stations as a whole. Elaboration of such models is hampered by the lack of effective and flexible tools for automatic selection of characteristic features of phenomenon under study – monochromatic signals, wideband noise, impulses with given waveforms, etc. Widely used so far estimates of the spectral power density are insufficient for the wave discrimination. Probabilistic methods of a signal detection, frequency-time analysis, wavelet-analysis and neural networks are effective only upon the availability of a priori information. A necessary flexibility in automatic recognition of anomalous events can be provided by effective account for an expertise of experts analyzing the data manually. Modeling of the logics of the expert-interpreter can be achieved by application of mathematical methods on the basis of fuzzy logics, which have been developed recently. The methods to be used are based on the theory of discrete mathematical analysis (DMA). DMA has demonstrated considerable achievements in a number of geophysical and geodynamic applications, and started to be applied in geomagnetic studies: recognition of natural anomalies and estimation of their intensity using a unified scale in geoelectric and geomagnetic gravity records [Agayan et al., 2016; Gvishiani et al., 2014, 2016; Soloviev et al., 2013, 2016]. Algorithmic DMA approach enabled one to recognize low-amplitude geomagnetic pulsations of different types and their time limits [Zelinskiy et al., 2014]. What is important in our studies is that DMA-based methods have been implemented for an automated and unified anthropogenic anomaly recognition, such as spikes and jumps, in magnetograms from ground and satellite magnetometers [Bogoutdinov et al., 2010; Sidorov et al., 2012; Soloviev et al., 2009, 2012a, 2012b]. These methods are applicable to both 1-minute and 1-second recordings, and are capable to operate continuously providing large data streams processing with high degree of reliability.
The wider introduction of advanced technologies, the more sensitive become their failures due to the impact of space weather. One of the most significant factors of space weather for terrestrial technological systems are electric geomagnetically induced currents (GIC) in the surface layers of the Earth caused by abrupt changes of the geomagnetic field. GIC are dangerous for pipelines, high-voltage power lines, railway equipment, communications cables, telephone and telegraph lines. The most intense currents (up to hundreds of amperes) and fields (more 10 V/m) are excited at auroral latitudes during magnetic storms and substorms [Lanzerotti, 2001]. Induced currents cause saturation, overheating and even damage of the high-voltage transformers in power systems. Under the influence of GIC cathodic protection of pipelines, supporting pipe negative potential relative to the ground, distorted, which dramatically increases the rate of corrosion during geomagnetic storms and reduces the lifetime of a pipeline. Operational forecast of possible critical levels of GIC can be used by operators to reduce the risk of catastrophic consequences.
 |
| Figure 6 |
The estimation of the space weather parameters critical for ground technological systems requires the construction of statistical maps of magnetic field variability ($dB/dt$). Statistical maps can be used as input parameters for the calculation of GIC in a particular technological system. Presumably, the intensity of the expected GICs can be very inhomogeneous in space and does not coincide with the region of maximum magnetic disturbances. The possible methodology in the GIC model should involve the calculation of the amplitude of total magnetic field derivative and 2D interpolation across the Earth's surface. As an example, the maps with geomagnetic variations and geomagnetic variability during magnetic storm on March 17, 2015 are shown in Figure 6. This figure enables one to compare the substorm intensity, as measured by $\Delta X$ magnitude of the magnetic bay, and amplitude of magnetic field variability, measured by derivative $|dX/dt|$. The comparison shows that there is no one-to-one correspondence between the substorm intensity and the level of geomagnetic variability. Maximal intensity is observed in a narrow latitudinally localized region from Scandinavia to eastern Siberia. Substorm develops in the morning sector, at $\Phi \sim 59$°, whereas maximal variability is observed in the early morning sector also, but at $\Phi \sim 65$°.
Thus, the existing database of ULF wave power should be augmented with the world-wide hourly maps with:
An hourly ULF wave power index, analogous to geomagnetic indices, has been derived from ground and satellite magnetometer data. A wide range of space physics studies, such as substorm physics, relativistic electron energization, SW-ionosphere coupling, etc., may benefit from the introduction of this index. The database for the interval 1991 up to nowadays is freely available via ulf.gcras.ru website for testing and validation. Comments and requests for specific intervals or parameters of the ULF index construction are highly welcomed. A long-term time series of wave indices, characterizing the level of IMF and geomagnetic field turbulence, would be a useful database for the development and statistical verification of this high-Reynolds-number phenomenology of the magnetosphere. Using the ULF index of the IMF variability it was proved that when the IMF is more turbulent, the effective degree of its coupling to magnetosphere is higher. The enhanced ULF wave power in the SW was shown to substantially enhance the convection strength in both the dayside and nightside high latitude ionosphere. The variability of SW and magnetospheric conditions might be an important factor in triggering magnetospheric substorms.
During storms, magnetospheric satellites suffer numerous anomalies from "killer" electrons. Relativistic electron flux has a time delay $\sim 1-2$ days with respect to the ULF-index. Thus, this index could be used as a "precursor" of the risk of magnetospheric satellite anomalies. An ease of use of a single parameter characterizing ULF wave activity in various domains of the outer space greatly facilitates the elaboration of statistical models for nowcasting and predicting relativistic electron fluxes.
The provisional ULF index has some drawbacks and deficiencies, but an ongoing research will overcome them and provide a more effective and robust index.
Agayan, S., S. Bogoutdinov, A. Soloviev, R. Sidorov (2016), The study of time series using the DMA methods and geophysical applications, Data Science Journal, 15, no. 16, p. 1–21.
Baker, D. N., T. Pulkkinen, X. Li, S. G. Kanekal, J. B. Blake, R. S. Selesnick, G. D. Reeves, H. E. Spence, G. Rostoker (1998), Coronal mass ejections, magnetic clouds, and relativistic magnetospheric electron events: ISTP, J. Geophys. Res., 103, p. 17279–17291, doi:10.1029/97JA03329.
Bogoutdinov, Sh. R., et al. (2010), Recognition of disturbances with specified morphology in time series. Part 1: Spikes on magnetograms of the worldwide INTERMAGNET network, Physics of the Solid Earth, 46, p. 1004–1016, doi:10.1134/S1069351310110091.
Borovsky, J. E., H. O. Funsten (2003), The MHD turbulence in the Earth's plasma sheet: dynamics, dissipation, and driving, J. Geophys. Res., 108, p. 1284, doi:10.1029/2002JA009625.
Borovsky, J. E., M. H. Denton (2014), Exploring the cross correlations and autocorrelations of the ULF indices and incorporating the ULF indices into the systems science of the solar wind-driven magnetosphere, J. Geophys. Res., 119, p. 4307–4334, doi:10.1002/2014JA019876.
Borovsky, J. E., R. C. Elphic, H. O. Funsten, M. F. Thomsen (1997), The Earth's plasma sheet as a laboratory for flow turbulence in high-$\beta$ MHD, J. Plasma Phys., 57, p. 1–34, doi:10.1017/S0022377896005259.
Currie, J. L., C. L. Waters (2014), On the use of geomagnetic indices and ULF waves for earthquake precursor signatures, J. Geophys. Res., 119, p. 992–1003, doi:10.1002/2013JA019530.
Elkington, S. R., M. K. Hudson, A. A. Chan (1999), Acceleration of relativistic electrons via drift-resonant interaction with toroidal-mode Pc5 ULF oscillations, Geophys. Res. Lett., 26, p. 3273–3276, doi:10.1029/1999GL003659.
Goertz, C. K., R. A. Smith (1989), The thermal catastrophe model of substorms, J. Geophys. Res., 94, p. 6581–6596, doi:10.1029/JA094iA06p06581.
Gvishiani, A., R. Lukianova, A. Soloviev, A. Khokhlov (2014), Survey of geomagnetic observations made in the northern sector of Russia and new methods for analyzing them, Surveys in Geophysics, 35, p. 1123–1154, doi:10.1007/s10712-014-9297-8.
Gvishiani, A., A. Soloviev, R. Krasnoperov, R. Lukianova (2016), Automated hardware and software system for monitoring the Earth's magnetic environment, Data Science Journal, 15, p. 18, doi:10.5334/dsj-2016-018.
Hattori, K. (2004), ULF geomagnetic changes associated with large earthquakes, Terr. Atmos. Ocean Sci., 15, p. 329–360, doi:10.3319/TAO.2004.15.3.329(EP).
Heilig, B., S. Lotz, J. Vero, P. Sutcliffe, J. Reda, K. Pajunpaa, T. Raita (2010), Empirically modeled Pc3 activity based on solar wind parameters, Ann. Geophys., 28, p. 1703–1722, doi:10.5194/angeo-28-1703-2010.
Hudson, M. K., S. R. Elkington, J. G. Lyon, C. C. Goodrich (2000), Increase in relativistic electron flux in the inner magnetosphere: ULF wave mode structure, Adv. Space Res., 25, p. 2327–2337, doi:10.1016/S0273-1177(99)00518-9.
Kamide, Y. (2001), Interplanetary and magnetospheric electric fields during geomagnetic storms: What is more important, steady-state fields or fluctuating fields?, J. Atmosph. Solar-Terrestrial Phys., 63, p. 413–420, doi:10.1016/S1364-6826(00)00176-0.
Kim, H.-J., L. R. Lyons, S. Zou, A. Boudouridis, D.-Y. Lee, C. Heinselman, M. McCready (2009), Evidence that solar wind fluctuations substantially affect the strength of dayside ionospheric convection, J. Geophys. Res., 114, p. A11305, doi:10.1029/2009JA014280.
Kim, H. J., L. Lyons, A. Boudouridis, V. Pilipenko, A. J. Ridley, J. M. Weygand (2011), Statistical study of the effect of ULF fluctuations in the IMF on the cross polar cap potential drop for northward IMF, J. Geophys. Res., 116, p. A10311, doi:10.1029/2011ja016931.
Kozyreva, O. V., N. G. Kleimenova (2008), Estimate of the dayside geomagnetic wave activity during magnetic storms with the use of new ULF index, Geomag. Aeron., 48, p. 511–519.
Kozyreva, O. V., N. G. Kleimenova (2009), Variations of ULF-index of geomagnetic pulsations during strong magnetic storms, Geomag. Aeron., 49, p. 446–459, doi:10.1134/s0016793209040021.
Kozyreva, O. V., N. G. Kleimenova (2010), Variations of the ULF-index of dayside geomagnetic pulsations during recurrent magnetic storms, Geomag. Aeron., 50, p. 799–809.
Kozyreva, O., V. Pilipenko, M. J. Engebretson, K. Yumoto, J. Watermann, N. Romanova (2007), In search of a new ULF wave index: Comparison of Pc5 power with dynamics of geostationary relativistic electrons, Planetary Space Science, 55, p. 755–769, doi:10.1016/j.pss.2006.03.013.
Lanzerotti, L. J. (2001), Space weather effects on technologies, Space Weather (Song et al., eds.), p. 11–22, AGU, Washington, D.C, doi:10.1029/gm125p0011.
Li, X., M. Temerin, D. N. Baker, G. D. Reeves, D. Larson (2001), Quantitative prediction of radiation belt electrons at geosynchronous orbit based solar wind measurements, Geophys. Res. Lett., 28, p. 1887–1890, doi:10.1029/2000GL012681.
Liu, W. W., G. Rostoker, D. N. Baker (1999), Internal acceleration of relativistic electrons by large-amplitude ULF pulsations, J. Geophys. Res., 104, p. 17391–17407, doi:10.1029/1999JA900168.
Lyons, L. R., et al. (2009), Evidence that solar wind fluctuations substantially affect global convection and substorm occurrence, J. Geophys. Res., 114, p. A11306, doi:doi:10.1029/2009JA014281.
Mann, I. R., T. P. O'Brien, D. K. Milling (2004), Correlations between ULF wave power, solar wind speed, and relativistic electron flux in the magnetosphere: Solar cycle dependence, J. Atmosph. Solar-Terr. Physics, 66, p. 187–198, doi:10.1016/j.jastp.2003.10.002.
Mathie, R. A., I. R. Mann (2001), On the solar wind control of Pc5 ULF pulsation power at mid-latitudes: Implications for MeV electron acceleration in the outer radiation belt, J. Geophys. Res., 106, p. 29783–29796, doi:10.1029/2001ja000002.
McPherron, R. L. (1997), The role of substorms in the generation of magnetic storms, Magnetic Storms (Tsurutani et al., eds.), p. 280, AGU, Washington D.C, doi:10.1029/GM098p0131.
Molchanov, O. A., M. Hayakawa (2008), Seismo Electromagnetics and Related Phenomena: History and Latest Results, 189 pp., TERRAPUB, Tokyo.
O'Brien, T. P., R. L. McPherron, D. Sornette, G. D. Reeves, R. Friedel, H. J. Singer (2001), Which magnetic storms produce relativistic electrons at geosynchronous orbit?, J. Geophys. Res., 106, p. 15533–15544, doi:10.1029/2001JA000052.
Pilipenko, V. A. (1990), ULF waves on the ground and in space, J. Atmospheric Terrestrial Physics, 52, p. 1193–1209, doi:10.1016/0021-9169(90)90087-4.
Pilipenko, V., O. Kozyreva, M. Engebretson, W. J. Hughes, S. Solovyev, K. Yumoto (1998), Coupling between substorms and ULF disturbances in the dayside cusp, Proc. of the International Conference "Substorms-4", p. 573–576, Kluwer Academic Publishers, Boston.
Pilipenko, V., N. Romanova, L. Simms (2008), ULF wave power index for space weather applications, COST-724 Final Report "Developing the scientific basis for monitoring, modeling and predicting space weather", p. 279–288, ESA, Brussels.
Pilipenko, V., N. Yagova, N. Romanova, J. Allen (2006), Statistical relationships between the satellite anomalies at geostationary orbits and high-energy particles, Advances in Space Research, 37, p. 1192–1205, doi:10.1016/j.asr.2005.03.152.
Pokhotelov, O. A., V. A. Pilipenko, M. Parrot (1999), Strong atmospheric disturbances as a possible origin of inner zone particle diffusion, Annales Geophysicae, 17, p. 526–532, doi:10.1007/s00585-999-0526-2.
Posch, J. L., M. J. Engebretson, V. A. Pilipenko, W. J. Hughes, C. T. Russell, L. J. Lanzerotti (2003), Characterizing the long-period ULF response to magnetic storms, J. Geophys. Res., 108, p. 1029, doi:10.1029/2002JA009386.
Potapov, A. S., B. Tsegmed, L. V. Ryzhakova (2014), Solar cycle variation of "killer" electrons at geosynchronous orbit and electron flux correlation with the solar wind parameters and ULF waves intensity, Acta Astronautica, 93, p. 55–63, doi:10.1016/j.actaastro.2013.07.004.
Reeves, G. D. (1998), Relativistic electrons and magnetic storms: 1992–1995, Geophys. Res. Lett., 25, p. 1817–1820, doi:10.1029/98GL01398.
Romanova, N., V. Pilipenko (2008), ULF wave indices to characterize the solar wind – magnetosphere interaction and relativistic electron dynamics, Acta Geophysica, 57, p. 158–170.
Romanova, N., V. Pilipenko, N. Crosby, O. Khabarova (2007), ULF wave index and its possible applications in space physics, Bulgarian Journal of Physics, 34, p. 136–148.
Rostoker, G., S. Skopke, D. N. Baker (1998), Relativistic electrons in the magnetosphere, Geophys. Res. Lett., 25, p. 3701–3704, doi:10.1029/98GL02801.
Samson, J. C., D. D. Wallis, T. J. Hughes, F. Creutzberg, J. M. Ruohoniemi, R. A. Greenwald (1992), Substorm intensifications and field line resonances in the nightside magnetosphere, J. Geophys. Res., 97, p. 8495–8518, doi:10.1029/91JA03156.
Shprits, Y. Y., et al. (2008a), Review of modeling of losses and sources of relativistic electrons in the outer radiation belt I: Radial transport, J. Atmospheric and Solar-Terrestrial Physics, 70, p. 1679–1693, doi:10.1016/j.jastp.2008.06.008.
Shprits, Y. Y., D. A. Subbotin, N. P. Meredith, S. Elkington (2008b), Review of modeling of losses and sources of relativistic electrons in the outer radiation belt II: Local acceleration and loss, J. Atmospheric and Solar-Terrestrial Physics, 70, p. 1694–1713, doi:10.1016/j.jastp.2008.06.014.
Sidorov, R. V., A. A. Soloviev, Sh. R. Bogoutdinov (2012), Application of the SP algorithm to the INTERMAGNET magnetograms of the disturbed geomagnetic field, Physics of the Solid Earth, 48, p. 410–414, doi:10.1134/S1069351312040088.
Simms, L. E., V. A. Pilipenko, M. J. Engebretson (2010), Determining the key drivers of long-period magnetospheric ULF waves, J. Geophys. Res., 115, p. A10241, doi:10.1029/2009JA015025.
Simms, L. E., V. A. Pilipenko, M. J. Engebretson, G. D. Reeves, A. J. Smith, M. Clilverd (2014), Prediction of relativistic electron flux at geostationary orbit following storms: Multiple regression analysis, J. Geophys. Res., 119, p. 7297–7318, doi:10.1002/2014ja019955.
Simms, L. E., M. J. Engebretson, A. J. Smith, M. Clilverd, V. Pilipenko, G. D. Reeves (2015), Analysis of the effectiveness of ground-based VLF wave observations for predicting or nowcasting relativistic electron flux at geostationary orbit, J. Geophys. Res., 120, p. 2052–2060, doi:10.1002/2014JA020337.
Simms, L. E., M. J. Engebretson, V. A. Pilipenko, G. D. Reeves, M. A. Clilverd (2016), Empirical predictive models of daily relativistic electron flux at geostationary orbit: Multiple regression analysis, J. Geophys. Res., 121, p. 3181–3197, doi:10.1002/2016JA022414.
Soloviev, A. A., et al. (2009), Detection of hardware failures at INTERMAGNET observatories: application of artificial intelligence techniques to geomagnetic records study, Russ. J. Earth Sci., 11, p. ES2006, doi:10.2205/2009ES000387.
Soloviev, A. A., et al. (2012a), Recognition of disturbances with specified morphology in time series: Part 2. Spikes on 1-s magnetograms, Physics of the Solid Earth, 48, p. 395–409, doi:10.1134/S106935131204009X.
Soloviev, A., et al. (2012b), Automated recognition of spikes in 1 Hz data recorded at the Easter Island magnetic observatory, Earth Planets Space, 64, p. 743–752, doi:10.5047/eps.2012.03.004.
Soloviev, A., S. Bogoutdinov, A. Gvishiani, R. Kulchinskiy, J. Zlotnicki (2013), Mathematical tools for geomagnetic data monitoring and the INTERMAGNET Russian segment, Data Science Journal, 12, p. 114–119, doi:10.2481/dsj.WDS-019.
Soloviev, A., S. Agayan, S. Bogoutdinov (2016), Estimation of geomagnetic activity using measure of anomalousness, Annals of Geophysics, 59, p. G0653, doi:10.4401/ag-7116.
Surkov, V., V. Pilipenko (1999), The physics of pre-seismic electromagnetic ULF signals, Atmospheric and Ionospheric Electromagnetic Phenomena Associated with Earthquakes, edited by M. Hayakawa, p. 357–370, TERRAPUB, Tokyo.
Tverskoy, B. A. (1968), Dynamics of the Radiation Belts of the Earth, 194 pp., Nauka, Moscow.
Yagova, N. V., V. A. Pilipenko, A. S. Rodger, V. O. Papitashvili, J. F. Watermann (2000), Long period ULF activity at the polar cap preceding substorm, Proc. 5th International Conference on Substorms, St. Petersburg, p. 603–606, ESA Publications Division, Noordwijk, the Netherlands.
Zelinskiy, N. R., et al. (2014), Algorithm for recognizing Pc3 geomagnetic pulsations in 1-s data from INTERMAGNET equatorial observatories, Physics of the Solid Earth, 50, p. 240–248, doi:10.1134/S106935131402013X.
Received 19 January 2017; accepted 22 January 2017; published 15 February 2017.


Citation: Pilipenko V. A., O. V. Kozyreva, M. J. Engebretson, A. A. Soloviev (2017), ULF wave power index for space weather and geophysical applications: A review, Russ. J. Earth Sci., 17, ES2002, doi:10.2205/2017ES000597.
Copyright 2017 by the Geophysical Center RAS.