RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 16, ES3005, doi:10.2205/2016ES000569, 2016
V. P. Trubitsyn1,2, M. N. Evseev1
1Institute of Physics of the Earth, Russian Academy of Sciences, Moscow, Russia
2Institute of Earthquake Prediction Theory and Mathematical Geophysics, Russian Academy of Sciences, Moscow, Russia
A mantle plume is a rising stream of vigorous thermal convection, which takes a mushroom-like shape and has a finite lifetime. When the plume approaches to the lithosphere the plume head first penetrates it. During the solidification of magma near the plume head a large igneous province (LIP) is formed. Later the plume tail penetrates the moving plate and forms a chain of volcanoes oriented in the direction of plate motion. A hot spot (HS) is the end location of the chain or the place of modern penetration of the plume tail in the form of an active volcano. In existing numerical models of mantle convection the plume tails are continuous streams. The question of why between the volcanic islands there is an interval of several hundred km (which corresponds to the interval between eruptions of several million years) is discussed starting from the time of emergence of the concept of plumes. This work on the numerical models shows that a primary plume originates only at the mantle bottom and dies not by attenuation but by pairwise association of two adjacent plumes. Also the work studies the internal structure of mantle plumes. It is shown that the plume tail is a pulsating jet already in the lower mantle with periods of several million years. When the plume encounters the 660 km phase boundary it flattens out against this surface and transforms into secondary more frequent plumes in the form of the individual thermals (heads detached from tails).
Volcanoes on the Earth are divided into two types. The volcanic sources of subduction zones and rifts originate at the plate boundaries in the upper mantle and are moved horizontally with plates and continents. The volcanoes manifested in the form of hotspots and large igneous provinces are caused by mantle plumes that originate at the bottom of the mantle, regardless of any boundaries of lithospheric plates.
A mantle plume is a rising jet of high-intensity thermal convection with mushroom shape which is preserved up to several hundred million years. When a head of a mantle plume breaks through the lithosphere and the crust, a Large Igneous Province (LIP) arises in the form of basaltic traps on continents and oceanic plateaus at the bottom of the oceans. After the material of the plume tail penetrates the moving oceanic plate, a chain of volcanic islands is created which ends with a modern active volcano called a hot spot (HS). Such chains are well observed at the bottom of oceans. The examples of typical volcanic chains are the Hawaiian-Emperor volcanic islands in the Pacific Ocean and the Reunion hot spot in the Indian Ocean. On the continents volcanic chains are almost not visible because the plume tail is difficult to break through the thick continental lithosphere and crust.
 |
| Figure 1 |
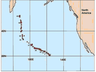
Figure 1 shows the entire Hawaiian-Emperor chain of volcanic islands in the Pacific Ocean. These islands were formed when the plume tail, which probably arose in the mantle more than a hundred million years ago, intruded into the moving oceanic plate. The Large Igneous Province created by the plume head apparently already sunk into the subduction zone of the Pacific Plate. This chain of volcanic islands has a bend separating it into two parts represented by the Emperor Seamounts and the Hawaiian Islands. This bend of the chain is currently explained by the change in motion of the Pacific Plate of from North to Northwest about 43 million years ago.
The interpretation of the Hawaiian-Emperor chain of volcanic islands was one of the fundamental arguments in justifying the theory of plate tectonics and mantle plumes.
Wilson [1963] suggested that the Hawaiian and other volcanic island chains may have formed due to the movement of a plate over a stationary "hotspot" in the mantle. In 1968 Christofferson suggested that the bend of the island chains was associated with changes in the direction of motion of the Pacific Plate [Hsu, 1982]. Morgan suggested and proved that the source of heat and magma for the volcanic Hawaiian Islands was a plume rising from the deep mantle [Morgan, 1971, 1972].
 |
| Figure 2 |
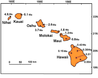
Figure 2 shows more details about the chain of volcanic islands in the vicinity of the Hawaiian hotspot with data about their ages.
As one can see from Figure 1 and Figure 2, the distance between the volcanic islands is several hundred km. Figure 2 shows that the islands Nihai and Kauai were formed about 5 Myr ago and shifted relative to the plume, which is now under Island of Hawaii, approximately by 500 km. This conforms to the North-West motion of the Pacific Plate. The comparison with the ages of the islands by radioisotope data shows that Pacific Plate was moving at an average speed of 10 cm/yr. The plume penetrated the lithosphere and crust not continuously but by in batches (quanta) and created volcanoes at intervals of several million years. There was no single interval between the eruptions of magma but a set of intervals.
Mjelde and Faleide [2009] have demonstrated that both in the Hawaiian and Icelandic volcanism there exists a characteristic interval of 15 million years. It has been argued that this interval is not connected with the phenomena on the 660 km phase boundary, but is due to processes at the place of origin of plumes at the core-mantle boundary.
Mjelde et al. [2010] analyzed the global volcanism on the Earth in the Cenozoic, including the hot spots of the Pacific, Atlantic, and Indian Ocean, the Yellowstone and the volcanism of Europe. There were detected the primary peaks of activity 10, 22, 30, 40, 49, and 60 Myr and the secondary peaks 4, 15, 34, 45 and 65 Myr. Spectral analysis revealed a dominant period of 10 Myr and a secondary period of 5 Myr.
O'Connor et al. [2002] studied the distribution of intraplate volcanism by the method of $^{40}$Ar/$^{39}$Ar ages. They found that the chain of Foundation seamounts was generated due to pulsation of a hot mantle jet with periods of the order of 1 Myr.
Properties of thermal plumes have been intensively studied in numerical models and laboratory experiments for more than two decades, see for examples [Campbell, 2005;
Farnetani and Hofmann, 2009; Schubert et al., 2004; Tosi and Yuen, 2013]. The numerical models demonstrate that plumes arise spontaneously at the bottom of the mantle under high-intensity thermal convection. The plumes can shift horizontally at the 600 km phase boundary and then become thinner in the less viscous upper mantle, see for example [Tosi and Yuen, 2011; Trubitsyn and Evseev, 2014]. The analytical instability study of a rising plume indicates the possibility of solitary waves propagating in the plume [Olson, 1990; Schubert et al., 2004]. According to [Farnetani and Hofmann, 2009, 2010] chemically and isotopically heterogeneous of plumes change their form in lower mantle. For example, initial lenses of size $100 \times 10$ km in the TBL are stretched into filaments 500–1000 km long.
However, the currently available numerical models of mantle plumes show only continuous jets and did not reveal any wave instability in plumes. Therefore, till now the unsolved problem remains why the plume tails generate discrete magma eruptions.
The present paper shows the results of numerical modeling of the evolution of mantle plumes with variable mantle viscosity, phase transitions and spherical effects. It is shown that the plume tail is a pulsating jet already in the lower mantle and the main period of pulsation is equal to about 10 million years. When the plume encounters the 660 km phase boundary, it flattens out against this surface and transforms into secondary more frequent plumes in the form of individual thermals (heads detached from tails).
The governing equations of mass, momentum, and energy conservation in the heated compressible viscous mantle in an extended Boussinesq approximation (EBA) have the form [Schubert et al., 2004]
\begin{equation} \tag*{(1)} - \frac{\partial p}{\partial x_i} + \frac{\partial \tau_{ij}}{\partial x_j} + \left( RaT - \sum\limits_k R b_k \Gamma_k \right) \delta_{i3} =0 \end{equation} \begin{eqnarray*} \frac{\partial T}{\partial t} + U_i \frac{\partial T}{\partial x_i} + Di(T+ T_s) U_z = \end{eqnarray*} \begin{equation} \tag*{(2)} \frac{\partial}{\partial x_i} \left( k \frac{\partial T}{\partial x_i} \right) + \frac{Di}{Ra}\tau_{ij} \frac{\partial U_i}{\partial x_j} + \rho_0 H \end{equation} \begin{equation} \tag*{(3)} \frac{\partial U_j}{\partial x_j} =0 \end{equation} \begin{equation} \tag*{(4)} \tau_{ij} = \eta \left( \frac{\partial U_i}{\partial x_j} + \frac{\partial U_j}{\partial x_i} \right) \end{equation}where $\tau_{ij}$ is the deviator of the tensor of viscous stresses, $ U_i$ is the velocity vector; $p$ is dynamic pressure; $T$ is temperature; $T_s$ is surface temperature; $H$ is internal heating; $Ra = \alpha \rho_0 g \Delta TD^3/(\kappa_0 \eta_0$) is the thermal Rayleigh number; $Rb_k= \delta \rho_k D^3 g/(\kappa_0 \eta_0$) are the phase-change Rayleigh numbers; $\delta \rho_l$ is the density jump across a phase change; $Di = Dg\alpha_0/c_p$ is dissipation number; $D$ is the mantle thickness; $\Delta T$ is the temperature difference across the whole mantle; $\rho_0$, $\eta_0$, $c_p$, $\alpha_0$, $k_0$, $\kappa_0 = k_0/(\rho_0c_p$) are the mean values of density, viscosity, heat capacity, thermal expansivity, thermal conductivity, and thermal diffusivity, respectively. $\Gamma_l$ is the phase function
\begin{eqnarray*} \Gamma_l = \frac{1}{2} \left( 1+ th \frac{z-z_l(T)}{w_l} \right) \end{eqnarray*}where $z_l$ is the depth of a phase change, and $w_l$ is the width of a phase transition. The dependence of depth of a phase change on temperature is defined as
\begin{eqnarray*} z_l(T) = z_l^0 + \gamma_l (T-T_l^0) \end{eqnarray*}where $\gamma_l$ is the Clapeyron slope, $z_l^0$ and $T_l^0$ are the average depth and temperature of a phase change. Small thermal effects of phase transitions in the heat transfer equation (2) are ignored.
The approximation EBA takes into account the thermal effects of compressible fluid in the equation of the temperature balance (3), i.e., adiabatic heating or cooling of descending and ascending flows, respectively. However, for simplicity it neglects smaller effects of compressibility in equation (1) for mass transfer (which becomes the incompressibility equation) and the Stokes equation (2) [Trubitsyn and Trubitsyn, 2015]. In the EBA approach the temperature is measured from a constant real temperature at the upper surface layer $T_s \sim 300$ K, so the full absolute temperature of the mantle is equal to $T + T_s$.
The equations (1)–(4) typically use simple boundary conditions with impermeable, shear stress free, and isothermal boundaries. The temperatures on the upper and lower boundary are taken equal to $T_s = 300$ K and $T = T_s + \Delta T$, respectively. The initial conditions correspond to a conductive heating of the layer with an arbitrary small perturbation of temperature.
For the nondimensionalization we use the following scaling factors: the mantle thickness $D$ for distance; the temperature difference across the whole mantle $\Delta T$ for temperature; the characteristic values of mean density $\rho_0$, viscosity $\eta_0$ and heat capacity $c_p$; the characteristic values of thermal expansivity $\alpha_0$ and thermal conductivity $k_0$; as well as the values $\kappa = k_0/(\rho_0c_p$) for thermal diffusivity, $t_0 = D^2/\kappa$ for time, $U_0 = \kappa/D$ for velocity, $q_0 = k_0 \Delta T/D$ for heat flux, $\sigma_0 = \eta_0 \kappa/D^2$ for dynamic pressure and stress, $p_0= \rho_0 gD$ for static pressure, and $H_0 = c_p \kappa \Delta T/D^2$ for the internal heat generation.
The parameter values for the mantle were taken from [Schubert et al., 2004; Tosi and Yuen, 2011] and are the following: $D = 2890$ km, $\rho_0 = 4.5 \times 10^3$ kg m$^{-3}$, $c_p = 1.25 \times 10^3$ J kg$^{-1}$ K$^{-1}$, $\eta_0 = 5 \times 10^{21}$ Pa s, $\kappa_0 = 0.59 \times 10^{-6}$ m$^2$ s$^{-1}$, $\alpha_0 = 2.0 \times 10^{-5}$ K$^{-1}$, $\Delta T = 3500$ K, $H = 5.2 \times 10^{-13}$ W kg$^{-1}$. The main phase transitions in the mantle occur at depths 420 km, 660 km and 2890 km. Their density jumps equal to 6.7%, 7.6% and 1.5% and Clapeyron slopes equal to 3 MPa/K, $-2.5$ MPa/K and 13 MPa/K, respectively.
With these parameter values the Rayleigh number for compressible mantle, dissipation number and the dimensionless density of heat sources are equal to $Ra = 1.5 \times 10^7$, $Di = 0.45$, $H = 14$, respectively. The scaling factors for velocities and time are equal to $3.1 \times 10^{-3}$ cm/yr and $2.6 \times 10^{11}$ yr. The dimensionless parameters of mantle viscosity, coefficient of thermal expansion and thermal diffusivity can be functions of depth and temperature.
The study of mantle plumes was conducted in the model of thermal convection in the spherical annulus domain near the equator bounded by constant latitude $89\mbox{°} <\varphi <91\mbox{°}$, which is similar to that of [Hernlund and Tackley, 2008; Ismail-Zadeh and Tackley, 2010]. This model, in contrast to commonly used models of a cylindrical ring, axisymmetric sphere and Cartesian layer, accurately accounts for the spherical geometric effects.
 |
| Figure 3 |
The dimensional coefficients of thermal expansion $\alpha$, thermal conductivity $k$, and thermal diffusivity $\kappa$ as functions of the dimensionless depth $x = 1 - z$ given in [Matyska and Yuen, 2005; Tosi and Yuen, 2011; Tosi et al., 2013] were approximated as (see Figure 3)
\begin{eqnarray*} \alpha = 42 \times 10^{-5} (2.3 + x)^{-3} \; \mathrm{K}^{-1} \end{eqnarray*} \begin{eqnarray*} k = 3(1 +3.3x) \; \mathrm{W/mK} \end{eqnarray*} \begin{equation} \tag*{(5)} \kappa= \frac{k}{\rho c_{p}} = 1.8(1+3.3x) 10^{-6} \; \mathrm{m}^2 \; \mathrm{s}^{-1} \end{equation}Accordingly, the dimensionless coefficients of thermal expansion and thermal diffusivity (for the selected scaling factors $\alpha_0 = 2\times 10^{-5}$ K$^{-1}$ and $\kappa_0=10^{-6}$ m$^2$/s) will be equal $\alpha = 21(2.3 + x)^{-3}$ and $\kappa = 1.8(1+3.3 x)$.
The dimensionless viscosity as a function of dimensionless temperature $T$ and pressure $p$ was taken according to [Trubitsyn, 2016]. This function agrees with the data of laboratory measurements at low pressures and the data on post-glacial rebound in the whole mantle:
\begin{equation} \tag*{(6)} \eta (p, T) = A \exp \left(\frac{E_0 + pV_0}{T + Ts} \right) \end{equation}where $E_0$ is the activation energy, and $V_0$ is the activation volume.
The value of the activation volume for the upper mantle was taken according to the laboratory measurement for olivine $V_0 = 4$ cm$^3$/mol, but for the lower mantle the smaller value was taken as $V_0 = 2$ cm$^3$/mol. The value of the activation energy for the whole mantle was taken according to the olivine data as $E_0 = 350$ kJ/mol.
 |
| Figure 4 |
The piecewise constant coefficient $A$ for the lower mantle was taken from the condition of normalization to the viscosity $\eta (p, T) = A = 5 \times 10^{21}$ Pa s at a depth of 700 km. The coefficient $A$ for the upper mantle was found from the condition of viscosity jump by a factor of 30 across the 660 km phase boundary (see Figure 4).
For numerical solving the convection equations (1)–(4) we use the finite element code Citcom [Tan et al., 2006; Zhong, 2000] which was complemented by the original graphics engine developed by M. Evseev [Trubitsyn and Evseev, 2014].
The solution of equations of convection (1)–(6) for the above specified models of compressible mantle with phase transitions and variables parameters shows that at $Ra>10^6$ nonstationary thermal convection occurs in the mantle with downward and upward flows in the form of the plumes. To ascertain the effects of the convection vigor and the jump in viscosity at the 660 km boundary on the evolution of mantle plumes we examined two models with no viscosity jump at $Ra=7.5 \times 10^6$ and with a jump of viscosity at $Ra=10^7$. The Appendix contains also a video for model of vigorous mantle convection at $Ra=8 \times 10^7$.
Figures 5–9 represent the calculated long-term evolution of mantle convection at $Ra=7.5 \times10^6$ with variably viscosity according to (6) without a viscosity jump at the phase boundary in the equatorial section of a sphere.
 |
| Figure 5 |
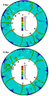
Figure 5 shows the equatorial section of the sphere for the time taken as the initial time point. Here one can see ten rising mantle jets. They have the form of plumes and are designated as $A$, $B$, $C$, $D$, $E$, $F$, $G$, $H$, $I$, $J$. The plume $A$ is only emerging at the bottom of the mantle. The rising plume $C$ has a characteristic mushroom shape, and its head reaches the lower third of the mantle. The heads of the rest plumes already have reached the surface and spread out along it. At time $t =12$ Myr the plume $A$ rises to a third of the mantle, and the lower part of the plume $D$ is horizontally shifted and jointed with plume $C$.
 |
| Figure 6 |
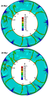
Figure 6 shows the structure of convection at a later time. At time $t = 24$ Myr the plume $A$ reached the 660 km phase boundary, and the plumes $C$ and $D$ joined into a single plume $C-D$. As a result, instead of ten plumes there are nine ones. Next, at time $t = 28$ Myr the base of the plume $A$ at the bottom of the mantle is approaching to the plume $B$. The head of the plume $A$ has reached the surface. Thus, from the generation of head plume A to its approach to the surface the time $t_{\mathrm{pl}} = 28$ Myr has passed, which corresponds to the average lifting speed of the head $V_{\mathrm{pl}} \approx$ 10 cm/yr. At time $t= 28$ Myr one can see that the plumes $A$ and $B$ begin to come together.
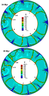 |
| Figure 7 |
Figure 7 represents the further evolution of convection. At time $t = 34$ Myr the base of the plume $A$ connected with the base of the plume $B$. These plumes also come close throughout the whole lower mantle. At time $t = 39$ Myr the plumes $C-D$ and $A-B$, that arose during the paired association of primary plumes, become ordinary plumes. Thus from this point on there are only eight plumes. The hydrodynamic mechanism of attraction of mantle plumes identified in the present work is apparently the cause of their death. Previously, the effect of interaction of convective jets was investigated in [Trubitsyn and Kharybin, 2012] and interpreted in the context of sedimentation convection which is an extension of the Rayleigh-Taylor and Stokes flows.
At times $t = 44$ Myr and $t = 50$ Myr there are eight tails of plumes. In the present models with low Rayleigh number $Ra=7.5 \times 10^6$ the thickness of plume tails range from 100 to 200 km. The width of heads can be 3–5 times more. Our numerical model reveals the new important result for inner structure of mantle plumes. The thickness of the plume tails is not constant in space and time.
Comparing the changes in the structure of plumes in time shows that plume tails are not continuous as is usually showed by numerical models. They are pulsing jets, i.e. they actually represent the heated channels through which the portions (quanta) of hotter material move from the bottom of the mantle. In the plume $A-B$ at $t = 44$ Myr the hot quantum is at the bottom of the mantle. At $t = 50$ Myr it arises at a distance of approximately one third the thickness of the mantle. Thus, velocity of this portion (quantum) of hot material equals $V_{\mathrm{qu}} \approx 15$ cm/yr. It follows that the time of uplift of individual quantum through the whole thickness of the mantle will be $t_{\mathrm{qu}} \approx 20$ Myr. So the velocity of quanta is nearly the same as of the plume head. Despite the fact that the head of the plume is larger, it rises in high viscous lower mantle. The smaller quantum rises inside low viscosity tail.
The quanta of material move inside the tail similar to a conveyor. There are about two quanta on the length of the tail at the same time. Therefore the interval between each eruption of magma from the tail must be equal to $t_{\mathrm{er}} \approx t_{\mathrm{qu}}/2 \approx 10$ Myr.
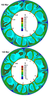 |
| Figure 9 |
Figure 9 shows that the structure of convection with eight mantle plumes continues to persist up to $t = 100$ Myr. However, at $t = 120$ Myr plumes $G$ and $H$ begin to draw together, and two new plumes $K$ and $L$ are generated at the bottom of the mantle. As a result, at this time point there are eight tails of plumes, one plume $K$ with a head and one emerging plume $L$. When comparing Figure 5 and Figure 9 we can see that the lifetime of most of mantle plumes exceeds 100 Myr. However there are some exceptions. Figure 5 and Figure 7 show that the plume $A$ lived only 34 Myr.
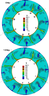 |
| Figure 10 |
Figure 10 presents the calculated long-term evolution of mantle convection at the equatorial section of a sphere at $Ra=10^7$ and a viscosity taken according to the formula (6) with a 30-fold jump on the boundary of upper and lower mantle.
In Figure 10 at the time conventionally taken as $t = 0$ one can see eight pulsating plume tails, which is similar to Figure 5 for the model with no jump in viscosity. The spatial distance between the quanta of hot material in the plume tails is approximately one third the thickness of the mantle.
The main difference of this model from previous ones is as follows. Without a viscosity jump when the plume enters the upper mantle it is only hindered and slowed down. Now with the viscosity jump due to lower viscosity of the upper mantle the plume accelerates, becomes thinner and can generate secondary fast plumes with large heads and very thin tails. These secondary plumes are not continuous in space and time. They do not born on the phase boundary, but are a continuation of the primary plume. Contrary to the primary plume these secondary plumes die due to exhaustion of each quantum and the primary plume is not able adequately supply them heat. Sometimes these secondary plumes have no tails and are similar to thermals.
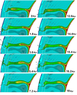 |
| Figure 11 |
Figure 11 shows a more detailed evolution of one plume that corresponds to the plume $B$ in Figure 10. At time $t = 0$ there are two quanta of hot material in the tail. The first quantum approaches the 660 km boundary. At $t = 1.8$ Myr the secondary mantle plume is born from this quantum. It has a thin tail and a large head. At $t = 3.6$ Myr the tail of this secondary plume breaks up, and his head spreads out along the surface. At the same time $t = 3.6$ Myr a new secondary plume is born at the phase boundary. At time $t = 5.4$ Myr this new secondary plume reaches the surface.
It is important that both new secondary plumes are originated from the same quantum of the primary tail. This shows that secondary plumes are born on the phase boundary approximately two times more often than quanta of hot material in the primary plume tail. As can be seen in video the secondary plumes are shifted horizontally compared to the location of the primary plume [Tosi and Yuen, 2011; Trubitsyn and Evseev, 2014].
The next quantum of material approaches the phase boundary at $t = 14.4$ Myr, and after that two secondary plumes are also born at $t = 14.4$ Myr and $t = 16.2$ Myr. The interval between portions of hot material in the plume is equal to $t = 14.4-1.8 = 12.6$ Myr.
Thus, in the convection model at $Ra=10^7$ each quantum of hot material in the plume tail rises from the bottom of the mantle to the surface during about 20 Myr. Since there is a conveyor with approximately two rising quanta, the interval between quanta is approximately 10 Myr.
Each quantum generates about two secondary plumes. However they are not born continuously. The first secondary plume appears just after the approach of the quantum to the phase boundary. The next secondary plume is occurs after $t = 2$ Myr. Then there is an interval $10 - 2 = 8$ Myr for coming of a next quantum through the primary plume tail. Therefore, two intervals $t = 2$ Myr and $t = 8$ Myr can be between the secondary plumes.
Thus, in the considered model the quantum of hot material comes to the phase boundary from the lower mantle every 10 Myr and then secondary plumes are born in upper mantle with intervals of $t = 2$ Myr and $t = 8$ Myr. Therefore there are at least two intervals for magma eruptions 2 Myr and 8 Myr.
The numerical simulations of thermal convection with variable viscosity and phase transitions show that mantle plumes represent the ascending mantle flows, often having the mushroom shape.
The authors created a high-resolution video of the calculated evolution of vigorous mantle convection for 200 Myr at $Ra=8 \times 10^7$ that can fit a little earlier Earth. In this case the quanta of hot material in the plume tail in the lower mantle are expressed even clearer, and their faster rise sometimes becomes similar to isolated thermals. In addition, the secondary plumes in the upper mantle occur more often. Therefore smaller periods should appear in the spectrum of eruptions.
 |
| Video |
The low-resolution video is produced from the original authors' video by the publisher to make its volume accessible for including into the PDF snd EPUB3 versions of the article. Original high-resolution video of mantle convection is freely accessible from RJES server (http://rjes.wdcb.ru/v16/2016ES000569/plumes-hr.html).
Campbell, I. H. (2005), Large igneous provinces and mantle plume hypothesis, Elements, 1, p. 265–269, doi:10.2113/gselements.1.5.265.
Farnetani, C. G., A. W. Hofmann (2009), Dynamics and internal structure of a lower mantle plume conduit, Earth and Planet. Sci. Lett., 282, p. 314–322, doi:10.1016/j.epsl.2009.03.035.
Farnetani, C. G., A. W. Hofmann (2010), Dynamics and internal structure of the Hawaiian plume, Earth and Planet. Sci. Lett., 295, p. 231–240, doi:10.1016/j.epsl.2010.04.005.
Hernlund, J. W., P. Tackley (2008), Modeling mantle convection in the spherical annulus, Physics of the Earth and Planet. Interiors, 171, p. 48–54, doi:10.1016/j.pepi.2008.07.037.
Hsu, K. J. (1982), Thirteen years of deep-sea drilling, Annual Review of Earth and Planet. Sci., 10, p. 109–128, doi:10.1146/annurev.ea.10.050182.000545.
Ismail-Zadeh, A., P. J. Tackley (2010), Computational Methods for Geodynamics, 313 pp., Cambridge Univ. Press, Cambridge, doi:10.1017/CBO9780511780820.
Matyska, C., D. A. Yuen (2005), The importance of radiative heat transfer on superplumes in the lower mantle with the new post-perovskite phase change, Earth and Planet. Sci. Lett., 234, p. 71–81, doi:10.1016/j.epsl.2004.10.040.
Mjelde, R., J. I. Faleide (2009), Variation of Icelandic and Hawaiian magmatism: evidence for co-pulsation of mantle plumes?, Mar. Geophys. Res., 30, p. 61–72, doi:10.1007/s11001-009-9066-0.
Mjelde, R., P. Wessel, R. D. Müller (2010), Global pulsations of intraplate magmatism through the Cenozoic, Lithosphere, 2, p. 361–378, doi:10.1130/L107.1.
Morgan, W. (1971), Convection plumes in the lower mantle, Nature, 230, p. 42–43, doi:10.1038/230042a0.
Morgan, W. J. (1972), Deep mantle convection plumes and plate motions, Am. Assoc. Petrol. Geol. Bull., 56, p. 203–213.
O'Connor, J. M., P. Stoffers, J. R. Wijbrans (2002), Pulsing of a focused mantle plume: Evidence from the distribution of Foundation Chain hotspot volcanism, Geophys. Res. Lett., 29, no. 9, p. 1350, doi:10.1029/2002GL014681.
Olson, P. (1990), Hot spots, swells and mantle plumes, Magma Transport and Storage, ed. M. P. Ryan, p. 33–51, JohnWiley & Sons Ltd., Chichester, U.K.
Paulson, A., Sh. Zhong, J. Wahr (2005), Modelling post-glacial rebound with lateral viscosity variations, Geophys. J. Int., 163, p. 357–371, doi:10.1111/j.1365-246X.2005.02645.x.
Schubert, G., D. L. Turcotte, P. Olson (2004), Mantle convection in the Earth and Planets, 940 pp., Cambridge Univ. Press, Cambridge, England, doi:10.1017/CBO9780511612879.
Tan, E., E. Choi, P. Thoutireddy, M. Gurnis, M. Aivazis (2006), GeoFramework: Coupling multiple models of mantle convection within a computational framework, Geochem. Geophys. Geosyst., 7, p. Q06001, doi:10.1029/2005GC001155.
Tarduno, J. A., et al. (2000), The Emperor Seamounts: Southward motion of the Hawaiian hotspot plume in Earth's mantle, Science, 301, p. 265–269.
Torsvik, T. H., K. Burke, B. Steinberger, S. Webb, L. Ashwal (2010), Diamonds sampled by plumes from the core-mantle boundary, Nature, 466, p. 352–355, doi:10.1038/nature09216.
Tosi, N., D. A. Yuen (2011), Bent-shaped plumes and horizontal channel flow beneath the 660 km discontinuity, Earth Planet. Sci. Lett., 312, p. 348–359, doi:10.1016/j.epsl.2011.10.015.
Tosi, N., D. Yuen, N. Renata, M. Wentzcovitch (2013), Mantle dynamics with pressure- and temperature-dependent thermal expansivity and conductivity, Physics of the Earth and Planet. Interiors, 217, p. 48–58, doi:10.1016/j.pepi.2013.02.004.
Trubitsyn, V. P. (2016), Viscosity distribution in the mantle convection models, Izvestiya, Physics of the Solid Earth, 52, no. 5, p. 627–636.
Trubitsyn, V. P., M. N. Evseev (2014), Mantle plumes at the boundary of upper and lower mantle, Dokl. Earth Sci., 459, Part 1, p. 1397–1399, doi:10.1134/S1028334X14110099.
Trubitsyn, V. P., E. V. Kharybin (2012), Extended Rayleigh-Taylor instability for suspension, sedimentation convection, Phys.-Chem. Kinetics in Gas Dynamics, 13, no. 2, p. 19 (http://chemphys.edu.ru/issues/2012-13-2/articles/314/).
Trubitsyn, V. P., A. P. Trubitsyn (2015), Effects of compressibility in the mantle convection equations, Izvestiya, Physics of the Solid Earth, 51, no. 6, p. 801–813, doi:10.1134/S1069351315060129.
Trubitsyn, V. P., M. N. Evseev, A. P. Trubitsyn (2015), Influence of continents and lithospheric plates on the shape of $D"$ layer and the spatial distribution of mantle plumes, Russ. J. Earth. Sci., 15, p. 3, doi:10.2205/2015ES000552.
Wilson, J. T. (1963), A possible origin of the Hawaiian Islands, Canadian J. of Phys., 41, p. 863–870, doi:10.1139/p63-094.
Zhong, S., M. T. Zuber, L. N. Moresi, M. Gurnis (2000), The role of temperature-dependent viscosity and surface plates in spherical shell models of mantle convection, J. Geophys. Res., B.105, p. 11,063–11,082, doi:10.1029/2000JB900003.
Received 22 August 2016; accepted 26 August 2016; published 10 September 2016.


Citation: Trubitsyn V. P., M. N. Evseev (2016), Pulsation of mantle plumes, Russ. J. Earth Sci., 16, ES3005, doi:10.2205/2016ES000569.
Copyright 2016 by the Geophysical Center RAS.