RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 16, ES2002, doi:10.2205/2016ES000566, 2016
A. F. Grachev
Institute of Physics of the Earth, Russian Academy of Sciences, Moscow, Russia
The paper presents data on relations between the petrofabrics of olivine crystals, elastic properties and thermal conductivity of mantle xenoliths in basalts from the Bohemian Massif, Pannonian Basin, Baikal Rift, and Lanzarote Island (Canary Islands). The sizes of the xenoliths themselves and olivine porphyroblasts and neoblasts in them were proved to be distributed according to the lognormal law. The identified seismic anisotropy of the xenoliths is controlled by the preferred orientation of the axis [100] of the olivine and partial melting zones in the xenoliths. The axes of the maximum shortening of the samples coincide with the dominant distribution mode of the axes [010] of olivine crystals. The major maxima of the axes [001] are parallel to the long axes of the xenoliths, whereas the maxima of [100] plot along the middle axis of the samples. The elastic properties $(V_p)$ and thermal conductivity ($\lambda$) of mantle xenoliths are controlled by parameters of the crystal lattice of olivine and the orientation of partial melting zones, which are correlated with the orientation of the long, middle, and short axes of the xenoliths. These data imply that the geometrically regular shapes of mantle xenoliths had been in situ formed in the mantle before these xenoliths were entrained by melts and brought to the surface.
The azimuthal seismic anisotropy of the oceanic lithosphere is actively studied by a wide circle of Earth scientists starting from the first paper, published by Hess, [1964]. The greatest progress in this field was achieved over the past decades by based on studying Phanerozoic ophiolite complexes with regard for experimental data on velocities of seismic waves and orientation of rock-forming minerals in oriented samples [Gass et al., 1984]. The significant lateral heterogeneities in Earth's deep-seated zones were lately identified using seismic tomography techniques in both the continental lithosphere and deeper sitting upper mantle.
The only source of information on the composition and state of rocks in the Earth's interiors is ultramafic xenoliths in alkali basalt lavas erupted in continental rifts and at oceanic islands. Because the xenolith-hosting lavas are young (their age ranges from 30 Ma to recent), the xenoliths themselves can provide unique information on the in statu nascendi composition and structure of the upper mantle. It has long been known that deep xenoliths show strongly anisotropic physical characteristics, including their elastic properties [Christensen, 1966; Verma, 1960]. Data on variations in the elastic properties with the shape and orientation of an ideal olivine crystal were extensively invoked to explain the azimuthal and seismic anisotropy of the lithosphere [Babushka et al., 1984]. Following [Nicolas et al., 1973], additional information for these studies was derived from the petrofabrics of ultramafic xenoliths, which make it possible to evaluate the strain that produces oriented fabrics in mantle xenoliths and the $P-T$ parameters at the depths from which the xenoliths were brought to the surface. The anisotropy of the lithosphere is commonly explained by the well-known fact that the elastic characteristics of olivine are different along its principal crystallographic axes. However, when discussing the anisotropy of large lithospheric blocks ranging from hundreds to a few thousand kilometers across, it is necessary to identify the mechanism that can control an ordered olivine distribution relative to the major elements of the surface structure.
This publication presents recently obtained information that demonstrates relations of certain characteristics of the petrofabrics, elastic properties, and thermal conduction of mantle xenoliths with their shapes, which in turn reflect the fragmentation of large blocks of the upper mantle.
Mantle xenoliths in basalt mostly have geometrically regular ellipsoidal shape and reach 60–80 cm along their major axes; although more rare xenoliths are irregularly shaped, angular, and smaller.
Extensive literature on mantle xenoliths provides however no information on their size distribution and no explanation why these xenoliths are mostly of geometrically regular shape. It is commonly thought that ascending basalt melt entrained their wall rocks [Kluegel, 1998, and several others], and the xenoliths acquired certain shapes when brought to the surface because of their interaction with the melt.
 |
| Figure 1 |
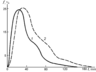
This hypothesis fails however to explain why the neck facies of fissure eruptions host practically no crustal xenoliths. Earlier we have addressed this problem when studying xenoliths in basalts from Tumbusun-Dulga volcano in the Khamar-Daban Range, southern central Siberia [Grachev et al., 1985]. We have measured the directions of the axes of 1800 ellipsoidal (in cross section) xenoliths. The size distribution of the xenoliths complies with the lognormal law (Figure 1).
According to Kolmogorov [1985], lognormal distributions are typical of products of crushing and shattering processes. It is however uncertain as to when these processes took place: whether when the xenoliths were entrained to the surface by melts or when their rocks resided in the upper mantle at depths of 40–70 km (spinel depth facies).
The former scenario seems to be unrealistic in view of the fact that, according to our data, melts usually carry no more than 20% xenoliths, which is insufficient for them to come in contact with one another and thus become eroded. Also, the times of melt ascent are too short: estimates for the ascent velocities of melts according to the Stokes law vary from 0.4 to 36 km/h [Morin and Corriveau, 1996; Spera, 1984].
The other scenario (in situ sorting) implies that separated fragments of the partly molten lherzolite mantle can interact during a long enough time spans when the mantle ascends from the asthenosphere level to the lithosphere where alkali basalt can be generated (40–70 km) [Grachev et al., 1985]. A decrease in the density of mantle material due to its melting allows individual fragments to revolve relative to one another under shear strain (see below for more detail).
 |
| Figure 2 |
 |
| Figure 3 |
This conclusion receives further support from data on the distribution of porphyroblasts and neoblasts of olivine, the dominant mantle mineral, whose content in spinel lherzolite is $>$60%. The lengths of olivine grains were measured in thin sections in three distinct sections of xenolith samples. The size of both olivine porphyroblasts and its neoblasts in a single sample were proved to also be distributed according to the lognormal law (Figure 2 and Figure 3).
When mantle processes are modeled, the size of the olivine grains is usually assumed to be 1 mm, but even rocks of the spinel depth facies alone show significant variations in the size of their mineral grains. In some samples, the average olivine grains are 4–5 mm. The size of olivine grains notably affects the rheology of the mantle. At small sizes and low strain, deformations develop according to the diffuse creep mechanism, and the viscosity varies in this situation depending on the grain size. For example, an increase in this parameter from 10 $\mu$m to 1 mm changes the viscosity by a factor of 100 [Karato, 2008].
Our data thus suggest that the xenoliths were shaped by processes in the upper mantle, before being entrained by melts to the surface. In view of this, the petrofabrics and physical characteristics of the xenoliths were further studied in samples whose orientation relative to the axes of the respective xenoliths was known.
The petrofabrics of xenolith samples were examined in thin sections cut parallel to three mutually perpendicular planes oriented relative to the maximum elongations of the xenoliths.
 |
| Figure 4 |
When studying spinel lherzolite sample CH-1 from the Bohemian Massif in a section perpendicular to the maximum elongation of the xenolith, we have found out that mantle deformations, which are expressed in the preferred orientation of olivine grains in the xenoliths, are strongly correlated with the shapes of the xenoliths [Grachev et al., 1987]. As follows from the diagrams (Figure 4), the samples show a common petrofabric pattern in the section perpendicular to the long axis of the xenolith. The longer axis of the xenolith coincides with the dominant orientation of the [001] axes of olivine grains, with their [001] axes defining a girdle zone perpendicular to the middle axis of the xenolith. The axes [100] are parallel to the middle axis of the xenolith and lie in the flattening plane, which is perpendicular to the maximum shortening axis of the sample. The [010] girdle zone is parallel to the short axis of the sample, and the main maxima of the zone are perpendicular to the flattening plane (Figure 4). At the same time, some points in the plots for [001] and [010] are scattered, which suggests a tendency toward forming zones normal to the flattening plane and the maxima of the [100] axes. The geometry of kink-bands in olivine suggests the development of kl100] gliding systems [Grachev et al., 1987]. The type of olivine orientation corresponds to gliding along (010) [100], i.e., type A in experiments with simple shear [Kneller et al., 2005].
 |
| Figure 5 |
Analogous tendencies were identified in samples CH-25, CH-26, V-5/1, V-10/1, and V-10/2 from basalt of the Bohemian Massif and Pannonian Basin (Figure 5) [Grachev and Dobrzhinetskaya, 1987].
The flattening of xenoliths from the Bohemian Massif (Figure 5a, Figure 5b) is accentuated by the orientation of Cr-spinel grains. The fabric patterns of these samples are similar to those in sample CH-1. In [100] plots, the projections of the axes define two maxima at low angles to the flattening plane. The [001] axes make up a maximum in the central part of the diagrams. At the same time, some points of the [001] projections cluster in the peripheries of the main maximum and resemble a girdle zone normal to the flattening plane. The axes [010] also tend to project within zones, with the major maxima almost perpendicular to the flattening plane and parallel to the short axes of the xenoliths. The axes [001] of olivine are mostly parallel to the long axis of the xenolith, whereas the axes [100] are parallel to the middle axis of the xenolith, lie in its flattening plane, and are perpendicular to the short axis of the xenolith.
Xenoliths from the Pannonian Basin (Figure 5c, Figure 5d, Figure 5e) are flattened and show lineation due to the orientation of Cr-spinel grains (solid triangle indicates the projection of lineation in the [100] plots). The axes [100] cluster close to the flattening plane and define two major maxima at low angles to the lineation. Some of the [100] points are scattered around the major maxima because of the orientation of the neoblasts, which were formed during dynamic recrystallization. The axes [001] define girdle zones perpendicular to the flattening plane and lineation, which lies in this plane. At the same time, the distribution of the axes [001] has a major maximum, which occurs in the flattening plane and is parallel to the long axis of the xenolith. The [010] projections show an analogous tendency toward clustering within zones with two major maxima in the peripheral parts of the plots, perpendicular to lineation. All of the thin sections show kink-bands, whose geometry allowed us to determine the gliding planes kl00]. According to experimental data [Nicolas et al., 1973; Raleigh, 1968], kl00] gliding systems in olivine become active at temperatures of 900–1250° C.
Petrofabric analysis thus shows that girdle zone of the [010] axes tend to be oriented perpendicular to the flattening planes in which the axis [100] and flattening of the Cr-spinel lie. The [001] axes define a girdle zone, and their major maxima generally tend toward being oriented along the elongation of the xenoliths [Grachev and Dobrzhinetskaya, 1987].
Similar results were obtained in [Grachev et al., 1994; Koreshkova, 1996] when studying xenoliths (samples Tim-1, Tam-1, and L-88) in basalt of historic eruptions on Lanzarote Island; the xenoliths consist of harzburgite and dunite [Grachev, 2012].
 |
| Figure 6 |
Stereographic projection of the petrofabric elements of sample Tim-1 show a well-pronounced orientation of the olivine porphyroblasts, which are deformed and display glide dislocation in the form of kink-bands. The dominant gliding direction is [100]: 34 of the 43 measurements correspond to kl00], eight measurements correspond to (010) [100], and only one is (001) [100] [Koreshkova, 1996] (Figure 6). The [100] gliding direction, which corresponds to the direction of the plastic flow of the rock, exhibits a maximum plotting close to the lineation defined by elongate olivine grains and coinciding with the long axis of the ellipsoidal xenolith. The crystallographic axes [010] and [001] swarm within zones in a plane roughly perpendicular to the lineation. Thereby some of the projection points of [010] (which is perpendicular to the gliding plane) cluster around the short axis of the xenolith, and some of the [001] projections plot near the middle axis. The oblique setting and asymmetry of the [100] maxima relative to the lineation reflect a simple strike-slip faulting regime and correlates to sinistral strike-slip at angles of 70–80°. The strike-slip plane is thus close to the foliation plane (Figure 6). This conclusion is somewhat different from the documented dominant orientation of olivine relative to the axes of xenolith CH-1, in which [001] coincides with the long axis and [100] coincides with the short one [Koreshkova, 1996].
 |
| Figure 7 |
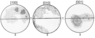
Similar to sample Tim-1, olivine porphyroblasts in sample Tam-1 define a fabric pattern typical of porphyroclastic textures. The axis [100] shows a maximum that coincides with the long axis of the xenolith and indicates the flow direction. The axes [010] and [001] lie within a zone perpendicular to the long axis of the xenolith, with the projection points clustering around the middle and short axes, respectively (Figure 7).
 |
| Figure 8 |
The orientation of olivines in sample L-88 are different from those described above: the dominant orientation of olivine in this sample is not as clear as in samples Tim-1 and Tam-1 (Figure 8). This xenolith consists of dunite and represents a refractory residue material after melting [Grachev, 2012]. Such rocks are usually thought to be formed by solidification in a magmatic chamber (magmatic underplating) and thus show no traces of mantle deformations.
The olivine orientations in xenoliths from the Baikal Rift were studied in 70 xenoliths, all of which were collected at Tumbusun-Dulga volcano in the Khamar-Daban Range to find possible petrofabric variations between xenoliths sampled at a single locality. The xenoliths were classified into two types [Moltchanova and Ratnikova, 1996].
 |
| Figure 9 |
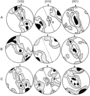
The xenoliths of type 1 are characterized by weak flattening accentuated by their Cr-spinel ($S_1$), which is perpendicular to the axis of the maximum shortening of this xenolith (Figure 9). The samples have a typical porphyroclastic texture and similar fabric patterns with clearly seen girdle distribution of the axes [010] and [001] and two maxima of the axes [100] of olivine. The arrangement of the kink-bands makes it possible to identify the \{0kl\} [100] translation systems of the olivine, which reflect the solid-state plastic flow of olivine in the experiments at temperatures of 950–1250° C. In one of the samples (Figure 9c), a (010) [100] gliding system was detected, which could be formed, according to experimental data, at $T >1250$° C
[Carter et al., 1970]. It is worth mentioning that this exactly sample hosts the greatest number of melting zones, some of which are oriented at 45° to the symmetry axis of the xenolith.
 |
| Figure 10 |
The xenoliths of the other type show more clearly pronounced Cr-spinel lineation, which is orthogonal to the maximum flattening of the samples. The projections of the axes [100] and [001] swarm within zones parallel to flattening plane $S_1$, while the axes [010] define two maxima perpendicular to the flattening plane $S_1$ (Figure 10).
Comparison of the results of petrofabric analysis shows that the two distinguished types likely reflect different deformation circumstances in the anomalous mantle of the Baikal Rift [Grachev, 1987]. The relations between the textures of xenoliths of both groups with their shapes indicate that the maximum shortening axes coincide with the dominant orientation of the axes [010] of olivine, even when these axes project within zones. The major maxima of the axes [001] are parallel to the long axes of the xenoliths, whereas the maxima of [100] are parallel to the middle axes of the samples.
Laboratory studies of the elastic characteristics ($V_p$ and $V_s$) of mantle xenoliths under a pressure of 20 kbar were launched at the Schmidt Institute in 1970 in cooperation with A. I. Levykin and then continued together with G. A. Efimova [Grachev and Levykin, 1971; Grachev et al., 1973, 1987], following the methods described in [Volarovich et al., 1975, 1977]. The velocities of $P$-waves were measured by ultrasonic pulse techniques in a piston-cylinder apparatus, with Pb as the pressure-transmitting material. Samples for the experiments were sawn off rock cubes in the form of cylinders 17.5 mm long and 22 mm in diameter. Preparatorily to the experiments, the cubes were measured under atmospheric pressure. The orientation of each of the cubes relative to the long axes of the xenoliths and the orientation of the thin sections used in petrofabric analysis were known and documented. The theoretical velocities of $s$- and $p$-waves were calculated by the generalized singular approximation technique [Bayuk and Rodkin, 1998] from data of petrofabric analysis to reveal the anisotropy of the xenoliths.
 |
| Figure 11 |
Figure 11 presents plots of $V_p$ determined for the long, middle, and short axes of sample CH-1 under pressures up to 12 kbar. The anisotropy of $V_p$ is clearly seen and systematically varies from minimum values along [010] to maximum ones along [100]. The $V_p$ curves in Figure 11 correspond to three mutually perpendicular directions: $a$ is the $V_p$ values measured along the middle axis of sample CH-1, and $b$ and $c$ are the values along the long and short axes of this sample, respectively. It can be readily seen that the experimental determined $V_p$ values exactly match petrofabric data on sample CH-1 (Figure 4), which show that the seismic anisotropy of the sample is closely related to its shape, i.e., to the orientation of the long, middle, and short axes of xenolith.
 |
| Figure 12 |
Theoretical values of the elastic properties of sample CH-1 calculated by the generalized singular approximation technique [Bayuk and Rodkin, 1998] from petrofabric data for a pressure from 5 to 20 kbar are shown in Figure 12.
 |
| Figure 13 |
The $V_p$ values determined at pressures up to 15 kbar for a number of xenoliths from a single locality in the Baikal Rift demonstrate analogous relations between the anisotropy of $V_p$ and the shape of the xenolith. Figure 13 shows experimental results on representative xenolith samples from basalt of Tumbusun-Dulga volcano. These data demonstrate systematic relations between the seismic anisotropy of the xenoliths and their shapes, i.e., the orientation of the [100], [010], and [001] axes of olivine relative to the long, middle, and short axes of the samples. Again, data on these samples show relations identified in xenolith samples from the Bohemian Massif, Pannonian Basin, and Lanzarote Island. The most interesting sample is 979/165, which shows a clearly seen melting zone approximately 0.5 mm thick, which is parallel to the long axis of this xenolith and, as was proved by petrofabric analysis, and also parallel to the axes [001] of the olivine grains. As follows from the experimental data, the decrease in the $V_p$ values in the melting zone is about 20% (Figure 13).
This result is consistent with the known fact that the wetting characteristics of crystals are different along their distinct crystallographic directions [Yoder, 1976]. It has been experimentally proved that the greater portions of wetted crystals are parallel to the axis [001] [Jung and Waff, 1998; Waff and Faul, 1992]. Theoretical and experimental studies [Yoshino et al., 2006] predict that wetting is enhanced as the square root of the melt fraction.
In the xenolith discussed above, the setting of the melting zone is thus consistent with the seismic anisotropy of this xenolith (Figure 13), i.e., the plane (010) of the olivine, which is characterized by the strongest wettability and is perpendicular to the axis [100] and the direction of shear deformation. This should result in changes in the $V_p$ values and other physical properties (thermal conductivity and viscosity) along this direction. This should also affect the dynamics of movement of the partly molten material of the anomalous mantle beneath continental rifts.
The thermal conductivity ($\lambda$) of mantle xenoliths was studied by optical scanning techniques developed by Yu. A. Popov [Popov et al., 1983] at a laboratory of the Ordzhonikidze Moscow Geological Exploration Institute. The measurements were carried out under normal thermodynamic conditions to ensure the integrity of the samples and enable later measurements. The data were measured accurate to at least 3%, which was controlled by replicate $\lambda$ measurements of a standard (quartz).
 |
| Figure 14 |
Each xenolith sample was sawn into two parts along its long axis so that the roughness of the cut surfaces did not exceed $\pm 0.5$ mm. The scan lines were marked with black enamel stripes 10 mm wide, and the measurements were carried out along two orthogonal directions: either along the long and short axes or along the long and middle ones (Figure 14). Values of $\lambda$ were thus obtained along each of the axes of the xenoliths of ellipsoidal shape. The thermal conductivity of olivine is controlled by parameters of its crystal lattice: thermal conductivity is at a maximum along [100] and at a minimum along [010] [Gibert et al., 2003, 2005; Tommasi et al., 2001]. Thermal conductivity also depends on the size of the olivine grains, i.e., the contribution of the olivine neoblasts to $\lambda$ is insignificant.
 |
| Table 1 |
The thermal conductivity of studied xenoliths is characterized by significant anisotropy along various axes of the samples (Table 1). In all samples, $\lambda$ along the middle axis, i.e., parallel to [100], is always greater than this parameter along the short axis and long axis. The thermal conductivity in the partial melting zone (sample 979/104) is 1.9 W/m K.
Our data on the thermal conductivity of mantle xenoliths along their long, middle, and short axes proves that $\lambda$ depends on the shapes of the samples, and these relations can be explained by the dominant orientation of the crystallographic axes of the olivine, whose content in these samples exceeds 60%.
The anisotropy of thermal conductivity also depends on the pyroxene content in the xenoliths, with an increase in this parameter decreasing the anisotropy [Tommasi et al., 2001], but does not principally modify these relations.
The dependence of the thermal conductivity anisotropy of xenoliths on their shape is thus proved without any a priori assumptions concerning the petrofabrics of the samples.
As follows from experimental results, the seismic anisotropy of the upper mantle can be explained by either a preferred orientation of the axis [100] of olivine, which coincides with flow direction of the material [Nicolas and Christensen, 1987; and several others], or by the dominant orientation of the partial melting zones (OMP model in [Kendall, 2006]). In the latter situation, an important role (along with the degree of partial melting, which is no lower than 2%) is also played by the morphology of these zones [Schmeling, 1985].
Our results indicate that the development of the seismic anisotropy of our xenolith samples predetermined by contributed by both of these processes. The arrangement of the melting zones is consistent with the anisotropic fabric of the xenoliths and hence provides further support to the hypothesis that the anisotropy of the xenoliths depends on their shapes and was in situ produced in the mantle before the xenoliths were captured by melt.
The degree of partial melting should control the viscosity of the mantle material and, hence, also the spreading velocity of the anomalous mantle material beneath continental rifts. Because the degree of partial melting is not constant, it is reasonable to suggest that the horizontal spreading velocity of mantle material should also vary, and this should bring about large scale zones of plastic shearing along which mantle material flows.
Our results are important for understanding processes in the anomalous mantle of continental rifts. Isotopic-geochemical data indicate that volcanism in the Baikal Rift is affected by a mantle plume [Grachev, 1998; Johnson et al., 2005], and seismic tomography data suggest the occurrence of low-velocity mantle to a depth of 600 km [Mordvinova et al., 2000; Zhao et al., 2006].
Models of the ascent of a mantle plume suggest that it should be fragmented into a number of cells when approaching the bottom of the solid crust [Grachev et al., 1998]. The mantle cannot be fragmented if no partial melting zones are formed in it. As follows from data on the xenoliths, these zones are arranged in the samples parallel to the long axes of the xenoliths and [001] of their olivine. The setting of the melting zone is thus consistent with the seismic anisotropy of the xenolith, i.e., the plane (010) of the olivine is perpendicular to the axis [100] and the direction of shear deformations, and this should result in changes in the $V_p$ velocity, thermal conductivity and viscosity [Grachev and Malevskii, 1988].
Babuska, V., J. Plomerova, J. Sileny (1984), Large-scale oriented structures in the subcrustal lithosphere of Central Europe, Ann. Geophys., 2, p. 649–662.
Bayuk, I. O., M. V. Rodkin (1998), Physical and mathematical modeling of the elastic properties and electrical conduction of rocks by the OSA method, Physics of the Earth, no. 12, p. 3–14.
Carter, N. L., H. G. Ave`Lallement (1970), High-temperature flow dunite and peridotite, Bull. Geol. Soc. Amer., 81, p. 2181–2202, doi:10.1130/0016-7606(1970)81[2181:HTFODA]2.0.CO;2.
Christensen, N. L. (1966), Elasticity of ultrabasic rocks, J. Geophys. Res., 71, p. 5921–5931, doi:10.1029/JZ071i024p05921.
Gass, I. G., S. J. Lippard, A. W. Shelton Eds. (1984), Ophiolites and Oceanic Lithosphere, 413 pp., Geol. Soc., Oxford.
Gibert, B., F. R. Schilling, A. Tommasi, D. Mainprice (2003), Thermal diffusivity of olivine single-crystals and polycrystalline aggregates at ambient conditions – a comparison, Geoph. Res. Lett., 30, p. 2172, doi:10.1029/2003GL018459.
Gibert, B., F. R. Schilling, K. Gratz, A. Tommasi (2005), Thermal diffusivity of olivine single crystals and a dunite at high temperature: Evidence for heat transfer by radiation in the upper mantle, Physics of the Earth and Planetary Interiors, 151, p. 129–141, doi:10.1016/j.pepi.2005.02.003.
Grachev, A. F. (1987), Rift Zones of the Earth. 2nd edition, 287 pp., Nedra, Moscow.
Grachev, A. F. (1998), Khamar-Daban is a hotspot in the Baikal Rift: chemical geodynamics evidence, Physics of the Earth, no. 3, p. 3–28.
Grachev, A. F. (2012), MORB-like mantle beneath Lanzerote Island, Canary Islands, Rus. J. Earth. Sci., 12, p. ES3004, doi:10.2205/2012ES000515.
Grachev, A. F., L. F. Dobrzhinetskaya (1987), Textural anisotropy of mantle xenoliths in Neogene volcanics in Central Europe and its importance for interpreting the azimuthal seismic anisotropy of the lithosphere, Deep Xenoliths and the Structure of the Lithosphere, p. 178–193, XENOLITH Project, Moscow.
Grachev, A. F., A. I. Levykin (1971), New data on the nature of low velocity zone of the rift zones, Abstract of XV Assambly of IUGG, p. 11, Nauka, Moscow.
Grachev, A. F., A. V. Malevskii (1988), On the viscosity anisotropy of the anomalous mantle, Dokl. AN SSSR, 303, no. 4, p. 830–833.
Grachev, A. F., A. Arana, A. Aparicio (1994), State and composition of the upper mantle beneath the Canary Islands, Teide Laboratory Volcano Project, Progress Report, Contract: EVSV-CT93-0283, p. 21–28, Teide Laboratory, Madrid.
Grachev, A. F., E. I. Blumstein, E. P. Sokolova, A. I. Levykin (1973), Lherzolite nodules in alkaline basalts of the north-eastern part of the Baikal rift, Dokl. AN SSSR, 211, no. 2, p. 445–447.
Grachev, A. F., V. V. Nikolaichik, V. P. Trubitsyn (1985), On the nature of the geometrically regular shapes of ultramafic xenoliths in basalt and patterns of their size distribution, Dokl. AN SSSR, 285, no. 6, p. 1433–1435.
Grachev, A. F., et al. (1987), On the compositional, textural, and physical heterogeneity of a single spinel lherzolite sample, Deep Xenoliths and the Structure of the Lithosphere, p. 8–30, XENOLITH Project, Moscow.
Grachev, A. F., V. I. Kondaurov, A. V. Konyukhov, V. A. Magnitsky (1998), On some numerical solutions of the problem of mantle diapir emplacement in the lithosphere, Physics of the Earth, no. 11, p. 3–10.
Hess, H. H. (1964), Seismic anisotropy of the uppermost mantle under oceans, Nature, 203, p. 629–631, doi:10.1038/203629a0.
Johnson, J. S., S. A. Gibson, R. N. Thompson, G. M. Nowell (2005), Volcanism in the Vitim Volcanic Field, Siberia: Geochemical Evidence for a Mantle Plume Beneath the Baikal Rift Zone, J. Petrol., 46, p. 1309–1344, doi:10.1093/petrology/egi016.
Jung, H., H. S. Waff (1998), Olivine crystallographic control and anisotropic melt distribution in ultramafic partial melts, Geoph. Res. Lett., 25, p. 2901–2904, doi:10.1029/98GL02177.
Karato, S. (2008), Deformation of Earth Materials: Introduction to the Rheology of the Solid Earth, 462 pp., Cambridge Univ. Press, Cambridge, UK, doi:10.1017/CBO9780511804892.
Kendall, J.-M., S. Pilidous, D. Keir, I. Bastow, G. Stuart, A. Ayele (2006), Mantle upwellings, melt migration and the rifting of Africa: insights from seismic anisotropy, The Afar Volcanic Province Within the East African Rift System, G. Yirgu, C. J. Ebinger, P. K. H. Maguire (Eds.), Special Publications, 259, p. 55–72, Geological Society, London, doi:10.1144/gsl.sp.2006.259.01.06.
Kluegel, A. (1998), Reactions between mantle xenoliths and host magma beneath La Palma (Canary Islands): Constraints on magma ascent rates and crustal reservoirs, Contrib. Mineral. Petrol., 131, p. 237–257, doi:10.1007/s004100050391.
Kneller, E. A., P. E. van Keken, S. Karato, J. Park (2005), B-type olivine fabric in the mantle wedge: Insights from high-resolution non-Newtonian subduction zone models, Earth and Planet. Sci. Lett., 237, p. 781–797, doi:10.1016/j.epsl.2005.06.049.
Kolmogorov, A. N. (1985), Probability Theory and Mathematical Statistics, 264–266 pp., Nauka, Moscow.
Koreshkova, M. Yu. (1996), Petrology of mantle xenoliths in alkaline basalts of the Lanzerote Island, Canary Islands, Vestnik St.-Petersburg University, 3, p. 65–70.
Moltchanova, T. V., G. I. Ratnikova (1996), Texture inhomogeneity of xenoliths from Cainozoic basalts of the Khamar-Daban Ridge (Tumbusun-Dulga volcano), Ultrabasic Xenoliths in Basalt Magmas, p. 100–109, Nauka, Moscow.
Mordvinova, V. V., L. P. Vinnik, G. L. Kosarev, S. I. Oreshin, A. V. Treusov (2000), Teleseismic tomography of the Baikal Rift lithosphere, Dokl. Earth Sciences, 372, no. 4, p. 716–720.
Morin, D., L. Corriveau (1996), Fragmentation processes and xenolith transport in a Proterozoicminette dyke, Grenville Province, Quebec, Contrib. Mineral. Petrol., 125, p. 319–331, doi:10.1007/s004100050225.
Nicolas, A., N. I. Christensen (1987), Formation of anisotropy in upper mantle peridotites – a review, Structure and Dynamics of the Lithosphere–Astenosphere K. Fuchs, C. Froidevaux (Eds.), System. Geodynamics Series, vol. 16, p. 111–123, AGU, USA.
Nicolas, A., F. Boudier, A. M. Boullier (1973), Mechanisms of flow in naturally and experimentally deformed peridotites, Amer. J. Sci., 273, p. 853–876, doi:10.2475/ajs.273.10.853.
Popov, Yu., V. G. Semenov, V. M. Korostelev, V. V. Berezin (1983), Remote evaluation of the thermal conductivity of rocks using a mobile heat source, Physics of the Earth, no. 7, p. 86–93.
Raleigh, C. B. (1968), Mechanisms of plastic deformations of olivine, J. Geophys. Res., 73, p. 5391–5406, doi:10.1029/JB073i016p05391.
Schmeling, H. (1985), Numerical models on the influence of partial melts on elastic, anelastic and electrical properties of rocks. Part I: elasticity and anelasticity, Phys. Earth Planet. Inter., 41, p. 34–57, doi:10.1016/0031-9201(85)90100-1.
Spera, F. J. (1984), Carbon dioxide in petrogenesis III: role of volatiles in the ascent od alkaline magma with special reference to xenolith-bearing mafic lavas, Contrib. Mineral. Petrol., 88, p. 217–232, doi:10.1007/BF00380167.
Tommasi, A., B. Gibert, U. Selpold, D. Mainprice (2001), Anisotropy of thermal diffusivity in the upper mantle, Nature, 411, p. 783–786, doi:10.1038/35081046.
Verma, R. K. (1960), Elasticity of several high-density crystals, J. Geophys. Res., 65, p. 757–766, doi:10.1029/JZ065i002p00757.
Volarovich, M. P., E. I. Bayuk, F. M. Levitova (1977), A technique for simultaneous measuring the elastic properties and density of rocks at 20 kbar, Leipzig Gerlands Beitr$\ddot{a}$ge zur Geophysik, 86, p. 69–78.
Volarovich, M. P., E. I. Bayuk, G. A. Efimova (1975), Elastic Properties of Minerals Under High Pressures, 131 pp., Nauka, Moscow.
Waff, H. S., U. H. Faul (1992), Effects of crystalline anisotropy on fluid distribution in ultramafic partial melts, J. Geoph. Res., 97, p. 9003–9014, doi:10.1029/92JB00066.
Yoder, H. S. Jr. (1976), Generation of Basaltic Magma, National Academy of Sciences, Washington, D.C.
Yoshino, T., T. Matsuzaki, S. Yamashita, T. Katsura (2006), Hydrous olivine unable to account for conductivity anomaly at the top of the asthenosphere, Nature, 443, p. 973–976, doi:10.1038/nature05223.
Zhao, Dapeng, Jianshe Lei, Tomofumi Inoue, Akira Yamada, Stephen S. Gao (2006), Deep structure and origin of the Baikal rift zone, Earth and Planet. Sci. Lett., 243, p. 681–691, doi:10.1016/j.epsl.2006.01.033.
Received 29 March 2016; accepted 1 April 2016; published 12 April 2016.


Citation: Grachev A. F. (2016), Anisotropy of elastic properties and thermal conductivity of the upper mantle -- a case study of xenoliths shape: Evidence from xenoliths in basalts in North Eurasia, Russ. J. Earth Sci., 16, ES2002, doi:10.2205/2016ES000566.
Copyright 2016 by the Geophysical Center RAS.