
RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 15, ES4004, doi:10.2205/2015ES000559, 2015
B. P. Nikolov1, J. I. Zharkikh1, A. A. Soloviev1,2, R. I. Krasnoperov1, S. M. Agayan1
1Geophysical Center of Russian Academy of Sciences, Moscow, Russia
2Also at Institute of Physics of the Earth of Russian Academy of Sciences, Moscow, Russia
.Spatial data handling and analysis is one of the most important trends in modern computer oriented geophysics and geology. This article describes a software complex designed for integration of geodata analysis algorithms in a unified geoinformation environment. The developed software system provides access to an extensive geodatabase on Earth sciences and constantly updated catalog of algorithms and requires only a Web browser and Internet connection. This paper contains a mathematical description of some methods of data mining and data analysis, which have been already incorporated into the system. The discussed results also include the application of the algorithms, arranged in a database, to geological and geophysical data within the GIS environment.
With the development of science and technology, intensity of geodata accumulation increases. It causes difficulties in the exchange of geophysical knowledge between researchers and users. Implementation of modern and efficient geoinformation technologies can simplify the process of geodata management, analysis and exchange. It also provides quick and efficient solutions of a vast majority of specific tasks.
Modern Geographic Information System (GIS) is a set of technical, software and information resources, which provide input, storage, processing, mathematical and cartographic modeling and graphical representation of georeferenced data and allow performing their correlation with attribute data (https://www.itc.nl/library/papers_2009/general/Principles GIS.pdf).
The concept of GIS is layer-by-layer organization of spatial data implying that data of the same type are usually grouped into layers; multiple thematic layers form a map. GIS allows working only with data layers, which include information required for a specific task.
Nowadays there is a number of Web-based systems that provide a variety of ways for processing geophysical and geological data. For example, GES DISC (Goddard Earth Sciences Data and Information Services Center) Interactive Online Visualization and Analysis Infrastructure (GIOVANNI) [GIOVANNI: [website], URL: http://giovanni.sci.gsfc.nasa. gov/giovanni/], created by NASA, allows access to various data processing procedures as well as visualization of remote sensing data. The Institute of Computing Technology in cooperation with the Institute of Geology and Mineralogy of the Siberian Branch of the Russian Academy of Sciences developed a tool for searching, processing and analyzing geodata [Shokin et al., 2007]. This approach is a combination of GIS and Web technologies. Other examples of such systems are presented in [Alekseev et al., 1998; Galin et al., 2003; Okladnikov et al., 2013; KNMI Climate Explorer, URL: http://climexp.knmi.nl/]. The existing GIS systems, including Web-based ones, provide access to a large diversity of data arrays on Earth sciences. Nevertheless, these systems usually do not allow a user to process, visualize and analyze data received from various sources and apply GIS-oriented, general-purpose algorithms.
Contemporary study of internal structure, evolution and dynamics of the Earth using information on seismic sounding, gravity and magnetic anomalies, etc. is increasingly accompanied by computer simulation and analysis. A lot of new mathematical methods of interpretation and modeling of geophysical fields and other processes have been developed and continue to develop. Such methods and data processing algorithms are being developed at the Geophysical Center of RAS (GC RAS) and Schmidt Institute of Physics of the Earth of RAS, as well as many other Russian and foreign scientific institutions.
At the same time the implementation and application of algorithms for geodata analysis is a very demanding task. The creation, filling and support of databases and servers require highly skilled professionals, as well as other resources. All this causes the necessity of integration of geodata and algorithms of their processing and intellectual analysis into a single environment available online [Berezko et al., 2008, Beriozko et al., 2011; Lebedev and Beriozko, 2009].
Centralized catalogue of geodata processing algorithms, which will be discussed in the article, is a subsystem of GIS responsible for access to specific methods of geodata processing performed centrally on a server.
GIS server should include the necessary software and hardware to provide execution of algorithms and transmission of the results to user, as well as storage of geodata and processing results [Lebedev and Beriozko, 2009]. A significant advantage of such environment is the ability of creating a unified library of geoprocessing methods. The GIS, which allows integrating applications for geoprocessing algorithms, provides the functionality to develop new algorithms and include them in the unified and constantly extending catalogue. This allows researchers to focus on the mathematical implementation of such algorithms and the results of their application in a unified GIS environment.
In contrast to executing the algorithms on a local computer, the proposed technology of the server-based catalogue has the following advantages:
Today there are many highly specialized GIS solutions for a diverse range of tasks, but they are quite demanding on computer performance. Often for each specific case a sophisticated approach is needed, and it requires the user to have knowledge in a specific area. Solving this problem requires a unified system, which integrates both geodata and algorithms that could be applied to them.
The developed software complex designed for integration of geodata analysis algorithms includes the following components:
The elaborated system includes: services for data processing based on REST API technology and a Web application based on [ArcGIS API for JavaScript. The Web application was designed to send tasks to the server, check the status of their execution, retrieve the results in asynchronous mode, and visualize the obtained results by adding them on the map.
With the development of science and technology there is a rapid increase in volume of geophysical data. In parallel, a transition from the presentation of the results in an analog form to digital format takes place in many data centers all over the world. This had an impact on the growth of digital methods for data analysis and development of discrete mathematics.
One of the areas of discrete mathematics is intellectual data processing, which involves modeling of human ability to analyze information. Indeed, an expert can effectively carry out clustering of objects, highlight and estimate anomalies and find signals on records by eye with the condition of moderate-size data sets of maximum three dimension. However, with the increase of data volume and dimensions and hence the volume of the calculations, people lose this ability. This paper refers to the possibility of modeling a human ability to analyze data with the subsequent transfer of this knowledge in order to process large amounts of information (e.g., [Gvishiani et al., 2010; Soloviev et al., 2013]).
Arrays of digital data on geology and geophysics as well as other Earth observations are characterized by great noise pollution. Such data often have sufficiently approximate and fuzzy nature. This makes very important the role of an expert's competence in analysis of such information. The mathematical description of fuzzy expert's estimates can be obtained using fuzzy math and fuzzy logic [Kaufmann, 1975; Zelinskiy et al., 2014].
Fuzzy logic is an apparatus that takes into account both fuzzy data and expert mindset. It is the basis of the approach to geological and geophysical data analysis by methods of artificial intelligence. Using this approach, the discrete analogs of the fundamental concepts of classical mathematical analysis, such as limit, continuity, monotony, have been formally defined in the framework of Discrete Mathematical Analysis (DMA) (e.g., [Gvishiani et al., 2008]).
Fuzzy logic and fuzzy mathematics form the DMA approach. It represents a set of algorithms with a single formal basis and a universal character. In particular, DMA includes a series of neo-clustering algorithms, which allow determining dense object condensations in multidimensional arrays and define their morphology (e.g., linear and ring structures), as well as the algorithms of anomaly recognition within noised time series. DMA has already found many successful applications in studying and recognizing anomalies in geological, geophysical and geodynamic data [Agayan and Soloviev, 2004; Bogoutdinov et al., 2010; Gvishiani et al., 2008, 2010, 2013, 2014; Sidorov et al., 2012; Soloviev et al., 2005, 2009, 2012a, 2012b, 2013; Zelinskiy et al., 2014].
Some basic mathematical constructs underlying the DMA algorithms are given below.
Fuzzy comparison $n(a,b)$ of the real numbers $a$ and $b$ measures in alternating scale interval $[-1;1]$ a degree of superiority $b$ over $a$:
\begin{eqnarray*} n(a,b)= \mathrm{mes} (a < b) \in [-1;1] \end{eqnarray*}where $a$, $b$ – real numbers, $n(a,b)$ – fuzzy binary relation on $\mathbb{R}$.
Thus, $n$ can be any function $f(a,b)$, $f : R \to [-1,1]$, increasing with respect to $b$ for fixed $a$ and decreasing with respect to $a$ for fixed $b$ with additional boundary conditions:
\begin{eqnarray*} \forall a: \lim_{b \to \pm \infty} f(a,b) = \pm 1 \end{eqnarray*} \begin{eqnarray*} \forall a: \lim_{a \to \pm \infty} f(a,b) = \mp 1 \end{eqnarray*} \begin{eqnarray*} \forall a: \lim f(a,a) = 0 \end{eqnarray*}where $a$, $b$ – real numbers. An example of such a function (1):
\begin{equation} \tag*{(1)} n(a,b) = \frac{b-a}{1+|b-a|} \end{equation}where $a$, $b$ – real numbers.
 |
| Figure 1 |
Figure 1 is a plot illustrating the formula (1) for a fixed $a=0$ and variable $b$.
The next step, after determining the fuzzy comparison of numbers $n(a,b)$, is its extension to concepts of fuzzy comparisons $n(a,A)$ and $n(A,a)$ of an arbitrary number $a\in \mathbb{R}$ with arbitrary weighted, finite set of numbers $A$.
\begin{eqnarray*} A= \{ (a_i, w_i)|_1^N, \quad a_i \in R, \quad w_i >0 , i= 1 \ldots N\} \end{eqnarray*} \begin{eqnarray*} w_i >0, \; i= \{1 \ldots N\} \end{eqnarray*}where $a_i$ is the $i$-th element of the set $A$; $w_i$ is weight of the $i$-th element; $N$ is number of elements in the set $A$.
This expansion is ambiguous, and each variant formalizes the concept of "large (small) with respect to $A$ (modulo $A$)" in its own way.
Fuzzy comparison $n(a,A)$ and $n(A,a)$ should be treated as a function of membership to fuzzy concepts "to be small modulo $A$" and "to be great modulo $A$" on $\mathbb{R}$:
\begin{eqnarray*} n(a,A)= \mathrm{mes} (a < A) \end{eqnarray*}\begin{eqnarray*} n(A,a)= \mathrm{mes} (A < a) \end{eqnarray*}
where $a$ is real number; $A$ is weighted set of real numbers.
The DMA algorithms typically use the binary expansion:
\begin{eqnarray*} n(a,A)= \frac{\Sigma_{i=1}^N n(a,a_i)w_i}{\Sigma_{i=1}^N w_i} \end{eqnarray*}\begin{eqnarray*} n(A,a)= \frac{\Sigma_{i=1}^N n(a_i,a)w_i}{\Sigma_{i=1}^N w_i} \end{eqnarray*}
where $a_i$ is element of $A$; $w_i$ is weight of the $i$-th element; $N$ is the number of elements of the $A$.
Let $A= \{ (a_i, w_i) |_1^N \}$ be a positive weighted distribution and $p \in \mathbb{R}$, then the classical Kolmogorov mean (or Quasi-arithmetic mean) [Aivazyan, 1989] would be called the structure of the following form (2):
\begin{equation} \tag*{(2)} K(A,p)= \sqrt[p]{ \frac{\Sigma_{i=1}^N a_i^p w_i}{\Sigma_{i=1}^N w_i}} \end{equation}where $A$ is weighted set of real numbers, $a_i$ is element of $A$; $w_i$ is weight of the $i$-th element; $N$ is the number of elements of the $A$; $p$ is real number.
The function (2) is continuous, strictly increasing and has limits at $\pm \infty$:
\begin{eqnarray*} \lim_{p\to - \infty} K(A,p) = \min A \end{eqnarray*}\begin{eqnarray*} \lim_{p\to \infty} K(A,p) = \max A \end{eqnarray*}
Studies show that the Kolmogorov mean with the parameter $p \in [-2; 3]$ models well the concept of "small distance" in $A$.
GIS-oriented algorithm database includes both classical (such as $K$-means) and new clustering algorithms designed at the GC RAS. Among the latter, the following were included in the algorithmic base:
A brief description of each of them is given below.
Algorithm "Monolith" is designed for recognition of dense subsets of the elements in metric spaces.
Let $X$ be the finite set. $A, \; B \ldots$, and $x, \; y \ldots$ are respectively subsets and points in $X$. Let us introduce the definition of density. The density $P$ of the set $X$ is a mapping which transforms $2^X \times X$ into a segment $[0,1]$ that increases in the first argument:
\begin{eqnarray*} P(A,x) = P_A(x) \end{eqnarray*} \begin{eqnarray*} \forall x \in X: A \subseteq B \to P_A(x) \leq P_B(x) \end{eqnarray*}Thus, $P_A(x)$ is density of the subset $A$ at point $x$. We understand this value as a measure of limit of points $x$ to the subset $A$. Points $x$ with sufficiently high density are considered to be the limit of $A$ [Agayan et al., 2011]:
\begin{eqnarray*} P_A(x) \geq \alpha \end{eqnarray*}where $\alpha \in [0,1]$ is density level.
Dense set $A(\alpha)$ will consist of those points $x$, which satisfy the condition:
\begin{eqnarray*} A(\alpha) = \{ x \in X: P_{A(\alpha)} (x) \geq \alpha \} \end{eqnarray*}At all points of the subset complement density is smaller than $\alpha$.
To determine the density at any point we consider a punctured neighborhood of $x$ with radius $r$:
\begin{eqnarray*} D_A' (x,r) = \{ y \in A: 0 < d (x,y) \leq r \} \end{eqnarray*}We divide the punctured neighborhood into $m$ intersecting rings:
\begin{eqnarray*} D_A' (x,r) = \bigcup_{n=1}^m S_n \end{eqnarray*}where $S_n$ is defined as:
\begin{eqnarray*} S_n = \{ y \in A: r_{n-1} < d (x,y) \leq r_n \} \end{eqnarray*}and the radii satisfy the condition:
\begin{eqnarray*} 0= r_0 < \ldots < r_m =r \end{eqnarray*}Weights $\psi_n$, $n = 1, 2 \ldots m$, $1 \geq \psi_1 \geq \ldots \geq \psi_m > 0$, are associated with each ring and defined by the formula:
\begin{eqnarray*} \psi_n= \left( 1 - \frac{n}{m+1} \right)^k, \qquad k>0 \end{eqnarray*}The density of subset $A\subseteq X$ at point $x \in X$ will be the ratio of the sum of weights of non-empty rings to the sum of the weights of all rings [Agayan et al., 2011]:
\begin{eqnarray*} P_A(x) = \frac{ \sum \limits_{n=1, S_n \neq \emptyset}^m \psi_n}{ \sum \limits_{n=1}^m \psi_n} \end{eqnarray*}Algorithm "Rodin-2" is designed for recognition of dense areas in finite metric spaces. Basically it uses structures of Kolmogorov mean [Aivazyan, 1989] and "fuzzy comparison" [Gvishiani et al., 2008].
Input data for the algorithm include:
Let us introduce the following notations:
1) Let $D$ be a set of distances $d(x, \bar{x})$ from point $x$ such that $x \neq \bar{x}$. $\bar{x} \in X$:
\begin{eqnarray*} D = \{ d(x, \bar{x}), \; x \neq \bar{x}, \; \bar{x} \in X \} \end{eqnarray*}where $d$ is a distance between two elements of $X$; $x$ and $\bar{x}$ are elements of $X$.
2) Let $\delta_x$ be a measure of proximity for the point $x \in X$ with respect to the space $X$:
\begin{eqnarray*} \delta_x = K(D,p) \end{eqnarray*}where $D$ is a set of distances, $p$ is a real number.
3) Let $\Delta$ be the set of all $\delta_x$ for $x \in X$:
\begin{eqnarray*} \Delta= \{ \delta_x , x \in X \} \end{eqnarray*}where $x$ is the element of the $X$, $\delta_x$ is a measure of proximity for the point $x \in X$ with respect to the space $X$.
We can distinguish the following main steps of the algorithm "Rodin-2":
DPS and modified DPS algorithms. The Discrete Perfect Sets (DPS) algorithm represents the process of the construction of $\alpha$-shell $A(\alpha) = A_p(\alpha|X)$ for manifold A within universe $X$ using density $P$ [Agayan et al., 2014]. DPS algorithm was created at GC RAS as a new approach to discrete data analysis and a part of DMA. The main idea of DPS algorithm involves recognition of dense areas with a certain density level $\alpha$, which belongs to interval $[0, 1]$, within a finite manifold $X$. There are two user-adjustable parameters: $\omega \; (\omega < 0)$ for closeness radius determination and $\beta\in [0, 1]$, which is required for density level determination.
As a result, the algorithm forms a set of points $X(\alpha(\beta, \omega))$, which are $\alpha$-dense. The obtained sets of points will be called clusters. At every iteration of the algorithm except the first one, at which the initial set of points is analyzed, clustering is performed only for complement $X\setminus X (\alpha(\beta, \omega))$. Application of DPS algorithm for recognition of dense areas provides a union of clusters, obtained at every iteration [Agayan et al., 2014].
Determination of dense areas requires the knowledge of closeness radius. Suppose that nontrivial distances $d$ between every two points within space $X$ are given. Let us denote the set of such points as $R$. Using a generalized form or Kolmogorov mean and knowing distances between separate elements of the set, one can obtain a generalized distance.
\begin{eqnarray*} R(X) = \{ d(x,y): x,y \in X, \; d(x,y) \neq 0 \} \end{eqnarray*}Closeness radius is determined using a particular form of the generalized mean, namely power mean (3):
\begin{equation} \tag*{(3)} r= \left( \frac{\sum\limits_{ d \in R(X)}d^\omega}{|R(X)|} \right)^{1/\omega} \end{equation}where $r$ is unknown closeness radius, $d$ is a distance between two points from the $X$, $\omega$ is a negative number; $|R(X)|$ is power of the set $R$.
For every point $x$ from the set $X$ let us consider a sphere with center in $x$ and radius $r$:
\begin{eqnarray*} D(x,r) = \{ y \in X: d(x,y) \leq r \} \end{eqnarray*}For each point $x \in X$ let us determine the sum, which takes into account points from $D(x, r)$:
\begin{eqnarray*} N_X (x,r) = \sum\limits_{y \in D(x,r)} \left( 1 - \frac{d(x,y)}{r} \right)^\rho \end{eqnarray*}where $\rho \geq 0$.
The maximum of such sums for all points $x \in X$ is defined as:
\begin{eqnarray*} C(X, r) = \max_{x \in X} N_X (x,r) \end{eqnarray*}In the same way, for each $x \in X$ let us determine the sum of the form (4), which takes into account points from intersection of a sphere $D(x, r)$ with subset $A$.
\begin{equation} \tag*{(4)} N_A (x,r) = \sum\limits_{y \in D_A(x,r)} \left( 1 - \frac{d(x,y)}{r} \right)^\rho \end{equation}In (4) $D_A (x, r)$ is defined as: The maximum of such sums for all points $x \in X$ is defined as:
\begin{eqnarray*} D_A(x, r) = D(x, r) \bigcap A \end{eqnarray*}Density of subset $A\subseteq X$ in a point is determined by:
\begin{eqnarray*} P_A(x) = \frac{N_A (x,r)}{C(X,r)} \end{eqnarray*}For dense areas separation we have to determine the level of density $\alpha$, which affects the algorithm result. To do this the fuzzy comparison technique is applied. The parameter $\alpha$, which is to be determined, is considered as a solution of the corresponding equation. The obtained densities for every point $P_A(x)$ will be considered as a set of numbers, denoted as $P_A(X)$. The result of fuzzy comparison will be the parameter $\beta$ with a user-assigned value (5):
\begin{equation} \tag*{(5)} n(P_A (X),\alpha) = \frac{\sum\limits_{x \in X} n(P_A (X),\alpha)}{|X|} = \beta \end{equation}In the present research we used the following construction as a fuzzy comparison:
\begin{eqnarray*} n(P_A (x),\alpha) = \frac{ \alpha - P_A (x)}{\max (P_A (x),\alpha)} \end{eqnarray*}The solution of equation (5) was found by means of bisection method.
Determination of dense areas in the Modified DPS algorithm is performed in the same way as in the conventional DPS (density is calculated in every point and only points with density above or equal to level $\alpha$ are taken into account). However, the way of density $P$ determination is different.
Again, we consider elements $x \in X$ and calculate distances $d$ between each two elements of the set $X$. For every element we obtain a set of distances $R'$ of dimension $N$, where $N$ is the total number of elements in the set $X$. Using the elements of the set $R'$ we calculate Kolmogorov mean for each point of the set $X$. Thereby, a number $\bar{d}(x)$ is assigned to every element from the $X$, which is a power mean of distances from the considered element to the others:
\begin{eqnarray*} \bar{d}(x)= \left( \frac{\sum \limits_{ y \in X} d(x,y)^\omega}{|R'|} \right)^{1/\omega} \end{eqnarray*}For every element $x \in X$ let us consider a sphere with center in $x$ and fixed radius $r$ calculated according to (3). Let us determine the sum, which takes into account points from intersection of a sphere $D(x, r)$ with subset $A$:
\begin{eqnarray*} S_A (x, r) = \sum \limits_{ y \in D_A(x,r)} (\bar{d}(y))^{\tau} \end{eqnarray*}where $\tau \geq 0$.
Consequently, the density of subset $A\subseteq X$ in $x \in X$ is defined in the following way:
\begin{eqnarray*} P_A (x) = \frac{S_A (x,r)}{\max\limits_{x \in X} (S_A (x,r))} \end{eqnarray*}
User-system interaction is performed by means of a Web client, which includes a list of selected algorithms, a map, and layer management tools. The Web client interacts with the Web server by means of JavaScript and REST API. It is also used for up-to-date data selection and retrieval from the server. As an example, let us consider a vast geodatabase on Earth sciences, which is available via the geoportal of the Geophysical Center of RAS (http://gis.gcras.ru).
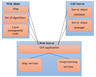 |
| Figure 2 |
Geoprocessing services is a powerful method for exposing online analytic capabilities, including the problem of spatial data processing (geoprocessing tasks). Geoprocessing tasks provide unique opportunities for geodata manipulations: from data sets processing (creating subsets, converting data sets into required formats) to performing analysis for solving numerous organizational and planning problems within various areas of human activity. The client requests to execute a task and provides the input parameters. The server executes the task and returns the output values to the client. Each geoprocessing task has its own parameters and supports either the Execute Task or Submit Job operation based on the execution type of the parent geoprocessing service. The access URL for a geoprocessing task is
used to access its page. The geoprocessing task parameters are its inputs and outputs, and depend on the actual task based on its geoprocessing functionality. Each parameter has a set of properties that provide information such as name, data and parameter type.
The client can access the system via the user application. The client application contains a list of data and a set of algorithms and applications stored on the GC RAS server. The user can choose a particular data layer and apply the selected processing algorithm indicating the values of the free parameters of the chosen algorithm. After an appropriate selection the client sends a request in JSON format, which transmits information on the user's request to the server via REST API. It sets a geoprocessing task, which has a unique identifier, assigned to it.
The client can periodically send requests through the URL and determine the status of the job. The server response for job status request includes the unique identifier (jobId) and task status (jobStatus) messages from geoprocessing service depending on the message level settings. If the job is completed successfully (jobStatus = esriJobSucceeded), the server creates new resources for the input and output parameters which can be accessed using a URL. The server response of the status request includes information on the URL for inputs and results. At the end of successful task completion, the client must send a request to receive each output parameter.
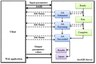 |
| Figure 3 |
Figure 3 shows the generalized diagram of the client and server interaction, as described above.
The result URL is
http://$\!<$url-task$>\!$/results/$<$parameter-name$>$, the inputs URL is
http://$<$url-task$>$/inputs/$<$para meter-name$>$. The response from these resources will be the parameter value in any JSON/KML/AMF/HTML output format depending on the client's choice.
If the geoprocessing service has been published with the option "View results with a map service", the geoprocessing server creates an accompanying map service for output parameters after successful completion of the task.
It can be added to Web applications similar to adding dynamic map services. However, if certain output data has to be excluded, the visibility of the corresponding layers can be turned off. Layer objects in the resulting map service may be added independently as object layers of client side of the Web application.
Client-side object layer will dynamically draw and display objects in the client. In the case of large volumes of data output, one can specify the object layer parameter, which enables dynamic loading of objects only for the current extent of the map in the Web application [ArcGIS Resources: [website], URL: http://resources.arcgis.com/en/help/].
As a server platform for the implementation of designed software package ESRI ArcGIS for Server was used. This product is a software package designed for geographic information exchange within the organization and on the Internet by means of Web services for receiving and processing information. Services can be used in any application or device that can address the Web service using the HTTP protocol [ArcGIS Resources: [website], URL: http://resources.arcgis. com/en/help/]. ArcGIS for Server contains the Administration Manager application and API, which can be used to configure the server settings and safety rules, logging, etc.
For developing and debugging necessary software components, ArcGIS for Server 10.2.2 package was installed and configured on a local computer running Windows 7. This program simulates the full capabilities of the server within a single local computer. It provides client interaction, replies to its requests and sends calculation results. In addition, it is used for publishing and testing all the algorithms, which are planned to be included in the algorithmic base on the server, using the embedded instruments. The server supports tools written in Python according to a special form after approval by the system administrator.
Python 2.7 with ArcPy library was used for geoprocessing services developing. ArcPy is a versatile package for efficient geodata analysis, conversion, management and mapping automation. An additional advantage of using ArcPy is that Python is a general-purpose programming language. It is interpreted and typed dynamically; besides, it is suitable for interactive work and rapid prototyping of small programs such as scripts. At the same time, it has enough functionality to create significant applications.
The client application was developed in JavaScript using HTML markup language and CSS language for appearance description. All the basic functions of a custom application were written using Dojo Toolkit and ArcGIS API for JavaScript 3.13 library. This powerful library makes it easy to work with maps in Web applications, as well as exchange data using REST API with servers based on ArcGIS for Server and ArcGIS Online services [ArcGIS for Developers: [website], URL: https://developers.arcgis.com/ javascript/jshelp/].
Dojo Toolkit is a framework for JavaScript. Its main features are the modularity and inheritance based on the use dojo/declare, which is not available in ordinary JavaScript.
The mapping application is developed using modern AMD (Asynchronous Module Definition) approach. AMD specifies a mechanism for defining modules and their dependencies to be loaded asynchronously. This approach is particularly well suited for browser environment where the modules are loaded simultaneously with the site content. Asynchronous module loading improves the speed of Web page loading in general. Additionally, AMD can be used for code partitioning into different files in the course of development of JavaScript applications [GitHub: [website], URL: https://github.com/amdjs/amdjs-api/wiki/AMD].
At the initialization stage, requests are transmitted to the predetermined server in order to get information about the published services. The server response returns in JSON format, which is converted into the object using Dojo means. Information on the published services is extracted from the object and again requests are sent to the server for a list of each service layers. Since the requests are asynchronous, the waiting time is minimal. Class dojo/promise/all is used to associate requests and responses of asynchronous type. Newly retrieved responses form an array of objects, which includes complete information on each layer.
The resulting array of objects which forms the basis of the hierarchy creation contains the following information about each service: name, URL address, array of layers of the service and tree levels.
Custom development Dijit CheckBox Tree version 0.9.4 for Dojo was used for implementation of layer management tool [Bit and or shift: [website], URL: http://www.thejekels. com/blog/featured/the-new-dijit-checkbox-tree/; Cbtree: [website], URL: http://thejekels.com/download/cbtree/]. A hierarchy is created basing on the previously obtained data array; event handler is connected, tree menu is generated and placed in a separate tab.
This particular feature of the developed tool provides dynamic update of the data list, which is available on the server, each time the application starts. Thus, every time it takes into account all added, modified or deleted data.
 |
| Figure 4 |
The results of layer management tool execution for geodatabase on Earth sciences (Figure 4), which are stored on the GIS server of GC RAS is sent to the screen and include the following:
Each geoprocessing service is implemented using Python language with ArcPy library. The program implies the following approach. First, the parameters are read using the function GetParameter. Next, the function GetLayer connects to the appropriate mapping service through httplib and urllib libraries using REST API. By means of JSON library it stores the response in the form of a JSON format file in a task folder and then converts it into a data layer.
The next step is the execution of the algorithm code selected by user from the algorithmic base.
At the end of the service implementation, the resulting resources are created on the server. Parameters of the layers generated as a result of the algorithm operation are assigned to output service values using the function SetParameter.
All temporary files are stored in a task folder on the server and removed with adjustable periodicity.
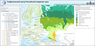 |
| Figure 5 |
The application interface is implemented using Dojo framework solutions. Application homepage is shown in Figure 5.
 |
| Figure 6 |
The application includes a map, a menu with the tabs on the left and a legend for added layers on the right. "Base map" tab contains a set of different base layers that can be changed at any time (Figure 6).
 |
| Figure 7 |
"Algorithms" tab contains a list of currently available algorithms (Figure 7). Published geoprocessing services are added to the application by the server administrator. Dynamic loading of services in the application is planned for the future.
The "Geodata Layers" tab contains layer management tools, described above.
 |
| Figure 8 |
The "Geoprocessing Results" tab displays the results of the algorithm application. It was built in the same manner as the layer management tool basing on Dijit CheckBox Tree. The legend is located on the right. It includes information on the layer and slider which controls the layer's transparency (Figure 8).
The developed visualization application has the following features:
 |
| Figure 9 |
By selecting an algorithm from the list and entering the required parameters, user creates a geoprocessing task. Figure 9 shows an example of the parameter input to the "Rodin-2" algorithm. The layer containing volcanoes in Russia was set as the input data.
User input is processed using regular expressions [Regular-Expressions.info: [website], URL: http://www.regular-exp ressions.info/], which makes the introduction of incorrect data impossible. By pressing the "Submit Job" button the task is sent to the server asynchronously, and upon successful completion the clustering result is automatically added to the map. The user is notified in case of an error.
 |
| Figure 10 |
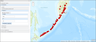
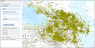
Clustering algorithms that are implemented in the application have been tested in the remote operation mode and have been applied to the data received from the GC RAS server via the Internet. The layer titled "Earthquake Epicenters in the Caucasus", shown in Figure 10, was used as the first set of real data for algorithms testing. The total number of elements in the selected layer was 6641. The objective was to define potentially earthquake-prone areas by recognition of dense regions.
 |
| Figure 11 |
Figure 11 shows the result of the DPS algorithm applied to the selected layer with the following parameters: $q = -3$ and $\beta = 0$.
 |
| Figure 12 |
 |
| Figure 13 |
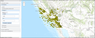
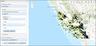
Figure 12 shows a second set of actual geodata, representing earthquake epicenters in California. The total number of the selected layer elements was 4098. Figure 13 shows the result of "Rodin-2" algorithm application to selected geodata set with the following parameters: $\alpha = 0.57$ and $P = -2.1$.
It is worth to mention that the described clustering algorithms, which have been added to the database so far, can only be applied to point data. Validation of input data type is automatically carried out at the beginning of each algorithm execution.
One of the important criteria for the application evaluation is its computational speed. Herein, it essentially means the speed of execution of a particular algorithm.
 |
| Table 1 |
Time of operation of each algorithm depends directly on the number of elements in the layer: the growing number of data in a layer increases the algorithm runtime. Table 1 shows the results of the computation time for the four clustering algorithms, which are included into the application, depending on the number of elements of a selected data layer. In this example, a computer, acting as a server, performing calculations had the following configuration: Intel(R) Core(TM) i5-2430 CPU 4 GHz, RAM 4 Gb, NVIDIA GeForce GT 540 M.
The developed software system is in some aspects unique and has no comparable counterparts. It provides a sophisticated study for the set of thematic layers on various categories, e.g. Earth sciences, with the use of data mining techniques. It provides data publication on the Internet and access for interested parties, in particular the scientific community. Published data become available worldwide without installing any additional software. It requires a Web browser and Internet access only.
The system is being constantly developed including extension of the geodatabase with new layers and filling the algorithmic base with new geoprocessing services representing data mining algorithms. It should be noted that the designed software system is a versatile tool. Besides geophysical research, it is also applicable in other thematic areas. For this purpose just another server should be set as a data source and the required geodata processing algorithms should be added in the application.
It is planned to expand the set of geoprocessing methods by adding algorithms for analyzing areal and linear objects, implement the feature of adding and processing custom user data from a client computer and introduce user authorization.
This GIS-oriented environment will enable focusing on the mathematical implementation of algorithms and results of their application.
Agayan, S. M., Sh. R. Bogoutdinov, M. N. Dobrovolsky (2011), About one algorithm for searching the dense regions and its geophysical applications, Reports of the 15th All-Russian conference "Mathematical methods for pattern recognition. MMPR", p. 543–546, Maks Press, Moscow (in Russian).
Agayan, S. M., Sh. R. Bogoutdinov, M. N. Dobrovolsky (2014), Discrete Perfect Sets and their application in cluster analysis, Cybernetics and Systems Analysis, 50, no. 2, p. 176–190.
Agayan, S. M., A. A. Soloviev (2004), Allocation of dense areas in metric spaces basing on crystallisation, System Research and Information Technologies, no. 2, p. 7–23 (in Russian).
Aivazyan, S. A. (1989), Applied Statistics: Classification and Dimensionality Reduction, 607 pp., Finance and Statistics, Moscow (in Russian).
Alekseev, V. A., E. M. Volodin, V. Ya. Galin, V. P. Dymnikov, V. N. Lykossov (1998), Modelling of the Present-Day Climate by the Atmospheric Models of INM RAS "DNM GCM" Preprint INM RAS., INM RAS, Moscow.
Berezko, A. E., A. A. Soloviev, A. D. Gvishiani, E. A. Jalkovski, R. I. Krasnoperov, S. A. Smagin, E. S. Bolotsky (2008), Intellectual geoinformation system "Earth sciences data for the territory of Russia", Engineering Ecology, no. 5, p. 32–40 (in Russian).
Beriozko, A., A. Lebedev, A. A. Soloviev, R. Krasnoperov, A. Rybkina (2011), Geoinformation system with algorithmic shell as a new tool for Earth sciences, Russ. J. Earth. Sci., 12, p. ES1001, doi:10.2205/2011ES000501.
Bogoutdinov, Sh., A. Gvishiani, S. Agayan, A. Soloviev, E. Kihn (2010), Recognition of Disturbances with Specified Morphology in Time Series. Part 1: Spikes on Magnetograms of the Worldwide INTERMAGNET Network, Izvestiya, Physics of the Solid Earth, 46, no. 11, p. 1004–1016.
Galin, V. Ya., E. M. Volodin, S. P. Smyshlyaev (2003), Atmospheric general circulation model of INM RAS with ozone dynamics, Russian Meteorology and Hydrology, no. 5, p. 7–15.
Gvishiani, A., S. Agayan, Sh. Bogoutdinov, A. Soloviev (2010), Discrete mathematical analysis and geological and geophysical applications, Vestnik KRAUNZ Earth Sci., 2, no. 16, p. 109–125 (in Russian).
Gvishiani, A., S. Agayan, Sh. Bogoutdinov, J. Zlotnicki, J. Bonnin (2008), Mathematical methods of geoinformatics. III. Fuzzy comparisons and recognition of anomalies in time series, Cybernetics and System Analysis, 44, no. 3, p. 309–323, doi:10.1007/s10559-008-9009-9.
Gvishiani, A. D., B. A. Dzeboev, S. M. Agayan (2013), A new approach to recognition of the strong earthquake-prone areas in the Caucasus, Izvestiya, Physics of the Solid Earth, 49, no. 6, p. 747–766, doi:10.1134/S1069351313060049.
Gvishiani, A., R. Lukianova, A. Soloviev, A. Khokhlov (2014), Survey of Geomagnetic Observations Made in the Northern Sector of Russia and New Methods for Analysing Them, Surveys in Geophysics, 35, no. 5, p. 1123–1154, doi:10.1007/s10712-014-9297-8.
Kaufmann, A. (1975), Introduction to the Theory of Fuzzy Subsets, Vol. 1, 416 pp., Academic Press, New York.
Lebedev, A. Yu., A. E. Beriozko (2009), Development of centralized catalog of geophysical data processing algorithms, Russ. J. Earth Sci., 11, p. RE2002, doi:10.2205/2009ES000399 (in Russian).
Okladnikov, I. G., A. G. Titov, T. M. Shul'gina, E. P. Gordov, Sh. R. Bogoutdinov, Yu. V. Martynova, S. P. Suschenko, A. V. Skvortsov (2013), A software complex for the analysis and visualization of monitoring and forecast of data on climate changes, Numerical Methods and Programming, 14, p. 123–131 (in Russian).
Shokin, Y. I., O. L. Zhizhimov, I. A. Pestunov, Y. N. Sinyavski, V. V. Smirnov (2007), Distributed informational-analytical system for searching, processing and analysis of spatial data, Computational Technologies, 12, no. 3, p. 108–115 (in Russian).
Sidorov, R. V., A. A. Soloviev, Sh. R. Bogoutdinov (2012), Application of the SP Algorithm to the INTERMAGNET Magnetograms of the Disturbed Geomagnetic Field, Izvestiya, Physics of the Solid Earth, 48, no. 5, p. 410–414.
Soloviev, A., S. Agayan, A. Gvishiani, Sh. Bogoutdinov, A. Chulliat (2012a), Recognition of Disturbances with Specified Morphology in Time Series: Part 2. Spikes on 1-s Magnetograms, Izvestiya, Physics of the Solid Earth, 48, no. 5, p. 395–409.
Soloviev, A. A., A. Chulliat, Sh. Bogoutdinov, A. D. Gvishiani, S. M. Agayan, A. Peltier, B. Heumez (2012b), Automated recognition of spikes in 1 Hz data recorded at the Easter Island magnetic observatory, Earth Planets Space, 64, no. 9, p. 743–752, doi:10.5047/eps.2012.03.004.
Soloviev, A., Sh. Bogoutdinov, S. Agayan, A. Gvishiani, E. Kihn (2009), Detection of hardware failures at INTERMAGNET observatories: application of artificial intelligence techniques to geomagnetic records study, Russ. J. Earth Sci., 11, p. ES2006, doi:10.2205/2009ES000387.
Soloviev, A., Sh. Bogoutdinov, A. Gvishiani, R. Kulchinskiy, J. Zlotnicki (2013), Mathematical Tools for Geomagnetic Data Monitoring and the INTERMAGNET Russian Segment, Data Science Journal, 12, p. WDS114–WDS119, doi:10.2481/dsj.WDS-019.
Soloviev, A. A., D. Yu. Shur, A. D. Gvishiani, V. O. Mikhailov, S. A. Tikhotskii (2005), Determination of the magnetic moment vector using cluster analysis of the local linear pseudoinversion of Delta T anomalies, Doklady Earth Sciences, 404, no. 7, p. 1068–1071.
Zelinskiy, N., N. Kleimenova, O. Kozyreva, S. Agayan, Sh. Bogoutdinov, A. Soloviev (2014), Algorithm for recognizing Pc3 geomagnetic pulsations in 1-s data from INTERMAGNET equatorial observatories, Izvestiya, Physics of the Solid Earth, 50, no. 2, p. 240–248.
Received 24 November 2015; accepted 1 December 2015; published 19 December 2015.


Citation: Nikolov B. P., J. I. Zharkikh, A. A. Soloviev, R. I. Krasnoperov, S. M. Agayan (2015), Integration of data mining methods for Earth science data analysis in GIS environment, Russ. J. Earth Sci., 15, ES4004, doi:10.2205/2015ES000559.
Copyright 2015 by the Geophysical Center RAS.