
RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 15, ES4003, doi:10.2205/2015ES000557, 2015
I. A. Panteleev1, V. A. Gavrilov2
1Institute of Continuous Media Mechanics, Ural Branch, Russian Academy of Sciences, Perm, Russia
2Institute of Volcanology and Seismology, Far Eastern Branch, Russian Academy of Sciences, Petropavlovsk-Kamchatskii, Russia
.We present the results of the work which continues our previous studies of the geoacoustic emission (GAE) responses to the weak impacts from the varying electromagnetic fields. In this paper, we analyze the probable influence exerted on the amplitude of GAE responses by the electrokinetic processes associated with the activation of filtration flows during the preparation of a tectonic earthquake of moderate magnitude. Based on the consolidation model of an earthquake source developed by I. P. Dobrovolsky, we suggest the model describing the generation of electrokinetic currents in response to the change in the volumetric strain in the source area of the future earthquake. Our model takes into account the physico-mechanical properties of the medium in the region of the measurement borehole and the physical properties and chemical composition of water in the measurement borehole itself. Using this model, we carry out the numerical experiments on simulating the evolution of the specific density of electrokinetic current in the time vicinity of a considered seismic event. The calculated variations in the specific density of electrokinetic current qualitatively coincide with the variations in the amplitude envelope of GAE responses.
The long multi-instrumental geophysical logging measurements conducted in the territory of the Petropavlovsk-Kamchatskii geodynamical testing area revealed a number of the nontrivial regularities reflecting the influence of the weak audio-frequency electromagnetic radiation (EMR) on the characteristics of geoacoustic emission (GAE) in the borehole environment. We note two key findings of these studies.
Primarily, it is the detection of the effect of GAE intensity modulation by the external audio-frequency EMR. This effect consists in the correlation between the variations in the root mean square (rms) GAE intensity and the changes in the amplitude of the varying external audio-frequency electric field which affects the geological medium in the region of the same borehole [Gavrilov, 2007; Gavrilov et al., 2006, 2011]. In particular, if the amplitude of the external electric field, either natural or man-made, has the distinct diurnal variations, then the rms GAE is modulated with a period of 24 h. The long regular measurements and the special in situ experiments show that with the geophones installed in the boreholes, the modulation effect of the external EMR on GAE intensity is detected even with the external electric fields as weak as $\sim 0.5$ mV/m [Gavrilov and Vlasov, 2011; Gavrilov et al., 2011].
Secondly, it was established that in the time vicinities of the earthquakes which exceed a certain threshold in terms of the parameter $S$ (see below), the modulation effect of the EM impacts on GAE intensity is more complicated. In this case, although the amplitude of the variations in the external EM impact is almost constant, the amplitude of the corresponding variations in GAE response may change quite rapidly and strongly [Gavrilov et al., 2006, 2008, 2013, 2014]. The quantity $S$ characterizes the degree of the probable influence on the stress strain state of the geological medium in the source zone of the future earthquake and is determined by the formula
\begin{eqnarray*} S=L/R_h \end{eqnarray*}where $L= 10^{0.44 M- 1.29}$ is the length of the earthquake source (in km) provided that the shape of the source can be approximated by an oval [Riznichenko, 1976]; $M$ is the magnitude of the event; and $R_h$ is the hypocentral distance in km. The earthquakes for which this effect is steadily observed are characterized by $S \geq 5\% $. In this case, the earthquakes can be preceded by both the degradation and growth in the amplitudes of GAE responses.
 |
| Figure 1 |
The example illustrating the manifestations of these effects is presented in Figure 1, which shows the simultaneous time series of the geoacoustic and electromagnetic measurements carried out in the G-1 borehole of the Petropavlovsk-Kamchatskii geodynamical testing area in October 2009.
The time dependences shown in this figure clearly illustrate the both effects. The modulating influence of the EM fields on GAE intensity manifests itself by the correlation between the diurnal variations in the EMR and GAE time series. The second effect is observed as the changes in the character of GAE in the time vicinity of the nearby earthquakes: the amplitude of the diurnal variations in EMR remains almost constant (Figure 1b), whereas the amplitude of the diurnal variations in GAE experiences rapid and strong changes in the time vicinity of the earthquake.
In [Gavrilov et al., 2013, 2014], we suggested the probable physical mechanisms of these effects, which are based on the analysis of the interplay between the filtration fields and the electric fields in the stressed medium. In particular, it was hypothesized that the GAE intensity in the time vicinities of relatively strong earthquakes could be affected by the electrokinetic processes associated with the fluid filtration in the zones controlled by the geophone. In the present work, we theoretically substantiate this hypothesis and construct the model describing the evolution of the electrokinetic current in the geological medium during the preparation of the single seismic event. An important feature of this model is that it maximally fully incorporates the existing data about the parameters of the geological medium in the zone of the G-1 borehole and the results of the combined multi-instrumental measurements carried out in this borehole by the Institute of volcanology and seismology of the Far Eastern Branch of the Russian Academy of Sciences in collaboration with the Kamchatka Branch of the Geophysical Survey of the Russian Academy of Sciences during the past 15 years.
The G-1 borehole is located within the limits of Petropavlovsk-Kamchatskii rather close to the different sources and consumers of the industrial electric power. In particular, at a distance of $\sim 500$ m from G-1 there is a high-voltage power line which determines the character of the EM impacts on the environment. The borehole has a depth of 2542 m and is cased throughout the entire length. In the depth intervals of 1710–1719, 1750–1754, 1790–1799, and 2415–2424 m, the casing pipe is perforated. The EM measurements in the borehole are conducted with the underground electric antenna [Gavrilov, 2013]. According to the long-term measurements, the EMR spectrum consistently shows a prominent enhancement (by about 5 dB) of the 150-Hz component during the dark time of the day, which determines the presence of the distinct diurnal variations in EMR after bandpass filtering with a central frequency of 150 Hz (Figure 1b). The calculated electric field intensity at a depth of 1000 m in the zone of the G-1 borehole is about 1.0 mV/m in the frequency band of $160 \pm 20$ Hz. The geoacoustic measurements in the G-1 borehole (Figure 1a) are conducted at a depth of 1012 m by the three-component geophone with A1612 piezoelectric sensors.
The physical mechanism accounting for the modulation effect exerted by the external audio-frequency electromagnetic field on GAE intensity is suggested in [Gavrilov et al., 2014]. According to the results obtained for fluid-saturated granular medium, the primary role in the physical mechanism of this effect belongs to the electrical double layers (EDL) which are formed on the interfaces between the solid and liquid phases. The fact that the viscous friction force between the mobile component of the liquid phase and the surface of the solid material depends on the amplitude of the external varying electric field is another important factor.
 |
| Figure 2 |
The electrical double layers, a necessary component of the interaction between the solid and liquid phases on their interface, are the spatially separated electric charges. At the same time, the EDL overall is electrically neutral. The present-day notions about the EDL structure are based on the Gouy-Chapman-Stern model [Salem, 2003], which is illustrated in the simplified form in Figure 2. EDL is composed of two parts. The inner part of EDL is a layer of the potential-determining ions (PDI). The external part of EDL is formed by the layer of counter-ions (CI).
The layer of the potential-determining ions is rather firmly anchored to the surface of the solid phase. It can be assumed that this layer is located in one plane with the surface of the solid phase. In the rocks, the solid phase typically has a negative charge and the fluid phase has a positive charge.
In contrast to the potential-determining ions which are localized on the surface of the solid phase, the counter-ions are diffusively distributed throughout the volume of the liquid phase. One part of counter-ions directly joins the interfacial surface due to chemical adsorption and electrostatic forces, where it forms a dense adsorption layer. The ions of the adsorption layer are rigidly connected to the interface of the phases. The thickness $\delta$ of the adsorption layer is approximately equal to the diameter of the hydrated ions composing it $(\sim 0.3 \div 0.4$ nm). The other part of the counter-ions is located in the diffuse layer which contains ion species of the both signs (with the predominance of the positive ones). The counter-ions overall form the bulk charge which is equal in the absolute value and opposite in the sign to the charge of the layer of the potential-determining ions.
The plane which separates the diffuse and adsorption layers is referred to as the Stern layer. The diffuse layer has an immobile and mobile parts separated by the sliding plane beyond which ions are able to move within the diffuse layer. The potential of the sliding plane, referred to as the electrokinetic or zeta potential ($\zeta$-potential), is the key parameter of EDL, which is directly related to the electrokinetic processes.
For the sliding plane located at a distance $s$ from the solid phase surface, the variations in the friction force caused by the external harmonic electromagnetic impact are described by the following formula [Gavrilov et al., 2014]:
\begin{equation} \tag*{(1)} \tau_s(t) \approx q_{s0} E_{s0} + E_m A \sin (\omega t - \psi) \end{equation}where the charge beyond the sliding plane $q_{s0}$ is unrelated to the external varying electric field; $E_{s0}$ is the intensity of the electrostatic field of EDL at a distance $s$ from the solid phase surface; $E_m$ is the amplitude of the external harmonic electric field, $\omega = 2 \pi f$ is the angular frequency of the signal; $A= \sqrt{q_{s0}^2 + [(\sigma S E_{s0})/(\omega)]^2}$ and quantity $\psi$ is determined from $ \cot \psi = (q_{s0} \omega)/(E_{s0} \sigma S)$.
From (1) it can be seen that under the external harmonic electromagnetic impact, the force of viscous friction between the mobile part of the liquid phase and the surface of the solid material on the EDL scale will fluctuate about the average value $q_{s0} E_{s0}$ with the frequency of the electromagnetic impact and phase delay $\psi$. The amplitude of the variations in the friction force will depend on the electric conductivity of the liquid fluid, amplitude of the electric field, and frequency of the external EMR.
In the borehole logging measurements, the recorded geoacoustic signal is formed by the superimposition of the emissions from a very large number of the individual GAE point sources which are acting simultaneously at the different points of the "noise" zone controlled by the geophone. The size estimates of the noise zone which determines the bulk ($\sim 90\% $) of the recorded GAE level indicate that in the case of the measurements in a deep borehole, this zone for the frequencies of 150–160 Hz is a sphere with a radius of at least a few hundred meters. On the scale of the noise zone, the cyclic decreases in the friction lead to the increase in the number of the acts of motion of the solid phase relative to the liquid fluid under the influence of the mechanical stresses acting in the geological environment due to the tectonic stresses, seismic wave impacts, tides, etc. In this case, as noted in [Gavrilov et al., 2014], the relationship between the variations in GAE intensity and the amplitude variations of the external electromagnetic field at low stresses has a stochastic character and is only detectable on rather long time intervals, commensurate with the periods of the variations in the EM field intensity.
The analysis of the different physical causes and factors which may affect the GAE intensity in the time vicinities of the earthquakes shows that when the strain rate in the geological medium significantly increases, the intensity of the geoacoustic processes is not exclusively determined by the external impacts but is also contributed by the filtration flows associated with the redistribution of the pore pressure [Gavrilov et al., 2013, 2014]. As a clear example of this influence, we cite the results of the in situ experiment conducted in the G-1 borehole in June 2014. In this experiment, about 50 liters of water were pumped out from the borehole on June 4.
 |
| Figure 3 |
 |
| Figure 4 |
Five days later, the water level in the borehole was artificially slightly raised. The geoacoustic signals were simultaneously recorded by two geophones installed at the depths of 270 and 1012 m. The intensity of the external EMR was monitored from the data of electromagnetic measurements with underground electric antenna [Gavrilov, 2013]. At the initial time instant after water pumping from the borehole, the trend component increased by $\sim 100\% $ compared to the average level during the previous 10 days (Figure 3). For the depth of 1012 m, the changes in the character of GAE were not so intense: the rms amplitude of the diurnal variations in GAE at a depth of 1012 m ($Y$-component, frequency channel 160 Hz) increased by $\sim 8\% $, whereas the maximal variations in the level of the trend component were at most 3% (Figure 4).
In this case, the growth in the amplitudes of the diurnal variations in GAE occurred with approximately a two-day time delay.
The data shown in Figure 4 suggest a high correlation between the trend components of the time series recorded in the different frequency channels for the same component of the geoacoustic signal. In this case, the growth in the level of the trend components in these time series corresponds to the instant of water pumping from the borehole, whereas the sharp drop of the level coincides with the time of the artificial water level heightening.
Generally, the results obtained in this experiment (Figure 3 and Figure 4) testify to the hydraulic connection of the G-1 borehole with the fracture space in the noise zones of the geophones installed at the depths of 270 and 1012 m. In this case, we may primarily conclude that the variations in the trend components of the GAE time series (Figure 3 and Figure 4) are due to the friction-related noise which results from the filtration flow in the pore-fracture near-borehole space. In other words, the variations in the trend components reflect the changes in the flow rate of the liquid fluid in the corresponding noise zone. In turn, the enhancement of the filtration processes resulted from the drop in the pore pressure of the rocks within the borehole environment due to the water pumping from the borehole. Secondly, as can be seen from the data presented in Figure 3 and Figure 4, the maximal growth in GAE amplitudes occurred on June 6 and 7, 2014 when the trend values of the GAE time series reached their maximum values. This result indicates a probable correlation between the amplitude variations of GAE responses and the enhancements of the electrokinetic processes during this time interval.
According to the contemporary physico-chemical notions [Dukhin, 1975; Fridrikhsberg, 1974], the electrokinetic phenomena include the electroosmosis, electrophoresis, and emergence of the streaming (filtration) potential and sedimentation potential. Primarily, the electrokinetic processes are the focus of interest for the problems dealing with monitoring the stress-strain state of the geological medium and short-term forecasting the earthquakes since these processes are characteristic of the time vicinities of the strong earthquakes [Dobrovolsky, 2009; Fitterman, 1979a; 1979b; Mizutani and Ishido, 1976].
With a sufficiently high strain rate in the fluid-saturated geological medium, significant variations arise in this medium in the electric field formed in response to the intensification of the filtration flows. If we assume equilibrium concentration of the oppositely charged ions in a selected rock volume (and, thus, neglecting the diffuse currents), we obtain the density of the total current associated with electrokinetic processes in the form of the sum of two terms [Fitterman, 1979b; Rastogi and Srivastava, 1993]:
$\;\;$
\begin{equation} \tag*{(2)} \boldsymbol{\mathrm{j}} = - \frac{\varepsilon_f \zeta}{F \mu_L} \nabla p (x,y,z,t) - \sigma\nabla\varphi(x,y,z,t) \end{equation}where $\varepsilon_f$ is the dielectric constant of a fluid, $\zeta$ is zeta potential determining the sliding plane in EDL, $\sigma = \sigma_f /F$ is the electric conductivity of the fluid-saturated rock, $\sigma_f$ is the electric conductivity of the fluid, $F$ is the geometric factor which depends on the geometry of the pore-fracture space in the rock, $\mu_L$ is the dynamic viscosity of the fluid, $\nabla p(x,y,z,t)$ is the gradient of the pore pressure, and $\nabla \varphi (x,y,z,t)$ is the gradient of the streaming potential. Factor $F$ is specified by the Archie-Dakhnov relationship: $F\approx \phi^{-m}$, where $\phi$ is rock porosity and $m$ is the degree of sedimentation of the rock.
The first term in the right-hand side of (2) is the density of the electrokinetic current, and the second term is the density of the oppositely directed conduction current caused by the emergence of the streaming potential. The electrokinetic effects result in the formation of a potential electric field with a complicated configuration which is imposed by the structure of the pore-fracture space of the medium. As is shown in [Gavrilov et al., 2014], the emergence and evolution of this field may entail the evolution of charges in the diffuse part of EDL, i.e. cause variations in the parameters of the electrostatic field of EDL. In accordance with (1) this should lead to the changes in the viscous friction between the mobile part of the liquid phase in EDL and the surface of the solid material [Gavrilov, 2014].
In turn, the variations in the viscous friction forces at the interfacial boundary can initiate the local repacking processes and amplify the shear defects on the different scale levels, which will excite elastic waves in the geological medium (i.e., induce the geoacoustic emission). The significant influence of the EDL parameters on the evolution of the defect structure of the rocks is experimentally demonstrated in the studies [Ishido and Nishizawa, 1984; Ishido and Mizutani, 1980]. In these works it was shown that the strength of the natural fluid-saturated dielectrics is affected by the EDL zeta potential at the interfacial boundaries and by the ionic force of the fluids.
Thus, in the time vicinity of the nascent nearby seismic event, we suggest the following chain of the processes implying the correlation between the amplitudes of GAE responses and the changes in the electrokinetic current density:
The key objective of the present work lies in promoting a better theoretical understanding of the evolution of electrokinetic current during the preparation of a tectonic earthquake and the mechanism of modulation of GAE parameters by electrokinetic effects. In the context of this research, based on the physical notions described above, we attempt to build a mathematical model describing the evolution of electrokinetic current during the preparation of a tectonic earthquake. The criterion of model adequacy to the processes taking place in the real geological medium is the agreement between the calculated variations in the total electrokinetic current density and the recorded variations in the amplitude envelope of GAE responses in the time vicinity of the nearby earthquake of moderate magnitude. For testing the model, we selected an isolated seismic event with the magnitude $M_l=5.2$, which occurred on October 8, 2009 at an epicentral distance $R_e=114$ km from the G-1 borehole at a depth of 10 km.
It is worth noting that as of now, the evolution of the electrokinetic current during the preparation of an earthquake is covered by relatively few theoretical works. As the most prominent investigations in this field, we cite the works [Dobrovolsky, 2009; Fitterman, 1979a, 1979b; Mizutani and Ishido, 1976, 1981]. In the present study, we describe the evolution of the electrokinetic current largely relying on the Dobrovolsky's approach, which is most suitable for solving the particular three-dimensional boundary problems. With the physical basis described above, the construction of the model for the evolution of the electrokinetic current during the preparation of a tectonic earthquake has three successive steps:
These calculations require specifying the model of the preparation of a tectonic earthquake. More than 30 such models have been developed to date. Among these, the avalanche-unstable fracture model [Myachkin, 1978] and the dilatancy-diffusion model [Scholz et al., 1973] are most popular and widely accepted. However, the qualitative character of these and the most other earthquake preparation models preclude calculation of the variations in the stress strain state of the rocks associated with the preparation of the future seismic event [Chelidze, 1987; Panteleev et al., 2012, 2013]. The consolidation model suggested by Dobrovolsky [Dobrovolsky, 1984, 2009, 2011] is an exception. At the same time, it is believed that the key points of this model have neither yet been validated by the laboratory experiments nor by the in situ field observations [Rogozhin et al., 2011].
In the present work, we used the consolidation model for calculating the 3D changes in the stress strain state of the rocks at the final stage of earthquake preparation. According to the Dobrovolsky's approach, the preparation of the source of the future earthquake occurs within a limited area whose elastic properties differ from the ambient rock. In other words, this area is a spatially limited heterogeneity in the elastic properties of the medium. The parameters and the size of this heterogeneity vary with time, and these variations are a direct cause of the emergence and evolution of the earthquake precursors of different nature. The preparation region of a future earthquake only differs from the hosting rocks by the shear modulus, and the shear modulus contrast between the heterogeneity and ambient rock can be both positive and negative. It is assumed that the heterogeneity before the earthquake can be approximated by the ellipsoid formed by the rotation of the fault ellipse around its major axis. In accordance with [Riznichenko, 1976], the major and minor axes of the fault ellipsoid are
\begin{equation} \tag*{(3)} L= 10^{0.44 M - 1.289} \; {\rm km}, \qquad l= 10^{0.401 M - 1.448} \; {\rm km} \end{equation}where $M$ is the magnitude of the event calculated from seismic moment. Considering the fact that the epicenter of the seismic event selected for the analysis was located at a distance of 100 km from the measurement borehole, the heterogeneity in the elastic properties of media was in this case treated as an equivalent sphere with a radius
\begin{eqnarray*} R= 10^{0.414 M - 1.696} \; {\rm km} \end{eqnarray*}The key point in the consolidation model of the earthquake preparation is the assumption that the preparation and occurrence of a seismic event are solely due to the changes in the physico-mechanical properties of the heterogeneity with time but not to the changes in the geometrical dimensions of this heterogeneity. Correspondingly, the onset of the stage of incipience of the precursory changes in the different physical fields corresponds to the beginning of the breakdown of the heterogeneity – the changes in its physico-mechanical properties, which tend to equalize the difference between the properties of the heterogeneity and ambient environment. In this case, the moment when the heterogeneity in the elastic properties completely disappears corresponds to the occurrence of the earthquake.
Within this approach, the perturbation in the stress strain state of the geological medium, which is caused by the emergence of heterogeneity in the elastic properties of the rock, is specified by the known solution of the Eshelby problem about a spherical heterogeneity in the elastic half- space [Eshelby, 1963]. For the further calculations, we use the formula for the volumetric strain of the elastic half-space with a spherical heterogeneity [Dobrovolsky, 2009]:
\begin{eqnarray*} \varepsilon = 2(1-2\nu) Gxy \Bigl( \Bigl[ \frac{1}{r_1^5} \Bigr] + \frac{3-4\nu}{r_2^5} - \frac{10 H (z+H)}{r_2^7} + \end{eqnarray*} \begin{eqnarray*} 2R^2 \Bigl( \frac{7(z+H)^2}{r_2^9} - \frac{1}{r_2^7} \Bigr) \Bigr) \end{eqnarray*}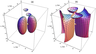 |
| Figure 5 |
where $G= \alpha \tau R^3/2 \pi \mu(1-\nu)$, $r_1= \sqrt{x^2 + y^2 + (z-H)^2}$, $r_2= \sqrt{x^2 + y^2 + (z+H)^2}$, $ \alpha$ is the relative change in the shear modulus within the heterogeneity, $\mu$ is the shear modulus of the medium, [Pa], $\nu$ is the Poisson ratio, $\tau$ is the tangential stress at infinity, [Pa], $H$ is the depth of the heterogeneity, [km], $R$ is the radius of the heterogeneity, [km], and the term in the square brackets only exists beyond the heterogeneity. Figure 5 shows the volumetric strain isosurfaces for the strains of $10^{-6}$ and $10^{-7}$ calculated for the selected seismic event with a magnitude of 5.2 and hypocentral depth of 10 km. These data demonstrate a complicated strain distribution whose structure is governed by the stress-free surface of the Earth.
The change in the volumetric strain in the region of the developing earthquake source leads to the redistribution of the fluid pore pressure and to the emergence of the filtration flows. To the first approximation, the evolution of the pore pressure in the geological medium can be calculated within the linear filtering theory. According to [Dobrovolsky, 2011], the equation for the changes in the pore pressure caused by the variation in the volumetric strain of the medium, has the following form:
\begin{equation} \tag*{(4)} \beta \frac{\partial p(x,y,z,t)}{\partial t} - \frac{k}{\mu_L m_0} \nabla^2 p (x,y,z,t)= - \gamma \frac{\partial \varepsilon(x,y,z,t)}{\partial t} \end{equation}where $p(x,y,z,t)$ is the excess (super-hydrostatic) pore pressure, [Pa], $\beta$ is the compressibility of the pore fluid, [Pa$^{-1}$], $k$ is the permeability of the rock, [m$^{-2}$], $\mu_L$ is the dynamic viscosity of the pore fluid, [Pa s], $m_0$ is the porosity of the rock, $\varepsilon(x,y,z,t)$ is the volumetric deformation of the rock caused by the emergence of heterogeneity, $\gamma$ is the coefficient of proportionality between the volumetric strains of the homogeneous medium and the pores.
This equation follows from the liquid phase mass balance equation and the momentum balance equation with elimination of the liquid phase velocity and with the assumption of a linear relationship between the volumetric strain of the initial medium and the volumetric strain of the pores. This relationship is described by the coefficient of proportionality $\gamma$. In the right-hand side of (4) there is the volumetric strain rate (the velocity of changes in the volumetric deformation) which is a governing parameter. Hypothesizing that the physico-chemical properties (viscosity and compressibility) of the fluid which fills the pore-fracture space of the rock in the region of the future earthquake do not vary with time, we may conclude that the character of evolution of the pore pressure during the preparation of the earthquake (and, consequently, the variations in the fluid saturation of the rock) are strongly affected by the porosity and the related permeability of the medium.
As was noted above, EDL – the spatially separated electric charges (Figure 2) – is the key attribute of the interaction between the solid and liquid phases at their interfacial boundary. The potential of the sliding plane (the $\zeta$ (zeta) potential) is the main EDL parameter which is directly related to the electrokinetic processes. The value of the zeta potential determines the intensity and direction of the currents associated with the emergence of the streaming potentials in a porous medium. A number of the previous theoretical works on electrokinetic precursors of the earthquakes [Fitterman, 1979a, 1979b] used the approximate estimates of the coefficient before the pore pressure gradient in (2) which includes the zeta potential. However, the results of the later experimental studies on measuring the zeta potential in the different media showed that it strongly depends on the parameters of the ion-conducting fluid (pH, ion composition, fluid salinity and temperature, etc.) [Revil et al., 1999; Tosha et al., 2003].
In the present study, we take into account this influence using the theoretical approach described in [Glover et al., 2012; Revil and Glover, 1997]. In this case, the zeta potential can be found as
\begin{eqnarray*} \zeta \approx \varphi_d \exp \Bigl( - \frac{\chi_\zeta}{\chi_d} \Bigr) \end{eqnarray*}where $\varphi_d$ is the potential of the Stern plane, $\chi_\zeta$ is the distance to the sliding plane, which is determined experimentally and which depends on the degree of mineralization of the fluid (fluid salinity) according to [Revil and Glover, 1997], we assumed $\chi_\zeta = 2.4 \times 10^{-10}$ m in our calculations); $\chi_d$ is the Debye length – the distance within which the environment is controlled by the electric field of an individual charge. The Debye length depends on the fluid temperature and salinity as
\begin{eqnarray*} \chi_d = \sqrt{ \frac{\varepsilon_f k_b T}{N_A e^2 C_f}} \end{eqnarray*}where $\varepsilon_f$ is the absolute (dielectric) permittivity of the fluid, [F m$^{-1}$]; $T$ is absolute temperature, [K]; $C_f$ is fluid salinity (concentration), [mole l$^{-1}$]; $k_b = 1.38 \times 10^{-23}$ is the Boltzmann constant, [J K$^{-1}$]; $N_A= 6.022\times 10^{23}$ is the Avogadro number, [mole$^{-1}$]; and $e = 1.602\times 10^{-19}$ is the elementary electric charge, [C]. The potential of the Stern plane is specified by the formula
\begin{eqnarray*} \varphi_d = \frac{2k_bT}{3e} \ln \left( \frac{\sqrt{ 810^3 \varepsilon_f k_b T N_A} {K_M}_e C_f}{2e \Gamma_s^0 K_{(-)}} \sqrt{C_f} \right) \end{eqnarray*}where $\varepsilon_f$ is the absolute permittivity of the fluid, [F m$^{-1}$], ${K_M}_e = 7.5$ is the constant of cation absorption of the fluid onto the surface of the solid phase; $\Gamma_s^0 \approx 10^{19}$ is the surface charge density, [m$^{-2}$]; and $K_{(-)}=7$ is the dissociation constant.
These relationships enable the the zeta potential to be calculated for a given fluid with the allowance for its temperature and salinity. In the present work, for finding the zeta potential, we use the data of the hydrochemical studies of the composition of water in the G-1 borehole presented in [Khatkevich and Ryabinin, 2006]. According to this work, water in the G-1 borehole is dominated by sodium chloride. Considering this, in our numerical calculations we assumed that the liquid fluid in the rocks of the G-1 borehole is a binary electrolyte. The average water salinity in the G-1 borehole in the time vicinity of the selected seismic event is 12.3 g/l with $pH = 9$.
The dielectric permittivity of the fluid is determined by the relationship $\varepsilon_f = \varepsilon_{c=0} + 3.79 \sqrt{C_f}$, where $\varepsilon_{c=0}$ is the permittivity of pure water, the electrical resistivity of the fluid with a given salinity is
$\rho_f = 0.5506$ Om m [Dobrynin et al., 2004], and the fluid dynamic viscosity is $5\times 10^{-4}$ Pa s. The temperature estimates for the water in the G-1 borehole at a depth of $\sim 1000$ m give $T=20\mbox{°}$ C. From the data obtained while drilling the G-1 borehole it is found that at a depth of 1000 m the borehole is surrounded by black and dark gray mudstones. Considering this, we may use the reference data for the physico-mechanical properties of the rock: the permeability is $10^{-13}$ m$^{-2}$, the degree of cementation of the rock is 2, and porosity is 2%.
The final problem of finding the electric field induced in the fluid-saturated geological medium by the variations in the pore pressure has the following form:
\begin{equation} \tag*{(5)} \left\{ \begin{array}{l} \boldsymbol{\mathrm j} = - \displaystyle{\frac{\varepsilon_f \zeta}{F \mu_L}} \nabla p (x,y,z,t) - \sigma\nabla\varphi(x,y,z,t) \mathrm{div} \boldsymbol{\mathrm j} = 0, \quad j_z|_{z=0} =0 \end{array} \right. \end{equation}where $\sigma = \sigma F \sigma_f$ is the electric conductivity of the fluid-saturated rock, [S m$^{-1}$].
On the Earth's surface, we assumed the no-flow boundary condition precluding the losses of the current into the atmosphere.
We reduce the problem (5) to the Laplace equation by combining the coefficients in (5):
\begin{eqnarray*} \boldsymbol{\mathrm j} = - \frac{\varepsilon_f \zeta}{F \mu_L} \nabla p (x,y,z,t) - \sigma\nabla\varphi(x,y,z,t) = \end{eqnarray*} \begin{equation} \tag*{(6)} - \sigma( \nabla\varphi (x,y,z,t) + C \nabla p (x,y,z,t)) \end{equation}where $C= \varepsilon_f \zeta/F\sigma \mu_L$ is the coefficient of the streaming potential. By substituting (6) into the Kirchhoff equation ${\mathrm{div}} \boldsymbol{\mathrm j}=0$, we obtain:
\begin{equation} \tag*{(7)} \left\{ \begin{array}{l} \mathrm{div} ( \sigma( \nabla\varphi (x,y,z,t) + C \nabla p (x,y,z,t)))=0 \left( \displaystyle{\frac{\partial\varphi}{\partial z} + C \frac{\partial p}{\partial z}} \right)_{z=0} =0 \end{array} \right. \end{equation}As a first approximation, we consider the case of a homogeneous isotropic geological medium. In this case, problem (7) is cast in the following form:
\begin{equation} \tag*{(8)} \left\{ \begin{array}{l} \nabla^2 (\varphi + Cp)=0 \left( \displaystyle{\frac{\partial(\varphi+ C_p)}{\partial z}} \right)_{z=0} =0 \end{array} \right. \end{equation}Problem (8) is the Laplace equation with the boundary condition on the surface, whose solution enables the analysis of the DC electric field in the homogeneous isotropic medium. The solution of this problem is trivial: $\varphi+ Cp =0$. From the solution it follows that with the arbitrary distribution of the excess pore pressure, a potential electric field arises such that the conduction current caused by this field is equal in magnitude and opposite in sign to the electrokinetic current. Due to the assumed boundary condition on the surface, only the vertical component of the electric field is nonzero, and its value is determined by the vertical component of the pore pressure gradient:
\begin{eqnarray*} E_z =- \frac{\partial \varphi}{\partial z}\Bigl|_{z=0} = C \frac{\partial p}{\partial z}\Bigl|_{z=0} \end{eqnarray*}where $E_z$ is the vertical component of the electric field, $\varphi$ is the streaming potential, and $C$ is the coefficient of the streaming potential.
In the time vicinity of the tectonic earthquake, the increase in the strain rate in the medium causes the intense fluid redistribution within a large spatial domain and the corresponding drastic change in the pore pressure gradient. In turn, the sharp change in the pore pressure gradient leads to the emergence of the uncompensated currents of electrokinetic nature, which interact with the charges of the diffuse part of EDL at the interfacial boundary between the mineral skeleton and the fluid. As has been noted above, this can eventually affect the GAE intensity.
We note that the hypothesis of homogeneous medium is very strong. In the real medium, with its complicated heterogeneous structure, also the both horizontal electric components are nonzero. However, this hypothesis significantly simplifies the problem and enables us to test the physical mechanism suggested for explaining the influence of the electrokinetic current on the amplitude of GAE response in a simple example – by direct numerical calculations.
The discussed statement of the problem about the evolution of electrokinetic current during the preparation of an isolated seismic event is a simplified model since the mechanical and physical properties of the fluid-saturated geological medium, which are known for a single spatial point (the geophone location point in the G-1 borehole), are expanded on all the points in the studied domain. This assumption is forced by the scarcity of the available data about the properties of the fluid-saturated rocks in a given region; however, it does not preclude establishing the qualitative picture of the studied process.
 |
| Figure 6 |
For conducting the numerical calculations, we should also assume a hypothesis concerning the position of the measurement borehole relative to the spherical elastic heterogeneity which emulates the developing seismic source. For the arbitrary seismic event, identifying the mechanism and orientation of the slip is a challenging problem which can only be solved after the occurrence of the event. The specificity of the solution of the Eshelby problem about a spherical heterogeneity in the elastic properties (with the origin of the coordinates at the center of the sphere) in the elastic half-space lies in the fact that the volumetric strain has the different signs in the different quadrants in Figure 6. In the first and third quadrants, the spherical heterogeneity causes positive volumetric strains (deformations of relative extension), whereas in the second and fourth quadrants it causes negative strains (deformations of relative compression). The sign of the volumetric strains determines the character of the changes in the pore pressure and, hence, the character of the changes in the pore pressure gradient. In the scope of the present work for the considered seismic event we assume that the measurement borehole is located in the first quadrant relative to the spherical heterogeneity.
We consider the limiting situation when the breakdown of the heterogeneity occurs instantaneously at the time moment $t=0$, which corresponds to the stepwise drop (to zero) of the parameter $\alpha$ (the relative change in the shear modulus in the heterogeneity). In this case, considering (4), the problem of finding the change in the pore pressure in the studied domain has the following form:
\begin{eqnarray*} \left\{ \begin{array}{c} \beta \displaystyle{\frac{\partial p (x,y,z,t)}{\partial t} - \frac{k}{\mu_L m_0}} \nabla^2 p (x,y,z,t)=0 p (x,y,z,0) = \gamma \varepsilon_{\max}, \quad p (x,y,0,t) =0 \end{array} \right. \end{eqnarray*} |
| Figure 7 |
Problem (4) is reduced to the homogeneous equation with the nonzero initial condition reflecting the deformation which is instantaneously experienced (acquired) by the medium during the breakdown of the heterogeneity, complemented by the boundary condition of the free liquid flow on the Earth's surface. The problem was solved numerically by the explicit finite-difference schemes. The solution of the general problem of the electrokinetic current evolution in the considered limiting case is illustrated in Figure 7. The solution is obtained for the spatial point corresponding to the position of the geophone in the measurement borehole G-1 at a given distance from the epicenter of the considered earthquake for the vertical components of the sought quantities.
The obtained time dependence of the electrokinetic current reflects the character of changes in the pore pressure in the region of the measurement borehole and has quite a transparent mechanical interpretation. Before the breakdown of the heterogeneity, the medium in the region of the measurement borehole is in the state of relative extension (compared to the situation when the heterogeneity is absent). At the time $t=0$, the heterogeneity instantly breaks up causing a momentary reduction in the volumetric strain in the rock up to the zero level, i.e. instantaneous compression if we assume the medium with heterogeneity as a reference configuration.
In turn, this process causes a sharp jump of the fluid pore pressure in the near-holw pore-fracture space due to the reduction of its volume. The magnitude of the jump in the pore pressure determines the initial intensity of the electrokinetic current in the obtained dependence at time $t=0$ (Figure 7). The fluid filtration processes cause the pore pressure to gradually flatten out, which, consequently, results in the reduction of the the electrokinetic current in the zone of the borehole. The intensity of the pore pressure decline is determined by the coefficient of piezoconductivity of the medium $k/(\beta\mu_L m_0)$ or, in the case of constant parameters of the fluid, by the porosity and permeability of the medium.
The numerical calculations of the electrokinetic current evolution in the limiting case demonstrated the close qualitative agreement with the geoacoustic measurements in the borehole, i.e. with the variations in the amplitude envelope of the GAE responses (Figure 7). At the same time, these calculations preclude identifying the stage of the earthquake preparation at which the electrokinetic current density starts to sharply change causing a drastic variation in GAE amplitudes.
 |
| Figure 8 |
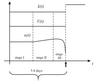
Considering this, in order to take into account the stage of the onset of the heterogeneity breakdown (which is likely to govern the emergence of the significant changes in the flow regime acting to enhance the electrokinetic phenomena), we should assume a number of the hypotheses about the character of changes in the parameters and properties of the heterogeneity. Figure 8 schematically illustrates the stages of the changes in the parameters of the heterogeneity which we assumed in our numerical experiment. The total duration of the stages shown in Figure 8 is 5.8 days.
Just as in the calculations for the limiting case, here we assumed that the volume of the heterogeneity remains unchanged with time up to the occurrence of the seismic event. This is the central point of the Dobrovolsky's model. The evolution of the parameter responsible for the relative change in the shear modulus within the heterogeneity has three characteristic stages (Figure 8). During the first stage, the parameter remains unchanged. This corresponds to the aseismic interval. At the second stage, the parameter slowly grows due to the action of the tectonic stresses or due to the triggering mechanisms of earthquake initiation. In fact, this reflects the enhancement of heterogeneity consolidation.
At the third stage, the parameter drops in an avalanche-like manner (following the power-law decay) to a certain level due to the breakdown of the heterogeneity and partial release of the accumulated elastic energy. The avalanche-like character of the earthquake source formation at the final stage of the preparation follows from the nonlinear collective evolution of the discontinuities in the geological medium, which is characteristic of all the deformed solids and media [Makarov, 2008; Panteleev and Naimark, 2014; Panteleev et al., 2012]. It is also assumed that the occurrence of the earthquake entails a jump-like growth in the permeability of the rocks located in the area of the heterogeneity [Scholz et al., 1973].
 |
| Figure 9 |
The data shown in Figure 9 allow us to compare the model density of electrokinetic current (Figure 9c), which is yielded by the numerical solution of the problem of electrokinetic current evolution during the preparation of the earthquake which occurred on October 8, 2009, with the results of the geoacoustic measurements in the G-1 borehole (Figure 9a and Figure 9b). These data demonstrate a close qualitative agreement between the calculated changes in the electrokinetic current and the variations in the envelope of the amplitude of GAE responses.
Considering the fact that the changes in the electrokinetic current density strongly depend on the intensity of filtration flows in the noise zone of the near-hole environment, let us give the mechanical interpretation to the observed regularities. At the first stage, when the parameter responsible for the relative change of the shear modulus within the heterogeneity remains unchanged, the pore pressure slightly decreases due to the diffusion of the fluid. As was previously noted, the intensity of this diffusion is controlled by the coefficient of piezoconductivity or, more specifically, permeability of the medium in the vicinity of the borehole. This influence is readily seen if we compare the rate of decrease of the electrokinetic current at the first and last (after the occurrence of the seismic event) stages. Figure 9 shows that the electrokinetic current decreases much faster after the earthquake. This result is determined by the third accepted hypothesis, i.e. the snowball-like growth in the permeability of the rock in the region of the heterogeneity due to the earthquake.
At the second stage (Figure 8), which is marked by the slow growth in the parameter $\alpha$, the relative extensional strains gradually build up and, consequently, the volume of the pore-fracture space in the medium also increases. In turn, this process leads to the drop in the pore pressure and relaxation of its gradient in the region of the measurement borehole, causing a relative decrease in the electrokinetic current density. The avalanche-like reduction in the parameter $\alpha$ (the third stage in Figure 8) leads to the qualitative transformation of the fluid regime: the strain rate of the rock drastically increases (the relative compressive strains sharply build up), the pore pressure grows in an avalanche-like manner due to the reduction of the volume of the pore-fracture space, and, as a result, the electrokinetic current sharply enhances. The time of occurrence of the seismic event is marked by the instantaneous termination of the changes in the parameter $\alpha$. Starting from this moment, the changes in the stress strain state of the medium are no longer determined by the evolution of the parameters of the elastic heterogeneity but, instead, they are purely governed by filtration flows in the hypocentral region of the event, which are associated with pore pressure redistribution.
It is worth noting that the calculated variations in the electrokinetic current density largely depend on the hypothesis determining the character of the time variations in the degree of heterogeneity of elastic properties in the source region of the future earthquake. Considering this, in our future studies we intend to focus on validating and refining the assumed hypotheses concerning the character of variations of the heterogeneity parameters during the preparation of the earthquake.
The studies described in the present work develop our previous investigations on establishing the physical mechanisms of the variations in the amplitudes of geoacoustic responses to the external EM impacts in the time vicinities of the strong nearby seismic events. The analysis of the long-term multi-instrumental geophysical measurements in the boreholes in the territory of the Petropavlovsk-Kamchatskii geodynamical site suggests that GAE intensity in the time vicinities of relatively strong seismic events is likely to be affected by the electrokinetic processes associated with fluid filtration in the zone controlled by the geophone.
For explaining the regularities in the variations of the recorded parameters, we constructed the model of the evolution of the electrokinetic current in the geological medium during the preparation of a single isolated seismic event. Our model relies on the consolidation model developed by I. P. Dobrovolsky and links the variations in the filtration flows in the geological medium to the emergence of the electrokinetic currents caused by the preparation of a tectonic earthquake and the breakdown of heterogeneity in the elastic properties in the infinite elastic half-space. The involvement of the hydrogeochemical data for water in the G-1 borehole together with the theoretical notions about the EDL structure and the dependence of zeta potential on temperature and water salinity enabled us to calculate the value of the zeta potential for the fluid in the pore-fracture space within the noise zone of the G-1 borehole.
Based on the constructed model, we have numerically modeled the evolution of the electrokinetic current density for two different scenarios of preparation of a tectonic earthquake. The first scenario is a limiting case when the accumulated elastic strain in the source area of the incipient earthquake, which is simulated by spherical heterogeneity in the elastic properties of the medium, is instantaneously transferred to the ambient environment at the time moment $t=0$. The second scenario takes into account the onset stage of the heterogeneity breakdown by assuming a number of the hypotheses about the character of the variations in the heterogeneity parameters. With the both scenarios, our calculations demonstrate the qualitative agreement between the character of evolution of the electrokinetic current density and the envelope of the GAE amplitudes. This enables us to conclude that the physical basis behind the constructed model is rather consistent.
Chelidze, T. L. (1987), Methods of Streaming Theory in Geomaterials Mechanics, 136 pp., Nauka, Moscow (in Russian).
Dobrovolsky, I. P. (1984), The Mechanics of Tectonic Earthquake Preparation, 189 pp., IFZ AN SSSR, Moscow (in Russian).
Dobrovolsky, I. P. (2009), Mathematical Theory of Preparation and Forecast of Tectonic Earthquakes, 240 pp., Fizmatlit, Moscow (in Russian).
Dobrovolsky, I. P. (2011), Perturbations of ground fluid flow at the preparation of tectonic earthquake, Geophys. Res., 12, no. 2, p. 33–47 (in Russian).
Dobrynin, V. M., B. Yu. Vendelshteyn, D. A. Kozhevnikov (2004), Petrophysics: Textbook for Universities, 368 pp., Oil and Gas, Moscow (in Russian).
Dukhin, S. S. (1975), Electroconductivity and Electrokinetic Properties of Dispersive Systems, 346 pp., Naukova Dumka, Kiev (in Russian).
Eshelbi, J. (1963), Continual Theory of Dislocations, 248 pp., Inost. Lit., Moscow (in Russian).
Fitterman, D. V. (1979a), Calculations of the self-potential anomalies near vertical contacts, J. Geophys. Res., 44, no. 2, p. 195–205, doi:10.1190/1.1440961.
Fitterman, D. V. (1979b), Theory of electrokinetic-magnetic anomalies in a faulted half-space, J. Geophys. Res., 84, no. B11, p. 6031–6040, doi:10.1029/JB084iB11p06031.
Fridrikhsberg, D. A. (1974), The Course of Colloidal Chemistry, 352 pp., Khimiya, Leningrad (in Russian).
Gavrilov, V. A. (2007), Physical causes of diurnal variations in the geoacoustic emission level, Doklady Earth Science, 414, no. 1, p. 638–641, doi:10.1134/S1028334X07040320.
Gavrilov, V. A. (2013), About method of continuous monitoring of rocks electrical resistivity, Journal of Seismic Instruments, 49, no. 3, p. 25–38 (in Russian).
Gavrilov, V. A., Yu. A. Vlasov (2011), The effect of modulation of geoacoustic emission level by super-low frequency electromagnetic radiation from measurements on different boreholes of Petropavlovsk-Kamchatsky geodynamic polygon, Problems of complex geophysical monitoring the Russian Far East, Materials of III scientific and technological conference, 09–15 October 2011, p. 207–211, RAS, Petropavlovsk-Kamchatsky (in Russian).
Gavrilov, V. A., Yu. V. Morozova, A. V. Storcheus (2006), Geoacoustic emission level variations in deep borehole G-1 (Kamchatka) and their relation to seismic activity, J. Volcanology and Seismology, 1, p. 52–67 (in Russian).
Gavrilov, V., L. Bogomolov, Yu. V. Morozova, A. Storcheus (2008), Variations in geoacoustic emissions in a deep borehole and its correlation with seismicity, Ann. Geophys., 51, no. 5/6, p. 737–753.
Gavrilov, V. A., L. Bogomolov, A. S. Zakupin (2011), Comparison of the geoacoustic measurements in boreholes with the data of laboratory and in-situ experiments on electromagnetic excitation of rocks, Izvestiya, Phys. Solid Earth, 47, no. 11, p. 1009–1019, doi:10.1134/S1069351311100041.
Gavrilov, V. A., et al. (2013), Modulating impact of electromagnetic radiation on geoacoustic emission of rocks, Russ. J. Earth Sci., 13, p. ES1002, doi:10.2205/2013ES000527.
Gavrilov, V. A., I. A. Panteleev, G. V. Ryabinin (2014), The physical basis of the effects caused by electromagnetic forcing in the intensity of geoacoustic processes, Izvestiya, Phys. Solid Earth, 50, no. 1, p. 87–101, doi:10.1134/S1069351314010042.
Glover, P. W. J., E. Walker, M. D. Jackson (2012), Streaming-potential coefficient of reservoir rock: A theoretical mode l, Geophysics, 77, no. 2, p. D17–D43, doi:10.1190/geo2011-0364.1.
Ishido, T., H. Mizutani (1980), Relationship between fracture strength of rocks and $\zeta$-potential, Tectonophysics, 67, p. 13–23, doi:10.1016/0040-1951(80)90161-4.
Ishido, T., O. Nishizawa (1984), Effects of zeta potential on microcrack growth in rock under relatively low uniaxial compression, J. Geophys. Res., 89, no. B6, p. 4153–4159, doi:10.1029/JB089iB06p04153.
Khatkevich, Yu. M., G. V. Ryabinin (2006), Hydrogeochemical studies in Kamchatka in connection with the search for earthquake precursors, J. Volcanol. Seism., 4, p. 34–42 (in Russian).
Makarov, P. V. (2008), Mathematical theory of evolution of loaded solids and media, Physical Mesomechanics, 11, no. 5–6, p. 213–227, doi:10.1016/j.physme.2008.11.002.
Mizutani, H., T. Ishido (1976), A new interpretation of magnetic field variation associated with the Matsushiro earthquakes, J. Geomagn. Geoelectr., 28, p. 179–188, doi:10.5636/jgg.28.179.
Mizutani, H., T. Ishido (1981), Experimental and theoretical basis of electrokinetic phenomena in rock-water systems and its applications to geophysics, J. Geophys. Res., 86, no. B3, p. 1763–1775, doi:10.1029/JB086iB03p01763.
Myachkin, V. I. (1978), Processes of Earthquake Preparation, 232 pp., Nauka, Moscow (in Russian).
Panteleev, I. A., O. B. Naimark (2014), Current trends in the mechanics of tectonic earthquakes, Vestnik Permskogo Nauchnogo Tsentra UB RAS, no. 3, p. 44–62 (in Russian).
Panteleev, I. A., O. A. Plekhov, O. B. Naimark (2012), Nonlinear Dynamics of the Blow-Up Structures in the Ensembles of Defects as a Mechanism of Formation of Earthquake Sources, Izvestiya, Phys. Solid Earth, 48, no. 6, p. 504–515, doi:10.1134/S1069351312060055.
Panteleev, I. A., O. A. Plekhov, O. B. Naimark (2013), Model of geomedia containing defects: Collective effects of defects evolution during formation of potential earthquake foci, Geodynamics & Tectonophysics, 1, p. 37–51, doi:10.5800/GT-2013-4-1-0090.
Rastogi, R. P., R. C. Srivastava (1993), Nonequilibrium Thermodynamics of Electrokinetic Phenomena, Chem. Rev., 93, no. 6, p. 1945–1987, doi:10.1021/cr00022a001.
Revil, A., P. W. J. Glover (1997), Theory of ionic surface electrical conduction in porous media, Physical Review B: Condensed Matter and Materials Physics, 55, p. 1757–1773, doi:10.1103/PhysRevB.55.1757.
Revil, A., P. A. Pezard, P. W. J. Glover (1999), Streaming potential in porous media 1. Theory of the zeta potential, J. Geophys. Res., 104, no. B9, p. 20,021–20,031, doi:10.1029/1999JB900089.
Riznichenko, Yu. V. (1976), Sizes of Crustal Earthquake Focus and Seismic Moment, Investigation for Physics of Earthquake Source, 9–26 pp., Nauka, Moscow (in Russian).
Rogozhin, E. A., et al. (2011), Potential Seismic Foci and Seismological Precursors of Earthquakes – Basis of Real Seismic Forecast, 368 pp., Svetoch Plyus, Moscow (in Russian).
Salem, R. R. (2003), Theory of Double Layer, 104 pp., Fizmatlit, Moscow (in Russian).
Scholz, C. H., L. R. Sykes, Y. P. Aggarawal (1973), Earthquake prediction: A physical basis, Science, 181, p. 803–810, doi:10.1126/science.181.4102.803.
Tosha, T., N. Matsushima, T. Ishido (2003), Zeta potential measured for a intact granite sample at temperatures to 200° C, Geophys. Res. Lett., 30, no. 6, p. 1295, doi:10.1029/2002GL016608.
Received 3 November 2015; accepted 17 November 2015; published 4 December 2015.


Citation: Panteleev I. A., V. A. Gavrilov (2015), Implications of electrokinetic processes for the intensity of geoacoustic emission in the time vicinity of a tectonic earthquake: A theoretical study, Russ. J. Earth Sci., 15, ES4003, doi:10.2205/2015ES000557.
Copyright 2015 by the Geophysical Center RAS.