
RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 15, ES4002, doi:10.2205/2015ES000556, 2015
O. I. Parphenuk
Institute of Physics of the Earth, Russian Academy of Sciences, Moscow, Russia
.The investigation of collision structures is conducted based on the complex model of the thermal and mechanical evolution of overthrusting process for the rheologically layered lithosphere, which includes brittle upper crust and the lower crust and lithospheric upper mantle with different effective viscosity values. Finite element models with Lagrangian approach were used for the problem simulation. Horizontal shortening leads to the upper crust overthrusting along the fault zone, additional loading to the lower layers which is redistributed in the process of erosion of the uplift. These processes are compensated by ductile flow at the level of the lower crust and the upper mantle. The results of modeling of collision belts evolution during and after the convergence process have been compared for main governing parameters: shortening velocity (strain rate), viscosity contrast, erosion rate and dip angle of thrusting. The calculations with different erosion rates (0.25–5 mm/yr) show that this process has a weak effect on the postcollisional uplift evolution, which is governed mainly by the viscosity values of the lower crust and lithosphere upper mantle and initial geometry of the structure. But denudation results in surface exposure of metamorphic sequences, typical for thrust faults.
The structure, geometry and evolution of collisional orogens remain a complicated problem of geophysics. In the past years, a great number of important contributions have been made to the understanding of collisional dynamics. Some of them deal with Andean-type collision, which is a geodynamical process of subduction, where a lower and denser plate underthrusts a gravitationally stable continent. Alpine-type collision is characterized by convergence of two continental buoyantly similar plates whose dynamical evolution is governed by the process of overthrusting.
In recent years numerical modeling has been used widely to investigate convergence between continental plates [e.g. Beaumont et al., 2001; Burg and Gerya, 2005; Burov et al., 2001; England, Thompson, 1984; Willett et al., 1993] and significant progress has been achieved in understanding of orogenic processes. The numerical studies of collision are based on models with different aspects and details of collisional orogens, which also includes constraints from the thermal structure observed in mountain chains by thermobarometric studies [e.g. Faccenda et al., 2008; Jammes, Huismans, 2012].
Common features of collisional overthrusting tectonics include high temperature metamorphic rocks exposed at the surface due to erosion, widespread granite magmatism, gravity and magnetic anomalies, often crustal thickening under the orogen uplift, complex zone of seismic reflections and high velocities, which characterize layering and stratified structure.
 |
| Figure 1 |
Precambrian continental shields such as the Anabar, Baltic and Canadian, are the structurally stable areas for at least the last 1.6 Ga. Deeply eroded structures of the shields formed in the process of multistage tectonic evolution including horizontal shortening and collision expose at the surface middle to the lower crustal rocks uplifted along the faults from the depths 20–40 km. These exposures exhibit asymmetric patterns of metamorphic grade and age across the faults, distinctive Bouguer anomalies reflecting dipping basement structure and often anomalously deep crustal roots. Thermal and deformation structures formed by the crustal thickening and shortening determine to a considerable extent the further evolution of a tectonic unit, subjected to compression. Extension in orogenic zones, defined as horizontal stretching of a lithosphere, that has undergone thickening and shortening, involving perturbations of the lithosphere thermal regime, may be a respond to the increase of vertical stress due to the surface elevation and buoyant roots. There are several examples of compressional belts that did not experience lithospheric-scale post-orogenic extension [Mareschal, 1994; Percival, 1990]. A crustal root is preserved beneath the Appalachians, some parts of the Grenville front, under the Kapuskasing structural zone in the Superior Province of the Canadian Shield, the Limpopo belt of Southern Africa, collision belts in the Anabar Shield (Figure 1).
High temperature metamorphism and widespread granite magmatism are common features of many ancient continental collision structures. Deeply eroded areas of the Archean and Proterozoic continental shields formed in the process of tectonic evolution including horizontal shortening and collision expose at the surface middle to the lower crust rocks. This phenomenon seems to be valid also for active collision zones. The massive layer of granite melt approximately of 10 km thickness is observed at 10–15 km depth by seismic methods in the resent orogens such as the Himalayas [Rosen, Fedorovsky, 2001]. The Paleozoic Variscan orogen in Europe is characterized by large volumes of felsic granites intruded during HT-LP metamorphism and exposed in deeply eroded parts of the Variscan belt (South Bohemian Batholith) [Gerdes et al., 2000].
Fundamental features of collision zones reflect the effect of the main tectonic event – horizontal shortening in compression setting, collision of two continental plates accompanied by the thickening of the crust and the surface uplift. Extensive development of horizontal and oblique motions of crustal plates and blocks leads to the disturbances in the thermal regime, heat flow, the surface and Moho topography. The main petrologic mark of such collision is granite melt generated at different depth's levels and exposed at the surface as a result of the uplift and denudation.
Thermal-kinematic model of continental collision calculates pressure, velocity and temperature fields and includes horizontal shortening, brittle overthrusting in the upper crust compensated by the lower crust viscous flow and erosion of the thickened crust. Finite-element 2-D modeling is used to examine the uplift history with surface denudation, post-orogenic stage, the thermal and kinematic conditions for high-temperature metamorphism and the depth and timing of crustal melting in the case of rheologically layered lithosphere.
\ttt\caption{Basic Parameters Values Used in the Mechanical (1) and Thermal (2) Problems of Evolution Modeling}
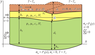 |
| Figure 2 |
We are presenting here a model of continental convergence of relatively light plates which leads to upthrusting of brittle upper crust and results in ductile flow in the lower crust and lithospheric upper mantle. The coupled thermal-mechanical model is developed based on mechanical model for overthrusting zones [Parphenuk, 2014; Parphenuk, Mareschal, 1998]. Figure 2 shows the geometry of a two-dimensional model of the lithosphere and boundary conditions used to simulate ductile flow in the lower crust (yellow) and the upper mantle (green) as a result of shortening, loading, and erosion in overthrusting region, as well as thermal evolution in the area including the upper crust (brown). We assume that the rigid upper crust subjected to horizontal shortening and overthrusting is broken by vertical faults into separate blocks weakly connected one with another. Such a rigid but flexible layer can be displaced without contraction and extension. The geometry and uplift algorithm are presented in [Parphenuk, 2014]. The numerical modeling is thus not concerned with the brittle deformation in the upper crust: the overthrusting and erosion are not included directly in mechanical calculations but are introduced as boundary conditions. In the right upper part of the model, the effect of additional loading due to overthrusting is introduced in the boundary condition by the vertical stress equal to the lithostatic pressure of the overlying material. We assume, that the lower crust and the lithospheric mantle have constant density and behave like linear (Newtonian) fluids with constant effective viscosity $(\rho_1<\rho_2$ and $\mu_1 < \mu_2)$.
Inertial forces are negligible compared with viscous forces (the process is very slow and the rock viscosities are very high, i.e., the Reynolds number is negligibly small). The equations of momentum and mass conservation for an incompressible Newtonian fluid then describe the ductile flow in the lower crust and lithospheric upper mantle (Figure 2):
\begin{equation} \tag*{(1)} \left\{ \begin{array}{c} \mu_i\nabla^2 {\mathbf u} - \nabla P - \rho_i {\mathbf g} = 0 \nabla^2 {\mathbf u}=0 \end{array} \right. \end{equation}where $\mathbf g$ is the acceleration due to gravity, $P$ is the pressure, $\rho$ is the density, ${\mathbf u}= (u,v)$ is the velocity, $\mu$ is the effective kinematic viscosity. The subscript denotes the material properties of the layer ($i = 1$ corresponds to the lower crust and $i = 2$ to the lithospheric mantle).
Shortening is simulated by a moving vertical left boundary and no-slip condition under the moving brittle upper crust. The horizontal velocity on the upper boundary is the same as that of the moving upper crust left of the fault and it vanishes right of the fault. The normal stress varies horizontally because of the lateral variations in mass of upper crustal material due to the loading redistribution by erosion and sedimentation. The upper crust overlying the ductile region acts as a passive load, and the underlying part of the lithosphere is deflected under the loading; the implicit assumption is that the flexural rigidity of the upper crust is neglected in these calculations. A lithostatic equilibrium condition is assumed at the right boundary. The viscosity of the underlying asthenosphere is considered much lower than that of the lithospheric mantle and a lithostatic equilibrium condition is assumed at the lower boundary
\begin{eqnarray*} \rho_1 gd_1 + \rho_2 gd_2+ \rho_3 gd_3 = \mathrm{const} \end{eqnarray*}The condition of local isostasy compensation at the deeper level than given boundary in asthenosphere with the same density as the lithospheric mantle is approximated by the condition that the normal stress is equal to the lithostatic pressure at that depth without loading:
\begin{eqnarray*} P_3(x) = \rho_3 gh_3 + \rho_1 gh_1+ \rho_2 g (h_2+h_m) \end{eqnarray*}The effective viscosity of the thickened lower crust remains in the range $10^{20}- 10^{22}$ Pa s and it is higher in the underlying upper mantle with values in the range $10^{21}- 10^{23}$ Pa s. The lower boundary of the lithosphere will be deflected because of both shortening and loading.
The Navier-Stokes equations, the incompressibility condition, and the boundary conditions were solved by the finite-element method with Lagrange approach. In these calculations, the nonuniform grid is deformed with time and the nodes thus follow the real deformation history. Some details of the numerical method used are described in [Parphenuk et al., 1994] and numerical method itself is based on the FEM algorithms developed in [Reddy, 1984]. Calculations of velocity and temperature fields are based on crustal thickening by overthrusting with dip angle of faulting of 15–30° and shortening rate in the range of 0.5–4 cm/yr. Total amount of horizontal shortening is 70–100 km. We assume that erosion and concurrent sedimentation begin after an additional crustal portion of a substantial thickness is exposed.
The equation of energy conservation is solved for the case of Lagrange coordinates with material time derivative [Turcotte, Shubert, 1985]:
\begin{equation} \tag*{(2)} c_i\rho_i \frac{DT}{Dt} = \lambda_i\nabla^2 T + H_i \end{equation} |
| Table 1 |
where $c$ is specific heat, $\rho$ is density, $\lambda$ is the thermal conductivity, and $H$ is the heat generation rate. The model of thermal evolution thus consists of three layers: 20 km brittle upper crust ($i = 3$ – upper brown layer), 20 km ductile lower crust ($i = 1$, yellow) and 80 km lithospheric mantle ($i = 2$, green) with different thermal, kinematic and rheological parameters (Figure 2). Table 1 lists the values of the basic parameters used for solution of mechanical (1) and thermal (2) problems.
The main attention was focused on the study of thermal conditions, viscosity contrast, duration and rate of crustal shortening and erosion that could produce significant lateral variations in crustal thickness and topography uplift, gravity anomalies, progressively increasing paleopressures along the exposed upthrusted layer and some other features of collision zones.
The results of mechanical modeling of evolution of collision belts during and soon after the convergence process have been compared for main governing parameters: the shortening rate (strain rate), viscosity contrast, erosion rate and dip angle of thrusting. The mechanisms of erosion and sedimentation are poorly known, so we assumed a simplified approach to this problem: the high-elevated regions of the overthrust zone are eroded and the material removed is deposited in the lower elevation parts; erosion with fixed or decreasing rate was imposed after some time interval following the beginning of collision. The shortening rate in the range 0.5–4.0 cm/yr and the initial dip angle of the fault 15–30° were used depending on the studied structure.
 |
| Figure 3 |
 |
| Figure 4 |
The numerical study of collision orogen developed as a result of horizontal shortening of the lithosphere and overthrusting of the upper crust confirm that this thermal-mechanical model with ductile flow in the lower crust can be feasible mechanism, explaining many features of Precambrian collision belts. Under the assumptions and approximations of the model the calculations show that for geologically reasonable strain rates $10^{-15} - 10^{ -14}$ s$^{-1}$ combination of 70–100 km shortening, loading due to overthrusting, erosion and sedimentation lead to the formation of deep crustal roots (by about 10–20 km over a region 100–200 km wide), surface uplift and surface metamorphic sequences, typical for thrust faults. When the process of convergence is terminated at some stage, the evolution continues with redistribution of the surface load by erosion and sedimentation. The change of tectonic stage is simulated by the modification of boundary conditions. The area subjected to convergence is adjusting to the loading redistribution and the rate of adjustment is determined by erosion rate and viscosity contrast. Further erosion reduces the depth of crustal root and contracted region is slowly extending (Figure 3 and Figure 4).
 |
| Figure 5 |
The rocks exposed at the surface will show paleopressures resulted from upthrusting and erosion. In the model including 70 km of shortening with velocity 1 cm/yr, dip angle of faulting $\alpha = 20\mbox{°}$ and viscosity values $5\times 10^{21}$ Pa s in the lower crust and $5\times 10^{21}$ Pa s in the upper mantle, metamorphic sequences correspond to erosion level increasing monotonously from about 0.03 km to about 14 km across the thrust fault (Figure 5).
 |
| Figure 6 |
The dip angle affects mainly the width and thickness of the root: higher angles produce a narrow and deep root (Figure 6).
Geological structure of collision zones formed in the processes of shortening, overthrusting and erosion at the level of the upper crust, which are compensated by ductile flow in the lower crust and upper mantle, plays a major role in their thermal evolution. The zones of melting which produce collisional granitoids essentially result from the geometry and topography due to thrusting [Jaupart, Provost, 1985]. The amount of crustal thickening and the tectonic stresses required to sustain shortening and overthrusting constrain the range of viscosity values to $10^{21} - 10^{22}$ Pa s in the lower crust and $10^{21} - 10^{22}$ Pa s in the upper mantle.
The calculations of thermal evolution show the possibility of the partial melting and granite melt generation subjected to the main thermal parameters of the model – the initial temperature distribution, radiogenic heat production and thermal conductivity. The temperature increase can be fairly significant (up to 250° C) at depths level of 10–30 km confirming the idea of crustal origin of the continental collision granites. The partial melting (wet granite solidus) appears in the thickened crust in the vicinity of thrust fault and widens in the direction of thrusting and to the lesser depths. Maximum temperature increase along the fault zone is 300° C [Parphenuk, 2012].
2-D collision model confirms the observation of a wide range of $P - T$ conditions over short distances in metamorphic belts [Chamberlain, Karabinos, 1987]. As a result of upward motion along the fault, the additional loading redistribution in the course of erosion, and the viscous compensation at the level of the lower crust, $P - T$ histories will be completely different for the points along the thrust fault. For example, for the convergence and erosion rates of 0.5 cm/yr and 0.025 cm/yr, respectively, maximum erosion level of $\sim$11 km of uplifted crust is reached at 45 Ma after the onset of collision (at postcollisional stage). The material will be transported from a depth of 20 km to a depth of about 5 km while the rocks that were initially located at a depth of 3.5 km will experience a rather complicated $P-T$ evolution. At the postcollisional stage (after 20 Ma of shortening) the compressional regime is changed by extension with very low velocities.
The numerical study of collision orogens developed as a result of horizontal shortening of the lithosphere and overthrusting of the upper crust confirm that this thermal-mechanical model with ductile flow in the lower crust can be feasible mechanism, explaining many features of collision belts. Under the assumptions and approximations of the model the calculations show that for geologically reasonable strain rates $10^{-15} - 10^{-14}$ s$^{-1}$ combination of 70–100 km shortening, loading due to overthrusting, erosion and sedimentation lead to the formation of deep crustal roots (by about 10–20 km over a region 100–200 km wide), surface uplift and surface metamorphic sequences, typical for thrust faults. When the process of convergence is terminated at some stage, the evolution of gravitationally unstable area continues with redistribution of the surface load by erosion and sedimentation. The area subjected to convergence is adjusting to the loading redistribution and the rate of adjustment is determined by erosion rate and viscosity contrast.
The calculations with different erosion rates (0.25–5 mm/yr) show interesting result: this parameter has a weak effect on the postcollisional uplift value, which is governed mainly by the viscosity values of the lower crust and lithospheric upper mantle. For example, the one order increase of the lower crust viscosity from $5\times 10^{21}$ Pa s to $5\times 10^{22}$ Pa s results in decreasing velocity of postcollisional uplift from 1 mm/yr to 0.15 mm/yr. But denudation is the main process in deep crustal rocks exposure, which is observed in wide range of $P - T$ conditions over short distances in metamorphic belts. It also leads to the lower depth of partial melting zone which is observed at $10-15$ km depth by seismic methods in young orogens.
The possibility of preservation of crustal roots depends on the number of parameters, the most important of which are the initial dip angle of fault, the rate of shortening and erosion rate, the thermal conditions and viscosity values and contrast between the lower crust and upper mantle. Relatively narrow range of temperatures exists compatible with a viscosity low enough for formation of a crustal root by ductile deformation in the lower crust and high enough in the mantle to preserve the crustal root, avoiding lithospheric scale extension. The rheology and thermal conditions that lead to the formation and preservation of crustal roots have been discussed in [Parphenuk, Mareschal, 1998; Parphenuk et al., 1994].
The following set of parameters is critical to initiate crustal melting and granite formation: initial temperature distribution with heat flow density value about 60 mW/m$^2$, relatively high radiogenic heat production, slow crustal thickening (0.5–1 cm/yr for 10–20 Ma) and slow exhumation. Some of results of the thermal modeling [Parphenuk, 2005, 2012] confirm other model estimates [England, Thompson, 1984; Gerdes et al., 2000] and will be discussed in details in the next paper.
Beaumont, C., R. A. Jamieson, M. H. Nguyen, B. Lee (2001), Himalayan tectonics explained by extrusion of a low-viscosity crustal channel coupled to focused surface denudation, Nature, 414, p. 738–742, doi:10.1038/414738a.
Burg, J. P., T. V. Gerya (2005), The role of viscous heating in Barrovian metamorphism of collisional orogens: thermomechanical models and application to the Lepontine Dome in the Central Alps, J. Metamorp. Geol., 23, p. 75–95, doi:10.1111/j.1525-1314.2005.00563.x.
Burov, E., L. Jolivet, L. Le Pourhiet, A. Poliakov (2001), A thermomechanical model of exhumation of high pressure (HP) and ultrahigh pressure (UHP) metamorphic rocks in Alpine-type collision belts, Tectonophysics, 342, p. 113–136, doi:10.1016/S0040-1951(01)00158-5.
Chamberlain, C. P., P. Karabinos (1987), Influence of deformation on pressure–temperature paths of metamorphism, Geology, 15, p. 42–44, doi:10.1130/0091-7613(1987)15<42:IODOPP>2.0.CO;2.
England, P., A. B. Thompson (1984), Pressure-temperature-time paths of regional metamorphism. Part I: Heat transfer during the evolution of regions of thickened continental crust, J. Petrology, 25, p. 894–928, doi:10.1093/petrology/25.4.894.
Faccenda, M., T. V. Gerya, S. Chakraborty (2008), Styles of post-subduction collisional orogeny: Influence of convergence velocity, crustal rheology and radiogenic heat production, Lithos, 103, p. 257–287, doi:10.1016/j.lithos.2007.09.009.
Gerdes, A., G. Worner, A. Henk (2000), Post-collisional granite generation and HT-LP metamorphism by radiogenic heating: the Variscan South Bohemian Batholith, J. Geol. Soc, London, 157, p. 577–587, doi:10.1144/jgs.157.3.577.
Jammes, S., R. S. Huismans (2012), Structural styles of mountain building: Controls of lithospheric rheologic stratification and extensional inheritance, J. Geophys. Res., 117, p. B10, doi:10.1029/2012JB009376.
Jaupart, C., A. Provost (1985), Heat focusing, granite genesis and inverted metamorphic gradients in continental collision zones, Earth Planet. Sci. Lett., 73, p. 385–397, doi:10.1016/0012-821X(85)90086-X.
Mareschal, J.-C. (1994), Thermal regime and post-orogenic extension in collision belts, Tectonophysics, 238, p. 471–484, doi:10.1016/0040-1951(94)90069-8.
Parphenuk, O. I. (2005), Thermal regime of collisional overthrust structures, Izvestiya, Physics of the Solid Earth, 41, no. 3, p. 238–240.
Parphenuk, O. I. (2012), Study of thermal conditions of granite melt formation in collision areas (based on numerical simulation), Monitoring. Science and Technology, 3, no. 12, p. 11–20 (in Russian).
Parphenuk, O. I. (2014), Analysis of the collisional uplifts erosion influence on the overthrusted structures and the process of deep crustal rocks exhumation (numerical modeling), Bulletin of Kamchatka regional association Educational-Scientific Center, Earth Sciences, no. 1(23), p. 107–120 (in Russian).
Parphenuk, O. I., V. Dechoux, J.-C. Mareschal (1994), Finite-element models of evolution for the Kapuskasing structural zone, Can. J. Earth Sci., 31, p. 1227–1234, doi:10.1139/e94-108.
Parphenuk, O. I., J.-C. Mareschal (1998), Numerical modeling of the thermomechanical evolution of the Kapuskasing structural zone, Superior Province, Canadian Shield, Izvestiya, Physics of the Solid Earth, 34, no. 10, p. 805–814.
Percival, J. A. (1990), A field guide through the Kapuskasing uplift, a cross section through the Archean Superior Province, Exposed Cross-Sections of the Continental Crust, NATO ASI Ser., 317, p. 227–283.
Reddy, J. N. (1984), An Introduction to the Finite-Element Method, 459 pp., McGrow-Hill, New York.
Rozen, O. M. (1995), Metamorphic effects of tectonic movements at the low crustal level: Proterozoic collision zones and terranes of the Anabar Shield, Geotectonics, 29, p. 91–101.
Rosen, O. M., V. S. Fedorovsky (2001), Collisional Granitoids and the Earth Crust Layering, 188 pp., Nauchnyi Mir, Moscow (in Russian).
Turcotte, D., J. Shubert (1985), Geodynamics, Vol. I, 376 pp., Mir, Moscow (translated to Russian).
Willett, S., C. Beaumont, P. Fullsack (1993), Mechanical model for the tectonics of doubly vergent compressional orogens, Geology, 21, p. 371–374, doi:10.1130/0091-7613(1993)021<0371:MMFTTO>2.3.CO;2.
Received 5 November 2015; accepted 12 November 2015; published 27 November 2015.


Citation: Parphenuk O. I. (2015), Uplifts formation features in continental collision structures (evolution modeling), Russ. J. Earth Sci., 15, ES4002, doi:10.2205/2015ES000556.
Copyright 2015 by the Geophysical Center RAS.