RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 14, ES3002, doi:10.2205/2014ES000543, 2014
S. M. Agayan, Sh. R. Bogoutdinov, M. N. Dobrovolsky, A. I. Kagan
Geophysical Center of Russian Academy of Science, Moscow, Russia
.This article continues the series of papers by the authors on the new universal DMA-smoothing of time series, originally intended for the analysis of geophysical time series obtained in the framework of discrete mathematical analysis (DMA), developed by GC RAS. We formulated the general concept of weighted DMA-smoothing, constructed and analyzed one of its variants.
Time series are the most effective way to represent dynamic data, the results of various kinds of monitoring (physical, geophysical, environmental et al.). Smoothing of time series is one of the most powerful tools to study them, because the smoothed time series often are simpler, more amenable to simple analysis and serve as an effective approximation of the original time series.
To date, the most known methods of smoothing are regression analysis, finite element method and splines, Fourier and wavelet smoothing and their generalizations based on expansions in orthogonal systems of functions and time-frequency analysis.
The proposed method expands the list of a new type of smoothing, able to operate successfully in the analysis of geophysical time series. In the article it was applied to real data from the Borok geomagnetic observatory of the INTERMAGNET network.
Let $\mathrm {TS}[a,b]$ be a space of time series on a discrete segment $[a,b]$ with nodes $t_{i} =a+(i-1)h$, $i=1, \ldots ,n$, $h= (b-a)/(n-1)$. The elements of $\mathrm {TS}[a,b]$ are denoted by $x$, $y$, $z$, $\dots$. If $z\in \mathrm {TS}[a,b]$, then $z_{i} =z(t_{i} )$ and the correspondence $z\sim (z_{i} )|_{1}^{n} $ turns $\mathrm {TS}[a,b]$ into $n$-dimensional Euklidian space $R^{n} =R^{n} (z_{1} ,\ldots ,z_{n} )$.
We considered the task of constructing the smoothing $\mathrm{Sm} \, y\mathop{=}\limits^\mathrm {def} x\in \mathrm {TS}[a,b]$ for the given time series $y\in \mathrm {TS}[a,b]$. Its solution is a consistent formalization of the following conjunction:
\begin{equation} \tag*{(1)} \begin{array}{c} \textrm{"}x - \textrm{smoothing } y \textrm{"} \equiv ( x - \textrm{approximation } y)\, \wedge \, (x - \textrm{smoothed time series}) \end{array} \end{equation}Let us denote by $z$ a variable series in $\mathrm {TS}[a,b]$. The approximation in (1) is formalized by the quadratic residual functional $\mathrm {Sc}(z|y)=||z-y||^{2} $, and the smoothness – by the non-negative quadratic form $\mathrm {CG}(z)$, which we call the smoothness residual. It is based on a variant of the discrete continuity. The residual $\mathrm {CG}(z)$ is a measure of the deviation from this property for the time series $z$ on the interval $[a,b]$. The less are the values $\mathrm {Sc}(z|y)$ and $\mathrm {CG}(z)$, the more reason we have to consider $z$ the smoothing $y$. Consequently, we need a meaningful simultaneous minimization of the functionals $\mathrm {Sc}(z|y)$ and $\mathrm {CG}(z)$. To do this, we considered their nontrivial convex combination
\begin{eqnarray*} \mathrm{Sm}_{\lambda } (z|y)=\lambda \mathrm {CG}(z)+(1-\lambda ) \mathrm {Sc}(z|y), \lambda \in (0,1) \end{eqnarray*}and a search of the smoothing $x=\mathrm{Sm}\, y$ for $y$ is reduced to a minimization on $\mathrm {TS}[a,b]$ at a suitable $\lambda \in (0,1)$ of the functional $\mathrm{Sm}_{\lambda } (z|y)$, i.e. to the solution of the $n$-dimensional linear system
\begin{eqnarray*} x=\mathrm{Sm}_{\lambda } y \, \Leftrightarrow \, \mathrm{Grad}\, \mathrm{Sm}_{\lambda } (x|y)=0 \end{eqnarray*}Thus we suggest the whole family $\{ \mathrm{Sm}_{\lambda } y,\; \lambda \in (0,1)\} $ as the smoothing $\mathrm{Sm}\, y$. Let us find the gradient $\mathrm{Grad}\, \mathrm{Sm}_{\lambda } (x|y)$ in its clear form. For that first we introduce the non-negative on $\mathrm{TS}[a,b]$ operator $\mathrm{G}$, which generates the gravitational smoothness residual $\mathrm{CG}(z)=(\mathrm{G}\, z,z)$ and then we transform $\mathrm{Sm}_{\lambda } (z|y)$:
\begin{eqnarray*} \mathrm{Sm}_{\lambda } (z|y)=\lambda (\mathrm{G}\, z,z)+(1-\lambda )||z-y||^{2} = \end{eqnarray*} \begin{eqnarray*} \lambda (\mathrm{G}\, z,z)+(1-\lambda )(z-y,z-y)= \end{eqnarray*} \begin{eqnarray*} \lambda (\mathrm{G}\, z,z)+(1\!- \!\lambda )(z,z)-2(1 \!- \!\lambda )(z,y)+(1 \!- \!\lambda )||y||^{2} = \end{eqnarray*} \begin{eqnarray*} ((\lambda \mathrm{G}+(1-\lambda )\mathrm{E})z,z)-2(1-\lambda )(z,y)+(1-\lambda )||y||^{2} \end{eqnarray*}Hence $\mathrm{E}$ is a unit operator on $\mathrm{TS}[a,b]$. Consequently, the minimization $\mathrm{Sm}_{\lambda } (z|y)$ is equal to the functional minimization
\begin{eqnarray*} \widetilde{\mathrm{Sm}}_{\lambda } (z|y)=\frac{1}{2} ((\lambda \mathrm{G}+(1-\lambda )\mathrm{E})z,z)-((1-\lambda )z,y) \end{eqnarray*}For it the gradient in the point $z$ is expressed through $\mathrm{G}$ like this [Pshenichny and Danilin, 1975]:
\begin{eqnarray*} \mathrm{Grad}\, \widetilde{\mathrm{Sm}}_{\lambda } (z|y)=(\lambda \mathrm{G}+(1-\lambda )\mathrm{E})z-(1-\lambda )y \end{eqnarray*}Thus,
\begin{eqnarray*} x=\mathrm{Sm}_{\lambda } y \, \Leftrightarrow \, (\lambda \mathrm{G}+(1-\lambda )\mathrm{E})x=(1-\lambda )y \end{eqnarray*}If $\lambda \in (0,1)$, then the operator $\lambda \mathrm{G}+(1-\lambda )\mathrm{E}$ is positive on $\mathrm{TS}[a,b]$, and therefore reversible. Consequently, the smoothing $x=\mathrm{Sm}_{\lambda } y$ always exists, is uniquely defined for any $y\in \mathrm{TS}[a,b]$ and represents the result of applying the operator $(\lambda \mathrm{G}+(1-\lambda )\mathrm{E})^{-1} $, therefore
\begin{eqnarray*} \mathrm{Sm}_{\lambda } =(1-\lambda )(\lambda \mathrm{G}+(1-\lambda )\mathrm{E})^{-1} \end{eqnarray*}Let us consider an important variant of the residual $\mathrm{CG}(z)$.
Let us briefly (according to the module [Agayan et al., 2010; Gvishiani et al., 2011]) consequently, from top to bottom recall the construction of the main, but not the only one residual of the discrete smoothness $\mathrm{CG}(z)$: the gravitational smoothness residual $\mathrm{CG}r(z)$:
\begin{eqnarray*} \mathrm{CG}r(z)=\sum_{s=0}^{n-1} \omega_{s} \mathrm{CG}r^{s} (z) \end{eqnarray*}where $\omega_{s} $ is the non-negative weights (parameters of smoothness). The residual $\mathrm{CG}r(z)$ was generated by the operator of gravitational smoothness $\mathrm{Gr}$:
\begin{eqnarray*} \mathrm{CG}r(z)=(\mathrm{Gr}\, z,z), \, \mathrm{Gr}=\sum _{s=0}^{n-1} \omega _{s} \mathrm{Gr}^{s} \end{eqnarray*}where
\begin{eqnarray*} \mathrm{Gr}^{s} = \mathrm{D}^{s^{*}} \mathrm{Gr}[a,b^{s}]\mathrm{D}^s \end{eqnarray*}and $\mathrm{D}^{s} $ is the $s$-dimensional discrete differentiation operator: if $z$ is the time series on the interval $[a,b]$, then its $s$-dimensional derivative $z^{s} =\mathrm{D}^{s} z$ is time series on the interval $[a,b^{s} ]$, $b^{s} = b-sh$ and in each node $t_{i} \in [a,b^{s} ]$
\begin{eqnarray*} z^{s} (t_{i} )=\frac{\sum _{l=0}^{s} (-1)^{s-l} C_{s}^{l} z_{i+l} }{h^{s} } \end{eqnarray*}
The operator $\mathrm{Gr}[a,b^{s} ]$ is called the operator of gravitation continuity residual on the interval $[a,b^{s} ]$ and is defined by the proximity measure $\delta _{t_ {i}} ^{s} (t_{j} )$ in accordance with the following formula
\begin{eqnarray*} \mathrm{Gr}[a,b^{s}]=(\mathrm{A}(\delta ^{s}) -\mathrm{E})^{*} (\mathrm{A}(\delta ^{s}) -\mathrm{E}) \end{eqnarray*} \begin{eqnarray*} \mathrm{A}(\delta ^{s})=(a_{ij}^{s} ) \end{eqnarray*} \begin{eqnarray*} \displaystyle{a_{ij}^{s} =\frac{\delta _{i} ^{s} (j)}{\sum_{j=1} ^{n-s} (\delta _{i} ^{s} (j))}} \end{eqnarray*}One of the following constructions was used as the proximity measure:
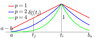
\begin{eqnarray*} \begin{array}{c} \delta_{i}^{s} (j) =\delta _{t_{i} } ^{s}(t_{j} )= \displaystyle{\left(1-\frac{|t_{j} -t_{i} |}{\max (|t_{i} -a|,|t_{i} -b_{s} |)+h}\right)^{p}} \end{array} \end{eqnarray*} |
| Figure 1 |
as shown in Figure 1, or
\begin{eqnarray*} \delta_i^s(j)= \delta_i^{s,r}(j)= \delta_{t_i}^{s,r}(t_j)= \left\{ \begin{array}{cc} \displaystyle{\left(1-\frac{|t_j-t_i|}{r} \right)^{p}} & \mathrm{if} \quad |t_j-t_i| \lt r, \\ \\ 0 & \mathrm{if} \quad |t_j-t_i| \ge r. \end{array} \right. \end{eqnarray*}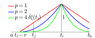 |
| Figure 2 |
for a certain $r < b_s -a$, as shown in Figure 2
Thus there are three free parameters of gravitational smoothing: the coupling multiplier $\lambda \in [0,1]$, the system $w$ of non-negative weights $w_{s}, \, s=0,\dots,n-1$ and the system $\delta$ of proximity measures $\delta ^{s}, s=0,\dots,n-1$, which depends on the internal parameter $p \ge 0$.
These parameters give the gravitational smoothing greater flexibility and expressiveness. The study allows some qualitative conclusions about their relationship to be made:
 |
| Figure 3 |
 |
| Figure 4 |
 |
| Figure 5 |
 |
| Figure 6 |
Let us assume that each node $t_{i}$ in the interval $[a,b]$ has its non-trivial weight $v_{i} \ge 0$. Let us denote by $\boldsymbol{\mathrm V}$ their total population $\boldsymbol{\mathrm V}=\{v_{i}|_{1} ^{n}\}$. This raises the question of the impact of $\boldsymbol{\mathrm V}$ on the DMA-smoothing, which is the subject of this paragraph. The functional
\begin{eqnarray*} \mathrm{Sm}_{\lambda } (x|y) = \lambda \mathrm{CG}(x) + (1- \lambda )\mathrm{Sc}(x|y) \end{eqnarray*}is responsible for the smoothing, so the impact $\boldsymbol{\mathrm V}$ occurs separately: through the smoothness residual $\mathrm{CG}(x)$, the scanning functional $\mathrm{Sc}(x|y)$ and the connecting multiplier $\lambda $.
In the future we shall also denote by $\boldsymbol{\mathrm V}$ the diagonal operator with weights $v_{i}$. Further, the smoothing elements, into which the weights $\boldsymbol{\mathrm V}$ have (or have not) penetrated, will be respectively denoted by $\mathrm{CG}_{\mathrm V} (x)$, $\mathrm{Sc}_{\mathrm V} (x|y)$, $\lambda _{\mathrm V}$ ($\mathrm{CG} (x)$, $\mathrm{Sc} (x|y)$, $\lambda $). Relationships between the smoothing $\mathrm{Sm}$ and the weights $\boldsymbol{\mathrm V}$ in a general case can develop according to one of the following eight scenarios:
\begin{eqnarray*} \mathrm{Sm}_{\lambda } (x|y) = \lambda \mathrm{CG}(x) + (1- \lambda )\mathrm{Sc}(x|y) \end{eqnarray*} \begin{eqnarray*} \mathrm{VSm}_{\lambda } (x|y) = \lambda \mathrm{CG}(x) + (1- \lambda )\mathrm{Sc}_{\mathrm V}(x|y) \end{eqnarray*} \begin{eqnarray*} \mathrm{SmV}_{\lambda } (x|y) = \lambda \mathrm{CG}_{\mathrm V} (x) + (1- \lambda )\mathrm{Sc}(x|y) \end{eqnarray*} \begin{eqnarray*} \mathrm{VSmV}_{\lambda } (x|y) = \lambda \mathrm{CG}_{\mathrm V} (x) + (1- \lambda )\mathrm{Sc}_{\mathrm V} (x|y) \end{eqnarray*} \begin{equation} \tag*{(2)} \mathrm{Sm}_{\lambda_{\mathrm V}} (x|y) = \lambda_{\mathrm V} \mathrm{CG}(x) + (1- \lambda_{\mathrm V} )\mathrm{Sc}(x|y) \end{equation} \begin{eqnarray*} \mathrm{VSm}_{\lambda _{\mathrm V} } (x|y) = \lambda _{\mathrm V} \mathrm{CG}(x) + (1- \lambda_{\mathrm V} )\mathrm{Sc}_{\mathrm V}(x|y) \end{eqnarray*} \begin{eqnarray*} \mathrm{SmV}_{\lambda _{\mathrm V} } (x|y) = \lambda _{\mathrm V} \mathrm{CG}_{\mathrm V} (x) + (1- \lambda _{\mathrm V} )\mathrm{Sc}(x|y) \end{eqnarray*} \begin{eqnarray*} \mathrm{VSmV}_{\lambda_{\mathrm V} } (x|y) = \lambda_{\mathrm V} \mathrm{CG}_{\mathrm V} (x) + (1- \lambda_{\mathrm V} )\mathrm{Sc}_{\mathrm V} (x|y) \end{eqnarray*}The interest in the structures (2) is explained by the following circumstances: in general stochastic setting smoothing of time series can be considered as a possible option of ideal course of the process, which is described by the given time series. If the disturbances of process in time are expressed by weights, the weighted smoothing gives an idea of the impact of these disturbances on the process.
The simplest is the impact of $\boldsymbol{\mathrm V}$ on the scanning $\mathrm{Sc}(x|y)$: it is natural to assume that
\begin{eqnarray*} \mathrm{Sc}_{V} (x|y) = \sum_{i=1} ^{n} v_{i} (x_{i} - y_{i} )^{2} \end{eqnarray*}If the weights $v_i{}$ are positive, then the operator $\boldsymbol{\mathrm V}$ is reversible and the smoothing $x=\mathrm{Sm} y$ (2) looks like this
\begin{eqnarray*} \mathrm{Sm}_{\lambda } \,y = (1 - \lambda )(\lambda \mathrm{G} + (1- \lambda )\mathrm{E})^{-1} y \end{eqnarray*} \begin{eqnarray*} \mathrm{VSm}_{\lambda } \,y = (1 - \lambda )(\lambda \mathrm{G} + (1- \lambda )\mathrm{E})^{-1} \boldsymbol{\mathrm V}y \end{eqnarray*} \begin{eqnarray*} \mathrm{SmV}_{\lambda } \,y = (1 - \lambda )(\lambda \mathrm{G}_{\mathrm V} + (1- \lambda )\mathrm{E})^{-1} y \end{eqnarray*} \begin{eqnarray*} \mathrm{VSmV}_{\lambda } \,y = (1 - \lambda )(\lambda \mathrm{G}_{\mathrm V} + (1- \lambda )\mathrm{E})^{-1} \boldsymbol{\mathrm V}y \end{eqnarray*} \begin{equation} \tag*{(3)} \mathrm{Sm}_{\lambda_{\mathrm V}} \,y = (1 - \lambda_{\mathrm V} )(\lambda_{\mathrm V} \mathrm{G} + (1- \lambda_{\mathrm V} )\mathrm{E})^{-1} y \end{equation} \begin{eqnarray*} \mathrm{VSm}_{\lambda_{\mathrm V} } \,y = (1 - \lambda_{\mathrm V} )(\lambda_{\mathrm V} \mathrm{G} + (1- \lambda_{\mathrm V} )\mathrm{E})^{-1} \boldsymbol{\mathrm V}y \end{eqnarray*} \begin{eqnarray*} \mathrm{SmV}_{\lambda_{\mathrm V} } \,y = (1 - \lambda_{\mathrm V} )(\lambda_{\mathrm V} \mathrm{G}_{\mathrm V} + (1- \lambda_{\mathrm V} )\mathrm{E})^{-1} y \end{eqnarray*} \begin{eqnarray*} \mathrm{VSmV}_{\lambda_{\mathrm V} } \,y = (1 - \lambda_{\mathrm V} )(\lambda_{\mathrm V} \mathrm{G}_{\mathrm V} + (1- \lambda_{\mathrm V} )\mathrm{E})^{-1} \boldsymbol{\mathrm V}y \end{eqnarray*}To summarize, there are seven non-trivial scenarios of varying degrees of penetration depth of the weights $\boldsymbol{\mathrm V}$ of nodes in the DMA-smoothing $\mathrm{Sm}$. The simplest is the second scenario $\mathrm{VSm}_{\lambda }$ ((2) and (3)) in which the weights of nodes penetrate the scanning only.
We conclude this work with the analysis of such smoothing in the gravitational case.
 |
| Figure 7 |
 |
| Figure 9 |
In all the smoothings in Figure 7–Figure 9 the nodes of the main record $y$ were supposed to be equal, having a unit weight. Let us break this equality three times by giving
In each case at the same parameters $\lambda$, $w$ and $p$ we constructed the smoothings $\mathrm{Sm}_{\lambda } \,y$ and $\mathrm{VSm}_{\lambda } \,y$. In Figure 7–Figure 9 the smoothing $\mathrm{Sm}_{\lambda } \,y$ is shown in blue and outside the intervals [18:30–18:50] and [19:50–20:10] is concealed by the smoothing $\mathrm{VSm}_{\lambda } \,y$, shown in red. Our study has shown that the situation in Figure 7–Figure 9 typical for the correlation of $\mathrm{Sm}_{\lambda } \,y$ and $\mathrm{VSm}_{\lambda } \,y$ and allows the following conclusion to be made: under the same conditions $\lambda$, $w$, $p$ the smoothings $\mathrm{Sm}_{\lambda } \,y$ and $\mathrm{VSm}_{\lambda } \,y$ have the same smoothness, at that the construction $\mathrm{VSm}_{\lambda } \,y$ is clearly dependent on the weights $\mathrm{V}$: the higher is the weight $v_i$ in the node $t_i$, the more carefully the smoothing $\mathrm{VSm}_{\lambda } \,y$ scans the record $y$ in the vicinity $t_i$.
Agayan, S. M., A. D. Gvishiani, Sh. R. Bogoutdinov, A. I. Kagan (2010), Smoothing of time series by methods of discrete mathematical analysis, Russian Journal of Earth Sciences, 11, RE40001, doi:10.2205/2009ES000436.
Gvishiani, A. D., S. M. Agayan, Sh. R. Bogoutdinov, A. I. Kagan (2011), Gravitational smoothing of time series, Institute of Mathematics and Mechanics of the Ural Branch of the Russian Academy of Sciences, 17, 2, 62–70.
Pshenichny, B. N., Yu. M. Danilin (1975), Numerical Methods in Extremal Tasks, Nauka, Moscow, 319.
Received 12 December 2014; accepted 14 December 2014; published 30 December 2014.


Citation: Agayan S. M., Sh. R. Bogoutdinov, M. N. Dobrovolsky, A. I. Kagan (2014), Weighted gravitational time series smoothing, Russ. J. Earth Sci., 14, ES3002, doi:10.2205/2014ES000543.
Copyright 2014 by the Geophysical Center RAS.