RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 12, ES5003, doi:10.2205/2012ES000522, 2012
V. G. Getmanov
Geophysical Center RAS, Moscow, Russia
.The article deals with the problem of recognition of anomalies in time series with Raleigh- and tsunami-wave disturbances in signals from hydrostatic pressure sensors (HPS) of ocean bottom seismic stations in the framework of tsunami warning problem. The proposed method of spectral-time analysis (STAN) of signals from the sensors was based on computing the evaluations of functions of frequency-time distribution, decision-making procedures and non-linear filtering for the above problem. The developed STAN method was applied to recognize time intervals with Rayleigh and tsunami-wave disturbances in HPS signals. The proposed STAN method is quite universal and can be used to solve problems of recognition of anomalies in time series of geophysical data of different nature.
Recognition of time series in geophysical data, resulting from various geophysical processes, is one of the most important areas in modern physics of the Earth. Typically, activation of geophysical processes manifests itself in the formation of anomalies in time series of geophysical data. Thus, short-time sections in seismograms, corresponding to the processes of earthquakes, are frequently seen as abnormal, and time series of the Earth's magnetic field magnetograms, correlating to the processes of magnetic storms, also can be interpreted as anomalies.
The general principles of the task of recognition of anomalies in time series of geophysical data refer to [Gvishiani and Dubois, 2002]. In the works [Agayan et al., 2005; Bogoutdinov et al., 2010; Gvishiani et al., 2008] the methods of recognition of anomalies in time series of geophysical data (magnetic in general) were developed. The methods were based on a nonstandard approach, which combines a significant expansion of the initial requirements for the objects of recognition and several provisions of the problem in terms of fuzzy mathematics.
The article confirms the results, obtained in the above works and describes the recognition task from the standpoint of spectral-time analysis (STAN) [Boashash, 2003; Cohen, 1989; Hlawatch and Auger, 2008], which is an effective tool for the study of non-stationary vibration signals. It should be noted that different STAN methods have been successfully used in geophysics, for example, [Dzienovski et al., 1969; Kedrov and Kedrov, 2006; Kedrov et al., 1998; Lander et al., 1973]. The present article is an attempt to combine STAN with decision-making procedures and the subsequent non-linear filtering. The article's results are aimed at solving the problem of automatic detection of geophysical signals and are close to the content of the work [Baranov, 2007], which describes an alternative technology based on wavelet transforms.
The algorithms of recognition, described in the article, make it possible to compare the results of recognition of anomalies based on fuzzy mathematics, wavelet transforms and the proposed STAN method.
Recognition of time series with Raleigh- and tsunami-wave disturbances (further, LR and TW-disturbances) in signals from hydrostatic pressure sensors (HPS) of ocean bottom seismic stations (BSS), containing signals from earthquakes and tsunamis, is an actual task of geophysics. Raleigh waves are formed in the foci of earthquakes, they are distributed on the bottom surface; HPS signals with such components are early precursors of tsunami. Tsunami-wave disturbances, detected in HPS signals from BSS, which are located far away from the shore, may be taken as direct precursors of a tsunami.
BSS with HPS have many advantages over traditional bottom stations, which are equipped with seismographs [Bashilov et al., 2008]. Certain information on the characteristics of signals and the construction of the BSS with HPS are given in [Dykhan et al., 1981; Kulikov and Gonzales, 1995; Levin and Nosov, 2005]. Detailed information about the construction of American BSS with HPS of DART-2 type (Deep-ocean Assesment and Reporting of Tsunami) is placed on the site [www.ndbc.noaa.gov]. BSS, integrated into the global system [www.ndbc.noaa.gov], can provide an effective tsunami warning and make a significant contribution to the study of seismicity of the Earth. These statements are based on the fact that $\approx 80\%$ of all earthquakes occur beneath the bottom of the oceans and seas, and a network of exclusive land-based seismic stations cannot record earthquakes without gaps.
The present article describes a system of sequential algorithms, providing recognition of time series with Rayleigh- and tsunami-wave disturbances in the records of BSS signal. The first STARTS-1 algorithm (Spectral-Time Analysis of Rayleigh-waves and Tsunami-waves Signals) calculates the evaluation of time-frequency distributions (TFD) functions and implements the decision making procedure (d.m.p.) for recognition by comparing the evaluations and reference TFD functions. The second STARTS-2 algorithm produces a non-linear filtering of the d.m.p. results to improve the accuracy of estimating the boundaries of the anomalous areas and to reduce the probabilities of false alarms and omissions.
Some results of this work are described in [Getmanov et al., 2011]. The material of this work in a certain way correlates with [Chebrov and Gusev, 2010; Poplavsky et al., 1988].
The records of signals of the National Geophysical Data Center (NGDC-USA) were used, available in the Internet [www.ngdc.noaa.gov]. For the calculations the record of HPS signal from the DART-2 buoy 46,419, located in the northern part of the U.S. West Coast (coordinates 48.4785° N, 129.3593° W) at a depth of $\approx 4138$ m, was used. The period of record was $\approx 3.5$ years (2006.10.25–2010.03.11), quantization step $T=15$ s, recording capacity $\approx 7,000,000$ numbers. The measurement accuracy of HPS from DART-2 has adopted a value of about 1 mm of water column [www.paroscientific.com].
 |
| Figure 1 |
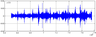
Figure 1 shows the implementation of the oscillation signal $y(Ti)$, obtained after filtration of the additive low-frequency tidal components in the HPS signal for the points $6,503,000 \le i \le 7,752,000$; units of measurement – meters of water column. Observations dates: 2009.08.25, 21 h. 20 min.$\,$–$\,$2010.03.30, 17 h. 25 min. The number of points for the signal in Figure 1 was 1,249,000, the period of observations $\approx 216.8$ days. It was clear that the values of noise components of pressure in the HPS signal were equal, on average, to $3\div 5$ mm. Several time series of the observed signal $y(Ti)$ corresponded to different variants of disturbances.
Let us consider the variants of disturbances, observed in HPS signals. Let us use the information on the physics of signals [Meining et al., 2005; Tompson, 2009] and online materials [www.ngdc.noaa.gov]. The implemented version of disturbance in the first approximation can relate to a certain time in the signal area.
2.1. Disturbance for variant 1 related to the Raleigh (LR) wave processes. LR-disturbances in the signal occur due to submarine earthquakes (sometimes terrestrial earthquakes) and Rayleigh surface transverse waves that propagate on the bottom surface at a speed of 2000–3000 m s$^{-1}$. LR-disturbances in the observed signal are caused by pressure fluctuations of the aquatic environment due to seismic effects in the vicinity of BSS.
 |
| Figure 2 |
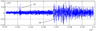
Figure 2 shows the signal $y(Ti)$for the points $6,703,100 \le i \le 6,709,900$, which allows to see the LR-disturbance at a larger scale, registered by BSS as oscillation impulses in the area of the points $6,704,100 \le i \le 6,704,250$.
 |
| Figure 3 |
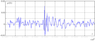
Figure 3 shows the same signal $y(Ti)$ for $6,704,165 \le i \le 6,704,340$ at a larger scale. An oscillatory impulse of the LR-disturbance can be seen, related to the average point $i\approx 6,704,200$. The LR-disturbance consists of a number of high-frequency oscillations with increasing and then decreasing amplitudes; LR-disturbance, in this case, takes time, approximately equal to 375 s.
 |
| Figure 4 |
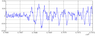
2.2. The disturbance for variant 2 is related to tsunami waves–TW-random oscillations, with durations, which are equal, on average, from $100\div 300$ to $3000 \div 5000$ points ($(1500 \div 4500)- (4500 \div 7500)$ s). In Figure 2 the TW-disturbance corresponds to the section with the points $\approx 6,706,750 \le i \le 6,708,000$. A TW-disturbance is caused by wave oscillations at the vicinity of BSS. The reason of oscillations relates to seismic vertical oscillatory motions of the ground near the earthquake source, which are then transferred into the aqueous medium and distributed in the water at a rate of 200 m s$^{-1}$. As a general rule, sites with LR- and TW-disturbances in the observed signals are separated in time due to their different propagation velocities. Figure 4 on a larger scale shows a TW-disturbance, which begins at the points $i\approx 6,706,750$. We see that a TW-disturbance corresponds to low-frequency oscillations. When considering at a fine time scale, a TW-disturbance is characterized by a sharp leading edge and a flat trailing edge.
2.3. In case of the variant 3, the disturbance is of a double nature. CGM-oscillations–Continuous Ground Motion – are caused by micro-seismic broadband noise from the bottom surface. TWGM (TW + Ground Motion) oscillations are caused by a combination of a tsunami wave and random noise of seismic effects on the bottom surface. The amplitudes of oscillations for TWGM-disturbances can vary widely; TWGM-disturbances are implemented at sufficiently large time intervals. In Figure 2 the intervals $6,703,100 \le i \le 6,704,100$; $6,704,250 \le i \le 6,706,750$ correspond to CGM-disturbances, TWGM-disturbances correspond to points $i>6,708,000$. In a number of cases, TWGM-disturbances are a continuation of TW-disturbances. CGM and TWGM-disturbances, in general, are broadband random oscillations.
It must be kept in mind that a real picture, consisting of a set of options for disturbances in the observed signals from the BSS can be quite complicated, for example, when registering vibrations from several simultaneous earthquakes, etc.
LR and TW-oscillations differ in their frequency characteristics from CGM and TWGM-oscillations; they take significantly less time than CGM and TWGM-oscillations. Therefore, in relation to the entire signal, time series with LR, and TW-disturbances, for further convenience of terminology will be interpreted as anomalies.
In this paper we consider the problem of recognition of time series with anomalies of Rayleigh and tsunami-wave disturbances in HPS signals. These signals are non-stationary with time-varying spectral characteristics. For their recognition we use the STAN algorithm combined with the d.m.p. algorithms and nonlinear filtering.
We present the necessary information from the spectral-time analysis (STAN) and formulate the general problem of recognition. Let us consider the model descriptions of the initial signal and anomalies for the continuous case.
 |
| Figure 5 |
We assume that the initial HPS signal $x(t)$, which generates time series of geophysical data, is defined on a time interval of observation $t_{0} \le t\le t_{f} $. We also assume that anomalous disturbances in the signal are located in the sections, which are given by initial and final moments of time $(t_{1l}, \, t_{2l} )$, $l=1,2, \ldots, L$ – the number of anomalies, Figure 5.
The moments of time $t$, not located in the anomalous sections, will be considered as belonging to non-anomalous sections of the records. Thus we can assume that the initial time interval $t_{0} \le t\le t_{f}$ consists of sets of anomalous and non-anomalous sections.
For the signal $x(t)$ we make a provision for its frequency representation based on the Fourier transform $C (j\omega)$. The basis of the STAN algorithm consists of the so-called functions of time-frequency distributions (TFD) $P(\omega ,t)$, defined in the simplest case, in the rectangle $\omega \in \Omega,$ $t\in T$, $T=\{ t:(t_{0} \le t\le t_{f} )\}$, $\Omega =\{ \omega :(\omega _{0} \le \omega \le \omega _{f} )\} $. The TFD functions are functions of two variables – time and frequency. The physical meaning of TFD functions follows from the relations
\begin{eqnarray*} P(\omega ,t) dt d\omega =dE \end{eqnarray*} \begin{eqnarray*} \int _{-\infty }^{\infty } \int _{-\infty }^{\infty } P (\omega ,t) dt d\omega = E \end{eqnarray*}which determine a value $dE$ of a signal energy attributable to a time interval $(t,t+dt)$ and frequency range $(\omega ,\omega +d\omega )$, and the total energy of signal $E$ . It should be noted that the TFD function and value of the instantaneous signal power calculated in the time and frequency domains are connected by the obvious relations
\begin{eqnarray*} \int _{-\infty }^{\infty }P (\omega ,t)dt=\left|C(j\omega )\right|^{2} \end{eqnarray*} \begin{eqnarray*} \int _{-\infty }^{\infty }P (\omega ,t)d\omega =\left|x(t)\right|^{2} \end{eqnarray*}Let us introduce, using the time points $t_{n}$, $n=1, \ldots, \,n_{0}$, $t_{n_{0}} =t_{f}$ small local time intervals $dt_{n} =\{ t:(t_{n-1} \le t\le t_{n} )\}$ for $t_{0} \le t\le t_{f} $. Let us determine in local intervals $\omega \in \Omega$, $t\in dt_{n} $ the local TFD functions $P_{n} (\omega ,t)$, which are equal to zero outside the local intervals – $P_{n} (\omega ,t)=0$, for $t\notin dt_{n}$. The relation $P(\omega ,t)=\sum _{n=1}^{n_{0} }P_{n} (\omega ,t)$ must be fulfilled, and its physical meaning is obvious. TFD function can be discrete in time and frequency $P(\omega _{k}, \; t_{n} )$
\begin{eqnarray*} P_{k,n} (\omega ,t)=P(\omega_{k} ,t_{n} ), \quad \omega_{k-1} \le \omega \le \omega_{k} , \quad t_{n-1} \le t\le t_{n} \end{eqnarray*} \begin{eqnarray*} P_{k,n} (\omega ,t)=0, \quad \omega < \omega _{k-1} , \quad \omega > \omega _{k} , \quad t < t_{n-1} , \quad t > t_{n} \end{eqnarray*} \begin{eqnarray*} P(\omega ,t)=\sum_{k=1}^{k_{0} }\sum _{n=1}^{n_{0} }P_{k,n} (\omega ,t) \end{eqnarray*}At the same time we introduce the normalized TFD functions $\bar{P}(\omega _{k} ,t_{n})$ and formulate the restricting set for the indices $(k,n)\in \Xi $ and the optimization task
\begin{eqnarray*} (k^{\circ } ,n^{\circ } )=\arg \{ \mathop{\max }\limits_{k,n\in \Xi } P(\omega _{k} ,t_{n} )\} \end{eqnarray*} \begin{eqnarray*} \bar{P} (\omega_{k} , t_{n} ) = P(\omega_{k} ,t_{n} )/ P(\omega_{k^{\circ }} ,t_{n^{\circ }} ) \end{eqnarray*}Let us consider the signal $x(t)$, for which the definition of anomalous and non-anomalous time series will be based on local TFD functions' evaluations $P_{n}^{\circ } (\omega ,t)$. We assume that anomalous and non-anomalous time series are determined by evaluations of local TFD functions with different spectral characteristics. In practice, these situations are fairly common.
Let the local intervals $dt_{n1} $, $dt_{n2} $, $dt_{n3} $ correspond to the evaluations of local TFD functions $P_{n1}^{\circ } =P_{n1}^{\circ } (\omega ,t)$, $P_{n2}^{\circ } =P_{n2}^{\circ } (\omega ,t)$, $P_{n3}^{\circ } = P_{n3}^{\circ } (\omega ,t)$. We suppose that the interval $dt_{n1} $ is an anomaly and intervals $dt_{n2} $, $dt_{n3} $ are non-anomalous. We introduce, in the conventional sense, the distance functional $\rho (\cdot ,\cdot )$ between the evaluations of TFD functions that belong to different time series of records. We assume that for local intervals, belonging to non-anomalous series, TFD functions' evaluations are almost identical; this means that $\rho (P_{n2}^{\circ } , P_{n3}^{\circ } )\approx 0$. For local intervals, belonging to anomalous and non-anomalous series, the TFD functions differ significantly; this means that $\rho (P_{n1}^{\circ } ,P_{n2}^{\circ } ) \gg 0$, $\rho (P_{n1}^{\circ } ,P_{n3}^{\circ } )\gg 0$.
Thus, the solution to the problem of recognition of anomalies in HPS signals is based on a calculation of local TFD and distance functional. We use the differences in the spectral parameters of signals in anomalous and non-anomalous intervals of time series.
We will use the standard methods of decision-making, which is usually applied to solving problems of statistical radio engineering [Levin, 1989]. Let us use the method, based on pattern recognition in frequency domain [Joswig, 1990; Savchenko, 1997]. Let us assume that a local reference TFD function $P_{0} (\omega ,t)$ is independent of a local interval and is determined by a vector of parameters $P_{0} $. We introduce the functional $\rho_{0} (P_{n}^{\circ } (\omega ,t),P_{0} (\omega ,t))=\rho_{0} (P_{n}^{\circ } (\omega ,t),P_{0} )$, $\omega \in \Omega ,$ $t\in dt_{n} $, equivalent of the distance between the evaluation of a local TFD function and local reference TFD function, which is accepted as a critical functional.
In this case the d.m.p. is based on the calculation of decisive functional for verification of the following conditions: if $\rho_{0} (P_{n}^{\circ } ,P_{0} )=1$ – then a local interval $dt_{n} $ belongs to an anomaly, if $\rho_{0} (P_{n}^{\circ } , \; P_{0} )=0$ – a local interval $dt_{n} $ is located within a non-anomalous section of a record.
Evaluation of boundary coordinates of anomalies is based on the analysis of the d.m.p. results for a sequence of local intervals and is probabilistic in nature. The decision whether a local interval belongs to an anomalous section or not, in practice, is always associated with errors: sometimes it is decided that an interval belongs to an anomalous section, and in reality it doesn't, and vice versa.
Formulation of the recognition problem comprises two components.
$\bullet$ Evaluation of coordinates of the boundaries of anomalies $(t_{1l}^{\circ } ,t_{2l}^{\circ } ), \quad l=1,2, \ldots, L^{\circ }$;
$\bullet$ Evaluation of a probability of anomalies in the intervals $(t_{1l}^{\circ }, t_{2l}^{\circ } ), \quad \quad p_{l}^{\circ }, \quad l=1,2, \ldots, L^{\circ }.$
Let us proceed from a continuous to a discrete argument. Let us represent a time series of discrete signal as
\begin{eqnarray*} y(Ti)=y(i), \quad N_{0} \le i\le N_{f} \end{eqnarray*}where $N_{0}$, $N_{f} $ are the numbers of the initial and final points of an initial signal $x(t)$, $T$ – a quantization step. We introduce a system of local intervals. Let $dN$ be a number of points in a local interval and the number of the local boundary points of intervals satisfy the equations
\begin{eqnarray*} N_{1n} =N_{0} +(n-1)dN \end{eqnarray*} \begin{equation} \tag*{(1)}\label{1} N_{2n} =N_{1n} +dN-1, \quad n=1,\ldots, n_{0} \end{equation}where $n_{0} $ – number of local intervals, $n_{0} =\mbox{ent}((N_{f} -N_{0} )/dN)$, function ent$(\cdot )$ – the integer part. Points, satisfying the condition $N_{1n} \le i\le N_{2n} $ belong to the local interval $n$.
Let us consider the computing of sliding discrete Fourier transforms (DFT) [Lyons, 2007] for an initial signal. Each local interval will correspond to a $N$-points DFT-sliding interval. For the DFT-sliding interval with the step of sliding $dN$ we assign the boundary points $\bar{N}_{1n}$, $\bar{N}_{2n} $. The interval corresponds to the local interval $n$
\begin{equation} \tag*{(2)}\label{2} \bar{N}_{1n} =N_{1n} -(N-dN)/2, \quad \bar{N}_{2n} =\bar{N}_{1n} +N-1 \end{equation}Let us formulate observations in the DFT-sliding intervals
\begin{eqnarray*} y_{n} (s)=y(\bar{N}_{1n} +s) , \quad s=0,\ldots, N-1, \quad n=1,\ldots,n_{0} \end{eqnarray*}We write the expression for the coefficient of the DFT for the signal points in the $n$-th sliding DFT-interval and we apply the weighted Hanning window $W(s),s=0, \ldots,N-1$ [Getmanov, 2010]
\begin{eqnarray*} C_{n} (k)=\frac{1}{N} \sum _{s=0}^{N-1}y_{n} (s)W(s)e^{-j\displaystyle{\frac{2\pi (k-1)s}{N} }} \end{eqnarray*} \begin{equation} \tag*{(3)}\label{3} k=1,\ldots, N/2, \quad n=1,\ldots,n_{0} \end{equation}The index $k$ defines the discrete DFT-frequencies $\Delta \omega =2\pi /NT$, $\omega _{k} =\Delta \omega (k-1)$, $k=1,\ldots,N/2$. We take the expression
\begin{eqnarray*} P^{\circ } (\omega_{k} ,t_{n} )=C_{n}^{*} (k)C_{n} (k), \quad k=1,\ldots,N/2 \end{eqnarray*} \begin{equation} \tag*{(4)}\label{4} n=1,\ldots,n_{0}, \quad P^{\circ } (k,n)= P^{\circ } (\omega_{k} ,t_{n} ) \end{equation}as the evaluation $P^{\circ } (k,n)$ of a local TFD function in points $k,n$, corresponding to discrete frequencies $\omega_{k} $ and local intervals $t_{n} $.
Let us analyze a HPS signal and consider a kind of TFD functions for sections with LR and TW-disturbances.
 |
| Figure 6 |
Figure 6 shows the evaluation of the normalized TFD function $\bar{P}^{\circ } (k,n)$, corresponding to a case of LR. The interval $6,704,150 \le i \le 6,704,250$ was taken where it was known a priori about a LR-disturbance; we used the $N=32$-dimensional DFT for calculating the TFD with sliding step $dN=2$. Figure 5 shows that the values of evaluated TFD are concentrated in a high-frequency area for indices $k\approx 10-16$.
 |
| Figure 7 |
Figure 7 shows the normalized TFD function $\bar{P}^{\circ } (k,n)$, corresponding to a TW case. The interval $6,707,125\le i \le 6,707,205$ was examined, the TFD dimension $N=32$, sliding step $dN=2$. We see that the TFD values are concentrated in a low-frequency area for indices $k\approx 1-5$.
It can be concluded from Figure 6 and Figure 7 that LR-disturbances correspond to low-frequency TFD. The conclusions are in compliance with the physics of LR and TW-processes. This conclusion can apply, after analyzing other intervals, to the entire signal $6,000,000\le i\le 7,600,000$.
7.1. Let us consider a case of high-frequency TFD functions, corresponding to LR-disturbances. Let $\bar{P}_{1R}$, $\bar{P}_{2R}$, $k_{0R}$, $N$, $P_{3R}$ be the configuration parameters for the proposed d.m.p. The first four parameters $\bar{P}_{1R}$, $\bar{P}_{2R}$, $k_{0R}$, $N$ determine a reference normalized TFD function, the parameter $P_{3R} $ defines the maximal value for the TFD function evaluation. We calculate relations for $n=1,\ldots, n_{0}$, in order to formulate a correct d.m.p., $k_{1R} =k_{0R} +1$
\begin{eqnarray*} \bar{P}_{1MR,m} (n)=\mathop{\max \bar{P}_{m}^{\circ } }\limits_{1\le k\le k_{0R} } (k,n) \end{eqnarray*} \begin{eqnarray*} \bar{P}_{2MR,m} (n)=\mathop{\max \bar{P}_{m}^{\circ } }\limits_{k_{1R} \le k\le N/2} (k,n) \end{eqnarray*} \begin{equation} \tag*{(5)}\label{5} P_{3MR,m} (n)=\mathop{\max P_{m}^{\circ } }\limits_{1\le k\le N/2} (k,n) \end{equation}The proposed d.m.p., providing that the $n$ local interval belongs to an anomalous section with a LR-disturbance, is related to computing the logical expression $P_{R} (n)$ using (5) for $n=1,\ldots,n_{0} $
\begin{equation} \tag*{(6)}\label{6} P_{R} (n)=(\bar{P}_{1MR,m} (n) < \bar{P}_{1R} )\; \bigcap \; (\bar{P}_{2MR,m} (n) > \bar{P}_{2R} )\; \bigcap \;(P_{3MR,m} (n) > P_{3R} ) \end{equation}The formulae (6) have a quite clear physical meaning In this case the d.m.p. is to check the joint implementation of the inequalities (6) and calculation of the indicator coefficient $I_{R} (n)$: if the logical expression $P_{R} (n)$ (6) is correct, then the value $I_{R} (n)=1$ is accepted; otherwise – $I_{R} (n)=0$.
The sequence $I_{R} (n)$, $n=1,\ldots,n_{0} $, consisting of zeros and ones, is divided into $m_{0} $ indication intervals of equal size, equal to $dN_{R} $, $m_{0} dN_{R} =n_{0} $. Initial and final points of an indication interval with the number $m$ can be calculated in the obvious way:
\begin{eqnarray*} N_{1R} (m)=N_{0} +dN_{R} (m-1) \end{eqnarray*} \begin{equation} \tag*{(7)}\label{7} N_{2R} (m)=N_{1R} +dN_{R}, \quad m=1,2,\ldots, m_{0} \end{equation}Using (7) and the values $I_{R} (n)$ the LR-indication function $\alpha _{0R} (m)$ is calculated for each indication interval
\begin{equation} \tag*{(8)}\label{8} \alpha _{0R} (m)= \frac{1}{dN_{R} } \sum_{n=N_{1R} (m)}^{N_{2R} (m)}I_{R} (n) , \quad m=1,2,\ldots, m_{0} \end{equation}
7.2. Similarly, let us consider a case of low-frequency TFD functions, corresponding to TW-disturbances. Let $\bar{P}_{1T} ,\bar{P}_{2T} ,k_{0T}, N, P_{3T} $ be setup parameters. For $n=1,...,n_{0} $ we calculate the relations for TW, $k_{1T} =k_{0T} +1$
\begin{eqnarray*} \bar{P}_{1MT,m} (n)=\mathop{\max \bar{P}_{m}^{\circ } }\limits_{1\le k\le k_{0T} } (k,n) \end{eqnarray*} \begin{eqnarray*} \bar{P}_{2MT,m} (n)=\mathop{\max \bar{P}_{m}^{\circ } }\limits_{k_{1T} \le k\le N/2} (k,n) \end{eqnarray*} \begin{equation} \tag*{(9)}\label{9} P_{3MT,m} (n)=\mathop{\max P_{m}^{\circ } }\limits_{1\le k\le N/2} (k,n) \end{equation}The proposed d.m.p. related to the fact that the local interval $n$ belongs to an anomalous section with a TW-disturbance is implemented on the basis of calculating the local expression $P_{T} (n)$ for $n=1,\ldots,n_{0} $
\begin{equation} \tag*{(10)}\label{10} P_{T} (n)=(\bar{P}_{1MT,m} (n) > \bar{P}_{1T} ) \; \bigcap \; (\bar{P}_{2Mt,m} (n) < \bar{P}_{2T} ) \; \bigcap \; (P_{3MT,m} (n) > P_{3T} ) \end{equation}The formulae (10), same as (6), are quite obvious and can be used for computing the indication coefficient $I_{T} (n)$: if the logical expression $P_{T} (n)$ (10) is true, then $I_{T} (n)=1$; otherwise – $I_{T} (n)=0$. The resulting sequence $I_{T} (n)$, $n=1,\ldots,n_{0} $ is divided into $dN_{T} $, $m_{0} dN_{T} =n_{0} $ – dimensional $m_{0} $ indicator intervals. Initial and final points of the indication interval $m$ can be calculated in a similar way (7):
\begin{eqnarray*} N_{1T} (m)=N_{0} +dN_{T} (m-1) \end{eqnarray*} \begin{equation} \tag*{(11)}\label{11} N_{2T} (m)=N_{1T} +dN_{T}, \quad m=1,2,\ldots,m_{0} \end{equation}Applying (7) and $I_{T} (n)$ we calculate the TW-indication function $\alpha _{0T} (m)$ for each indication interval
\begin{equation} \tag*{(12)}\label{12} \alpha_{0T} (m)=\frac{1}{dN_{T} } \sum_{n=N_{1T} (m)}^{N_{2T} (m)}I_{T} (n) , \quad m=1,2,\ldots,m_{0} \end{equation}The indication functions $\alpha_{0R} (m)$, $\alpha_{0T} (m)$ can be interpreted as the probability of the presence of LR and TW-disturbances at the indication interval $m$. Calculation of indication functions is connected with calculation of indicator functions associated with probability errors – possible false detection and omissions (probabilistic errors).
TFD functions evaluation (paragraph 5), implementation of d.m.p. and calculation of indication functions (paragraph 7) is made on the basis of STARTS-1 algorithm.
To reduce the size of the text, the index "p" in the formulae will take two values: 1. "$p$"$ = R$; 2. "$p$"$ = T$, and correspond to the cases of LR and TW-disturbances.
The initial data for the implementation of the nonlinear filtering algorithm – the d.m.p. results are presented as the indicator function $\alpha_{0p} (m)$, $m\in M$, $M=\{ m:(1\le m\le m_{0} )\} $ from (8) or (12). The purpose of nonlinear filtering of indicator functions is to improve the accuracy of the boundaries of anomalous intervals and probabilities evaluations. The proposed algorithm for nonlinear filtering of indicator functions is based on threshold filtering algorithms and algorithms for filtering pulse sequences with pulse modulation, known from radio engineering [Baskakov, 2005; Gonorovsky, 2006]. To a certain extent, this algorithm is heuristic, it requires a selection of configuration parameters and possible improvements. The implementation of nonlinear filtering is based on the STARTS-2 algorithm.
8.1. The first stage of the algorithm consists of realization of the nonlinear amplitude filtering of indicator function and is related to removing the small values from the sequence $\alpha _{0p} (m)$, $m\in M$, $M=\{ m:(1\le m\le m_{0} )\}$. Removal of small values is done on the basis of comparison with the threshold $\alpha _{0p} $, and the sequence's formation $\alpha_{1p} (m)$, $m\in M$
\begin{eqnarray*} \alpha _{1p} (m)=0, \mbox{ if } \alpha _{0\delta} (m)<\alpha _{0p} \end{eqnarray*} \begin{equation} \tag*{(13)}\label{13} \alpha _{1p} (m)=\alpha _{0p} (m), \mbox{ if } \alpha _{0\delta} (m)\ge \alpha _{0p} , m\in M \end{equation}The threshold's value parameter is adjustable and its correct choice ensures the optimal correlation between the probabilities of detection and error.
8.2. The algorithm's second stage relates to implementation of non-linear time-latitude filtering of indicator function and is related to removing sites with a small amount of zero and positive values in the sequence from the first stage $\alpha_{1p} (m)$.
For implementation of the second stage we use a function $\Psi \{ \cdot ,\cdot \} $, which calculates bordering points of intervals with zero and positive values of sequence elements of a certain input sequence $y(m),m\in M$ and the corresponding numbers of these intervals. In general, we get
\begin{eqnarray*} \Psi \{ y(m), \,m\in M \} =\{ (m_{1,l0} m_{2,l0} ), \quad l0=1,...,L_{0}, \end{eqnarray*} \begin{eqnarray*} (m_{1,l1} , m_{2,l1} ), \quad l1=1,...,L_{1} \} \end{eqnarray*}where $(m_{1,l0} ,m_{2,l0} )$ – bordering points of intervals with zero elements, $L_{0} $ – number of intervals with zero elements, $(m_{1,l1} ,m_{2,l1} )$ – bordering points of intervals with positive elements, $L_{1} $ – number of intervals with positive elements. The calculations on the function $\Psi \{ \cdot ,\cdot \} $ are done with the help of the CABORD (Calculation of Borders) algorithm.
Let us apply the function $\Psi \{ \cdot ,\cdot \} $ to $\alpha_{1p} (m)$, we find the bordering points of intervals with positive elements and the corresponding numbers of these intervals
\begin{equation} \tag*{(14)}\label{14} \Psi \{ \alpha_{1p} (m),m\in M \} =\{ (m_{1,l1} ,m_{2,l1} ), \quad l1=1,\ldots,L_{1} \} \end{equation}Further, on the basis of (14) the set $L1$ of the intervals' numbers can be found, which satisfy the inequality $(m_{2,l1} -m_{1,l1} )< dm_{1p} $, where $dm_{1p} $ is the setup parameter. Then the corresponding set $M1$ is formed on the basis of indices $m$
\begin{eqnarray*} L1= \{ l1:(m_{2,l1} -m_{1,l1} < dm_{1p}, \quad l1=1,\ldots,L_{1} )\} \end{eqnarray*} \begin{equation} \tag*{(15)}\label{15} M1=\{ m:(m_{1,l1} \le m\le m_{2,l1} , \quad l1\in L1)\} \end{equation}on its basis the interim sequence $\alpha_{2p} (m)$ is formed, where single (or rare) positive values in $\alpha _{1p} (m)$ are replaced by zeros
\begin{eqnarray*} \alpha_{2p} (m)=0, \quad m\in M1 ; \end{eqnarray*} \begin{equation} \tag*{(16)}\label{16} \alpha_{2p} (m)=\alpha_{1p} (m), \quad m\in M/M1 \end{equation}After that intervals with a small number of zeros are removed from the sequence $\alpha_{2p} (m)$. For this purpose the function $\Psi \{ \cdot ,\cdot \}$ is used again for $\alpha_{2p} (m)$, $m \in M$, for which the borders of intervals with zero elements are defined
\begin{equation} \tag*{(17)}\label{17} \Psi \{ \alpha_{2p} (m), m\in \} =((m_{1,l0}, m_{2,l0} ), \quad l0=1, \ldots,L_{0} ) \end{equation}and from (17) the corresponding sets $L0,M0$ are found, taking into account the setup parameter $dm_{2p} $.
\begin{eqnarray*} L0=\{ l0:(m_{2,l0} -m_{1,l0} < dm_{2p}, \quad l0=1,...,L_{0} )\} \end{eqnarray*} \begin{equation} \tag*{(18)}\label{18} M0=\{ m:(m_{1,l0} \le m\le m_{2,l0} ,l0\in L0)\} \end{equation}The result of the non-linear filtering is represented as the sequence $\xi_{p}^{\circ } (m)$
\begin{eqnarray*} \xi_{p}^{\circ } (m)=\alpha _{0p} (m), \quad m\in M0 \end{eqnarray*} \begin{equation} \tag*{(19)}\label{19} \xi _{p}^{\circ } (m)=\alpha_{2p} (m), \quad m\in M/M0 \end{equation}The solution of our problem of recognition of abnormal areas is based on algorithms for evaluation of the boundaries of abnormal areas and calculation of the probabilities.
The result of the filtering $\xi_{p}^{\circ } (m)$ is used, which is transformed by the function $\Psi \{ \cdot ,\cdot \} $, with the purpose to find the sequence of borders of intervals with positive elements $(m_{1,l}^{\circ } ,m_{2,l}^{\circ } )$, $l=1,\ldots, L^{\circ }$
\begin{eqnarray*} \Psi \{ \xi _{p}^{\circ } (m),m\in M\} =(m_{1,l}^{\circ } ,m_{2,l}^{\circ } ), \quad l=1,\ldots,L_{}^{\circ } , \end{eqnarray*} \begin{equation} \tag*{(20)}\label{20} i=N_{0} +(m-1)dN_{0} , (i_{1,l}^{\circ } ,i_{2,l}^{\circ } ), \quad l=1,\ldots,L_{}^{\circ } \end{equation}Evaluation of probabilities of anomalies in the intervals $(m_{1,l}^{\circ } ,m_{2,l}^{\circ } )$, $l=1,\ldots,L^{\circ } $, is done by the following obvious formulae
\begin{eqnarray*} p_{lp}^{\circ } =(\sum_{m=m_{1,l}^{\circ } }^{m_{2,l}^{\circ } }\alpha_{0p} (m) ) / (m_{2,l}^{\circ } -m_{1,l}^{\circ } +1), \end{eqnarray*} \begin{equation} \tag*{(21)}\label{21} l=1,\ldots,L^{\circ }, \quad \alpha_{lp} =p_{lp}^{\circ } \end{equation}Calculation of the indicator function $\alpha_{p} (i)$ for $N_{0} \le i\le N_{f} $ is done by using (21)
\begin{eqnarray*} \alpha_{lp} (i)=p_{lp}^{\circ } \mbox{ for } i\in (i_{1,l}^{\circ } ,i_{2,l}^{\circ } ), \end{eqnarray*} \begin{eqnarray*} \alpha_{lp} (i)=0 \mbox{ for } i\notin (i_{1,l}^{\circ } ,i_{2,l}^{\circ } ), l=1,\ldots,L^{\circ }, \quad \end{eqnarray*} \begin{equation} \tag*{(22)}\label{22} \alpha_{p} (i)=\sum_{l=1}^{L_{p}^{\circ } }\alpha_{lp} (i) \end{equation}Thus, the STAN method for the present task of recognition led to a sequential application of the STARTS-1 and STARTS-2 algorithms. Let us describe the procedure.
In accordance with the STARTS-1 algorithm local TFD functions are evaluated and implementation of the d.m.p. coming to actions 1–3, which are related to:
For the STARTS-1 algorithm we list: input variables – $N_{0} ,N_{f} $, $dN$, $N$, $y(i),N_{0} \le i\le N_{f} $; setup parameters – $\bar{P}_{1R}$, $\bar{P}_{2R}$, $k_{0R}$, $P_{3R}$; output variables – $\alpha_{0R} (m)$, $\alpha_{0T} (m)$, $m=1,2,\ldots,m_{0} $.
On the basis of the STARTS-2 algorithm the non-linear filtering of indicator functions is done, which is reduced to steps 1–3, which in their turn comprise:
For the STARTS-2 algorithm we list: input variables – $\alpha _{0p} (m)$, $m=1,2,\ldots,m_{0} $; setup parameters – $\alpha_{0p}$, $dm_{1p}$, $dm_{2p}$; output variables – $\xi_{p}^{\circ } (m)$, $m=1,2,\ldots ,m_{0}$, $(m_{1,l}^{\circ } ,m_{2,l}^{\circ } )$, $l=1,\ldots,L^{\circ }$, $p_{lp}^{\circ }$, $l=1,\ldots, L^{\circ }$, $\alpha_{p} (i)$. The STARTS-2 algorithm uses the results of the application of the CABORD algorithm.
We considered the filtered HPS signal $y(i)=y(Ti)$ from NGDC at a fixed time interval; $N_{0} =600,001$, $N_{f} =7,600,000$ – numbers of the initial and final point of this interval. The signal was used for testing the developed system of the STARTS-1 and STARTS-2 sequential algorithms for recognition of anomalies in time series with LR and TW-disturbances. The results of the algorithms' application were compared to the control data, received from NGDC.
10.1. Recognition of time series with LR-disturbances was implemented. A fixed time interval was divided into $n_{0} =3,500,000$ $dN=2$-dimensional local intervals. Each of the local interval corresponded to DFT-sliding intervals with dimension $N=32$. $dN_{R} =20$ – number of points of an indicator interval, $m_{0} =175,000$ – number of indicator intervals. The fixing parameters for d.m.p. took the values: $\bar{P}_{1R} =0.10$, $\bar{P}_{2R} =0.3$, $P_{3R} =0.0005$, $k_{0R} =10$. For the setup parameters of non-linear filtering we took the values $\alpha _{R0} =0.4$, $dm_{1R} =2$, $dm_{2R} =2$.
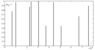 |
| Figure 8 |
Figure 8 shows the results of the algorithm's application in the form of a graph of the indicator function $\alpha_{R} (i)$, representing a set of vertical lines of different height.
 |
| Table 1 |
Table 1 comprises the data on recognition of LR-disturbances. Columns 2, 3 show the coordinates of the bordering points of intervals with LR-disturbances from NGDC $(i_{1}$NGDC, $i_{2}$NGDC), which were calculated with the help of a semi-automatic NGDC-algorithm, based on the analysis of signals in time domain. Columns 4, 5 show the coordinates of the bordering points of intervals with LR-disturbances, calculated by the system of algorithms, proposed by Organization of the Russian Academy of Sciences Geophysical Center (GC RAS). Column 6 shows the evaluations of probabilities of LR-disturbances $\alpha_{lR} $ in the intervals with calculated bordering points $(i_{1,l} ,i_{2,l} )$, $l=1,\ldots,L_{0}$, $L_{0} =13$.
We note that the intervals $\#5-7$ with LR-disturbances, according to Table 1, have been recognized (their time resolution was realized); however, in Figure 7 these intervals are shown together. The proposed algorithm has implemented a sufficiently precise recognition of almost all the marked LR-disturbances. It should be noted that in interval $\#11$, in the points $6,704,179\le i\le 6,704,246$, mentioned by NGDC, there was really a LR-disturbance, which was weaker than another LR-disturbance, located in the interval $6,751,311\le i\le 6,751,352$.
10.2. Recognition of time series with TW-disturbances. A fixed time interval was divided into $n_{0} =1,750,000$ local intervals of the dimension $dN=4$. Each of the local intervals corresponded to DFT-sliding intervals of the dimension $N=32$. We assumed that $dN_{T} =25$ was the number of points of the indicator interval, $m_{0} =70,000$ – the number of indicator intervals. The setup parameters for d.m.p. took the values: $\bar{P}_{1T} =0.5$, $\bar{P}_{2T} =0.125$, $P_{3T} =0.004$, $k_{0T} =5$. The values of setup parameters of non-linear filtering were $\alpha _{T0} =0.4$, $dm_{1T} =2$, $dm_{2T} =2$.
 |
| Figure 9 |
Figure 9 shows the graph of the indicator coefficient $\alpha_{T} (i)$ as a set of vertical lines of different height. Their intersection with the horizontal axis of coordinates determines the time boundary points of intervals with TW-disturbances.
 |
| Table 2 |
Table 2 shows the data on recognition of TW-disturbances. Columns 2, 3 contain the coordinates of the bordering points of TW-intervals, determined on the basis of the semi-automatic recognition algorithm, based on the analysis of signals of time series. The algorithm was developed by NDBC and the data was transferred to GC RAS. Columns 4, 5 show the coordinates of the bordering points of TW-intervals, obtained on the basis of the algorithms of recognition, developed by GC RAS. Column 6 contains the evaluations of probabilities of recognition of TW-disturbances $\alpha_{Tl} $ in the intervals with calculated bordering points $(i_{1,l}$, $i_{2,l} )$, $l=1,\ldots,L_{0}$, $L_{0} =4.$
The proposed STAN method for recognition of time series with LR and TW-disturbances, if we analyze the results of Figure 8 and Figure 9 and Table 1 and Table 2, works quite well. Thus, for $ 13+4=17 $ disturbances the proposed algorithms allowed only one false disclosure and one omission, that allows us to conclude, at a first approximation, that the level of false disclosures and omissions was equal to $\approx 5.8\%$.
The effectiveness of the STAN method of recognition of time series with LR and TW-disturbances in terms of minimizing the probability of false detections and omissions, as well as possible refinements of the boundary points of anomalies can be improved by optimizing the choice of setup parameters. Due the adequate mathematical apparatus of TFD functions, the proposed STAN method and the corresponding algorithms have the potential to provide detection of weak LR and TW-disturbances.
The proposed STAN method of recognition can be used to automate the viewing of archives records of observations from the BSS network and to ensure the efficient solution of the tsunami warning problem.
The developed method of STAN-recognition is quite versatile and enables the solution of problems of recognition of anomalies in time series of geophysical data of different nature.
Agayan, S. M., S. R. Bogoutdinov, A. D. Gvishiani, E. M. Graeva, J. Zlotnicki, M. V. Rodkin (2005), Study of signal's morphology on the basis of fuzzy logic algorithms, Geophysical Studies, 1, 1, 143–155.
Baranov, S. V. (2007), Application of wavelet-transform for automatic detecting of seismic signals, Fizika Zemli, 2, 83–94.
Baskakov, S. I. (2005), Radio Engineering Networks and Signals, Moscow, Vyshaya Shkola, 462.
Bashilov, I. P., et al. (2008), Ocean-bottom geophysical observatories – methods of construction and fields of application, Nauchnoe Priborostroenie, 18, 2, 86–97.
Boashash, B. (2003), Time Frequency Signal analysis and processing, Elsevier Science, 770.
Bogoutdinov, S. R., A. D. Gvishiani, S. M. Agayan, A. A. Soloviev, E. Kihn (2010), Recognition of disturbances with given morphology in time series I. spikes on INTERMAGNET magnetic records, Fizika Zemli, 11, 99–112.
Chebrov, D. V., A. A. Gusev (2010), Automatic definition of parameters of tsunami generating earthquakes in the russain Far East in real time: Algorithms and software, Seismicheskie Pribory, 46, 3, 5–21.
Cohen, L. (1989), Time-frequency distributions: review, TIIER, 77, 10, 72–120.
Dykhan, B. D., V. M. Zhak, E. A. Kulikov (1981), First tsunami registering in open ocean, DAN, 257, 5, 1088–1092.
Dzienovski, A., S. Bloch, M. Landisman (1969), Technique for the analysis of transient seismic signals, Bull. Seismol. Soc. Amer., 59, 427–444.
Getmanov, V. G. (2010), Digital Processing of Signalds, Moscow, NIYaU MIFI Publishers, 248.
Getmanov, V. G., A. D. Gvishiani, K. Stroker (2011), Recognition of P-waves disturbances in observations of specialized bottom stations. Deep structure, geodynamics, interpretation of geophysical fields, Shestye Nauchnue Chtenija Pamyati Y. P. Bulashevicha, Materialy Konferencii, Ekaterinburg, URO RAN, 76–79.
Gonorovsky, I. S. (2006), Radio Engineering Networks and Signals, Textbook, Moscow, Drofa, 719.
Gvishiani, A., J. Dubois (2002), Artificial Intelligence and Dynamic Systems for Geophysical Applications, Paris, Springer-Verlag, 350.
Gvishiani, A. D., S. M. Agayan, S. R. Bogoutdinov (2008), Definition of anomalies in time series by methods of fuzzy recognition, Doklady RAN, 421, 1, 101–105.
Hlawatch, F., F. Auger (2008), Time-Frequency Analysis: Concepts and Methods, London, ISTE and Wiley, 440.
Joswig, M. (1990), Pattern recognition for earthquake detection, Bulletin of the Seismological Society of Placecountry-Region America, 80, 1, 170–186.
Kedrov, E. O., O. K. Kedrov (2006), Spectral-time method of identification of seismic phenomena at distances $15-40\mbox{°}$, Fizika Zemli, 5, 47–64.
Kedrov, O. K., L. A. Polikarpova, G. M. Steblov (1998), Algorithm of recognition of weak short-period seismic signals on the basis of time-frequency analysis of three-component records in real time regime, Izv. RAN, Fizika Zemli, 2, 30–45.
Kulikov, E. A., F. Gonzales (1995), Restoration of tsunami waveforms at the source by measuring vibration level of ocean by remote hydrostatic pressure sensor, DAN, 344, 6, 814–818.
Lyons, R. (2007), Digital Processing of Signals (Translated from English), Moscow, Binom-Press, 656.
Lander, A. V., A. L. Levshin, V. F. Pisarenko (1973), Spectral-time analysis of oscillations, Vychislitelnaya Seismologija, 6, 3–27.
Levin, B. R. (1989), Theoretical Basics of Statistical Radio Engineering, Moscow, Radio I Svjaz, 665.
Levin, B. R., M. A. Nosov (2005), Physics of Tsunami and Related Phenomena in Ocean, Moscow, Janus-K, 360.
Meining, C., S. Stalin, A. I. Nacamura, F. Gonzalez (2005), Technology development in real-time tsunami measuring, monitoring and forecasting, Proc. IEEE Oceans Conf., Sept. 2005, 2, 1673–1679.
Poplavsky, A. A., E. A. Kulikov, L. N. Poplavsky (1988), Methods and Algorithms of Operative Tsunami Forecasting, Moscow, Nauka. 128.
Savchenko, V. V. (1997), Recognition of random signals in frequency domain, Radiotekhnika I Elektronika, 42, 4, 426–429.
Tompson, S. R. (2009), Sound Propagation Considerations for a Deep-Ocean Acoustic Network, US Naval Academy, 63.
Received 26 July 2012; accepted 29 July 2012; published 12 September 2012.


Citation: Getmanov V. G. (2012), Method of spectral-time analysis for recognition of anomalies in time series with Raleigh- and tsunami-wave disturbances in signals from hydrostatic pressure sensors of ocean bottom seismic stations, Russ. J. Earth Sci., 12, ES5003, doi:10.2205/2012ES000522.
Copyright 2012 by the Geophysical Center RAS.