
T. L. Gulyaeva1
Institute of Terrestrial Magnetism, Ionosphere and Radiowave Propagation, Troitsk, Moscow Region, Russia
1Also at Space Research Center, Warsaw, Poland
The International Reference Ionosphere (IRI) [Rawer et al., 1978] created in the 1970s, has been improved since then in many of its parameters. The model makes it possible to determine ionospheric parameters for quiet midlatitude monthly mean conditions at any latitude and longitude as a function of the time of day, season, and solar activity level. Several generations of the IRI model have been used for forecasting of parameters of the ionized sphere of the Earth. However, in all its versions (including the recent one IRI 2000 [Bilitza, 2001]) the Bent and Llewellyn [1972] model of the electron density vertical profile in the topside ionosphere based on the data of the topside sounding on board the Alouette 1 and Alouette 2 satellites is used.
The comparison of IRI with the data of the satellite ionosonde on board Ionospheric Sounding Satellite (ISSb) showed that IRI considerably overestimates the electron concentration in the topside ionosphere (up to a factor of 5 at high latitudes and under high solar activity [Iwamoto et al., 2002]). A need to improve the IRI-Bent model is emphasized by the problems of fitting IRI to current plasmasphere models [Gallagher et al., 2000; Webb and Essex, 2000]. The authors of the latter models had to limit the ionospheric part of IRI by altitudes of 500-600 km to provide a continuous transition from the ionosphere to the plasmasphere, the plasmasphere models being developed independently of IRI. That is why many efforts are undertaken to improve IRI in the height region of the topside ionosphere and plasmasphere [Bilitza, 1985; Bilitza and Williamson, 2000; Bilitza et al., 1998; Gulyaeva, 2003; Gulyaeva et al., 2002; Rawer, 1990].
Current empirical models of the ionosphere (such as IRI, Russian Standard Model SMI [Chasovitin et al., 1998], and the European Commission on Science and Technology COSTProf model [Radicella and Leitinger, 2001]) use the expression for the electron profile shape via the hmF2 height and the maximum electron density NmF2. The profile shape below the ionization maximum is in the best way characterized by the half width of the bottomside ionosphere [Gulyaeva, 1983] used in the IRI and SMI models. The half width is defined as the difference of the heights ( hmF2 -h05 bot ), where the h05 bot height below the maximum corresponds to the electron density of 0.5 NmF2 and to a decrease of the maximum electron density in the ionosphere by a factor of 2, respectively, hmF2 being the height of the ionization maximum.
The half width of the topside ionosphere is defined similar as an increment of height from hmF2 to the h05 top level above the ionization maximum where the electron density is equal to 0.5 NmF2:
 | (1) |
The half-width parameter is proportional to the scale height of the topside ionosphere, H top, indicating the height interval for 1/e decay of electron concentration. For example, for the Chapman a layer [Chapman, 1931] the scale height is determined by
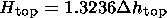 | (2) |
The formula of the Chapman a layer with a constant scale height above the ionization maximum is used for the extrapolation of the Ne(h) profile toward the topside ionosphere to produce the total electron content Ionosphere Total Electron Content (ITEC) from ionograms [Huang and Reinisch, 2001]. The empirical model of the half width of the topside ionosphere may be used to model the scale height (taking into account the proportionality of equation (2) of the two parameters) in various solar and geophysical conditions to increase the accuracy of ITEC calculations from the ground-based ionosonde network. Moreover, it makes it possible to improve considerably the IRI electron density profile shape of the topside ionosphere as described below.
The topside sounding data from the International Satellites for Ionospheric Studies, ISIS 1 (1969-1971, the orbit altitude was 500-3500 km), ISIS 2 (1971-1980, the orbit altitude was 1400 km) [Bilitza et al., 2003] and Intercosmos 19 satellite (1979-1982, the orbit altitude was 500-1000 km) are used as the database in the present study. These data cover more than a complete cycle of solar activity, including the whole range of diurnal, seasonal, and spatial variations in the vertical profile of the electron density Ne(h) above the F2 -layer maximum up to the satellite orbit. Most of these profiles do not include the F2 peak being terminated at the extreme observed plasma frequency f max. To compensate for that shortcoming, the lowest profile point has been extrapolated toward the F region peak with increment of frequency and height assumed so that the critical frequency foF2=1.05 f max and the peak height hmF2=h(f max) -30 km [Kishcha and Kochenova, 1996]. For further analysis more than 50,000 Ne(h) profiles under quiet geomagnetic conditions (index Kp<3 ) have been selected. The half width (1) was determined from the Ne(h) profile at Ne=0.5 NmF2. To create the empirical model mean values of the half width Dh top normalized to the hmF2 height were calculated:
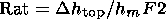 | (3) |
Ratio of equation (3) was determined for the specified ranges of spatial and
temporal variations under quiet magnetic conditions according to the
following scheme:
(1) four levels of solar activity averaged over 81 days (three solar
rotations) of sunspot number
Rz during the solar minimum
( 0
The choice of the three parameters indicated above is not incidental. It
corresponds to the driving parameters of the Bent's model: geomagnetic
latitude, solar radio emission flux
F10.7 at 10.7 cm
(proportional to the
sunspot number
Rz ), critical frequency
foF2, and the maximum height
hmF2, two latter parameters depend on local time.
Other
dependencies of the half width of the topside ionosphere on solar and
geophysical conditions are implied by variations of the
hmF2 parameter
of equation (3).
The results of the analysis of observations on board ISIS 1, ISIS 2, and
IK 19 provide an empirical model of the variations of half width in the
topside ionosphere normalized to the ionization peak height. It depends
on four driving parameters (sunspot number
Rz, absolute value of
geomagnetic latitude
|F|, local time LT, and the peak height
hmF2 ) and
contains 200 mesh point values which make it possible to apply a linear
interpolation of the ratio (3) for any intermediate solar and geophysical
conditions. Relevant FORTRAN subroutine TOPH05 providing
h05 top height is incorporated in ISO-IRI software (IRI version
for the
International Standardization Organization)
(available at ftp site of
IZMIRAN ftp://ftp.izmiran.rssi.ru/pub/izmiran/SPIM/).
Figure 1 shows that at all levels of solar activity an increase
of the ratio
of the half width to the ionization maximum height is observed within
the limits 0.3-0.8 from low to high geomagnetic latitudes. The
half-width values at the dawn hours are prevailing. These results allow us to
undertake a correction of the IRI model in the way described below.
The analytical description of the model of the topside ionosphere
vertical profile in IRI
[Bent and Llewellin, 1972;
Rawer et al., 1978]
for the altitudes
hmF2
We introduce a multiplier
q in equation (4):
where
The expressions for
X and
Y as well as all corresponding
coefficients
b,
d,
h, and
z are given by
Rawer at al. [1981]
as functions of
geomagnetic latitude, solar radio emission flux, and
F2 -layer critical
frequency.
Taking into account that
q = 1 for the initial IRI-Bent expression, we
obtain a correcting factor
q
As a result, the topside ionosphere vertical profile passes through an
additional correction point
Ne(h05 top) and its shape in the topside
ionosphere changes due to the allowance for the
q factor based on the
ISIS/IK 19 model. Relevant update of IRI subprograms for the topside
ionosphere profile with its extrapolation according to the SMI
plasmasphere model up to the plasmapause heights (up to 35,000 km) is
made included into the ISO-IRI software package in the project of the
standard of the ionosphere and plasmasphere of the Earth of the
International Organization on Standardization (ISO)
[Gulyaeva, 2003;
Gulyaeva et al., 2002].
The calculations by the SMI, IRI-Bent, and ISO-IRI (after the
correction of the topside ionosphere half width) were performed fitting
the parameters of the
F region peak ( NmF2 and
hmF2 ) from the
EISCAT observations. One can see that the SMI and improved ISO-IRI
models describe well the shape of the vertical profile in the topside
ionosphere. In all cases the initial IRI-Bent model gives overestimated
width of the plasma layer in the topside ionosphere as compared with
observations and other model calculations improved according to the
results of the ISO-IRI correction.
Using the data of the ionosondes on board the ISIS 1, ISIS 2, and IK 19
satellites, an empirical model of the topside ionosphere half width
Dh top normalized to the ionization
maximum height is created. The
model provides
Dh top dependence on local time,
geomagnetic latitude,
and solar activity for quiet geomagnetic conditions. The model provides
an additional point for specification of the electron density profile in the
International Reference Ionosphere Model. Its correction is realized in
the software of the ISO-IRI ionosphere-plasmasphere model proposed
as a standard of the International Standardization Organization (ISO).
The approbation of the modelling results, using the independent data of
EISCAT incoherent scatter and the GPS-TEC navigation satellite
signals, demonstrates the advantages of the proposed method as
compared with the initial IRI model. The calculations using the Russian
Standard Model give the results comparable to the ISIS 1, ISIS 2, and
IK 19 results.
Belehaki, A., and N. Jakowski, Studies of the ionospheric ionization over
Athens using ground ionosonde and GPS-derived TEC values,
Acta Geod.Geophys. Hung., 37 (2-3), 163,
2002.
Benkova, N. P., N. A. Kochenova, A. D. Legenka, M. N. Fatkullin,
and M. D. Fligel, Model representation of mid-latitudinal electron
density by means of Interkosmos 19 data,
Adv. Space Res., 4 (1), 51,
1984.
Bent, R. B., and S. K. Llewellyn, Documentation and description of the
Bent ionospheric model,
Rep. AFCRL-TR-73-0657, Air Force
Geophys. Lab., Hanscom AFB, Mass., 1972.
Bilitza, D., Electron density in the equatorial topside,
Adv. Space Res., 5 (10), 15,
1985.
Bilitza, D., International Reference Ionosphere 2000,
Radio Sci., 36 (2), 261,
2001.
Bilitza, D., and R. Williamson, Towards better representation of the IRI
topside based on ISIS and Alouette data,
Adv. Space Res., 25 (1), 149,
2000.
Bilitza, D., C. Koblinsky, R. Williamson, and S. Bhardwaj,
Improving the
topside electron density model for IRI,
Adv. Space Res., 22 (6), 777,
1998.
Bilitza, D., B. Reinisch, R. Benson, J. Grebowsky, N. Papitashvili,
X. Huang, W. Schar, and K. Hills,
Online data base of satellite sounder
and insitu measurements covering two solar cycles,
Adv. Space Res., 31 (3), 769,
2003.
Chapman, S.,
The absorption and dissociative or ionizing effect of
monochromatic radiation in the atmosphere on a rotating Earth,
Proc. Phys. Soc. London, 43, 26,
1931.
Comite Consultati International des
Radiocommunications
(CCIR),
Atlas of ionospheric characteristics, Rep. 340,
Geneva, 1986.
Chasovitin, Yu. K., T. L. Gulyaeva, M. G. Deminov, and S. E. Ivanova,
Russian Standard Model of the Ionosphere (SMI),
Proceedings of COST251 Workshop, Side, Turkey, COST 251 Tech. Doc. 5 TD(98)005,
p. 161,
Rutherford Appleton Lab.,
Oxford,
Chilton, UK,
1998.
Gallagher, D. L., P. D. Craven, and R. H. Comfort,
Global core plasma
model,
J. Geophys. Res., 105 (A8), 18,819,
2000.
Gulyaeva, T. L., Implementation of a new characteristic parameter into
the IRI sub-peak electron density profile,
Adv. Space Res., 2 (10),
191,
1983.
Gulyaeva, T. L., International standard model of the Earth's ionosphere
and plasmasphere,
Astron. Astrophys. Trans., 22 (4-5),
639, 2003.
Gulyaeva, T. L., X. Huang, and B. W. Reinisch,
Ionosphere-plasmasphere model software for ISO,
Acta Geod. Geophys. Hungarica, 37 (2-3), 143,
2002.
Huang, X., and B. W. Reinisch, Vertical electron content from
ionograms in real time,
Radio Sci., 36 (2), 335,
2001.
Iwamoto, I., H. Katoh, T. Maruyama, H. Minakoshi, S. Watari, and
K. Igarashi,
Latitudinal variations of solar flux dependence in the
topside plasma density: comparison between IRI model and
observations,
Adv. Space Res., 29 (6), 877,
2002.
Kishcha, P. V., and N. A. Kochenova,
Model for the height of the
ionosphere maximum in main ionospheric trough zone,
Geomagn. Aeron. (Engl. Transl.), 35 (6), 787,
1996.
Radicella, S. M., and R. Leitinger, The evolution of the DGR approach
to model electron density profiles,
Adv. Space Res., 27 (1), 35,
2001.
Rawer, K., Proposed improvements of the IRI topside profile formula.
Adv. Space Res., 10 (11), 75,
1990.
Rawer, K., D. Bilitza, S. Ramakrishnan, and N. Sheikh,
Intentions and
build-up of the International Reference Ionosphere,
in Operational Modelling of the Aerospace Propagation Environment, AGARD Conf.
Proc., 238,
6.1,
1978.
Rawer, K., J. V. Lincoln, and R. O. Conkright (Eds.),
International
Reference Ionosphere IRI 79,
Rep. UAG 82,
243 pp.,
WDC A for STP,
NOAA, Boulder, Colo.,
1981.
Stanislawska, I., G. Juchnikowski, Lj. R. Cander, L. Ciraolo,
P. A. Bradley, Z. Zbyszynski, and A. Swiatek, The kriging method
of TEC instantaneous mapping,
Adv. Space Res., 29 (6), 945,
2002.
Webb, P. A., and E. A. Essex,
An ionosphere-plasmasphere global
electron density model,
Phys. Chem. Earth, Part C, 25 (4), 301,
2000.
Figures 1a, 1b, 1c, and 1d show the half width of the topside ionosphere
normalized to the peak height value according to observations on board
the ISIS 1, ISIS 2, and IK 19 satellites and also the results of
calculations using the IRI and SMI models. The results for IRI differ
considerably from those for SMI and the data of ISIS and IK 19. In
particular, under high solar activity ( Rz=150 ) at high dip latitudes
(70-90o) the
h05 top height (where half decay of the peak electron density
occurs) goes outside the topside ionosphere in IRI (exceeds 1000 km)
and the ratio of equation (3) goes out of the frames of Figure 1a. The IRI
values for the half width are overestimated also at high solar activity
Rz=100 in the polar zone (Figure 1b). In the vicinity of the equator, IRI
also provides overestimated results as compared with the data of SMI,
ISIS, and IK 19, though the shortcomings of the Bent's model near the
equator were partly improved by
Bilitza [1985].
The SMI model
provides a better agreement of the relation (3) with the data of ISIS and
IK 19 than the IRI model, the fact being most evident at high latitudes
under high solar activity. This is explained by the use of the topside
ionosphere model by
Benkova et al. [1984]
in SMI based on the IK 19
data.

Figure 1
3. Correction of the Topside Ionosphere Model by the
Half-Width
Parameter
 h
h  1000 km
was presented by
Rawer et al. [1981]:
1000 km
was presented by
Rawer et al. [1981]:

(4) 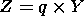
(5) 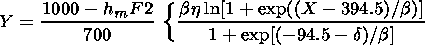
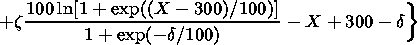
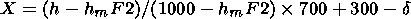
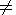 1 from equation (4) and (5), installing
Ne = 0.5 NmF2 and
h = h05 top determined from the empirical model based
on the ISIS and IK 19 data:
1 from equation (4) and (5), installing
Ne = 0.5 NmF2 and
h = h05 top determined from the empirical model based
on the ISIS and IK 19 data:
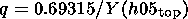
(6) 4. Approbation of the Corrected ISO-IRI Model
Figure 2 shows the comparison of three model calculations of
the
electron concentration
Ne(h) with the results of observations by the
European incoherent scatter facility EISCAT at Tromsö
(the geodetic
coordinates 69.6o N, 19.2o E, the geomagnetic latitude 66.9o
N)
in the
equinox period (6-7 September 1988) under high solar activity
( Rz=110 ) and quiet geomagnetic conditions.

Figure 2
Observations of the GPS navigational satellites from the orbit
of 20,000 km
to the Earth's surface provide the data on the total electron content
(TEC) useful for testing of ionosphere-plasmasphere models.
Figure 3
shows the diurnal behavior of the monthly median according
to the
GPS-TEC data at middle latitudes (Hailsham, 50.9o N, 0.3o E,
F = 53.4 o N; and Matera, 40.6o
N, 16.7o E,
F =40.3 o N)
for December
(Figure 3,
top) and June
(Figure 3,
bottom) 2002. Figure 3 shows also the medians of the
total electron content ITEC
[Huang and Reinisch, 2001]
derived from
the ionograms obtained in the nearest points of Fairford (51.7o N,
- 1.8 o E,
F = 54.6 o N) and San Vito
(40.7o N, 17.9o E,
F =40.5 o N). The
ITEC parameter is systematically lower than GPS-TEC because the
former includes the electron content up to a height of 1000 km without
taking into account the plasmasphere contribution seen in the
GPS-TEC
data
[Belehaki and Jakowski, 2002].
Model calculations of TEC were
performed for monthly mean conditions introducing median parameters
of the
F region maximum ( NmF2 and
hmF2 ) taken from ionosonde
observations. The comparison of the results of the TEC calculations
using SMI,
IRI-Bent, and ISO-IRI models shows that the correction of
the ISO-IRI model leads to a significant improve of the
IRI-Bent results
initially overestimated by a factor of up to 2 as compared with the
observations in winter conditions under high solar activity ( Rz=110 ).
The results of the TEC calculations using the SMI model overestimated
in both examples have lower accuracy than the results based on the
ISIS/IK 19 model.

Figure 3
The latitudinal variations in the total electron content TEC
in the
ionosphere and plasmasphere of the Earth according to the initial
IRI-Bent model, the ISO-IRI model corrected by the ISIS/IK 19 data, and
the SMI model are shown in Figure 4. They are compared with the
latitudinal variations in the observed values of the total electron content
in April 2002 at a latitude of 30o E derived from the interpolation maps
of the observed GPS-TEC data
[Stanislawska et al., 2002].
One can see
that the correction by the topside ionosphere parameter in the ISO-IRI
model improves considerably the results of the IRI-Bent model. Taking
into account that the
NmF2 and
hmF2 parameters were taken in this
case from the
CCIR [1986]
map
used in the IRI and SMI models, one
may state that a good agreement with observational data is achieved.

Figure 4
5. Conclusions
Acknowledgments
The ISIS data (Robert Benson, PI) and IRI source
code (Dieter Bilitza, PI) were processed and made available online from
NASA’s National Space Science Data Center
(ftp://nssdcftp.gsfc.nasa.gov/). The author thanks Bodo Reinisch and
Huang Xueqin for providing the prompt database of ISIS 1 and ISIS 2,
Kristian Shlegel for the EISCAT data, Ljiljana Cander for GPS-TEC
data, and Iwona Stanislawska for the numerical mapping of the GPS-TEC
data.
References
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on March 17, 2004.