Application of wavelet analysis to quasi-2-day oscillation occurrence in the time variations of f_oF2

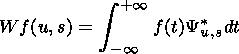
Elsa Mohino and Miguel Herraiz

Department of Geophysics and Meteorology, University Complutense of Madrid, Madrid, Spain

Edward Kazimirovsky

Institute of Solar-Terrestrial Physics, Irkutsk, Russia

Contents

Abstract

Introduction

The 2-day wave in the middle atmosphere is presumed to be forced from the lower atmosphere and could be the manifestation of both a global normal Rossby mode and a local unstable wave [e.g., Altadill et al., 1998, and references therein; Palo et al., 1999]. The quasi-2-day wave was found experimentally in the time variations of the mesosphere/lower thermosphere dynamics [e.g., Clark et al., 1994; Palo et al., 1999, and references therein].

A wide number of investigations concerning the "coupling from below" have considered these quasi-2-day oscillations in the upper ionosphere using different types of periodogram analysis [e.g., Apostolov et al., 1994, and references therein; Pancheva et al., 1994]. One of the rather new and efficient methods is the so-called wavelet analysis.

The purpose of the present research is to study the applicability of the wavelet analysis for the revelation of the possible quasi-2-day oscillations in the ionospheric parameter f_oF2.

By using the wavelet analysis the time-frequency variations of the time series can be measured, and the moment of occurrence of a certain type of oscillation can be more precisely placed in the time domain. The basic idea behind wavelet transform is to correlate the given time series ( f(t) ) with a size-variable wave packet ( Y_u,s ). The latter must fulfill certain requirements to provide a stable and complete representation of the given time series, therefore, to be used as a wavelet. The wavelet transform is given by Mallat [1998]:

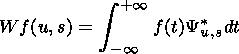(1)

where the asterisk accounts for the complex conjugate of the wavelet, u is the temporal displacement that locates the wavelet in the time series and s is the scale parameter. Parameters u and s are used, correspondingly, to move the wavelet through time and change its scale.

Figure 1

An example of wavelet is displayed in Figure 1. It is called the "Morlet wavelet,'' and it is given by equation:

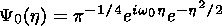(2)

By moving the wavelet through the time series (using parameter u ) and correlating each other, one can obtain information about when the time series behaves in a way similar to the wavelet, that is, when it shows a special feature round a certain frequency. To look for other frequency content, one changes not the shape of the wavelet but its scale(s):

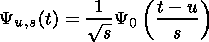(3)

Finally, information can be displayed in a two-dimensional contour: x axis contains the time domain and y axis contains the scale (frequency content). The bigger the scale (smaller frequency), the poorer the precision we have about when the oscillation took place.

Figure 2

An example of this wavelet transform is shown in Figure 2 where the normalized wavelet power spectrum ( |Wf(u,s)|²/s² ) is presented against time and period of oscillation (inverse of frequency). The cross-hatched regions indicate the "cone of influence'' where the edge effects become important and a decreasing of the wavelet power spectrum of the maxima located there may take place. The thick contour is the 90% confidence level for a corresponding red noise spectrum.

Software for wavelet analysis and red noise significance test provided by the Torrence and Compo wavelet analysis toolkit [Torrence and Compo, 1998] are used in this study to obtain quantitative results. The software is available through http://paos.colorado.edu/research/wavelets/.

2. Data and Analysis

Hourly values of f_oF2 for 1998 measured in the station of El Arenosillo (southwest Spain) (37.3^o N, 6.9^o W) and in El Ebro observatory (northeast Spain) (40.8^o N, 0.5^o E) are used to study the quasi-2-day oscillation. Missing values were linearly interpolated between the data corresponding to the preceding and following hours (provided the gap did not exceed two hours) or between the data of the preceding and following days at the same hour (for bigger gaps).

It is convenient to bear in mind the fact that the significance tests are meant to be used with a stationary time series. Nevertheless, our series clearly exhibit a nonstationary behavior. On the one hand, the variance of the time series varies from one month to another. So as to obviate this, we have divided the whole series in 12 parts that correspond to each month, reducing in this way the variance variability. In the quasi-2-day oscillation study, this methodology does not lead to a great loss of information near the edges of the month series because this period is still small compared with the approximately 30-day length. Nevertheless, it could turn out to be a problem when seeking higher periods of oscillation. On the other hand, our series exhibit a very important 24-hour period. In order to avoid it, we have worked with the hour anomaly by removing from each value the correspondent hourly mean. The hourly mean has been calculated using the data corresponding to five consecutive geomagnetic nonperturbed ( Ap<20 ) days.

The continuous wavelet transform is applied to the 24 normalized (dividing by each standard deviation) time series using the Morlet wavelet (equation (1)).The normalized wavelet power spectrum is represented in a contour plot against u and s, which can be transformed to time of occurrence and period (frequency) of oscillation.

Many geophysical time series show appreciable autocorrelation between successive measurements, what leads to a suppression of the power spectrum at high frequencies and a consequent inflation at lower ones, as compared to the power spectrum of white noise. This phenomenon has been called "red noise''. In this paper we have used the AR(1) process (first-order autoregressive process) as the red noise with which to compare our time series. This first-order linear Markov process is given by

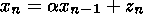(4)

where a is a constant ( |a|<1 ), z_n is a white noise process, x_n-1 is the immediately previous value in the time series, x_n=0, x_n²=s² (constant) and x_nx_n-k=0 with k 0 [Gilman et al., 1963]. For more details on the red noise significance test, interested readers are referred to Torrence and Compo [1998]. From this article we can define the scale-averaged wavelet power spectrum as the weighted sum of the wavelet power spectrum over scales s₁ and s₂ and taking into account the fact that we are working with a discrete time series:

(5)

The scales used in this study are those that correspond to averaging between the period of 38 and 54 hours.

Figure 3

Time series exhibit a very similar behavior in both stations throughout the whole year under study. Greater differences are found in summer time. This similarity is transferred to the wavelet power spectrum, though smaller periods display more differences. An example of this similarity can be seen by comparing Figure 3, which shows the normalized wavelet power spectrum for the month of December 1998 at El Ebro observatory, with Figure 2, corresponding to the same month but at El Arenosillo station.

Figure 4

Figure 5

The results of averaging between periods of 38 and 54 hours present, in general, great resemblance when comparing both stations: relative maxima are found to occur simultaneously, though their relative intensities may, in some cases, show some discrepancies. An example of a month that displayed great resemblance between stations can be found in Figure 4 (December 1998). Conversely, Figure 5 shows the month where more differences were found (July 1998).

For each station, the analysis found seven episodes of occurrence of oscillation in the periodic range under study (38 to 54 hours) that were significant over the 90% confidence level (dashed lines in Figures 4 and 5. Generally, these events were found simultaneously at both stations, though there were cases when a significant peak at one station was not significant at the other. An example of this kind of discrepancies may be observed in Figure 4: the second peak (centered around 20 January) is significant al El Ebro observatory, though not at El Arenosillo station.

In order to compare these results, the traditional periodogram analysis [Bloomfield, 1976; Stull, 1988] has been used, as it is one of the most commonly used techniques for the detection of the quasi-2-day oscillation [Altadill et al., 1998; Apostolov et al., 1994; Lastovicka, 1997]. This raises the question about what conditions should be fixed for this comparison. On the one hand, it could be desirable to use in the analysis the same variance, as this measure is used to establish the statistical significance of a certain peak. In this way it could be suitable to apply the periodogram analysis to each month. This would mean looking for 30 24/48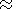 15 oscillations with the periodogram analysis. Nevertheless, on the other hand, it could be desirable to look for the same number of oscillations in the time series with both techniques. Using the Morlet wavelet with w₀=6 (see Figure 1), we are looking for six oscillations. In this way, it would be more convenient to use the periodogram analyis seeking the occurrence of approximately six cycles in order to detect the presence of a certain oscillation (quasi-2-days in our case). Finally, we have decided to compare both techniques in this last way, dividing the whole time series in segments with length of 320 hours (6 times 54 hours) and a time shift of 12 hours.

In contrast to the red noise test used in the wavelet analysis, the periodogram analysis has been found to be not as robust when applied to the hour anomaly: once the diurnal period has been removed, many periodic bands became significant. This is due to the fact that this methodology takes into account only the variability explained by each period against the total. By removal of the main source of variability (diurnal period), many periods become significant. This does not happen when using wavelet analysis and red noise significance test. To establish the statistical significance of a certain peak of the spectrum, not only the variance of the whole series but also the period are taken into account. Once compared, we concluded that the results derived from both techniques do not generally agree in the 38 to 54 hour periodic range.

One could wonder if a change in the periodic resolution of the wavelet analysis would alter the results. Up to now, we have been using the wavelet analysis with four samples per scale and, thus, using only three values (38.1, 45.3 and 53.8 hours) in the averaging of the periods ranging from 38 to 54 hours, while the periodogram analysis resolution used was of an hour. When changed to 32 samples per scale, corresponding to an averaging of 17 values for the periodic range under study, we have found no appreciable changes in the results.

Figure 6

One may expect to find considerable differences in the results of wavelet analysis if we demand more stability in the oscillation packets, that is, a bigger number of cycles. We have changed w₀ from 6 to 8 (we are now seeking the occurrence of eight cycles), and the results are qualitatively equal. Figure 6 shows the normalized wavelet power spectrum for the month of December at El Arenosillo station when using w₀=8. Comparing Figure 6 with Figure 2, one can observe that they are similar, the 90% significant levels over red noise are located over the same time and period.

Figure 7

Finally, where do these significant peaks found by the wavelet analysis in the periodic range between 38 and 54 hours come from? The origin of these peaks seems to be closely connected with the presence of abrupt changes in the geomagnetic activity that, in turn, would bring abrupt changes in the time series, to which the wavelet analysis has been found to be specially sensitive. The clearest example of this relationship can be observed in Figure 7 (August 1998, El Arenosillo). Nevertheless, it should be noted that there are two cases of significant peaks (7-8 June, both stations and 20 December at El Ebro observatory) for which no geomagnetic abrupt change has been found.

4. Conclusions

Wavelet analysis has been used for the detection of oscillations in the periodic range between 38 and 54 hours, and the results have been compared with the traditional periodogram analysis. The former appears to be a robust and adaptable tool, specially sensitive to compact wave packets, which were related, in general, with the presence of abrupt changes in geomagnetic activity, while the periodogram analysis seeks stability of the oscillation in the whole time window (320 hours in our case). From these results we can conclude that the wavelet analysis is not an adequate tool for seeking oscillations of quasi-2-days in f_oF2. These oscillations are very weak and introduce very little variability in the time series, so the wavelet analysis is not capable of distinguishing them from the red noise background. Investigators of the quasi-2-day oscillation in the ionospheric parameter f_oF2 should take into account our results when thinking of applying the wavelet analysis to their study, as we have shown that positive results of the wavelet analysis in the periodic range under study had a direct relation with abrupt changes in the geomagnetic activity. Nevertheless, this technique could be very useful applied to the detection of oscillation of shorter temporal duration in f_oF2 parameter, like TIDs.

Acknowledgments

References

Altadill, D., J. G. Solé, and E. M. Apostolov, First observation of quasi-2-day oscillations in ionospheric plasma frequency at fixed heights, Ann. Geophys., 16, 609, 1998.

Apostolov, E. M., L. Alberca, and D. Altadill, Solar cycle and seasonal behaviour of quasi-two-day and five-day oscillations in the time variations of f_oF2, Ann. Geofis., 37 (2), 187, 1994.

Bloomfield, P., Fourier Analysis of Time Series: An Introduction, John Wiley, Hoboken, N.J., 1976.

Clark, R. R., A. C. Current, A. H. Manson, C. E. Meek, S. K. Avery, S. E. Palo, and T. A. Aso, Hemispheric properties of the 2-d wave from Mesosphere-Lower Thermosphere radar observations, J. Atmos. Terr. Phys., 56, 1279, 1994.

Gilman, D. L., F. J. Fuglister, and J. M. Mitchel Jr., On the power spectrum of "red noise", J. Atmos. Sci., 20, 182, 1963.

Lastovicka, J., Observation of tides and planetary waves in the atmosphere-ionosphere system, Adv. Space Res., 20 (6), 1209, 1997.

Mallat, S., A Wavelet Tour of Signal Processing, Academic Press, San Diego, Calif., 1998.

Palo, S., R. G. Roble, and M. E. Hagan, Middle atmosphere effects of the quasi-two-day wave determined from a General Circulation Model, Earth Planets Space, 51 (7,8), 629, 1999.

Pancheva, D., L. Alberca, and B. de la Morena, Simultaneous observations of quasi-two-day variations in the lower and upper ionosphere over Europe, J. Atmos. Terr. Phys., 56, 43, 1994.

Stull, R. B., An Introduction to Layer Boundary Meteorology, Kluwer Acad., Norwell, Mass., 1988.

Torrence, C., and G. P. Compo, A practical guide to wavelet analysis, Bull. Am. Meteorol. Soc., 79 (1), 61, 1998.