Relation of the Dst index to solar wind parameters

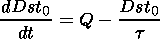
Yu. P. Maltsev and B. V. Rezhenov

Polar Geophysical Institute, Apatity, Russia

Contents

Abstract

1. Introduction

The major manifestation of a magnetic storm is the global decrease (depression) of the geomagnetic field. The quantitative measure of this perturbation is the Dst index, which is determined as the H component disturbance at low-latitude observatories averaged over longitudes. The temporal behavior of the Dst index corrected for the solar wind dynamic pressure is commonly described by the following equation [Feldstein, 1992; Gonzalez et al., 1994]

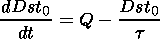(1)

where Q is the so-called coupling function, t is the decay time of the electric currents responsible for the storm-time geomagnetic field depression. The problem of contribution of different solar wind parameters to the function Q has not been finally solved yet. The majority of the investigators relate it mainly to the interplanetary electric field E_y = -VB_z [Burton et al., 1975; Feldstein et al., 1984; Grafe, 1988; Murayama, 1982; O'Brien and McPherron, 2000; Pisarsky et al., 1989; Pudovkin et al., 1985, 1988; Valdivia et al., 1996] where V is the solar wind velocity, B_z is the IMF vertical component in the GSM coordinate system. In particular, O'Brien and McPherron [[2000] obtained the following empirical expression

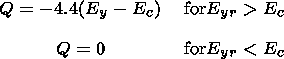(2)

Here E_c = 0.49 mV m ^-1, E_yr = -VB_s is the "refined" electric field component directed duskward, B_s is the IMF southward component. Some investigators report that the coupling function Q depends not only on E_y but also on the proton density [Murayama, 1982] and velocity [Pisarsky et al., 1989]. Another expression for Q was suggested by Perreault and Akasofu [1978]

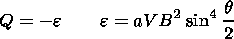(3)

Here a is a constant, B = (B_x² + B_y² + B_z²)^1/2 is the IMF modulus, q = arctan (B_y/B_z), B_y is the dawn-to-dusk IMF component. The parameter e is commonly called the Akasofu parameter.

Expressions (2) and (3) have some similarity -- they both show that the magnetosphere behaves as a half-wave rectifier: the IMF southward component affects it considerably stronger than the northward component does. The main difference is that (3) presumes dependence on two other IMF components (on B_x and B_y, with a smaller weight, though), whereas these components are absent in (2).

For decades an opinion existed that substorms contribute to the coupling function Q. However, Iyemori and Rao [1996] have shown convincingly that substorms rather weaken slightly the storm time depression than enhance it.

The characteristic relaxation time t of the magnetospheric currents responsible for the geomagnetic depression is of the order of 10 hr and varies in the course of a storm [Feldstein, 1992; Gonzalez et al., 1994]. It is not quite clear what factors affect this quantity. For instance, Valdivia et al. [1996] assume t = 12.5/(1 - 0.0012 Dst₀) hr whereas O'Brien and McPherron [[2000] found t = 2.40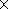 exp[9.74/(4.69+ E_yr) ] hr.

In this paper we examine the influence of various parameters on the coupling function Q and characteristic time t. Studying storm activity's relation to the solar wind parameters is complicated by the intercorrelation of the parameters themselves. One purpose of this paper is the analysis of the relation between different solar wind parameters. In order to exclude the effect of the intercorrelation of the parameters we shall try to examine the response of the Dst₀ to each parameter separately, that is, under the other parameters being kept constant.

2. Experimental Data

We used the OMNI database, which includes hourly values of all IMF components, velocity, and concentration of the solar wind protons as well as hourly Dst indices for 28 years, from 1963 to 1990. A total of 112,000 hourly data were used. The Dst index was corrected according to the following equation [Maltsev and Rezhenov, 2002]

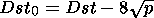(4)

where p = m n V² is the solar wind proton dynamic pressure expressed in nPa, m is the proton mass, V is the solar wind velocity, and n is the proton concentration. The derivative d Dst₀/dt was replaced by the ratio DDst₀/ Dt where Dt = 1 hr and DDst₀ is the difference between the values of Dst₀ for two successive hours.

3. Results

3.1. Dependence of DDst₀/Dt on Dst₀ and on Solar Wind Parameters

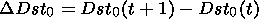Figure 1

Figure 1 shows the DDst₀ versus the vertical B_z and horizontal (B_x² + B_y²)^1/2 IMF components for the solar wind velocity in the range of 400 < V < 500 km s ^-1. The dependence is given for several ranges of Dst₀. The effect of the horizontal IMF component was analyzed under the northward B_z IMF. One can see that the southward IMF component (B_z < 0) affects DDst₀/ Dt more than the northward component IMF (B_z > 0). There is no dependence of Dst₀ on the horizontal IMF component.

Figure 2

Figure 2 shows the DDst₀ versus Dst₀ at 400 < V < 500 km s ^-1 for several ranges of the B_z IMF. The dependence has a form of almost straight lines, their slope depending on B_z IMF. Thus, according to formula (1), the characteristic time t depends on B_z IMF and does not depend on Dst₀.

Figure 3

Figure 3 shows the DDst₀ versus the solar wind velocity under the northward (left panel) and southward (right panel) orientation of the IMF. In both cases the dependence is almost linear. The slope of the curves is greater under the southward IMF. The right-hand side of Figure 3 together with the left-hand side of Figure 1 suggest that DDst₀ depends nearly linearly on the product -VB_s, that is, on the duskward electric field. The left-hand side of Figure 3 reveals a weak dependence of DDst₀ on the velocity under the northward IMF.

Figures 1-3 were drawn for all values of the solar wind density. The dependence of DDst₀ on the density is shown in Figure 4 for 400 < V < 500 km s ^-1 under the northward (left panel) and southward (right panel) orientation of the IMF in several ranges of Dst₀. One can see that there is no pronounced dependence of the Dst₀ on the proton density.

Figure 4

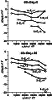
Figure 5

Figure 6

It is interesting to compare the relative effect of the electric field and Akasofu parameter on DDst₀. We have looked for the dependence of DDst₀ on each of these parameters under the condition that the other parameter was kept fixed. The result is shown in Figures 5 and 6. While calculating the Akasofu parameter according to formula (3), we assumed a = 1. The comparison of Figures 5 and 6 shows that the Akasofu parameter is considerably less geoefficient (its influence on DDst₀ is weaker) than the duskward electric field.

The curves shown in Figures 1 and 2 allow us to find approximation formulas for Q and t. First we averaged DDst₀ in bins with a size of 20 nT in Dst₀, 3 nT in B_z IMF, and 100 km s ^-1 in V. Then we found by the least square method the following formulae:

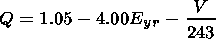(5)

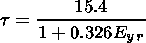(6)

3.2. Interrelation of the Solar Wind Parameters

Figure 7

Figure 7 demonstrates some statistical relations between the following solar wind parameters: n, V, B_z, B _horiz, |B|, E_yr, and e. One can see that the relations e (E_yr ), e (B_z), B _horiz (B_z), n(B_z), n(V) are strong; relations e (E_yr ), e (B_z), B _horiz (B_z), n(B_z), n(V) are moderate; and relations V(B_z), V(|B|), |B|(V) are weak.

3.3. Correlation Between Dst and Solar Wind Parameters

Figure 8

Figure 8 shows the dependence of Dst and Dst₀ on three IMF components, on the solar wind velocity and density, and on the e parameter. The strongest dependence is on the IMF southward component, velocity, and e parameter. The strengthening of the storm activity with the growth of the northward IMF as well as with the increase of B_x and B_y components seems unexpected. But taking into account the mutual correlation of the solar wind parameters, we can infer that it is just manifestation of the growing velocity and southward IMF. Both latter facts are a result of the solar wind velocity increase. Indeed, the dependence of Dst on B_x and B_y almost disappears once we introduce the restrictions 400 < V < 500 km s ^-1 and B_z > 0.

4. Discussion

Our formulae (5) and (6) do not differ strongly from expression (2) and the formula for t by O'Brien and McPherron [[2000], who suggested that the coupling function Q depends on the duskward interplanetary electric field only. We added the linear term for the solar wind velocity into the expression for Q. The dependence on V was found by Pisarsky et al. [1989] but with the coefficients strongly different from ours in expression (5). Our Figure 4 does not confirm the dependence of Q on the solar wind proton density obtained by Murayama [1982]. While calculating the characteristic time t we looked over many kinds of dependencies including t (Dst₀), suggested by Valdivia et al. [1996]. The dependence t( E_yr ) provides the best fit. One can see this fact directly in Figure 2.

As one can see from Figures 5 and 6, the Akasofu parameter e is less related to DDst₀ than the electric field E_yr. Analyzing a number of storm events, Feldstein [1992] and Murayama [1982] have found earlier that the behavior of DDst₀/ Dt is better described by the coupling function Q dependent on E_yr rather than on e. A similar result was obtained by Wu and Lundstedt [1997] with the help of the neural network technique. The good relation between Q and e found by Perreault and Akasofu [1978], Akasofu [1981, 1996], and Gonzalez et al. [1989] can be explained by the strong statistical correlation between e and E_yr.

Formulas (1) and (5) are important not only for a prediction of Dst₀ but also for distinguishing between the two existing theories of magnetic storms. The traditional theory regards the geomagnetic storm time depression as the ring-current effect. The ground magnetic disturbance produced by the ring current is proportional to the total energy content of magnetically trapped particles [Dessler and Parker, 1959; Sckopke, 1966]. The parameter e satisfies this concept perfectly because it is proportional to the solar wind magnetic energy flow. However, till now there have been no theoretical studies explaining quantitatively the observed dependence of Q on e (or on E_yr ) under the ring current concept. Moreover, by 2000 the Dessler-Parker-Sckopke relationship had been experimentally tested only in a few case studies. The first statistical study was performed by Greenspan and Hamilton [[2000], who analyzed 40 storms and did not find any correlation between the total particle energy content in the dayside and Dst index.

A new theory of magnetic storms suggested by Maltsev [1991] relates the storm-time depression to an increase of the magnetic flux in the magnetotail lobes. The magnetotail flux grows during storms due to the magnetic flux transport from the dayside to the tail as a result of the terrestrial magnetic field reconnection with the IMF southward component. The rate of this process does not depend on the solar wind energy flux. It depends on the duskward interplanetary electric field [Maltsev et al., 1996]. On the basis of this theory, Arykov and Maltsev [1996] calculated the coupling function Q(E_yr ), which is in quantitative agreement with the empirical expression obtained by Burton et al. [1975]. The latter does not differ much from (2) and (5). Maltsev and Ostapenko [[2002] processed a large database containing 20-year measurements of 11 satellites and found that the observed variation of the magnetotail magnetic flux is capable of contributing as much as 80% to Dst. Alexeev et al. [1996, 2001] also report on a large contribution of the magnetotail current to the storm-time depression.

5. Conclusions

We analyzed the hourly Dst and solar wind parameters for the 28-year period (112,000 data) and found that the solar wind coupling function Q in equation (1) can be presented as a linear combination of the duskward electric field E_yr (this term dominates) and velocity. The dependence on B_x and B_y IMF as well as on the solar wind density is negligible. The dependence on the Akasofu parameter e appeared to be weak if one examines it under nearly constant E_yr, whereas the dependence on E_yr remains strong and almost invariable when e is restricted by a narrow range. Thus, one can conclude that the storm activity is controlled by the magnetic flux transport from the dayside to the magnetotail rather than by the solar wind magnetic energy flow.

The value of Dst itself reveals a significant statistical correlation with the solar wind velocity and all IMF components. The relation of Dst to B_x, B_y, and e seems to be caused by intercorrelation of the majority of the solar wind parameters.

Acknowledgments

References

Alexeev, I. I., E. S. Belenkaya, V. V. Kalegaev, Ya. I. Feldstein, and A. Grafe, Magnetic storms and magnetotail currents, Journal of Geophysical Research, 101, 7737, 1996.

Alexeev, I. I., V. V. Kalegaev, E. S. Belenkaya, S. Y. Bobrovnikov, Ya. I. Feldstein, and L. I. Gromova, Dynamic model of the magnetosphere: Case study for January 9-12, 1977, Journal of Geophysical Research, 106, 25,683, 2001.

Akasofu, S.-I., Energy coupling between the solar wind and the magnetosphere, Space Sci. Rev., 28, 121, 1981.

Akasofu, S.-I., Search for the "unknown" quantity in the solar wind: A personal account, Journal of Geophysical Research, 101, 10,531, 1996.

Arykov, A. A., and Yu. P. Maltsev, Direct-driven mechanism for geomagnetic storms, Journal of Geophysical Research, 23, 1689, 1996.

Burton, R. K., R. L. McPherron, and C. T. Russell, An empirical relationship between interplanetary conditions and Dst, Journal of Geophysical Research, 80, 4204, 1975.

Dessler, A. J., and E. N. Parker, Hydromagnetic theory of geomagnetic storms, Journal of Geophysical Research, 64, 2239, 1959.

Feldstein, Ya. I., Modelling of the magnetic field of magnetospheric ring current as a function of interplanetary parameters, Space Sci. Rev., 59, 83, 1992.

Feldstein, Ya. I., V. Y. Pisarsky, N. M. Rudneva, and A. Grafe, Ring current simulation in connection with interplanetary space conditions, Planet. Space Sci., 32, 975, 1984.

Gonzalez, W. D., B. T. Tsurutani, A. L. C. Gonzalez, E. J. Smith, F. Tang, and S.-I. Akasofu, Solar wind-magnetosphere coupling during intense magnetic storms (1978-1979), Journal of Geophysical Research, 94, 8835, 1989.

Gonzalez, W. D., J. A. Joselyn, Y. Kamide, H. W. Kroehl, G. Rostoker, B. T. Tsurutani, and V. M. Vasyliunas, What is a geomagnetic storm? Journal of Geophysical Research, 99, 5771, 1994.

Grafe, A., The influence of the recovery phase injection on the decay of the ring current, Planet. Space Sci., 36, 765, 1988.

Greenspan, M. E., and D. C. Hamilton, A test of the Dessler-Parker-Sckopke relation during magnetic storms, Journal of Geophysical Research, 105, 5419, 2000.

Iyemori, T., and D. R. K. Rao, Decay of the Dst field of geomagnetic disturbance after substorm onset and its implication to storm-substorm relation, Ann. Geophys., 14, 608, 1996.

Maltsev, Yu. P., Relation of Dst variation to magnetospheric geometry, Geomagn. Aeron. (in Russian), 31 (3), 567, 1991.

Maltsev, Yu. P., and B. V. Rezhenov, Statistical study of the response of Dst index to the change of the solar wind dynamic pressure, Geomagn. Aeron. (in Russian), 42 (2), 175, 2002.

Maltsev, Yu. P., and A. A. Ostapenko, Comments on "Evaluation of the tail current contribution to Dst " by N. E. Turner et al., Journal of Geophysical Research, 107 (A1), 2002.

Maltsev, Yu. P., A. A. Arykov, E. G. Belova, B. B. Gvozdevsky, and V. V. Safargaleev, Magnetic flux redistribution in the storm time magnetosphere, Journal of Geophysical Research, 101, 7697, 1996.

Murayama, T., Coupling function between solar wind parameters and geomagnetic indices, Rev. Geophys. Space Phys., 20, 623, 1982.

O'Brien, T. P., and R. L. McPherron, An empirical phase space analysis of ring current dynamics: Solar wind control of injection and decay, Journal of Geophysical Research, 105, 7707, 2000.

Perreault, P., and S.-I. Akasofu, A study of geomagnetic storms, Geophys. J. R. Astron. Soc., 54, 547, 1978.

Pisarsky, V. Yu., Ya. A. Feldstein, N. M. Rudenova, and A. Prigancova, Ring current and interplanetary medium parameters, Studia Geophys. Geod., 33, 61, 1989.

Pudovkin, M. I., S. A. Zaitseva, and L. Z. Sizova, Growth rate and decay of magnetospheric ring current, Planet. Space Sci., 33, 1097, 1985.

Pudovkin, M. I., A. Grafe, S. A. Zaitseva, L. Z. Sizova, and A. V. Usmanov, Calculating the Dst -variation field on the basis of solar wind parameters, Gerlands Beitr. Geophysik, 97, 525, 1988.

Sckopke, N., A general relation between the energy of trapped particles and the disturbance field near the Earth, Journal of Geophysical Research, 71, 3125, 1966.

Valdivia, J. A., A. S. Sharma, and K. Papadopoulos, Prediction of magnetic storms by nonlinear models, Geophysical Research Letters, 23, 2899, 1996.

Wu, J.-G., and H. Lundstedt, Geomagnetic storm predictions from solar wind data with the use of dynamic neural networks, Journal of Geophysical Research, 102, 14,225, 1997.