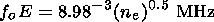
G. V. Givishvili and L. N. Leshchenko
Institute of Terrestrial Magnetism, Ionosphere, and Radio Wave Propagation, Troitsk, Russia
Givishvili and Leshchenko [[2001] were the first to try to reveal seasonal features of the temperature long-term trends at the height of the E -layer maximum hmE on the basis of the electron concentration and/or the critical frequency foE measurements. However, the annual variations of the molecular oxygen concentration [O2], the principal ionized constituent at E -layer heights, have been taken into account by Givishvili and Leshchenko [[2001] only indirectly, using the concentration ratio of the atomic oxygen O and molecular nitrogen N 2. The aim of this study is to consider more accurately factors determining the seasonal behavior of the electron production and loss rates in order to be able to analyze the fine structure of the seasonal variations of the long-term trends in the lower thermosphere temperature derived from ne or foE measurements.
The critical frequency foE is related to ne by
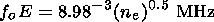 | (1) |
The equilibrium electron concentration ne in the E region only slightly depends on diffusion processes, thermospheric winds, and electric fields. Therefore the formulae is correct there:
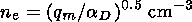 | (2) |
where qm is the ionization rate in the layer maximum and aD is the effective recombination coefficient. The values of qm and aD both depend on T. This fact makes it possible to determine reliably values of T at the height of the E -layer maximum hmE using the measurements of foE if the qm and aD dependencies on T are known.
The ionization of the E region is provided mainly by the solar radiation in the l = 97.7 nm and (Lyman- b ) 102.6 nm lines interacting with oxygen molecules. This two channels provide formation of 75-85% of all charged particles. An additional source of ion formation at heights of 100-120 km is related to the solar X rays interacting with oxygen molecules and also nitrogen molecules and oxygen atoms. Thus about 80-90% of the ionization rate q depend on the O2 content in the lower thermosphere. Therefore q is determined by the Chapman equation [Chapman, 1931]:
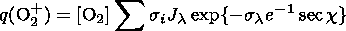 | (3) |
where
si and
sl
are the cross sections of
ionization and absorption for an O2 molecule, respectively,
c is the solar zenith angle,
Jl is the radiation flux at
the
wavelengths 102.6, 97.7, and 1-8 nm. The photoionization
cross-sections are
10-18,
2.5 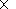 10-18,
and
(0.2-3.6)
10-18,
and
(0.2-3.6)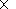 10-18 for 102.6 nm,
97.7 nm, and 1-8 nm,
respectively. The absorption
cross-sections are
1.5
10-18 for 102.6 nm,
97.7 nm, and 1-8 nm,
respectively. The absorption
cross-sections are
1.5 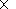 10-18,
4.0
10-18,
4.0 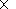 10-18,
and
(0.2-0.9)
10-18,
and
(0.2-0.9) 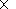 10-18 for the same wavelengths,
respectively
[Samson and Cairns, 1964;
Watanabe and Hinteregger, 1962].
All
sl
and
si are constant and do not influence
seasonal and long-term changes of the ionization rate. Therefore,
to simplify the process of
q (O2 ) calculations, we accept below
generalized values
si = 1.82
10-18 for the same wavelengths,
respectively
[Samson and Cairns, 1964;
Watanabe and Hinteregger, 1962].
All
sl
and
si are constant and do not influence
seasonal and long-term changes of the ionization rate. Therefore,
to simplify the process of
q (O2 ) calculations, we accept below
generalized values
si = 1.82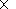 10-18 cm
2 and
sl
= 2.34
10-18 cm
2 and
sl
= 2.34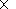 10-18 cm
2 taking into account the
weighted input of the above-indicated solar radiation ranges into
the ionization rate.
10-18 cm
2 taking into account the
weighted input of the above-indicated solar radiation ranges into
the ionization rate.
In the layer maximum where the dq( O2+)/dh = 0 condition [Chapman, 1931] is fulfilled we have
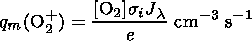 | (4) |
Equation (4) is not convenient for calculations of T because of two reasons. First, one has to have all the information on absolute values and seasonal variations of [O2]. However different authors [Alcayde et al., 1974; Mayr et al., 1976; Scialmon, 1974] give significantly different information. Second, to know the seasonal variations of the height where the dq(O2+)/dh = 0 condition is fulfilled, that is, to which height the derived temperature corresponds, one has to perform additional calculations to reconstruct the q(h) vertical profile using formula (3).
So we rewrite formula (3) in the form
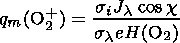 | (5) |
Here H( O2) = kT/mg is the scale height for O2, k is the Boltzmann constant, m is the molecular weight of O2, and g is the gravity acceleration. Substituting numerical values of k, m, g, s1, and s2 into formula (5), we obtain
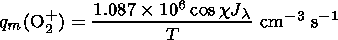 | (6) |
Now there is no need to know the absolute values of [O2]. According to Ivanov-Kholodny and Firsov [1974] the flux of the radiation ionizing O2 is
 |
where F10.7 is the solar activity index.
The loss of free electrons in the daytime quiet E region occurs in their dissociative recombination with NO+ and O2+ ions with the rate constants [Mehr and Biondi, 1969]:
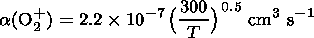 | (7) |
and
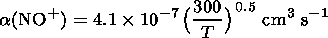 | (8) |
Since at the considered heights
ne = [ NO+] + [ O2+] and
a ( NO+) 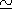 2a ( O2+),
the total loss rate is determined by
2a ( O2+),
the total loss rate is determined by
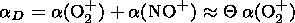 | (9) |
where
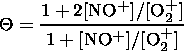 |
Finally, we have
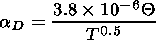 | (10) |
Two ways to calculate the temperature from the foE data are considered. In the first, formula (4) is taken into account, the second is based on formula (6). Substituting these two formulae and formulae (1) and (10) into equation (2), we have
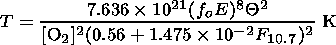 | (11) |
and
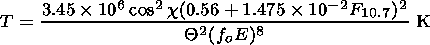 | (12) |
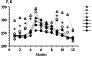
|
| Figure 1 |

|
| Figure 2 |
To specify the character of the seasonal variations of qm and hmE and also to estimate the influence of the seasonal variations of the Q parameter on the temperature evaluation, we use formula (12). Following IRI we presume that hmE = 110 km all over the year. The results of the calculations for the four stations indicated above are shown in Figure 1 as T(12) values. One can see that in this case the deviations between T(12) and T( M) are relatively small in summer but are considerable in equinox periods. The important thing is that a semiannual component which is absent in the annual variations of T( M) is visually seen in the seasonal behavior of T(12).
|
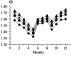
| Figure 3 |
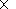 107 cm-3 in summer
[Gravens and Stewart, 1978].
At the same time,
the seasonal behavior of the molecular oxygen concentration
controlling the concentration of O+2 ions at heights of the
E region is also rather monotonous. This concentration decreases from
winter months to summer. Thus, there is no semiannual component in
the annual behavior of the [NO+]/[ O+2]
ratio and this ratio
should be higher in summer than in winter. Therefore it is not
clear what causes the seasonal variations of
Q presented in
the IRI model. There is only one source of data on the
E -layer ion
composition: the data of rocket mass-spectrometer measurements.
Evidently, there are not enough of these data to derive statistically
significant conclusions on the seasonal variability of the
[ NO+]/[ O+2] ratio.
107 cm-3 in summer
[Gravens and Stewart, 1978].
At the same time,
the seasonal behavior of the molecular oxygen concentration
controlling the concentration of O+2 ions at heights of the
E region is also rather monotonous. This concentration decreases from
winter months to summer. Thus, there is no semiannual component in
the annual behavior of the [NO+]/[ O+2]
ratio and this ratio
should be higher in summer than in winter. Therefore it is not
clear what causes the seasonal variations of
Q presented in
the IRI model. There is only one source of data on the
E -layer ion
composition: the data of rocket mass-spectrometer measurements.
Evidently, there are not enough of these data to derive statistically
significant conclusions on the seasonal variability of the
[ NO+]/[ O+2] ratio.
|
| Figure 4 |
Givishvili and Leshchenko [[2001] introduced into formula (12) a parameter g which took into account the [O2] seasonal variations according to the data of the rocket measurements of the [O]/[N2] ratio at a height of 130 km [Antonova and Katyushina, 1976]. In other words, T was calculated using
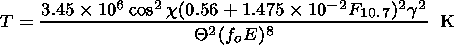 | (13) |
The evaluation of g from the data on the [O]/[N2] ratio made it possible to estimate the annual T variations at hmE rather approximately. More explicit description of the relative seasonal variations of [O2] at height of the E -layer maximum provides the MSIS model, if one determines the g parameter in another way: as a ratio g = [ O2]i/[ O2]J, where J stands for January and i = 1-12 corresponds to the month number. Thus g is characterized by the relative changes of [O2] at about 110 km relative the values in January.
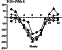
|
| Figure 5 |
One can easily see that the discrepancy between T(13) and the model values of the temperature T( M) is in this case maximum in summer months when the discrepancy reaches 100-200 K. In winter months the difference between T(13) and T( M) is small. This indicates to the fact that in winter hmE is actually close to 110 km. In summer months it should decent down to the altitudes where [O2] is considerably higher than at 110 km, as has been suggested earlier. This conclusion agrees with empirical models of the midlatitude ionosphere [Fatkullin et al., 1981; Givishvili and Fligel', 1971; Robinson, 1960]. According to these models the noon values of hmE vary during the year from the maximum winter values equal to 108-112 km to the minimum summer values of about 104-108 km. The incoherent scatter measurements conducted in Kharkov (50o N) in 1978-1983 also indicate to a lowering of hmE from winter to summer [Ivanov-Kholodny et al., 1998]. To check the conclusion on variability of the hmE and to estimate its changes during the year, we calculated g ( M)
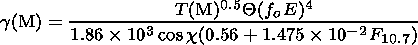 | (14) |

|
| Figure 6 |

|
| Figure 7 |

|
| Figure 8 |
Thus, we have now all the necessary information for calculation of the temperature at the heights of the E -layer maximum on the basis of the data on foE, including the data on the changes of both this very height (the hm( M) parameter) and the O2 concentration at this height, i.e., the gm( M) parameter.
As for the IRI model, it is worth mentioning that the reliability of the data on the electron concentration (frequency foE ) in it arises no doubts. Evidently, the same is not true for the seasonal variations of both the maximum height and ion composition of the E layer. The calculations performed show that the hmE height should vary over the year. However, the assumption on the absence of annual variations of the [NO+] and [O2+] generally speaking may not correspond to the reality. Nevertheless, some corrections to the accepted here algorithms of temperature calculations would be reasonable to insert only after statistically reliable data on the parameter Q seasonal behavior are obtained.
The analysis presented above makes in possible to make the following conclusions:
1. The method to evaluate the lower thermosphere temperature from the ionospheric vertical sounding data is specified. A parameter g is introduced which takes into account the seasonal variations of the O2 concentration at altitudes of the E -layer maximum. This parameter makes it possible to reproduce the annual variation of the lower thermosphere temperature at middle latitudes ( j = 42o-62 o N) on the basis of the critical frequency foE measurements.
2. The assumption on the constancy of the E -layer maximum height made in the IRI model, does not fit the reality. There is ground to believe that hmE = 110 km only in winter. During the rest of the year it is slightly lower. The amplitude of the seasonal variations of hmE depends on latitude, increasing from 1.6 to 4.3 km in the latitudinal band 42o-62o N.
3. The data on the seasonal variations of the ion composition at E -layer heights presented in the IRI are doubtful. To specify the character of the annual behavior of the [NO+]/[O2+] ratio, additional experimental studies are needed.
Alcayde, D., P. Bauer, and J. Fontanari, Long-term variation of thermospheric temperature and composition, J. Geophys. Res., 79 (4), 629, 1974.
Antonova, L. A., and V. V. Katyushina, Possible mechanism of formation of the semiannual density variations in the upper atmosphere, Geomagn. Aeron. (in Russian), 16 (2), 311, 1976.
Bilitza, D., International Reference Ionosphere--Status 1995/96, Adv. Space Res., 20 (9), 1751, 1997.
Chapman, S., The absorption and dissociatival or ionizing effect of monochromatic radiation in atmosphere on a rotating Earth, Proc. Phys. Soc., 43 (26), 483, 1931.
Fatkullin, M. N., et al., Empirical Models of the Midlatitude Ionosphere (in Russian), Nauka, Moscow, 1981.
Givishvili, G. V., and M. D. Fligel', On variations of the electron concentration in the E layer, Geomagn. Aeron. (in Russian), 11 (6), 984, 1971.
Givishvili, G. V., and L. N. Leshchenko, Seasonal trends in the temperature of the midlatitude lower thermosphere, Dokl. Akad. Nauk (in Russian), 376 (1), 97, 2001.
Gravens, T. E., and A. I. Stewart, Global morphology of nitric oxide in the lower E region, J. Geophys. Res., 83 (A6), 2453, 1978.
Hedin, A. E., Extension of the MSIS thermospheric model into the middle and lower atmosphere, J. Geophys. Res., 96, 1159, 1991.
Ivanov-Kholodny, G. S., and V. V. Firsov, Spectrum of solar short-wave radiation at various activity levers, Geomagn. Aeron. (in Russian), 14 (4), 674, 1974.
Ivanov-Kholodny, G. S., P. V. Kishcha, and T. G. Zhivolup, The base of the empirical model of the E -layer maximum height at middle latitudes, Geomagn. Aeron. (in Russian), 38 (5), 174, 1998.
Mayr, H. G., et al., Diurnal and seasonal variations in atomic and molecular oxygen inferred from atmosphere Explorer-C, Geophys. Res. Lett., 3 (2), 77, 1976.
Mehr, R., and M. A. Biondi, Electron temperature dependence and recombination of the O+2 and NO+ ions with electron, Phys. Rev., 181 (1), 264, 1969.
Robinson, B. J., Diurnal variation of the electron distribution in the ionospheric E layer, J. Atmos. Terr. Phys., 18 (2/3), 215, 1960.
Samson, J. A., and R. B. Cairns, Absorption and photoionization cross-sections of O2 and N 2 at intense solar emission lines, J. Geophys. Res., 69, 4583, 1964.
Scialmon, G., Neutral composition in the lower thermosphere, Radio Sci., 9 (2), 253, 1974.
Watanabe, K., and H. E. Hinteregger, Photoionization rates in E and F regions of the ionosphere, J. Geophys. Res., 67, 999, 1962.