Localized nonlinear electrostatic structures in the magnetosphere

A. V. Volosevich and F. M. Trukhachev

Physical Department, Mogilev State University, Mogilev, Belarus

Yu. I. Galperin

Space Research Institute, Moscow, Russia

Contents

Abstract

1. Introduction

Measurements with high time/space resolution made from rockets and satellites S3 3, Viking, Freja, Geotail, Interball 2, and most detailed from the FAST satellite, have revealed various types of moving electrostatic small-scale structures of plasma density and electric field in the regions of downward and upward field-aligned currents in the auroral magnetosphere (see reviews by Koskinen and Malkki [1993], and Lakhina et al. [[2000] and recent results, for example, of Ergun [1998a, 1998b]). Much theoretical work and numerical modeling was done to describe the formation of these structures [see, e.g., Berthomer et al., 1998; Das et al., 1998; Dey et al., 1991; Lakhina et al., 2000; Mace et al., 1991; Schamel, 1986; Volosevich and Galperin, 1995, 2000a\link12; Yu and Shukla, 1983]. However, some problems related to these descriptions remain debatable and are to be further analyzed. Among them are the stability and lifetime of the quasi-stable nonlinear structures, the parameter ranges of the existence of solitary structures and/or nonlinear waves with arbitrary amplitudes in the multicomponent magnetospheric plasma, the conditions for existence and lifetime of asymmetric waveforms capable to take part in the auroral acceleration processes, etc. Such problems need to be solved in order to perform comparisons of the theory with experimental observations from satellites.

The approach we pursue in a series of papers on the subject [see Volosevich and Galperin, 1995, 2000a, 2000b, and references therein] is to develop an analytic theory for a fully nonlinear description of quasi-stationary solitary or periodic (knoidal) waveforms. The waveforms can be both symmetric and asymmetric in their potential, and the latter could take part in the auroral acceleration. The waveforms are usually the output result of experimental measurements from satellites and rockets with high timeresolution, so this approach is aimed to provide tools for comparisons with these experimental data.

Another, and related, aim of this approach is the delineation of the parameter ranges of existence of solitary structures or knoidal waves in various plasma populations characteristic for the auroral magnetosphere (when they have been excited by some unspecified process). It was shown numerically in our previous papers that the waveforms of the nonlinear structures and waves (scale, velocity, amplitude) depend critically on the particular parameters of the ambient charged particle populations (temperature, density, beam velocity, ion mass). Such multicomponent plasmas are typical for the magnetosphere and auroral ionosphere where the small-scale nonlinear structures were observed.

This study is based on the so-called quasi-potential analysis approach [Das et al., 1998] to study the formation of one-dimensional electrostatic structures with arbitrary amplitudes in the plasma that consists of several different populations of charged particles. It is devoted to the plasma conditions in the auroral magnetosphere when a hot electron beam from the plasma sheet (which produces stationary aurora below such as auroral stable arc or inverted-V) passes through hot electron background. Simultaneously, there is an upward moving colder ion beam which consists of accelerated ionospheric ions and/or folded ion conic formed in the auroral ionosphere below. Such a situation is typical at altitudes ~1000-5000 km above a stable discrete auroral form with an upward field-aligned current carried by the hot electron beam.

The solutions found for these conditions in the three-component plasma, as will be shown below, describe quasi-stationary solitary structures with the waveforms resembling those observed. It appears from this fully nonlinear theory that such structures can exist in a more extended range of plasma parameters than the range previously studied in the small-amplitude limit.

2. Theoretical Model

We consider here the waveforms and parameter space of quasi-stationary solutions for moving electrostatic structures in multicomponent Hall-MHD plasmas for the conditions of the Earth's auroral magnetosphere. This approach to study nonlinear small-scale plasma structures is being developed in a series of papers [see Berthomer et al., 1998; Das et al., 1998; Dey et al., 1991; Mace et al., 1991; Schamel, 1986; Volosevich and Galperin, 1995, 2000a\link12; Yu and Shukla, 1983, and references therein], and recently, it was extended to include multi-component plasma of several populations with different densities, velocities, temperatures, ion masses [Volosevich and Galperin, 2000b].

We suppose here collisionless, homogeneous, fluid plasma populations in the one-dimensional case which are distributed, or moving, along the homogeneous magnetic field (i.e. unmagnetized). The plasma consists of background hot electron component, a hot electron beam (downward moving), and an upward moving colder ion beam. It is described by the following system of fluid and Poisson equations [see Dey et al., 1991; Volosevich and Galperin, 2000b]:

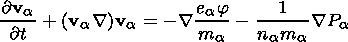(1)

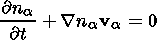(2)

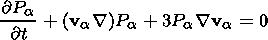(3)

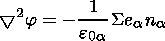(4)

Here m_a, e_a, T_a, and P_a= n_aT_a are the mass, charge, temperature, and pressure of the particle population of the sort a; j is the electrostatic potential corresponding to the electric field E=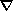 j. For the system (1)-(4) the magnetic field is along the z axis: B =B e_z, and for the one-dimensional model considered here the adiabatic law with g =3 is assumed. In the general case it is difficult to solve the system of equations (1)-(4) with the allowance for nonlinear effects. In the well-known solutions for the nonlinear nondispersive medium, when various physical quantities depend only on the variable S=(x-Vt)/l_D, the velocity V of the quasi-stationary wave is a constant, and the waveform does not change with time as in a linear medium. For such nonlinear quasi-stationary waves or solitary structures, the system of equations (1)-(4) is simplified. It can be reduced to a system of ordinary differential equations, in which the running coordinate S plays the role of the independent variable. This system determines the relation between the normalized electrostatic potential F and the density N_a of charged particles of type a [see Volosevich and Galperin, 2000a]

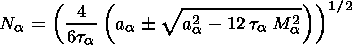(5)

where

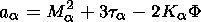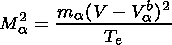V_a^b is the bulk velocity of a population (for a beam), N_a=n_a/n_0a, F =ej /T_e, t_a=T_a/T_e, M_a is similar to the Mach number, and for ions M_i²=(m_iV²)/(T_e). K=1 for ions, K=-1 for electrons, index zero is for non-disturbed values outside the structure.

The theoretical model considered here involves three sorts of charged particles: (1) background hot electrons distributed according to the Boltzmann law (with temperature T_e ), (2) hotter plasma sheet downward electron beam (temperature T_e^b=t_eT_e, velocity V_0e<0) (we assume t_e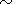 3 to simulate an auroral electron beam passing through a diffuse auroral background; these electrons are distributed according to equation (5) with relative beam density d, and the absolute values of V_0e^b,V_Te^b,V are of the same order of magnitude; M_e^h=({m_e[V-(-V_0e^b)]²}/T_e )^1/2, and (3) upward beam of colder ions (temperature T_i^e=t_i T_e, V_0i^b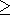 0 ); the ions are distributed according to the (5) too, where M_i=({m_i(V-V_0i^b)²}/T_e)^1/2 ( V_0i^b is the ion beam velocity (  V_0i^b 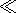V_0e^b ); V_0i^b is directed upward, as well as V ).

This scenario corresponds, for example, to the magnetospheric conditions above a stable auroral arc or inverted-V with an upward moving solitary structure.

Then the Poisson equation (4) may be finally transformed to

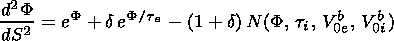(6)

where t_e is the temperature ratio of the beam to background electrons, d =n_0e^h/n_0e is the density ratio of beam electrons to background electrons.

3. Results of Numerical Solutions

The system of equations (1)-(3), (6) was solved numerically. The particularity of the electron beam distribution function according to equation (5) leads to the localized extremum of the classical potential V(F ), and this corresponds to the wave processes or soliton formation. Different types of the electrostatic structures and waveforms are found that are caused by the presence of the hot electron and ion beams.

Figure 1

One of these types is a solitary structure with positive potential which occurs for M_i²>3t_i in a wide range of relative electron beam density d and velocity V_oe . The amplitude of the structure depends on t_i, M_i and d . Cold ions are decisive for such structures. Figure 1a shows the amplitudes of the normalized potential | F | for solitons of positive polarity in respect to the electron beam relative density d and its velocity (given by the Mach number M_e),t_e=3. At M_e=3 the amplitude drops as the solutions found switch from one branch of equation (5) to another for the electron beam. The ion beam has Mach number M_i²>3t_i; t_i=0.1. Figure 1b shows the respective amplitudes of the normalized potential | F | in respect to the ion beam temperature t_i and M_e. Colder ion beams lead to higher positive potential amplitudes.

Figure 2

Another type of the electrostatic structures is a negatively charged solitary structure for M_e²>3t_e (assumed t_e=3 ). They need d >0.1 and also M_i²>3t_i, i.e., relatively dense electron beam and a fast/cold ion beam. The amplitudes of the normalized potential | F | for solitons of negative polarity in respect to the electron beam temperature t_e and its velocity (the Mach number M_e ) are shown in Figure 2 (the toned surface). 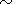For low t_e and high M_e the potential amplitude can exceed unity, while it drops to zero towards M_e 3 and t_e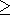 2.5.

The third type can be considered as a superposition of the two types described above. Depending on the initial value of j₀, it can be nearly soliton-like for low j₀, or a knoidal wave. In the latter case its frequency increases with the amplitude, and nonlinearity becomes more and more apparent (not shown).

An example of the parameters of a solitary structure is now described. It has the amplitude of the order of ej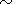 T_e in the background of electrons of the temperature T_e=3.9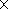 10⁶ K (i.e., T_e 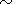0.3 keV), due to the downward auroral electron beam with the relative density d =0.5; V_0e^b=-2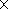 10⁴ km s ^-1; T_e^b=1.2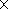 10⁷ K; M_e=1.5; and the ion beam with the upward velocity V_0i^b=25 km s ^-1; M_i=1.2. The structure has soliton-like waveform and moves upward with the velocity V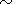 100 km s ^-1, in a qualitative accord with the results of the solitary structure measurements from the FAST satellite.

4. Discussion of Results

Auroral acceleration regions are characterized by energetic downward electron beam, hot electron background, the so-called diffuse auroral electrons and the charge neutralizing upward ion beam. Besides there are usually some minor populations: hot plasma sheet ions, electrons trapped between the magnetic mirror below and negative potential above, and secondary and scattered electrons of medium energy below the acceleration region, but these minor populations are neglected in the model described above. Such a three-component model is justified as it was shown recently that in the acceleration region above the arcs and inverted-V the thermal plasma from the ionosphere is indeed practically absent. However the role of the other types of the plasma populations remains to be investigated in the framework of this one, or in a more elaborated model using the approach described by Volosevich and Galperin [2000a, 2000b].

It is shown above that in such a three-component plasma model both positively and negatively charged electrostatic solitary structures as well as knoidal waves can be present, forming quasi-stationary moving structures. Negatively charged solitary structures move opposite to the electron beam direction, that is, upward, but with a relatively low velocity in the Earth's (or laboratory) frame. The positively charged structures move with the ion beam, that is, here also upward, with a velocity V comparable to the ion beam velocity V_0i^b. Qualitatively, both these properties of the solitary structures predominant motion are consistent with the measurements in the plasma flux tubes with an auroral electron beam.

The properties of the positively and negatively charged solitary structures are mainly determined, respectively, by the parameters of the ion and electron beams. Their amplitudes can reach quite significant values, up to tens of percent (or even more) of kT_e, the thermal energy of the background electrons. The amplitudes depend on other parameters such as d , M_e, t_i, as shown in Figures 1 and 2. At small amplitudes the waveforms tend to the classic solution form, while for large amplitudes and for knoidal waves they can differ significantly (not shown). The knoidal waves develop in these same solutions if the initial value j₀'(S=0) is increased. Then both the wave frequency and amplitude increase, and the waveforms are more and more nonlinear. The losses are inevitable in such cases but are neglected in this model.

The scenario of the waveform evolution could be as follows. In the hypothetical localized active plasma region with a strong turbulence and/or strong charge neutrality violation located below the satellite, the electric field varies strongly, and as a result, highly nonlinear knoidal waves are generated. These waves of high amplitude and sharp potential variations at the peaks in reality must have enhanced losses (though not described by the equations used above), so their amplitude, and also the frequency, must gradually decrease. The ultimate result is a quasi-stationary soliton-like waveform which can move a considerable distance from the source. Thus such structures, as was suggested in Volosevich and Galperin [2000a], occupy a much larger volume of space and hence are seen more often from a satellite passing through the plasma flux tubes of the acceleration region, while knoidal waves indicate a source nearby. This scenario qualitatively resembles the observations cited above of the solitary structures made above the stable auroral arcs and inverted-V. For more detailed comparisons the plasma parameters of all the plasma populations present must be known, and this seems to be realizable with the data gathered by recent satellite experiments.

5. Summary and Conclusions

The types of quasi-stationary fully nonlinear solutions and their parameter ranges are studied for the existence of one-dimensional electrostatic structures in a particular kind of magnetospheric plasma conditions resembling magnetospheric plasmas above an auroral arc or inverted-V. The self-consistent system of equations taking into account the electron temperature and pressure for the three-component plasma with electron and ion beams and a hot electron background is solved numerically. The results of the numerical solutions found arrive at the following conclusions:

• The nonlinear electrostatic structures with arbitrary amplitudes in these conditions can exist in a wide range of the plasma parameters. This range is more extended than the previously studied one in the small amplitude limit.
• The hot electron auroral beam accompanied by the counterstreaming colder ion beam in a hot electron background may be associated with the existence of solitary structures with large negative or positive amplitudes of the potential or by knoidal waves.
• The negatively charged solitary structures can exist only for the electron beam Mach numbers M_e²>3 T_i/T_e, while the positively charged ones can exist down to at least M_e=2.
• The calculated waveforms of the soliton-like electrostatic structures and knoidal waves modeled for the conditions resembling those in the auroral magnetosphere, agree qualitatively with the majority of the waveforms experimentally observed from the satellites S3 3, Viking, Freja, Interball 2, and FAST in these regions.

Acknowledgments

References

Berthomer, M., R. Pottelette, and M. Malingre, Solitary waves and weak double layers in a two-electron temperature auroral plasma, J. Geophys. Res., 103, 426, 1998.

Das, G. C., S. G. Tagare, and J. Jarma, Quasipotential analysis for ion-acoustic solitary waves and double layers in plasma, J. Planet. Space, 46, 417, 1998.

Dey, M., K. S. Goswami, and R. S. Bujarbarua, Theory of small-amplitude modified electron acoustic double layers and solitary waves in a multicomponent plasma, Physica B, 152, 385, 1991.

Ergun, R. E., et al., FAST satellite observations of electric field structures in the auroral zone. Geophys. Res. Lett., 25, 2025, 1998a.

Ergun, R. E., et al., FAST satellite observations of large-amplitude solitary structures, Geophys. Res. Lett., 25, 2041, 1998b.

Koskinen, H., and A. Malkki, Auroral weak double layers: A critical assessment, in Auroral Plasma Dynamics, Geophys. Monogr. Ser., vol. 80, edited by R. L. Lysak, p. 97, AGU, Washington, D.C., 1993.

Lakhina, G. S., B. T. Tsurutani, H. Kojima, and H. Matsumoto, "Broadband'' plasma waves in the boundary layers, J. Geophys. Res., 105, 27,791, 2000.

Mace, R. L., S. Babodal, R. Bharhram, and M. A. Hellberg, Arbitrary-amplitude electron-acoustic solitons in a two-component plasma, J. Plasma Phys., 45, 3, 323, 1991.

Schamel, H., Electron holes, ion holes, and double layers: Electrostatic phase space structures in theory and experiments, Phys. Rep., 140, 161, 1986.

Volosevich, A. V., and Yu. I. Galperin, Nonlinear quasi-stationary electrostatic structures in magnetospheric plasma, Cosmic Res., (Engl. Transl.), 33, 48, 1995.

Volosevich, A. V., and Yu. I. Galperin, Nonlinear electrostatic waves and localized moving structures in other plasmasphere and auroral magnetosphere, Cosmic Res. (Engl. Transl.), 38, 5, 514, 2000a.

Volosevich, A. V., and Yu. I. Galperin, Nonlinear electrostatic waves and structures in collisionless magnetospheric plasmas, Phys. Chem. Earth, 25 (1-2), 85, 2000b.

Yu, M. Y., and P. K. Shukla, Linear and nonlinear modified electron-acoustic waves, J. Plasma Phys., 29, 3, 409, 1983.