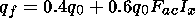International Journal of Geomagnetism and Aeronomy
Vol. 4, No. 1, April 2003
Model results for the midlatitude daytime
E region:
EUV ionization rate and a (NO
+ ) relationship
A. V. Mikhailov
Institute of Terrestrial Magnetism, Ionosphere
and Radio Wave Propagation,
Troitsk,
Russia
Contents
Abstract
The problem with low calculated
NmE for midlatitude
daytime
E layer is discussed using Millstone
Hill winter
Ne(h) observations compared
with model calculations. A proposal to obtain the
observed
NmE values due
to an
increase in the 50-100 Å
flux increase should be ruled out as this distorts
the proportion between UV and X-ray contributions to
the total photoionization rate of the
E region in
favor of X ray and leads to a contradiction in the
NmE observations during solar flares. The
Extreme Ultraviolet (EUV) model
by
Nusinov [1992]
provides a proper proportion
between UV and X-ray contributions while the
Extreme Ultraviolet Model for Aeronomic Calculations
(EUVAC) does not. A reduction of
a (NO
+ ),
by taking into account
Te >Tn in the
E region as it
follows from probe measurements, may be considered as
a plausible solution, although such probe
results are not confirmed by incoherent
scatter observations. The
E -layer ion composition with
[NO+] > [ O2+] corresponding to rocket observations
may be obtained in
model simulations by using an
appropriate [NO] height distribution.
1. Introduction
Midlatitude ionospheric
E layer
has been studied for many years, nevertheless there are still problems
with its description. While available empirical
NmE models like
International Reference Ionosphere
(IRI)
[Bilitza, 1990]
reproduce regular
NmE variations with
sufficient accuracy, a theoretical approach based on current EUV solar flux
models and commonly accepted dissociative recombination rate constants for
NO+ and O2+ ions usually
underestimates
NmE by 30-40%
[Buonsanto et al., 1995;
Titheridge, 1997].
Because of the square-law
loss process this 40%
deficit in
NmE implies a 100%
increase in the ionization rate at the
E -layer peak
(105-110 km).
Some approaches have been proposed to overcome this problem.
Ivanov-Kholodny and Nusinov [1979]
used low
a( NO+) value by
Mul and McGowan [1979]
along with strong seasonal
variations in
the [O2] scale height
in the 100-110 km
height range.
Antonova et al. [1996]
took into account
vibrationally excited NO+ and O2+ ions, and this allowed them to explain
NmE and
hmE seasonal
variations.
Titheridge [1996, 1997],
using a full allowance for secondary ionization with EUV radiations
down to 25 Å and a 33% additional
increase in the radiation with
l< 150 Å
in the
Extreme Ultraviolet Model for Aeronomic Calculations
(EUVAC)
[Richards et al., 1994],
could describe the observed
NmE values. Although there is large uncertainty
in EUV fluxes in this spectrum range, such
an increase of the EUV flux in the 50-150 Å
range seems
unjustified, as is shown below. The fluxes in this
spectrum range have already been tripled in the
EUVAC model
[Richards et al., 1994]
compared to
the reference spectrum F74113 measured on 23 April 1974
(F10.7=74), and this factor is kept in the model for
all levels of solar activity.
Calculated NO+/ O2+ ratio is another problem in the
E -region
theoretical modeling
[Buonsanto et al., 1995;
Titheridge, 1997].
Usually, the calculated NO+/ O2+ ratio is less, compared to rocket
observations in the
E region
[Danilov, 1994;
Danilov and Semenov, 1978;
Danilov and Smirnova, 1995, and references therein].
Buonsanto et al. [1995]
and
Titheridge [1997],
analyzing this problem,
suggested that our understanding of the NO+ chemistry may be incomplete.
The
aim of the paper is to compare
E -region
simulations with the Millstone Hill
Ne(h) observations
given by
Buonsanto et al. [1995]
and to draw a conclusion on EUV model fluxes and
a( NO+) dissociative
recombination rate
coefficient needed to obtain the observed
NmE for different levels of solar
activity. A possible way to obtain NO concentrations, providing the observed
NO+/O2+ ratio in model
International Reference Ionosphere
calculations, is proposed as well.
2. Ionospheric Model
Midlatitude regular ionospheric
E layer
is known to be controlled by photochemical processes.
A two-component model by
Nusinov
[Bruevich and Nusinov, 1984;
Nusinov, 1984, 1992]
with
further corrections by
Nusinov et al. [1999]
is used to calculate EUV fluxes in 48 wavelength intervals
with
8 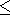 l
l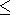 1050 Å.
The intensity of the EUV fluxes in this model depends on slowly varying
F bg emission at 10.7 cm wavelength and on radio emission
from active areas
on the Sun,
F10.7 [Nusinov, 1984].
The background
F bg emission varies from
F bg = 60-65 (in
10-22 W m-2 Hz-1 ) at solar
minimum to
F bg
1050 Å.
The intensity of the EUV fluxes in this model depends on slowly varying
F bg emission at 10.7 cm wavelength and on radio emission
from active areas
on the Sun,
F10.7 [Nusinov, 1984].
The background
F bg emission varies from
F bg = 60-65 (in
10-22 W m-2 Hz-1 ) at solar
minimum to
F bg 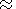 120 at solar maximum.
The X range ( l< 100 Å)
includes 13 wavelength bins.
Ionization by a strong Lyman-
a line ( l=1216 Å)
is taken into account according to the
Katjushina et al. [1991] model.
Although this emission gives only around 1%
of the total ionization rate at the
E -layer peak, it becomes important
at lower heights. For further discussion, Table 1 gives fluxes
according to the Nusinov and EUVAC models in the same wavelength
bins as used in the EUVAC
model. Solar minimum of 23 April 1974
( F10.7=74, F bg=67),
when the F74113 reference spectrum was
measured, and solar maximum conditions with
F10.7=200,
F bg=100 corresponding to the EUVAC model
for
P=200 are compared in Table 1.
Parameter
P = (FA10.7+F10.7)/2 is used as the proxy
in the EUVAC
model
[Richards et al., 1994],
FA10.7 being an 81-day average of the daily
F10.7 index.
120 at solar maximum.
The X range ( l< 100 Å)
includes 13 wavelength bins.
Ionization by a strong Lyman-
a line ( l=1216 Å)
is taken into account according to the
Katjushina et al. [1991] model.
Although this emission gives only around 1%
of the total ionization rate at the
E -layer peak, it becomes important
at lower heights. For further discussion, Table 1 gives fluxes
according to the Nusinov and EUVAC models in the same wavelength
bins as used in the EUVAC
model. Solar minimum of 23 April 1974
( F10.7=74, F bg=67),
when the F74113 reference spectrum was
measured, and solar maximum conditions with
F10.7=200,
F bg=100 corresponding to the EUVAC model
for
P=200 are compared in Table 1.
Parameter
P = (FA10.7+F10.7)/2 is used as the proxy
in the EUVAC
model
[Richards et al., 1994],
FA10.7 being an 81-day average of the daily
F10.7 index.
Our usual model calculations (a standard mode) are based on the
photoionization and photoabsorption
cross sections mostly from
Torr et al. [1979].
Photoionization cross section for O+(4S),
O+(2P), and
O+(2D) production were taken according to
Richards and Torr [1988],
with allowance for
the secondary ionization for
l< 250 Å
according to
Ivanov-Kholodny and Nikol'sky [1969].
Their
approach is based on the experimental fact that each
act of ionization by short-wave UV or X-ray
emission requires
e amount of energy.
This
e = 32 eV for the emission with
l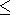 200 Å.
Then the
effective ionization cross section is defined as
200 Å.
Then the
effective ionization cross section is defined as
 | (1) |
where
E is the energy of the initial photon, and
siph is the photoionization
cross section, and
l is the wavelength in Å.
For the sake of
comparison, the same calculations were performed with the cross sections
given by
Fennely and Torr [1992],
taking into account secondary
ionization for
l< 400 Å,
as proposed by
Titheridge [1996].
The list of chemical reactions
used in the model is given in Table 2. Reaction rates were taken from
Buonsanto et al. [1992],
McEwan and Phillips [1975],
Oppenheimer et al. [1977],
Torr and Torr [1979], and
McFarland et al. [1973].
Neutral composition (O, O2, N2, N)
and temperature
Tn were used from the MSIS 86 thermospheric
model
[Hedin, 1987].
Nitric oxide, NO, is very important for
E -layer chemistry.
It was found by fitting
the calculated NO+/ Ne and
O2+/Ne ratios in the 100-120 km
height range to the ion composition model
by
Danilov and Smirnova [1995],
which is based on rocket measurements. An effective scale height of
the [NO] height distribution inferred at 115 km
was used to extrapolate the [NO] profile above 120 km.
The
Millstone Hill daytime observations for three winter -- days 5 February
1992,
10 November 1988, and 15 January 1985 -
as they are given in
Buonsanto et al. [1995],
were compared with our model
calculations. These days represent quiet time
E region
for solar minimum (15 January 1985,
FS=74.7 ),
middle (10 November 1988,
FS=175.3 ),
and high solar activity (5 February 1992,
FS=207 ) conditions,
FS being
a three-month average of
F10.7.
3. Calculations
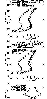
|
|
Figure 1
|
Three types of model calculations were performed for two sets (see above) of
photoionization and
photoabsorption cross sections: (i) with
standard EUV fluxes from Nusinov model and
Te=Tn in the
E region; (ii) with
fluxes
increased by four times
in the 50-100 Å
wavelength bin and
Te=Tn, and (iii) with
standard model fluxes, but
Te=2.5Tn in the
E -layer peak around 110 km. An increase of
Te over
Tn with
Te/Tn=3 - 5 is observed in the
probe measurements in the daytime
E region
[Duhau and Azpiazu, 1985].
As the dissociative recombination rate
coefficients for NO+ and O2+ ions depend on
Te , this
effect may be important. In accordance with
Duhau and Azpiazu [1985],
a gaussian-type dependence
was used to specify the
Te/Tn height distribution with
the peak at 110 km. Calculations and the
Millstone Hill observations are shown in Figure 1
for high solar activity (5 February 1992). The standard
calculations give
NmE by
lower
40%
than the observed one similar to FLIP (around a 50% deficiency)
and Millstone Hill photochemical model results
[Buonsanto et al., 1995].
The 50-100 Å flux increased
by a factor of 4 does provide the observed
NmE,
although
hmE is shifted to higher altitudes. Close
results, but with a more realistic
hmE,
may be obtained with the standard EUV model fluxes and
Te/Tn=2.5 at 110 km.
Calculations with cross sections by
Fennelly and Torr [1992]
and
Titheridge [1996]
(Figure 1,
middle
panel) give the results that
are very close to our standard model calculations
(Figure 1,
top), although our
approach of taking into account
the secondary ionization effects according to
Ivanov-Kholodny and Nikol'sky [1969]
is much simpler than the
Titheridge [1996]
approach. The 50-100 Å
flux increased by four times shifts
hmE to higher altitudes as in
Figure 1
(top), and the valley is not
developed in this case. Contrary, the
Ne(h) profile calculated with
Te/Tn=2.5 demonstrates a well
pronounced valley.

|
|
Figure 2
|

|
|
Figure 3
|
Relative ion composition
(the NO+/Ne and
O2+/Ne ratios) fitted to the
Danilov and Smirnova [1995]
model by varying [NO] are shown in Figure 1 (bottom).
It is interesting to note that [NO+ ] is higher than
[O
2+ ] above 105 km,
but the ratio is inverse at lower heights. This crossing point shifts to
lower heights
as the solar activity declines (see Figures 2 and 3).
The reason for such variations is out of the scope of this
paper, but the corresponding [NO] height profiles are discussed below.
Similar results are obtained for moderate solar activity
(Figure 2).
Although a factor of 4 for the 50-100 Å
flux provides the observed
Ne around 110 km, the
Ne(h) profile is uplifted as a whole and the valley
is
not well developed with the Fennelly, Torr, and Titheridge cross sections
(Figure 2,
middle panel).
Calculations with
Te/Tn=2.5 look more realistic
with both sets of cross sections (Figure 2, top and
middle boxes). The [NO+ ] ions dominate over [O2+ ] in the
100-120 km height range in agreement with
the Danilov and Smirnova model.
General conclusions concerning the results for solar minimum
(Figure 3)
are the same as above. The only
difference is that a factor of 4
for the 50-100 Å
flux is not sufficient to get the observed
Ne around 110 km,
while a factor of 2.5 for
Te/Tn
may be too high and should be decreased. Such a decrease of
Te/Tn ratio does take place at
low solar activity
[Duhau and Azpiazu, 1985].
It should be stressed that the
Danilov and Smirnova [1995]
model does not show any relative ion composition variations around 110 km
(cf. Figures 1,
2,
and 3,
bottom panels)
in the course of solar cycle (around 55% for NO+/Ne and 45% for
O2+/Ne). This implies corresponding
small [NO] variations with
solar activity in the
E -layer
maximum (see below).
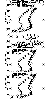
|
|
Figure 4
|
The other possibility for decreasing the NO+
ion recombination rate and solving the problem of low
calculated
NmE is to use the low dissociative recombination
rate coefficient
a( NO+)=2.3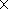 10-7 (300/Te)0.5 of
Mul and McGowan [1979].
Calculations with this rate coefficient provide
the observed
Ne around
110 km with
Te=1.5Tn and the standard model
of 50-100 Å
fluxes. The results are very close to those
obtained with
a( NO+)=4.5
10-7 (300/Te)0.5 of
Mul and McGowan [1979].
Calculations with this rate coefficient provide
the observed
Ne around
110 km with
Te=1.5Tn and the standard model
of 50-100 Å
fluxes. The results are very close to those
obtained with
a( NO+)=4.5  10-7 (300/Te)0.83,
Te/Tn=2.5 at 110 km. Both
curves are given for a
comparison in Figure 4
for three days considered. A well defined
hmE at 107-110 km
and a valley at 120-125 km
may be obtained in this case. The standard set of cross sections was used in
these calculations.
10-7 (300/Te)0.83,
Te/Tn=2.5 at 110 km. Both
curves are given for a
comparison in Figure 4
for three days considered. A well defined
hmE at 107-110 km
and a valley at 120-125 km
may be obtained in this case. The standard set of cross sections was used in
these calculations.
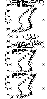
|
|
Figure 5
|
Each set of calculations was performed with [NO] fitted
to provide the
Danilov and Smirnova [1995]
model NO+/Ne and
O2+/Ne values in the 100-120 km
height range. Above 120 km [NO] was
extrapolated with an effective scale height found at 115 km.
The calculated [NO] distributions are given
in Figure 5
for three days in question. Only
calculations that provide
Ne at 110 km close to the
incoherent scatter (IS)
observations are shown in Figure 5.
The calculated [NO] height variation is seen to be a Chapman type
layer with a peak around 107 km and a scale height of
10  2 km.
A dependence of [NO]max on solar
activity is seen with [NO]max on 5 February 1992
being higher than on 15 January 1985.
2 km.
A dependence of [NO]max on solar
activity is seen with [NO]max on 5 February 1992
being higher than on 15 January 1985.
4. Discussion
There are two ways to overcome the problem with low calculated
NmE: either to increase the
photoionization rate in the
E -layer peak or to reduce the recombination rate of NO
+,
which is the major
ion in the
E region.
Let us consider the first possibility. For the classic daytime Chapman
E layer, the photoionization rate
in its peak may be written as
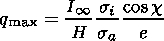 | (2) |
To increase
q max,
one may increase
I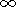 (the ionization flux) or
decrease
H (the scale height of the ionized
atmospheric neutral species). In their earlier
monograph
Ivanov-Kholodny and Nusinov [1979]
proposed considering strong seasonal variations
of molecular oxygen scale height in the
E region with
small winter H(O2 ) values.
Along with this they used low
a( NO+ ) by
Mul and McGowan [1979].
This
approach allowed them to explain many morphological features of the
E layer. Unfortunately low
winter H(O2 )
results in lower winter
hmE as
compared to the summer one. On one hand, this contradicts the
incoherent scatter observations made in Kharkov (49.43o N, 36.92oE)
and presented in the monograph by
Antonova et al. [1996],
where winter
hmE values are higher than summer ones. On the other
hand,
according to MSIS 86 thermospheric model
[Hedin, 1987],
the concentration of the major neutral (O2, N2,
O) species is higher in winter at the midlatitude
E region, and this should result in higher winter
hmE values.
(the ionization flux) or
decrease
H (the scale height of the ionized
atmospheric neutral species). In their earlier
monograph
Ivanov-Kholodny and Nusinov [1979]
proposed considering strong seasonal variations
of molecular oxygen scale height in the
E region with
small winter H(O2 ) values.
Along with this they used low
a( NO+ ) by
Mul and McGowan [1979].
This
approach allowed them to explain many morphological features of the
E layer. Unfortunately low
winter H(O2 )
results in lower winter
hmE as
compared to the summer one. On one hand, this contradicts the
incoherent scatter observations made in Kharkov (49.43o N, 36.92oE)
and presented in the monograph by
Antonova et al. [1996],
where winter
hmE values are higher than summer ones. On the other
hand,
according to MSIS 86 thermospheric model
[Hedin, 1987],
the concentration of the major neutral (O2, N2,
O) species is higher in winter at the midlatitude
E region, and this should result in higher winter
hmE values.
The other possibility is to increase
I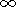 in (2). The ionization rate
should be doubled at the
E -layer peak
if the
Nusinov [1992]
EUV model is used (Figures 1, 2, and 3,
Te=Tn ).
This cannot be done for two UV lines
with
l=977 Å
(CIII) and 1026 Å (Lyman-
b ),
producing the main ionization in the
E region as the present
day accuracy of measurements in the UV range
of spectrum is high enough
[Woods et al., 1998].
On
the other hand there is large uncertainty with EUV fluxes for
l< 150 Å.
Initial fluxes have been tripled
for the
l = 50-150 Å
interval in the EUVAC model
[Richards et al., 1994],
but an additional increase up
to a factor of 4 is required to get
the experimental
NmE values
[Titheridge, 1997].
The same increase of the
fluxes with
l = 50-100 Å
by a factor of 4 is needed for the Nusinov model to obtain the observed
NmE (Figures 1, 2, and 3).
Such an increase of the soft X-ray
radiation changes (in favor of X rays) the proportion
between UV and X-ray contributions to the
E -layer
ionization rate. According to
Titheridge [1997],
about 66% of the
E -region ionization is produced by radiation with
l< 150 Å.
The X-ray contribution
will be even larger if one uses
the required factor of 4 for this wavelength interval in the EUVAC model.
In case of the Nusinov EUV model, such an increase by a factor of 4 would give a
55% X-ray
contribution to the
total ionization rate at 110 km.
It is possible to show that such an increase of the X ray contribution to
the
E -layer ionization rate leads to a contradiction with ionospheric
observations.
in (2). The ionization rate
should be doubled at the
E -layer peak
if the
Nusinov [1992]
EUV model is used (Figures 1, 2, and 3,
Te=Tn ).
This cannot be done for two UV lines
with
l=977 Å
(CIII) and 1026 Å (Lyman-
b ),
producing the main ionization in the
E region as the present
day accuracy of measurements in the UV range
of spectrum is high enough
[Woods et al., 1998].
On
the other hand there is large uncertainty with EUV fluxes for
l< 150 Å.
Initial fluxes have been tripled
for the
l = 50-150 Å
interval in the EUVAC model
[Richards et al., 1994],
but an additional increase up
to a factor of 4 is required to get
the experimental
NmE values
[Titheridge, 1997].
The same increase of the
fluxes with
l = 50-100 Å
by a factor of 4 is needed for the Nusinov model to obtain the observed
NmE (Figures 1, 2, and 3).
Such an increase of the soft X-ray
radiation changes (in favor of X rays) the proportion
between UV and X-ray contributions to the
E -layer
ionization rate. According to
Titheridge [1997],
about 66% of the
E -region ionization is produced by radiation with
l< 150 Å.
The X-ray contribution
will be even larger if one uses
the required factor of 4 for this wavelength interval in the EUVAC model.
In case of the Nusinov EUV model, such an increase by a factor of 4 would give a
55% X-ray
contribution to the
total ionization rate at 110 km.
It is possible to show that such an increase of the X ray contribution to
the
E -layer ionization rate leads to a contradiction with ionospheric
observations.
One of the ways to estimate the X-ray
contribution to the
E -layer total ionization rate is to analyze
NmE variations during solar flares
[Ivanov-Kholodny et al., 1976, 1977].
According to rocket and satellite observations, a strong
increase of the X-ray emission takes place in 1-8,
8-20, and 44-60-Å
spectrum intervals
during solar flares while only small changes of the UV radiation were
observed
[Chubb et al., 1957].
Therefore, we may suppose for our estimates that the UV ionization rate
does not change during solar flares. The
Ix flux in the 8-165 Å
spectrum range, which ionizes the
E region, is related to the 8-20 Å
flux as
Ix 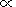 (I8-20)0.5
[Ivanov-Kholodny et al., 1976].
Regular
observations of X-ray
emission in the ionization chambers on board satellites are available and
published in Solar Geophysical Data. For strong flares analyzed by
Ivanov-Kholodny et al. [1977],
the
I8-20 emission measured on board the SOLRAD 9
and 10 satellites increased by five to 25 times. Therefore,
for our estimates we may take an average factor of 3.6
for the
Ix increase during the flare events
considered. Then the proposed increase by a factor of 4 of the X-ray
emission with a 55-66% (mean 60%) X-ray
contribution to the total
E -layer ionization rate results in
(I8-20)0.5
[Ivanov-Kholodny et al., 1976].
Regular
observations of X-ray
emission in the ionization chambers on board satellites are available and
published in Solar Geophysical Data. For strong flares analyzed by
Ivanov-Kholodny et al. [1977],
the
I8-20 emission measured on board the SOLRAD 9
and 10 satellites increased by five to 25 times. Therefore,
for our estimates we may take an average factor of 3.6
for the
Ix increase during the flare events
considered. Then the proposed increase by a factor of 4 of the X-ray
emission with a 55-66% (mean 60%) X-ray
contribution to the total
E -layer ionization rate results in
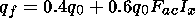 | (3) |
where
q0 and
qf are the total
E -layer
ionization rate for quiet and flare conditions, respectively, and
FacIx = 3.6 is an
average X-ray emission increase. Therefore, we get
qf = 2.56q0.
On the other hand, the observed
NmE variations for the flares considered
[Ivanov-Kholodny et al., 1977]
give, on the
average,
qf= (1.44- 1.60)q0 with a lower value
for winter and a larger
one for summer periods. This is much less than a factor of 2.56
obtained for the
fourfold
increase in X-ray emission required
to get the observed
NmE in model
calculations. Thus this proposal should
be ruled out. The observed
qf = (1.44 - 1.60)q0 implies only a
17-23% X-ray contribution to the total
E -region
ionization rate.
X-ray relative contribution
of 18%
was obtained by
Ivanov-Kholodny and Nusinov [1979]
for moderate solar activity. The EUV model by
Nusinov provides the required X-ray
relative contribution while the EUVAC model strongly
overestimates it (see Table 1 for the 50-100 Å
bin)
not to mention an additional increase of the flux in
this wavelength bin proposed by
Titheridge [1997].
Therefore, there is no way to solve the problem of
low calculated
NmE by a photoionization rate increase. It should
be mentioned that
according to recent soft
X-ray
measurements (20-100 Å) on board the
Student Nitric Oxide Explorer
(SNOE)
satellite
[Bailey et al., 1999],
the extrapolation of the measured irradiance to the solar minimum
gives much lower values
than the EUVAC predictions.
Let us consider the other possibility -- a decrease of
a( NO+). The
NmE observations can be well
reproduced in our calculations if
Te > Tn is accepted in the daytime
E region in agreement with the
probe measurements
[Duhau and Azpiazu, 1985].
A moderate
Te/Tn=2.5
ratio is required at the
E -layer
peak (around 110 km) with a conventional
a( NO+)=4.5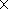 10-7 (300/Te)0.83 to
obtain the observed
NmE (Figures 1, 2, and 3). The required
Te/Tn ratio may be even 1.5 if
a small
a( NO+) = 2.3
10-7 (300/Te)0.83 to
obtain the observed
NmE (Figures 1, 2, and 3). The required
Te/Tn ratio may be even 1.5 if
a small
a( NO+) = 2.3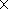 10-7 (300/Te)0.5 rate
coefficient given by
Mul and McGowan [1979]
is used (Figure 4).
Unlike
Duhau and Azpiazu [1985],
who
found strong dependence of
Te/Tn ratio on solar activity,
practically an unchanged
Te/Tn is required in
our calculations at all levels of solar activity. Physical mechanism of such
Te heating at middle latitudes is not
clear yet
[Duhau and Azpiazu, 1985].
It should be mentioned that no difference between
Te and
Ti (which coincides with
Tn in the midlatitude
E region)
is observed by the incoherent scatter method at
middle latitudes. Such
Te enhancement over
Ti due to the relative electron-ion drift takes place in
the auroral zone, according to the EISCAT observations
[Igarashi and Schlegel, 1987].
Nevertheless, a
possibility of
Te being higher
Tn seems very promising in solving the problem of low calculated
q/a eff for the daytime
E layer.
10-7 (300/Te)0.5 rate
coefficient given by
Mul and McGowan [1979]
is used (Figure 4).
Unlike
Duhau and Azpiazu [1985],
who
found strong dependence of
Te/Tn ratio on solar activity,
practically an unchanged
Te/Tn is required in
our calculations at all levels of solar activity. Physical mechanism of such
Te heating at middle latitudes is not
clear yet
[Duhau and Azpiazu, 1985].
It should be mentioned that no difference between
Te and
Ti (which coincides with
Tn in the midlatitude
E region)
is observed by the incoherent scatter method at
middle latitudes. Such
Te enhancement over
Ti due to the relative electron-ion drift takes place in
the auroral zone, according to the EISCAT observations
[Igarashi and Schlegel, 1987].
Nevertheless, a
possibility of
Te being higher
Tn seems very promising in solving the problem of low calculated
q/a eff for the daytime
E layer.
Our calculations (Figures 1, 2, and 3, top panels)
reproduce a reasonable depth of the
E-F1 valley. According to
the IRI 90 model
[Bilitza, 1990],
the valley depth ( N val/NmE ) is 10-12%
for the conditions in question.
The valley depth of 13-15%
is given by the empirical models
[Chasovitin et al., 1983;
Fatkullin et al., 1981].
Kharkov incoherent scatter observations
[Tkachev, 1981]
give the depth of the noon valley as
12-18%. The calculated
Ne(h) profiles (Figures 1, 2, and 3, top panels,
Te=2.5Tn ) have the valley
depth of 10-15%.
The profiles calculated with
FacX=4 for the 50-100 Å
wavelength interval show an undeveloped
valley. Normal valley with a depth of 10-13%
is provided by the Mul and McGowan [1979,
(Figure 4)]
calculations with
Te=1.5Tn,
FacX=1 , and
a( NO+).
Close results are obtained with the
Fennelly and Torr [1992]
and
Titheridge [1996]
cross sections (Figures 1, 2, and 3, middle panels).
Therefore, a proper EUV spectrum is
more important for development of a
normal valley than different sets of cross sections used in
calculations.
Problems with calculated NO+/ O2+ ratio
[Buonsanto et al., 1995;
Titheridge, 1997],
which contradicts
rocket measurements in the
E region,
mostly is related with a correct specification of the [NO]
distribution. In our approach we make a self-consistent
[NO] fitting to get NO+/Ne and
O2+/Ne ratios as
in the
Danilov and Smirnova [1995]
model, which is based on rocket observations. The calculated [NO]
profiles (Figure 5)
demonstrate small variations with solar activity, the [NO] peak density
at 107 km being
larger only by 40%
at high solar activity. This is much less than solar cycle variations
(4-5 times for
winter) used by
Titheridge [1997]
in his analysis. The other difference is in the NO peak density which
is
lower in his model
by 10-2.5 times
when we pass from low to high
solar activity. On the other hand, a
theoretical model by
Gerard et al. [1997]
gives the NO peak values, which are much closer to our
results. Close NO values were observed by SNOE satellite
at geomagnetic latitudes of Millstone Hill
for a quiet ( Ap=12 ) day following a period
of moderate disturbance with
Ap=28 [Solomon et al., 1999].
However, it should be stressed that
the obtained [NO] solar cycle variation is an estimate based on the
model
[Danilov and Smirnova, 1995]
ion composition, which demonstrates very small solar activity
variation in the
E region.
The effective scale height inferred at 115 km
from the calculated [NO] distribution is about 8-12 km,
depending on the calculation mode. This is close to
H( NO)=8- 9 km used by
Titheridge [1997, and
references therein],
but unlike his dependence on solar activity there is a tendency for
H( NO ) to be less
at solar maximum (Figure 5,
top and middle panels). Similar dependence of
H (NO) at 120 km on solar
activity may be found in
Gerard et al. [1997].
5. Conclusions
The main results of our analysis are the following:
1. The observed at Millstone Hill daytime
NmE may be reproduced in model calculations provided
that the
50-100 Å flux is increased by a
factor of 4 in the
Nusinov [1992]
EUV model. The same increase is required
in case of the EUVAC model as was proposed by
Titheridge [1997].
But such an increase distorts the
proportion between UV and X-ray
contributions in favor of X ray (around 60%) to the total
photoionization rate in the
E region.
This leads to a contradiction with
NmE observations during solar
flares. As was shown by
Ivanov-Kholodny and Nusinov [1979],
the X-ray contribution to the
E -layer
total ionization rate for quiet conditions is around 20%,
depending on solar activity; our analysis gives a
similar estimate. The EUV model by
Nusinov [1992]
provides this contribution while the EUVAC
model (where the 50-150 Å
flux was tripled) does not. Therefore, a proposal to obtain the observed
NmE values in model calculations
through an X-ray emission increase
should be ruled out.
2. The other way to obtain the observed
NmE is to reduce
a( NO+ ). One of the ways
to do this is to take
into account
Te >Tn in the
E region as it follows from the probe
measurements
[Duhau and Azpiazu, 1985].
A moderate
Te/Tn=2.5 ratio at the
E -layer peak (around 110 km)
along with a conventional
a( NO+) and the Nusinov EUV model
is required to get the observed daytime
NmE values at different
levels of solar activity.
The same results may be obtained with even lower
Te/Tn=1.5 ratio and
a( NO+ )
by
Mul and McGowan [1979].
Both calculations reproduce a reasonable depth of the
E-F1 valley with
N val/NmE = 10-15% close to the
empirical ionospheric models. But the reality of
Te > Tn in the
midlatitude daytime
E region
is questionable because the probe results are not confirmed by incoherent
scatter observations.
3. The
E -layer ion composition with [NO
+] > [ O2+ ] corresponding to
the rocket observations can be
reproduced in model calculations
using an appropriate [NO] height distribution. These [NO] profiles
may be obtained by fitting the calculated ion composition in the 100-120 km
height range to the model
based on rocket measurements.
The calculated [NO] is a Chapman type layer with a peak around
107 km and a scale height of 8-12 km
inferred at 115 km. The [NO] peak density varies with solar
activity being
larger
by 40%
at
F10.7=207 compared to solar minimum ( F10.7=75) conditions. The
obtained [NO] solar cycle variation should
be considered as an estimate based on model
[Danilov and Smirnova, 1995]
ion composition variations; the latter
show no solar activity variation at the
E -layer maximum around 110 km.
Acknowledgments
This work was in part
supported by the Russian Foundation for Basic Research under
Grant 98-05-64191.
References
Antonova, L. A., G. S. Ivanov-Kholodny, and V. E. Chertoprud,
Aeronomy of
E layer (in Russian),
Janus,
Moscow,
1996.
Bailey, S. M., T. N. Woods, C. A. Barth, and S. C. Solomon,
Measurements of the
solar soft X ray irradiance from the Student Nitric Oxide Explorer,
Geophys. Res. Lett., 26, 1255,
1999.
Bilitza, D., (ed.), International Reference Ionosphere IRI 90,
URSI-COSPAR, Rep. NSSDC/WDC A Rocket and Satellites,
Greenbelt, Maryland, 1990.
Bruevich, E. A., and A. A. Nusinov,
The spectrum of the short-wave radiation for
aeronomical calculations under various levels
of solar activity,
Geomagn. Aeron., 24 (in Russian),
581,
1984.
Buonsanto, M. J., S. C. Solomon, and W. K. Tobiska,
Comparison of measured and
modeled solar EUV flux and its effect on the
E-F1 region ionosphere,
J. Geophys. Res., 97, 10,513,
1992.
Buonsanto, M. J., P. G. Richards, W. K. Tobiska, S. C. Solomon,
Y.-K. Tung, and J. A. Fennelly,
Ionospheric electron densities calculated using different EUV
flux models and cross sections: Comparison with radar data,
J. Geophys. Res., 100, 14,569,
1995.
Chasovitin, Yu. K.,
V. B. Shushkova, E. N. Sykilinda, and
V. V. Maksimova, Empirical
model of the electron
concentration for low and middle latitudes at altitudes of 80-200 km,
Proc. Experim. Meteorol. Inst. (in Russian), 13 (102), 59,
1983.
Chubb, T. A., R. W. Kreplin, and H. Friedman, Rocket observation of X ray
emission in a solar flare,
J. Geophys. Res., 62, 89,
1957.
Danilov, A. D., Ion chemistry of the lower thermosphere,
J. Atmos. Terr. Phys., 56,
1213,
1994.
Danilov, A. D., and V. K. Semenov,
Relative ion composition model at midlatitudes,
J. Atmos. Terr. Phys., 40, 1093,
1978.
Danilov, A. D., and N. V. Smirnova, Improving the 75 to 300 km
ion composition model
of the IRI,
Adv. Space Res., 15 (2), 171,
1995.
Duhau, S., and C. M. Azpiazu, Empirical model of the
E region electron
temperature around noon and at low magnetic activity,
Planet. Space Sci., 33,
909,
1985.
Fatkullin, M. N., T. I. Zelenova, V. K. Kozlov, A. D. Legenjka,
and T. H. Soboleva,
Empirical Models of the Midlatitude Ionosphere,
256 pp.,
Nauka, Moscow,
1981.
Fennelly, J. A., and D. G. Torr,
Photoionization and photoabsorption cross sections
of O, N
2, O
2, and N for aeronomic calculations,
Atmos. Data Nucl. Data Tables, 51,
321,
1992.
Gerard, J.-C., D. V. Bisikalo, V. I. Shematovich, and J. W. Duff, An updated
model of the hot nitrogen atom kinetics and thermospheric nitric oxide,
J. Geophys. Res., 102, 285,
1997.
Hedin, A. E., MSIS 86 thermospheric model,
J. Geophys. Res., 92, 4649,
1987.
Igarashi, K., and K. Schlegel, Electron temperature enhancement in the polar
E region measured with EISCAT,
J. Atmos. Terr. Phys., 49, 273,
1987.
Ivanov-Kholodny, G. S., and G. M. Nikol'sky,
The Sun and the Ionosphere (in Russian),
217 pp.,
Nauka, Moscow,
1969.
Ivanov-Kholodny, G. S., and A. A. Nusinov, Formation and dynamics on the
daytime midlatitude ionospheric
E layer,
Proc. Inst. Appl. Geophys. (in Russian), 37, 1979.
Ivanov-Kholodny, G. S., L. N. Letshenko, and I. N. Odintzova, Relationship
between X ray and ultraviolet radiations of solar flares in the
ionization of the
ionosphere
E region,
Geomagn. Aeron. (in Russian), 16, 246,
1976.
Ivanov-Kholodny, G. S., L. N. Letshenko, A. A. Nusinov, and I. N. Odintzova,
Influence of seasonal variations of neutral atmosphere on ionization of the
ionospheric
E region,
Geomagn. Aeron. (in Russian), 17, 839,
1977.
Katjushina, V. V., M. V. Krasinets, A. A. Nusinov, Ch. A. Bart,
and
G. J. Rottman, A two-component model of the
Lya emission depending on solar
activity level,
Geomagn. Aeron. (in Russian), 31, 40,
1991.
McEwan, M. J., and L. F. Phillips,
Chemistry of the Atmosphere,
Edward Arnold,
London, 1975.
McFarland, M., D. L. Albritton, F. C. Fehsenfeld, E. E. Ferguson,
and A. L. Schmeltekopf,
Flow-drift technique for ion mobility and ion-molecular reaction rate
constant measurements,
II. Positive ion reactions of N+, O+, and N2+
with O2 and
O+ with N2 from thermal to 2 eV,
J. Chem. Phys., 59, 6620,
1973.
Mul, P. M., and J. W. McGowan, Temperature dependence of dissociative
recombination for atmospheric ions NO+, O2+
and N2+,
J. Phys., B12, 1591,
1979.
Nusinov, A. A., A dependence of intensity of EUV lines on solar activity level,
Geomagn. Aeron. (in Russian), 24, 529,
1984.
Nusinov, A. A., Models for prediction of EUV and X ray
solar radiation based on
10.7-cm radio emission,
Proc. Workshop on Solar Electromagnetic Radiation for Solar Cycle 22, Boulder,
Colo., July 1992, edited by
R. F. Donnely, NOAA ERL,
Boulder, Colo., USA, 354,
1992.
Nusinov, A. A., L. A. Antonova, and V. V. Katushina,
Solar fluxes in the 10- to 30-nm
range according to studies of the
E region
and the interlayer ionization valley,
Int. J. Geomagn. Aeron., 1, 153,
1999.
Oppenheimer, M., E. R. Constantinides,
K. Kirby-Docken,
G. A. Victor,
A. Dalgarno, and J. H. Hoffman, Ion photochemistry of the thermosphere
from
Atmosphere Explorer C measurements,
J. Geophys. Res., 82, 5485,
1977.
Richards, P. G., and D. G. Torr,
Ratios of photoelectron to EUV ionization rates
for aeronomic studies,
J. Geophys. Res., 93, 4060,
1988.
Richards, P. G., J. A. Fennelly, and D. G. Torr, EUVAC: A solar EUV flux
model
for aeronomic calculations,
J. Geophys. Res., 99, 8981,
1994.
Solomon, S. C., C. A. Barth, and S. M. Bailey,
Auroral production of nitric oxide
measured by the SNOE satellite,
Geophys. Res. Lett., 26, 1259,
1999.
Titheridge, J. E., Direct
allowance for effect of photoelectrons in ionospheric
modeling,
J. Geophys. Res., 101, 357,
1996.
Titheridge, J. E., Model results for the ionospheric
E region: Solar and seasonal
changes,
Ann. Geophys., 15, 63,
1997.
Tkachev, G. N., About the depth of the valley between layers
E and
F of the
ionosphere,
Geomagn. Aeron. (in Russian), 21, 939,
1981.
Torr, M. R., D. G. Torr, R. A. Ong, and H. E. Hinteregger,
Ionization frequencies
for major thermospheric constituents as a function of solar cycle 21,
Geophys. Res. Lett., 6, 771,
1979.
Woods, T. N., G. J. Rottman, S. M. Bailey, S. C. Solomon, and J. R. Worden,
Solar extreme ultraviolet irradiance measurements during solar cycle 22,
in Solar Electromagnetic Radiation Study for Solar Cycle 22, Kluwer I.R.
Academic
Publ., Dordrecht, 133,
1998.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on May 16, 2003.
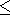 l
l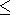 1050 Å.
The intensity of the EUV fluxes in this model depends on slowly varying
F bg emission at 10.7 cm wavelength and on radio emission
from active areas
on the Sun,
F10.7 [Nusinov, 1984].
The background
F bg emission varies from
F bg = 60-65 (in
10-22 W m-2 Hz-1 ) at solar
minimum to
F bg
1050 Å.
The intensity of the EUV fluxes in this model depends on slowly varying
F bg emission at 10.7 cm wavelength and on radio emission
from active areas
on the Sun,
F10.7 [Nusinov, 1984].
The background
F bg emission varies from
F bg = 60-65 (in
10-22 W m-2 Hz-1 ) at solar
minimum to
F bg 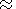 120 at solar maximum.
The X range ( l< 100 Å)
includes 13 wavelength bins.
Ionization by a strong Lyman-
a line ( l=1216 Å)
is taken into account according to the
Katjushina et al. [1991] model.
Although this emission gives only around 1%
of the total ionization rate at the
E -layer peak, it becomes important
at lower heights. For further discussion, Table 1 gives fluxes
according to the Nusinov and EUVAC models in the same wavelength
bins as used in the EUVAC
model. Solar minimum of 23 April 1974
( F10.7=74, F bg=67),
when the F74113 reference spectrum was
measured, and solar maximum conditions with
F10.7=200,
F bg=100 corresponding to the EUVAC model
for
P=200 are compared in Table 1.
Parameter
P = (FA10.7+F10.7)/2 is used as the proxy
in the EUVAC
model
[Richards et al., 1994],
FA10.7 being an 81-day average of the daily
F10.7 index.
120 at solar maximum.
The X range ( l< 100 Å)
includes 13 wavelength bins.
Ionization by a strong Lyman-
a line ( l=1216 Å)
is taken into account according to the
Katjushina et al. [1991] model.
Although this emission gives only around 1%
of the total ionization rate at the
E -layer peak, it becomes important
at lower heights. For further discussion, Table 1 gives fluxes
according to the Nusinov and EUVAC models in the same wavelength
bins as used in the EUVAC
model. Solar minimum of 23 April 1974
( F10.7=74, F bg=67),
when the F74113 reference spectrum was
measured, and solar maximum conditions with
F10.7=200,
F bg=100 corresponding to the EUVAC model
for
P=200 are compared in Table 1.
Parameter
P = (FA10.7+F10.7)/2 is used as the proxy
in the EUVAC
model
[Richards et al., 1994],
FA10.7 being an 81-day average of the daily
F10.7 index.

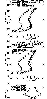


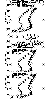
 10-7 (300/Te)0.5 of
Mul and McGowan [1979].
Calculations with this rate coefficient provide
the observed
Ne around
110 km with
Te=1.5Tn and the standard model
of 50-100 Å
fluxes. The results are very close to those
obtained with
a( NO+)=4.5
10-7 (300/Te)0.5 of
Mul and McGowan [1979].
Calculations with this rate coefficient provide
the observed
Ne around
110 km with
Te=1.5Tn and the standard model
of 50-100 Å
fluxes. The results are very close to those
obtained with
a( NO+)=4.5 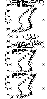
 2 km.
A dependence of [NO]max on solar
activity is seen with [NO]max on 5 February 1992
being higher than on 15 January 1985.
2 km.
A dependence of [NO]max on solar
activity is seen with [NO]max on 5 February 1992
being higher than on 15 January 1985.
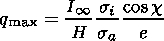
 (the ionization flux) or
decrease
H (the scale height of the ionized
atmospheric neutral species). In their earlier
monograph
Ivanov-Kholodny and Nusinov [
(the ionization flux) or
decrease
H (the scale height of the ionized
atmospheric neutral species). In their earlier
monograph
Ivanov-Kholodny and Nusinov [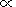 (I8-20)0.5
[Ivanov-Kholodny et al.,
(I8-20)0.5
[Ivanov-Kholodny et al.,