Generation of wave motions in the middle atmosphere induced by variations of the solar ultraviolet radiation flux (based on the UARS satellite data)

A. A. Krivolutsky, V. M. Kiryushov, and P. N. Vargin

Central Aerological Observatory, Dolgoprudny, Russia

Contents

Abstract

1. Introduction

It is widely known [Brasseur and Solomon, 1984; Khrgian, 1973] that the atmospheric ozone is the most sensible link in any analysis of the chemical, radiation, and dynamical processes in the middle atmosphere and also their interrelation. In particular, the solar ultraviolet radiation (UV) with the wavelength below 242 nm determines directly the photodissociation rate of molecular oxygen and so the ozone production rate. The UV radiation absorption in this atmospheric region leads to its heating which governs in its turn the temperature and dynamical regimes. Photochemical processes determine the ozone variations in the upper stratosphere and mesosphere due to the decrease of the ozone relaxation time with height. In the troposphere and lower stratosphere the contribution of dynamical processes to the ozone variability is determining. That is why the problem of separation of the part of the total ozone content variations which is caused by the solar UV radiation variations is rather complicate and had no unambiguous answer for a long time [Angell and Korshover, 1976]. At the same time the long-term ozone variations in the upper stratosphere in the solar activity cycle (10-12 years) are revealed fairly reliably based on satellite observation data [Chandra, 1994; Hood and McCormack, 1992; Hood et al., 1993]. The solar UV radiation variations contain not only the long-term variations (10-12 years) induced by the solar activity cycle but relatively shorter-term variations (about 27 days) related to the Sun's rotation around its axis [Chandra et al., 1995; Donelly, 1991]. These variations are due to the existence of so-called "active longitudes" (stable longitudinal intervals) on the Sun in which long-term activity centers are grouped [Vitinskiy, 1983]. The lifetime of such "active longitudes" may be comparable with the characteristic period of solar activity cycle, that is, considerably exceeds the lifetime of an individual activity center. Sometimes two "active longitudes" exist and that leads to a modulation of the observed solar radiation with a period of 13-14 days. In a general case when the angle difference between such longitudes is not equal to 180^o, one can say about other harmonic components of temporal variations of the solar radiation flux subjecting the initial series of observations to a spectral analysis.

The use of numerical models may provide a possibility, for example, to check the photochemical ozone production theory which must be fulfilled at heights of the upper stratosphere and mesosphere. During the recent decade the simultaneous satellite observations of the temperature, ozone content, and ultraviolet radiation made it possible really to start solving such problem. Brasseur [1993] and Brasseur et al. [1987] used one-dimensional and two-dimensional numerical photochemical models to study the ozone response to solar UV radiation variations, including those with the period of the Sun's proper rotation (about 27 days). The comparison of the real ozone and temperature variations in the upper stratosphere detected in the satellite (Nimbus 7) measurements with the photochemical calculation results revealed a discrepancy. For example, the temperature response with the 27-day period at these heights proved to be underestimated by a factor of two in the model simulations. Actually (under the data analysis) the effect magnitude is about 0.1 K per 1% variations of the UV radiation flux at a wavelength of 205 nm. Hood [1987] showed that the difference should be caused by the dynamical factors not taken into account in the one-dimensional model.

Krivolutsky [1989] used the tide theory to show that in the terrestrial atmosphere there exists a possibility of intensification of induced variations of such type if there exist large-scale longitudinal irregularities in the ozone distribution which modulate the atmospheric heating and determine the corresponding horizontal length of the excited wave. The analysis of the aerological data shows [Krivolutsky, 1989] that the revealed structure of the 27-day waves in the lower stratosphere is close to the corresponding structure of one of the proper modes (the Hough functions) and that does not contradict the idea of solar rhythm resonant intensification in the atmosphere. Krivolutsky and Kiryushov [1995] used a numerical two-dimensional model of planetary waves to study resonant properties of the terrestrial atmosphere when there is an internal source caused by irregularities of the heating due to the solar radiation temporal variations. A conventionalized structure of the excitation source was used. The calculations by Krivolutsky and Kiryushov [1995] revealed the middle atmosphere selective response to periodical impacts of this type, one of the peaks of the resonant curve corresponding to a period of 23-27-days (external impact).

This paper presents a development of the work by Krivolutsky and Kiryushov [1995]. The nonzonal structure of the ozone heating source is studied in more detail using the global satellite information on the ozone distribution and the data on the solar ultraviolet radiation flux.

2. Numerical Model

The planetary wave numerical model is based on the equation of potential vortex conservation. If a planetary wave propagates along a latitude circle, the longitude-temporal dependence of the wave parameters may be presented in the form

Here m is the zonal wave number, s is the oscillation frequency, the dashed values show the deviation from the zonal mean state, and the line means zonal averaging. For the wave amplitude which depends on latitude q and dimensionless height z = log(P₀/P), where P₀ is the pressure on the surface level, one can obtain the following equation [Shoeberl and Clark, 1980]:

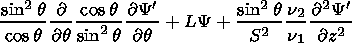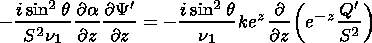(1)

where

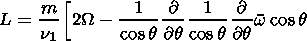is the potential vortex meridional gradient of the zonal mean flow;

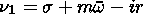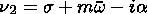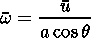a and W are the Earth's radius and angular rotation velocity, respectively; a is the Newton cooling coefficient; r is the Rayleigh's friction coefficient; u = u(q,z) is the zonal mean wind velocity;

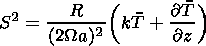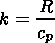S² is the static stability parameter; R is the gas constant; T is the global mean temperature; Q = J/c_p; and J is the nonadiabatic heating rate (degree per day). The wave amplitude Y is related to the geopotential disturbance amplitude F in the following way:

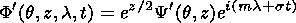Equation (1) is a second-order equation in partial derivatives of the elliptic type with complex coefficients. The equation was solved on the hemisphere with the help of the finite-residual approximation by the method proposed by Madala [1978]. The nonleakage condition (the velocity vertical component w = 0 ) was assumed at the upper and lower boundaries of the integration region. The wave amplitude was assumed to be equal to 0 (Y = 0) at the side boundaries (the equator and pole). The upper and lower boundaries of the integration region were posed at heights of 90 km and 12 km, respectively. The altitude and latitude steps were approximately 2.5 km and 1.8^o, respectively. The coefficients r and a parameterizing dissipative processes were chosen according to the recommendation by Garsia and Solomon [1983] but were slightly increased in the vicinity of the upper boundary, thus reducing (in the author opinion) the solution dependence on the upper boundary condition. The calculations were performed for various oscillation frequencies s and fixed spatial structure of the internal excitation source Q which had a real physics sense for the periods close to 27 and 14 days caused by the periodic heating of the middle atmosphere as the result of the ozone absorption of the variable solar ultraviolet radiation.

3. UV Radiation Variations

Twelve various instruments were installed on board the UARS (Upper Atmosphere Research Satellite) satellite launched by the National Aeronautics and Space Administration (NASA) on 12 September 1991 and aimed to study from the space the atmospheric state global variations. Six out of them provide a monitoring of the global distribution of minor gas constituents (including ozone) in the atmosphere, and two are aimed at a monitoring of its dynamical regime (the wind). Four additional instruments provide a permanent observations of solar corpuscular fluxes. Two of these instruments (SOLSTICE, Solar Stellar Irradiance Comparison Experiment, and SUSIM, Solar Ultraviolet Spectral Irradiance Monitor) measure the UV radiation flux in the following spectral ranges: 119-420 nm (SOLSTICE, spectral resolution is 0.1-0.3 nm) and 115-410 nm (SUSIM, spectral resolution is 0.15-5 nm). The measurements of the solar UV radiation by the SUSIM instrument are used in this paper to analyze temporal variations (the instrument characteristics and methodical details are given by Reiser et al. [1994]). The description of the UARS instrumentation is presented also on the UARS websites http://www-uars-science.html and http://daac.gsfc.nasa.gov/CAMPAIGN_DOCS/UARS_project.html.

Figure 1

Figure 2

Figure 3

Figure 4

Figure 5

Figure 6

Figures 1, 2, 3, and 4 show the solar UV radiation flux in various spectral ranges measured by the SUSIM instrument on board UARS in the first half of 1992. The temporal variations induced by the proper rotation of the Sun with the period of about a month (25-27 days) are distinctly seen in Figures 1-4. The amplitude of the corresponding peaks is several percent above the curve basis for all spectral ranges. It should be noted that we would obtain a twice lower value if these temporal series are subjected to a harmonic analysis. The results of the periodogram-analysis of the corresponding temporal series are shown in Figures 5 and 6 and make it possible to estimate characteristic periods of the harmonic components. In this case we are interested in the variation with the period of about 25 days, although one can discuss other harmonics, for example, the ones with the periods of approximately 13 and 35 days.

Figure 7

Thus the measurements of the solar UV radiation on board UARS during the first half of 1992 detected variations of the solar UV radiation level by several percent (Figure 7). We will use this estimate below determining the amplitude and structure of the forcing periodic source (with the period of 25 days) to calculate the middle atmosphere response in the numerical model.

4. Nonzonal Structure of the Ozone Field

To have the solution of the linear problem in the form of a running wave, the excitation source should be such a wave. The ozone heating function [Brasseur and Solomon, 1984; Khrgian, 1973] is the product of the solar ultraviolet radiation intensity outside the atmosphere and absorber (ozone) concentration. Thus the ozone heating function is a standing wave (the product of the temporal UV variations and longitudinal ozone variations) which may be formally presented as two waves running toward each other. However, the analysis of the proper curves of the Laplace tidal equation [Ivanovskiy and Krivolutsky, 1979] shows that the resonant conditions (close to the proper terrestrial atmosphere variations) may be fulfilled only for one of these waves and therefore under these conditions the standing wave would excite a running planetary wave in the atmosphere (in this case with the period close to 25 days and horizontal wavelength determined by the distance between the maxima of the ozone field irregularities.) In this case we are interested in quantitative evaluations of the Q' value (the excitation source) standing in the right-hand side of equation (1).

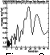
To study typical peculiarities and amplitudes of the nonzonal ozone distribution, at the first stage an analysis of the global satellite data on the total ozone content (TOC) measured by the TOMS instrument on board Nimbus 7 and Meteor satellites [McPeters and Beach, 1996] was carried out. The data are daily global fields of the total ozone content on the regular net with the latitudinal and longitudinal resolutions of 1^o and 1.25^o, respectively. The data are absent in the polar regions in winter period. Few gaps in the data available at lower latitudes were filled in with the help of a linear interpolation. Then the data were averaged over latitudinal (5^o) and longitudinal (20^o) intervals. The daily fields spatially averaged in this way were averaged for a month to filter out short-term variations of the total ozone content and to reveal quasi-stationary disturbances. The harmonic analysis of these monthly averaged data for each latitudinal zone allowed us to study the latitudinal structure of the TOC nonzonal deviations during 1979-1994.

Figure 8

Figure 9

Figure 10

Figure 11

Figure 12

Figures 8, 9, and 10 demonstrate as an example the latitudinal structure of the TOC nonzonal deviations in October of each year during 1979-1994 for the first three harmonics. One can see in the above figures that the first harmonic the maximum of which lies at 50^o-65^o S is clearly manifested in October, the effect amplitude reaching 100 DU in some years (including 1992). At the same time, the effect amplitude vary significantly in various years and contains a modulation with the period close to 2 years. However (as can be seen from Figure 11), during some periods (1981-1982 and 1990-1992) the temporal interval with increased amplitude lasts more than 1 year. For example, Figure 12 shows the amplitude evolution of the TOC first harmonic for the latitudinal belts 50.5^o-55.6^o N and 56.5^o-60.5^o S (in October) for 1988 when the effect amplitude exceeded 100 DU. One can see in Figure 12 that there exists a strong annual behavior of the stationary wave amplitude in ozone. In October the amplitudes of the TOC nonzonal component are lower in the Northern Hemisphere (in autumn) than in the Southern Hemisphere (in spring), however in spring in the Northern Hemisphere these amplitudes may also reach about 100 DU.

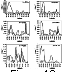
Thus during some years the ozone field which governs the heating and temperature in the stratosphere, has a strong longitudinal irregularity. It should be noted that only the data of satellite measurements made possible a correct study of the nonzonal ozone distribution structure since the ozone ground-based observation network provide no possibility to obtain the global picture because of the strong irregularity in the station disposition. First of all, it is true for the ozone fields and spatial peculiarities of its distribution in the southern hemisphere.

Figure 13

To estimate the corresponding nonzonal part of the heating, we used at first a regression restoration procedure of the vertical ozone distribution proposed by Bozhkov [1964]. The procedure makes it possible to obtain vertical ozone profiles up to a height of 45 km. The years with strongly pronounced nonzonality in the ozone distribution (1988, 1992, etc.) were chosen. From the vertical ozone distribution and model temperature distribution the global daily heating fields in the middle atmosphere were obtained with the help of the parameterization proposed by Strobel [1978] and in their own turn subjected to a harmonic analysis. Figure 13 shows the latitudinal behavior of the nonzonal harmonics of the ozone distribution for a height of 45 km for October 1988 (typical for the years with well pronounced nonzonality). Figure 13 shows that the magnitude of the first harmonics may reach 1 degree per day at upper stratosphere heights. This magnitude decreases at lower heights.

Thus the analysis performed of the solar UV radiation variations and global ozone distribution irregularities makes it possible to evaluate quantitatively the magnitude of the external periodic source. However, we should bear in mind that we consider the maximum magnitude of that source equal to a product of the maximum nonzonal heating rate (1^o per day) and relative UV radiation variations (of the order of 1%-2%). In the calculations, the maximum value (Q') of the periodic atmospheric heating was used and assumed to be 0.01^o per day.

5. Numerical Simulation Results

Figure 14

Figure 15

Figure 16

To estimate the middle atmosphere sensibility to slight periodic impact caused by solar UV radiation variations under nonzonal distribution of the absorber of this radiation (ozone), planetary wave equation (1) was used. The structure of the background zonal wind which enters the coefficients of equation (1) was taken using the parameterization proposed by Tung and Lindzen [1979] and approximately corresponded to winter conditions (Figure 14). The vertical-latitudinal structure of the source in the calculations had a conventionalized form (Figure 15) and corresponded to the results of the empirical data analysis shown in Figures 1-13. At the first stage, calculations were performed with invariable spatial structure of the periodical source shown in Figure 15 but for different periods. In spite of the fact that the source considered has probably a real physical sense only for typical solar periodicity (25-27 and 13-14 days), it is interesting to consider the atmospheric response for other periods since under such excitation the manifestation of proper atmospheric variations may be expected from the common ground. Figure 16 shows the resonant curve obtained in the calculations for a latitude of 46^o at a height of 51 km (the response structure almost does not depend on latitude but is visually manifested with an increase of the wave amplitude, that is, with an increase of the height above the surface level). Figure 16 demonstrates that the reliability of the oscillating loop determined by the model dissipative factors is not high. At the same time, the atmospheric response has selective character (in this case the resonant peaks correspond to periods of 10-13 and 25-35 days) and the response amplitude vary by several times depending on how close is the system to a resonance. It should be noted that equation (1) does not contain the temporal variable in explicit form therefore the calculations are of a climatological character.

Figure 17

Figure 18

Figure 17 shows a spatial structure of the running wave (the model simulation) with a period of 25 days (which corresponds to the observed UV radiation variations) and wave number m = 1 (corresponding to the analysis of the ozone data). Figure 17 shows that in this case the geopotential variation amplitude is approximately 20 gpm, the wave maximum being located slightly above the maximum of the excitation source (Figure 15). Above the maximum, the wave attenuates rapidly enough. That may be partly due to the viscosity increase in the vicinity of the upper boundary of the integration region. Figure 18 shows the corresponding spatial structure of the temperature disturbances induced by the wave. One should pay attention to the fact that there are two maxima in the temperature disturbance field caused by the initial hydrodynamical equations of the model (the temperature disturbance is proportional to a vertical derivative of the geopotential disturbances [Holton, 1975; Krivolutsky and Kiryushov, 1995].) According to the calculations, in this case the amplitude of the temperature variations in the maxima is approximately 0.4^o.

Figure 19

Figure 20

Figure 21

Figure 19 shows the structure of disturbances in the meridional wind field in the wave. The maximum velocity is about 0.5 m s^-1 and the spatial disturbance structure itself almost repeats the excitation source structure shown in Figure 15. Figures 20 and 21 show the spatial structures of the quadratic characteristics related to the wave generated.

6. Conclusions

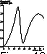
Thus the study carried out of the terrestrial atmosphere response to a periodic atmospheric heating with the period of the Sun's proper rotation (25-30 days) makes it possible to estimate possible efficiency of this mechanism. It is shown that the atmosphere has resonant frequencies in this range of the disturbance periods and thus the effect may be dynamically intensified by several times as compared with the purely zonal atmospheric heating. Such heating of the upper stratosphere should theoretically lead to the temperature variations with solar rotation period of ~0.1 K per each percent of the increase of the solar UV radiation at a wavelength of 205 nm [Brasseur et al., 1987]. The analysis of the temperature variations based on the measurements on board Nimbus 7 satellite [Hood, 1987] revealed the magnitude higher by a factor of 2. This discrepancy may be, as it has been already mentioned, related to possible dynamical effects. In this paper it is shown that, besides the possibility of a resonant intensification, the response depends significantly (linearly) also on the amplitude of the nonzonal part of the atmospheric heating. Under the UV variation magnitude of 1% chosen after the analysis of the magnitude of the temperature disturbance in the wave, is approximately 0.4 K.

References

Angell, J. K., and J. Korshover, Global ozone variations: An update into 1976, Mon. Weather Rev., 106, 63, 1976.

Bozhkov, R. D., Calculation of the vertical ozone distribution in the atmosphere based on its total content data, Meteorol. Gidrol. (in Russian), no. 1, 100, 1964.

Brasseur, G., The response of the middle atmosphere to long-term and short-term solar variability: A two-dimensional model, J. Geophys. Res., 98, 23,079, 1993.

Brasseur, G., and S. Solomon, Aeronomy of the Middle Atmosphere, 441 pp., D. Reidel, Hingham, Mass., 1984.

Brasseur, G., A. De Rudder, G. M. Keating, and M. C. Pitts, Response of the middle atmosphere to short-term solar ultraviolet variations, 2, Theory, J. Geophys. Res., 92, 903, 1987.

Chandra, S., The solar cycle variation of ozone in the stratosphere inferred from Nimbus 7 and NOAA 11 satellites, J. Geophys. Res., 99, 20,665, 1994.

Chandra, S., L. Lean, O. R. White, D. K. Prinz, G. J. Rottman, and G. E. Brueckner, SUSIM UV irradiance variability during the declining phase of solar 22, Geophys. Res. Lett., 22, 2481, 1995.

Donelly, R. F., Solar UV spectral irradiance variations, J. Geomagn. Geoelectr., 43, Suppl., Part 2, 835, 1991.

Garsia, R. R., and S. Solomon, A numerical model of the zonally averaged dynamical and chemical structure of the middle atmosphere, J. Geophys. Res., 78, 1379, 1983.

Holton, J. R., The Dynamic ogy of the Stratosphere and Mesosphere, . Monogr., vol. 37, Am.. Soc., Boston, Mass., 1975.

Hood, L. L., Solar ultraviolet radiation induced variations in the stratosphere and mesosphere, J. Geophys. Res., 92, 876, 1987.

Hood, L. L., and J. P. McCormack, Components of interannual ozone change based on Nimbus 7 TOMS data, Geophys. Res. Lett., 19, 2309, 1992.

Hood, L. L., J. Jirikowic, and J. P. McCormack, Quasi-decadal variability of the stratosphere: Influence of long-term solar ultraviolet variations, J. Atmos. Sci., 50, 3941, 1993.

Ivanovskiy, A. I., and A. A. Krivolutsky, On possibility of a resonant excitation of large-scale waves, Meteorol. Gidrol. (in Russian), 6, 97, 1979.

Khrgian, A. Kh., Physics of Atmospheric Ozone (in Russian), 291 pp., Gidrometeoizdat, Leningrad, 1973.

Krivolutsky, A. A., Atmospheric waves induced by solar rotation, Handb. MAP, 29, 86, 1989.

Krivolutsky, A. A., and B. M. Kiryushov, Contribution of nonzonal peculiarities of the ozone field in excitation of atmospheric resonant modes, Izv. Akad. Nauk Ross. Fiz. Atmos. Oceana (in Russian), 31 (1), 151, 1995.

Madala, R. V., An efficient direct solver for separable and non separable elliptic equations, Mon. Weather Rev., 106, 1735, 1978.

McPeters, R., and E. Beach (Eds.), TOMS Version 7, Data developed by the GSFC Ozone Processing Team, disk 1 of 2, June 1996.

Reiser, P., D. K. Prinz, J. Lumpe, and C. Wang, Post-launch characterization of stay light in the UARS/SUSIM, in Proceedings of the International Workshop on VUV and X ray Radiometry for Space-Based Instruments, pp. 47-50, Phys.-Tech. Bundesanstalt, Berlin, Germany, 1994.

Shoeberl, M. R., and J. H. Clark, Resonant planetary waves in a spherical atmosphere, J. Atmos. Sci., 37, 20, 1980.

Strobel, D. F., Parameterization of the atmospheric heating rates from 15 to 120 km due to O ₂ and O ₃ absorption of solar radiation, J. Geophys. Res., 83, 6225, 1978.

Tung, K. K., and R. S. Lindzen, A theory of stationary long waves, part II, Resonant Rossby waves in the presence of realistic vertical shears, Mon. Weather Rev., 107, 735, 1979.

Vitinskiy, Yu. I., Solar Activity (in Russian), 192 pp., Nauka, Moscow, 1983.