International Journal of Geomagnetism and Aeronomy
Vol. 3, No. 3, February 2003
Interplanetary conditions in association with prolonged
intervals of geomagnetic calm
G. K. Rangarajan and L. M. Barreto
Observatorio Nacional Säo
Cristovao, Rio de Janeiro, Brazil
Contents
Abstract
From the daily index
Ap of geomagnetic activity, sequences of
consecutive occurrence of
Ap  4 for 4 days and
Ap
4 for 4 days and
Ap  7 for
eight days are identified in the period 1963-1998. A superposed
epoch analysis is performed with the onset of these sequences as
key days and 8 different solar wind and IMF parameters and their variability
as inputs. A systematic pattern of change from days preceding the quiet
intervals to the days following is
clearly established. Solar wind velocity and its variability attain
the lowest values much later than the onset of the quiet sequence, and
the longer the interval, the later the minimum. IMF
B, on the other hand,
attains the lowest value at the onset of the quiet intervals, and continues
to remain low till the end of the sequence.
Thus a swing to low values of
B in association with small northward
Bz is an essential condition for onset of magnetically
calm intervals.
A possible threshold values with
V
7 for
eight days are identified in the period 1963-1998. A superposed
epoch analysis is performed with the onset of these sequences as
key days and 8 different solar wind and IMF parameters and their variability
as inputs. A systematic pattern of change from days preceding the quiet
intervals to the days following is
clearly established. Solar wind velocity and its variability attain
the lowest values much later than the onset of the quiet sequence, and
the longer the interval, the later the minimum. IMF
B, on the other hand,
attains the lowest value at the onset of the quiet intervals, and continues
to remain low till the end of the sequence.
Thus a swing to low values of
B in association with small northward
Bz is an essential condition for onset of magnetically
calm intervals.
A possible threshold values with
V  320 km s
-1,
B
320 km s
-1,
B  4 nT,
Bz > 0 (~0.8 nT),
lowest values of density preceding the onset of the quiet sequence and least
variability in all the parameters can be assigned during such prolonged
intervals of geomagnetic calm. In view of the smooth pattern of time
variation seen for
V and
B, an attempt is made to predict geomagnetic
quiet intervals from the solar wind parameters with moderate success.
4 nT,
Bz > 0 (~0.8 nT),
lowest values of density preceding the onset of the quiet sequence and least
variability in all the parameters can be assigned during such prolonged
intervals of geomagnetic calm. In view of the smooth pattern of time
variation seen for
V and
B, an attempt is made to predict geomagnetic
quiet intervals from the solar wind parameters with moderate success.
1. Introduction
The Earth's magnetosphere continues in a state of dynamic equilibrium
with the solar wind and the "frozen-in"
interplanetary magnetic field (IMF). The
interaction between solar wind and the magnetosphere
is a complex process which leads to several manifestations in the
geomagnetic field encompassing multiple time scales. From the
first in situ observations of solar wind and IMF parameters, it
was possible to establish their link with geomagnetic activity
[Snyder et al., 1963].
With the availability of additional
data from spacecraft observations, several parameters of
the solar wind and IMF were identified in controlling the
magnitude of geomagnetic activity in the auroral zone, in
the polar cap or at low latitudes and many statistically
significant relationships between the solar wind bulk speed ( V ),
the components of the IMF ( Bx,
By or
Bz in either GSE or GSM
coordinate systems), the variability in these parameters and
suitable combinations of the parameters.
[Baker, 1986;
Maezawa, 1978;
Svalgaard, 1977;
Sumaruk et al., 1990, etc.].
Feldstein [1992]
summarized the relative merits of 29 different models
of the equatorial ring current development and decay
and stressed that apart from the solar wind electric field,
as given by
V.
Bz, the velocity, also contributes independently
to the growth and decay of the ring current responsible for the DR field.
These investigations were possible mainly because of the painstaking
compilation of several spacecraft observations after suitable
normalization carried out by National Geophysical Data Center,
United States
[see, e.g., King, 1991]
and made available through World Data Center A.
The inverse process of identifying the IMF parameters from geomagnetic
activity has also been fairly successful. For example, diurnal variation
of the vertical component of
the magnetic field in the polar cap regions could be
used to indicate the polarity or the azimuthal component ( Bx or
By ) of
the IMF
[Mansurov, 1969;
Svalgaard, 1969],
Ap index could be used to
suggest the direction of
Bz [Mikerina and Ivanov, 1974]
or the polarity
of IMF
[Schreiber, 1978].
It is noteworthy that
while many studies involving
solar wind and geomagnetic activity have concentrated on the disturbed
state of the magnetosphere there have been relatively few studies which
examine, in depth, the interplanetary conditions preceding,
during and after intervals of geomagnetic quiescence. While it has
been well established that the magnitude and duration of the southward
component of IMF ( Bz < 0 ) is the primary agent for
enhanced magnetospheric and geomagnetic disturbances
[see, e.g., Chen et al. [1997,
and references therein], the
state of the magnetosphere during intervals when
Bz is
northward is not that well understood. In recent times,
emphasis has grown in identification and quantification
of the magnetosphere during intervals when IMF
Bz is
predominantly northward, as can be seen by the IAGA
symposium held in Canada in 1987 as also the IUGG
meeting in Birmingham, United Kingdom in July 1999. A special
issue of the Journal of Atmospheric and Terrestrial
Physics (Vol. 56 No. 2, 1994) was devoted to the geophysical
phenomena in the polar cap during northward interplanetary
magnetic field, wherein it has been emphasized that
"interaction
of Earth's
magnetosphere with the solar wind and northward IMF continues
to raise scientific interest and controversy."
According to
Burlaga and Ogilvie [1970],
"quiet"
solar wind is not a special well defined state of the solar wind
but rather an unusual and extreme condition. In one of the
earliest attempts to study the interplanetary parameters
during quiet solar wind conditions,
Neugebauer [1976]
identified 14 intervals when speed, proton density and
temperature variations were small over periods comparable
to the solar wind expansion time and found that the density
varies as inverse square of the velocity and that
the magnitude of
B is independent of
V and density. According to
Voight and Wolf [1988],
"it
is not a trivial problem to determine the physical properties of the
quiet magnetosphere. It would have
a net potential energy lower than the average. It
is an unresolved problem, however, to determine the lowest and highest
possible energy states for the magnetosphere compatible with the
thermodynamic condition of quasi-static convection."
Rich and Gussenhoven [1987]
suggest that a quiet state of the
ionosphere/magnetosphere system occurs when IMF
Bz is near zero or northward for an extended period and
when solar wind
velocity is low. The quiet conditions can be extremely long lasting
during solar minimum epochs and occur on the trailing edge of a
well defined stream.
Stern [1988],
however, sought the baseline
magnetosphere during the intervals when IMF was close to zero
since observations suggest that at such times the energy flow
into the magnetosphere and out of it is the smallest. Minimum
energy due to solar wind-magnetosphere coupling process linked with complete
dissipation of the earlier inputs were stipulated
as the likely conditions for the "ground state
magnetosphere"
by
Gussenhoven [1988].
She also specified that a set of four conditions,
listed below, are necessary to produce a magnetosphere
whose energy state is near minimal:
(1) Solar wind speed should be less than 400 km s
-1;
(2)
Bzm should be less than 2 nT
(where
Bzm stands
for N/S
component of the IMF
B in geocentric solar
magnetosphere coordinate (GSM) system;
(3) Magnitude of IMF
B should be less than 5 nT;
(4) All these conditions should last for at least 2 to 4 hours.
Gussenhoven [1988]
indicated that the baseline conditions tend to occur at
least 15 percent of the time. Later,
Kern and Gussenhoven [1990]
determined the conditions of
solar wind under the assumption
that baseline magnetosphere can be identified from prolonged periods
of low values of am index. Based on the analysis of 7 years of data
between 1978 and 1984, they modified the baseline conditions listed
above to
(1) solar wind speed should be less than 390 km s
-1,
(2) magnitude of IMF
B should be less than 6.5 nT,
(3) the angle 180-arctan
|By/Bz| should be less than
101o
when
Bz is negative or zero, and
(4) these conditions should last for at least 5 hours.
The analysis of
Kern and Gussenhoven [1990]
emphasized
in identifying quiet intervals from am index with
magnitude less than 4 nT preceded by exactly 6 hours
of am again less than 4 nT and confined their attention
to study the solar wind parameters one day on either
side of the set of key days.
In the present investigation, we identify prolonged
intervals of geomagnetic calm as a sequence of days
with
Ap  4 for at least 4 days and examine the
variability in 16 solar wind and IMF parameters over
four days on either side of the quiet intervals.
We also use a supplementary list of key days based
on the sequence of 8 consecutive days with daily
Ap
4 for at least 4 days and examine the
variability in 16 solar wind and IMF parameters over
four days on either side of the quiet intervals.
We also use a supplementary list of key days based
on the sequence of 8 consecutive days with daily
Ap  7 to see whether the marginal increase
in geomagnetic
activity modifies the basic features of
the solar wind parameters identified in the first
analysis. As the duration of geomagnetic calm
intervals defined here is much longer than that used by
Kern and Gussenhoven [1990]
and the parameter representing geomagnetic activity (daily
Ap index)
is different, we believe the results presented here will complement
excellently their earlier analysis and will give an estimate of the
conditions prevalent in the interplanetary medium preceding, during
and after an interval of prolonged geomagnetic calm.
7 to see whether the marginal increase
in geomagnetic
activity modifies the basic features of
the solar wind parameters identified in the first
analysis. As the duration of geomagnetic calm
intervals defined here is much longer than that used by
Kern and Gussenhoven [1990]
and the parameter representing geomagnetic activity (daily
Ap index)
is different, we believe the results presented here will complement
excellently their earlier analysis and will give an estimate of the
conditions prevalent in the interplanetary medium preceding, during
and after an interval of prolonged geomagnetic calm.
2. Data and Analysis

|
|
Figure 1a
|

|
|
Figure 1b
|

|
|
Figure 2
|
The criterion used for identification of prolonged intervals of
geomagnetic calm is the occurrence of daily values of
Ap  4 (equivalent
Kp = 10 )
for four consecutive days between 1963 and
July 1998, the period for which spacecraft observations of IMF
and solar wind are available from NGDC in the form of OMNI
tape and anonymous FTP. To supplement the results and for
examination of the state of the interplanetary medium during quiescent
intervals of longer duration, we also considered occurrence
of
Ap
4 (equivalent
Kp = 10 )
for four consecutive days between 1963 and
July 1998, the period for which spacecraft observations of IMF
and solar wind are available from NGDC in the form of OMNI
tape and anonymous FTP. To supplement the results and for
examination of the state of the interplanetary medium during quiescent
intervals of longer duration, we also considered occurrence
of
Ap  7 (equivalent
Kp
7 (equivalent
Kp  20 )
consecutively for 7 days. Our
choice of
Ap was motivated by the fact that the other two common
indices of geomagnetic activity,
AE and
Dst,
pertain to
rather specific regions whereas
Ap can be considered a planetary index.
In the years between 1963 and July 1998, there were 87 sequences with
Ap
20 )
consecutively for 7 days. Our
choice of
Ap was motivated by the fact that the other two common
indices of geomagnetic activity,
AE and
Dst,
pertain to
rather specific regions whereas
Ap can be considered a planetary index.
In the years between 1963 and July 1998, there were 87 sequences with
Ap  4 and 66 sequences with
Ap
4 and 66 sequences with
Ap  7, respectively. The daily averages
of corresponding solar wind and IMF parameters (16 in all -- IMF
B,
velocity
V, density
N,
Bx,
Bye,
Bym,
Bze,
Bzm,
and their variability (denoted by sig.
B, sig.
V, etc.)
were
extracted from the OMNI tape of NGDC, United States
(see King [1991] for details)
and were used as input in a superposed epoch analysis covering a period
four days prior to the onset of the sequence
of geomagnetic calm and four days after the
end of the sequence. The key day (0 day)
corresponds to the beginning of the sequence of quiet intervals.
Individual columns (12 in the case of
Ap
7, respectively. The daily averages
of corresponding solar wind and IMF parameters (16 in all -- IMF
B,
velocity
V, density
N,
Bx,
Bye,
Bym,
Bze,
Bzm,
and their variability (denoted by sig.
B, sig.
V, etc.)
were
extracted from the OMNI tape of NGDC, United States
(see King [1991] for details)
and were used as input in a superposed epoch analysis covering a period
four days prior to the onset of the sequence
of geomagnetic calm and four days after the
end of the sequence. The key day (0 day)
corresponds to the beginning of the sequence of quiet intervals.
Individual columns (12 in the case of
Ap  4 and 16 in the case
of
Ap
4 and 16 in the case
of
Ap  7 )
for which the data were available were then averaged
and the standard error of the mean computed. These are plotted
in the Figures 1a
and 1b.
In further discussions, the
intervals associated with
Ap
7 )
for which the data were available were then averaged
and the standard error of the mean computed. These are plotted
in the Figures 1a
and 1b.
In further discussions, the
intervals associated with
Ap  4 will be referred to as
"very
calm"
and that with
Ap
4 will be referred to as
"very
calm"
and that with
Ap  7 as "calm"
intervals.
Rangarajan and Iyemori [1997]
had identified several intervals of magnetospheric
quiet times between 1932 and 1997. Thirteen such intervals with
Kp
7 as "calm"
intervals.
Rangarajan and Iyemori [1997]
had identified several intervals of magnetospheric
quiet times between 1932 and 1997. Thirteen such intervals with
Kp  1+ for at least 32 consecutive 3-hour
intervals (four days) between 1963 and
1998 July were utilized as an independent
data set for checking the reality of the
results from the first two. The results
of this superposed epoch analysis, restricted to
only
V and
B (for brevity), are shown in Figure 2.
1+ for at least 32 consecutive 3-hour
intervals (four days) between 1963 and
1998 July were utilized as an independent
data set for checking the reality of the
results from the first two. The results
of this superposed epoch analysis, restricted to
only
V and
B (for brevity), are shown in Figure 2.
3. Results
Systematic change in almost all the 16 parameters,
beginning from four days prior to the onset of the key day and ending
four days after the termination of the sequence of calm intervals,
could be clearly noticed in both Figures 1a and 1b. The magnitudes
of the associated error bars (single standard error of the mean)
appears proportional to the mean value of the parameter, except
for
Bz and
By components. It should be pointed out that
the plots such as sig.
V, etc., denote the change in the average value
of the standard deviation of the corresponding parameter where the
standard deviation is derived from 24 hourly mean values of the day
and provided in the OMNI tape directly. This is
not to be confused with the error bars indicated.
Solar wind velocity changes from a value of above
400 km s
-1 prior to the commencement of the calm
period, to a minimum value of about 320 km s
-1 during the quiet times systematically and again
rises almost to the pre-calm level. The associated error
bars indicate that the event-to-event variation in the velocity
values was minimum during the period of magnetic calm on days
+2 and
+3 and this feature is mimicked in the sig.
V plot also.
Lowest value of velocity is attained on the last day of the
quiet sequence. This is again confirmed when we see the velocity
change across sequence of quiet days with
Ap  7 for 7 consecutive
days, when the minimum is seen only on day 7.
However, as would be anticipated, this minimum velocity is marginally
higher, around 350 km s
-1, confirming once again
the kind of empirical relationship established
between
Ap and
V by
Maer and Dessler [1964]
initially.
7 for 7 consecutive
days, when the minimum is seen only on day 7.
However, as would be anticipated, this minimum velocity is marginally
higher, around 350 km s
-1, confirming once again
the kind of empirical relationship established
between
Ap and
V by
Maer and Dessler [1964]
initially.
The density has a well defined maximum on the day
following the last day of the sequence (day 4 or 8)
but the pattern of change is smoother only when
"very calm"
intervals are considered. Pre-calm
epoch, particularly one or two days prior to the
commencement of the "very calm" sequence is also
marked by low density of comparable magnitude.
Persistent low density for 48 hours or so could
be suggestive of a precursor for prolonged quiet intervals.
When geomagnetic activity level is marginally
increased, as for the sequence with
Ap  7 (Figure 1b) the minimum on day 0 is quite well defined.
7 (Figure 1b) the minimum on day 0 is quite well defined.
The magnitude of IMF ( B ) has a low of nearly same
magnitude(~4 nT)
throughout the "very calm"
epoch and attains a stable post-quiet interval level
with nearly 50% increase. The variability in
B is also marked by a clear minimum at the commencement
of the quiet sequence.
When we consider the variations, across the key day,
of the components of IMF
B ( Bx and
By and
Bz in two
separate coordinate systems), we find that
(1) the choice of the coordinate system GSE or GSM
does not appear to be important in this analysis and
(2) the associated error bars are large and suggest
that not all the variations visible in the diagrams
may be statistically significant. However, the
following are worthy of note:
1. Magnitude of IMF
Bz during both the
"very calm"
and
"calm"
intervals is small ( < 1 nT)
but distinctly positive. This feature
may be considered another example favoring
the concept of the magnetosphere behaving as a half-wave rectifier
[Burton et al., 1975;
Crooker, 1980].
2. More than the magnitude, the variabilities
in all the parameters
Bx,
By, and
Bz (i.e., sig.
Bx, sig.
Bye/ sig.
Bym,
and
sig.
Bze/ sig.
Bzm )
show significant differences between pre/post passage
intervals compared to that during the quiescent part (0 to
+3 day in Figure 1a
and 0 to
+ 7 day in Figure 1b).
3. When the magnetic activity level is higher and the
duration
considered is longer, the variability in the components of IMF
exhibits a sharp minimum on day
+1 followed by a monotonic
increase in the quiet interval itself, a feature absent when
"very
calm"
intervals are considered (see Figure 1a).
4. Though the magnitude of
Bx for
"very calm"
intervals is not more than 1 nT,
a systematic chance from positive to
negative values from day 0 to day 7 could be seen,
suggestive of a change in the polarity of the IMF
near day
+2 or
+3. This feature, however, is not seen in
the other case, from day 0 to
+4.
Bx is practically close to zero, and a
swing from positive to negative values
of
Bx is confined to the post-quiet interval,
from day
+7 to
+10 only.
Figure 2 shows the change in the magnitude of IMF
and
B from 4 days prior to the onset of
"very
calm"
intervals up to four days
following the end of quietness,
based on another choice of days.
Thirteen key days utilized here correspond to the uninterrupted
sequence of at least 32 3-hour intervals with
Kp  1+.
These are not necessarily the same sequences used in the
earlier analysis with
Ap index and thus provide a check
on the reality of the variation in
V and
B, in association
with magnetospheric quiescence.
The patterns observed earlier are
reproduced quite faithfully with
the minimum in
V occurring on the
last day of the sequence with a
change in speed from about 450 km s-1
to around 300 km s-1 at the minimum. The change in
B appears more dramatic,
with a sharp fall from day
-3 to day
+1. However, if the associated
error is taken into consideration, the change is once again comparable
to that observed earlier.
The magnitudes of the error bars in Figure 2,
derived from a much smaller sample,
undergo significant change between
the days preceding the key days and
on day
+3 when the minimum velocity
is reached confirming the earlier
result that the variability in the solar wind velocity and magnitude of
IMF
B is very small indeed during
the intervals when geomagnetic
activity is close to its lowest level.
1+.
These are not necessarily the same sequences used in the
earlier analysis with
Ap index and thus provide a check
on the reality of the variation in
V and
B, in association
with magnetospheric quiescence.
The patterns observed earlier are
reproduced quite faithfully with
the minimum in
V occurring on the
last day of the sequence with a
change in speed from about 450 km s-1
to around 300 km s-1 at the minimum. The change in
B appears more dramatic,
with a sharp fall from day
-3 to day
+1. However, if the associated
error is taken into consideration, the change is once again comparable
to that observed earlier.
The magnitudes of the error bars in Figure 2,
derived from a much smaller sample,
undergo significant change between
the days preceding the key days and
on day
+3 when the minimum velocity
is reached confirming the earlier
result that the variability in the solar wind velocity and magnitude of
IMF
B is very small indeed during
the intervals when geomagnetic
activity is close to its lowest level.
As mentioned earlier, the standard error
associated with the mean tends to be very
small for
V and
B on the last day of the
sequence of "very calm" intervals. Even
for the other days preceding or following,
it is not widely variable. This suggests that
the average feature reported in Figure 1a for
B and
V is, perhaps, retained on most of the
87 days considered for analysis. One way of
verifying this would be the use of Principal Component Analysis
[Kendall, 1948].
Golovkov et al. [1978]
have clearly demonstrated how this method,
which they call the method of natural
orthogonal components (MNOC), help separate
a matrix of variables into distinct
components and show that if most of the rows
in the matrix have nearly the same pattern of
change across various columns, then the first
component will be the most dominant one and
a suitably calculated coefficient based on
the product of the row values and the
first eigenvector of the covariance matrix
of the given matrix helps in assessing
the contribution of the first component
to each of the rows in the matrix. To
ascertain that the reported average variation
in the two parameters
B and
V is indeed a
basic feature of the interaction between solar
wind and magnetosphere when
Bz is marginally
northward, we utilize the technique of MNOC.
We ensured that any missing values in the
matrices for
B and
V (consisting of 12 columns
and 59 or 43 rows for
B or
V )
were interpolated, and if the string of
missing values was long, then the row was left out of reckoning.

|
|
Figure 3
|
Figure 3 gives the first principal component (PC 1) in
V and
B between days
-4 and
+7. Almost the entire variance of the
system could be accounted for by this component alone
( > 90%) with very small contributions from second
and third components.
Also given in Figure 3 are the coefficients for each
row,
as a percentage. If it is 100%,
the variation in
V or
B around that key
day will be exactly the same as the first
principal component and percentage values greater or smaller than
this will correspondingly alter the magnitude of the PC 1.
This gives an idea of the stability or otherwise of the
average feature and the variability from one day to another.
We could immediately notice that the principal components show exactly the
same pattern of change of
V and
B as seen in Figure 1a.
In addition, it is
also seen that the variability of the coefficient is more pronounced for
V than for
B.
For many days, the coefficients of PC 1 for
B are close
to 100 with very few extreme
values.
V, on the other hand,
is marked by more variations.
This suggests that the change
in the magnitude of
B is much
better ordered with respect to
the sequence of "very calm"
intervals compared to the speed of the
solar wind. In a way, this is
also in conformity with the finding
of
Neugebauer [1976]
that the magnitude of
B does not depend on
V.
In view of the fact that the change in
V or
B in relation to
"very
calm"
intervals of geomagnetic activity
is quite smooth and significant,
it is tempting to see whether the
conditions in
V and
B preceding
the quiet period can be used as precursors of
quiet conditions. For this purpose, we impose the following two restrictions:
(1) The velocity for four consecutive days should be between greater than
400 km s
-1 and should decrease monotonically over next 3 days.
(2) The magnitude of IMF
B should be greater than 5 nT for at least 3
consecutive days and there should be a drop in magnitude more than
0.7 nT followed by nearly same values for next 3 days.

|
|
Figure 4
|
The mean values of
Ap for 4 consecutive days, beginning
a day after the commencement of decrease in
V and that
following the change in
B are shown in Figure 4. Ideally,
we should expect the original list of quiet sequence to
be reproduced but that does
not appear to be valid. However,
the predicted mean values of
Ap for sequence of four days, based
on change in velocity pattern, does
give a very good list of days with
mean value of about 5. There are, however, few exceptionally
high values. On the other hand, the approach to prediction
using
B leads to a list of days with average
Ap 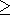 5 but no
widely departing values. Thus the combination of
B and
V satisfying the conditions imposed above may lead to prediction of geomagnetic
quiet intervals fairly reasonably, though the method fails to indicate days
with
Ap
5 but no
widely departing values. Thus the combination of
B and
V satisfying the conditions imposed above may lead to prediction of geomagnetic
quiet intervals fairly reasonably, though the method fails to indicate days
with
Ap  4.
4.
4. Discussion and Conclusions
Ap values
 7
(corresponding
Kp
7
(corresponding
Kp  20)
have been used to represent quiet conditions of
geomagnetic activity in several investigations.
Gussenhoven [1988]
identifies
Kp
20)
have been used to represent quiet conditions of
geomagnetic activity in several investigations.
Gussenhoven [1988]
identifies
Kp  1+ to correspond to quiet times.
In a study of the seasonal response of geomagnetic
activity to the polarity of IMF,
Bhargava and Rangarajan [1977]
found that days with
Ap=11-15 constitute the group which separates
the quiet and disturbed patterns in the seasonal variation and that
Ap
1+ to correspond to quiet times.
In a study of the seasonal response of geomagnetic
activity to the polarity of IMF,
Bhargava and Rangarajan [1977]
found that days with
Ap=11-15 constitute the group which separates
the quiet and disturbed patterns in the seasonal variation and that
Ap  10 can be considered representative
of a quiescent
magnetosphere. We can, therefore, be sure that the two
groups of prolonged intervals utilized in the present
analysis clearly represent two classes of quiet conditions
of the magnetosphere. Whether the
"very calm"
category of days with
Ap
10 can be considered representative
of a quiescent
magnetosphere. We can, therefore, be sure that the two
groups of prolonged intervals utilized in the present
analysis clearly represent two classes of quiet conditions
of the magnetosphere. Whether the
"very calm"
category of days with
Ap  4 represents
"baseline
magnetosphere"
is, however, not certain.
4 represents
"baseline
magnetosphere"
is, however, not certain.
If the undisturbed magnetosphere is defined with the condition that
the speed, proton temperature and density do not undergo large scale
variations in time compared to the solar wind expansion time
(~52 hours for
V  400 km s
-1 ), as suggested by
Neugebauer [1976],
then the corresponding parameters for the
quiet intervals seem to have very high and
variable values in contrast to the averages
derived here. For instance,
Neugebauer [1976]
gave a range of 15 to 67 cm-3
for
N, 348 to 606 km s-1 for
V,
and 4 to 7.7 nT for
B.
King [1986]
estimated the
typical magnitude of
B in quiet solar wind to be
about 5 nT, and
Burlaga and Ogilvie [1970]
suggested that
V should be
400 km s
-1 ), as suggested by
Neugebauer [1976],
then the corresponding parameters for the
quiet intervals seem to have very high and
variable values in contrast to the averages
derived here. For instance,
Neugebauer [1976]
gave a range of 15 to 67 cm-3
for
N, 348 to 606 km s-1 for
V,
and 4 to 7.7 nT for
B.
King [1986]
estimated the
typical magnitude of
B in quiet solar wind to be
about 5 nT, and
Burlaga and Ogilvie [1970]
suggested that
V should be
 250 km s
-1
during quiet intervals. In the distribution of solar wind velocity
in different bins over a solar cycle,
Gosling et al. [1976]
found that the speed
reached a value of
250 to 275 km s-1 only
on very few occasions, establishing at least a lower limit for
the speed from spacecraft observations. The present analysis suggests
IMF magnitude to be ~4 nT throughout the
"very calm"
intervals and in the initial parts of the
"calm"
intervals. The lowest value
of the speed is, on the average, about 325 km s-1 when
Ap is
250 km s
-1
during quiet intervals. In the distribution of solar wind velocity
in different bins over a solar cycle,
Gosling et al. [1976]
found that the speed
reached a value of
250 to 275 km s-1 only
on very few occasions, establishing at least a lower limit for
the speed from spacecraft observations. The present analysis suggests
IMF magnitude to be ~4 nT throughout the
"very calm"
intervals and in the initial parts of the
"calm"
intervals. The lowest value
of the speed is, on the average, about 325 km s-1 when
Ap is
 4 and marginally higher ~350 km s
-1 when
Ap is
4 and marginally higher ~350 km s
-1 when
Ap is
 7.
In both cases, the speed continues to decrease even in the
quiescent periods till the minimum value is reached on the last
day. The velocity change is somewhat similar to the time profile
of solar wind speed as a function of the passage of IMF sector
boundary past the Earth
[Wilcox and Ness, 1965]
where the
trailing part of the sector has low value and in the leading
part across the boundary a sharp increase in the solar wind speed.
Quiet intervals of geomagnetic activity also tend to follow
the trailing part of the IMF sector structure
[Gussenhoven, 1988].
The velocity threshold obtained here appears to be consistent with
the results of
Murayama et al. [1980],
who associated the lowest
level of geomagnetic activity in the auroral zone with
velocity
> 300 km s-1.
7.
In both cases, the speed continues to decrease even in the
quiescent periods till the minimum value is reached on the last
day. The velocity change is somewhat similar to the time profile
of solar wind speed as a function of the passage of IMF sector
boundary past the Earth
[Wilcox and Ness, 1965]
where the
trailing part of the sector has low value and in the leading
part across the boundary a sharp increase in the solar wind speed.
Quiet intervals of geomagnetic activity also tend to follow
the trailing part of the IMF sector structure
[Gussenhoven, 1988].
The velocity threshold obtained here appears to be consistent with
the results of
Murayama et al. [1980],
who associated the lowest
level of geomagnetic activity in the auroral zone with
velocity
> 300 km s-1.
According to
Yokoyama and Kamide [1997],
southward turning of IMF plays an important role in not only initiating
the main phase of a storm but also in determining the storm intensity.
It would, therefore, be natural to expect that
Bz to be zero or
positive when the geomagnetic activity is at its lowest. Also, we
are aware that the IMF is ordered in the GSE system but its
interaction with the magnetosphere is controlled in the GSM
coordinate system
[see, e.g.,
Russell and McPherron, 1973].
Figures 1a
and 1b
indicate that irrespective of the coordinate
system considered, the
Bz component of IMF, is small in magnitude
but distinctly positive during the "very calm" or
"calm" intervals
used in the analysis. This tends to confirm that
the magnetosphere does indeed behave like a half-wave
rectifier, as shown by
Murayama et al. [1980],
who
used the auroral electrojet index,
AL for their study.
In contrast to the approach to look for
the baseline magnetosphere when
Bz tends to be close
to zero when energy flow into and out of the magnetosphere
would be minimum
[Stern, 1988],
we find that during the
conditions of geomagnetic calm,
Bz is certainly positive
for the duration of the interval considered (4 or 8 days).
Rich and Gussenhoven [1997],
on the other hand, state that in
the quiet magnetosphere,
Bz can
be northward but the solar wind
velocity should be concurrently low. These two conditions are eminently
satisfied in the present analysis. We can, perhaps, make a distinction
between "baseline magnetosphere"
and "quiet magnetosphere"
and derive two separate thresholds of the IMF and solar wind.
The role of density in solar wind-magnetosphere interaction
is not clearly identified. In general, there is an inverse
relationship between the wind speed and proton density but
the two are not perfectly anti-correlated.
Rosenberg [1982]
suggested
that enhancement in density could be a precursor for geomagnetic storms
particularly in association with corotating interaction regions (CIRs).
Ivanov and Mikerina [1987]
found, in a case study, an unusual decrease in the density which was
associated with a very quiet interval. Superposed epoch
analysis of
proton density in the vicinity of
"very calm"
interval shows that the
density minimum does not coincide with either the velocity minimum or
B minimum (see Figure 1a)
but the change in density
within the interval itself is anti-correlated with
V.
A well-defined maximum in density on the termination
of the sequence of very quiet intervals is a noteworthy
feature, absent in
V. For the longer duration of calm
intervals, the time profile from 0 day to the end (day
+11 )
density and velocity are in phase opposition. Here again,
the maximum in density is obtained when the sequence of quiet
intervals is terminated (on day
+8 ). It appears that the change in
density from 2 days preceding the initiation of
"very calm"
intervals up to the end of the calm
intervals and for a few days later
is a very well-ordered structure, as
was seen for IMF
B and solar wind speed
and may be a precursory signal for a sequence of calm days.
In section 1,
we have shown
two sets of
conditions representing the baseline magnetosphere given by
Gussenhoven [1988]
and
Kern and Gussenhoven [1990].
According to these studies, The magnitude of IMF should be
< 5 nT and solar wind speed should be
< 390 km s-1 (lower of the two stipulations).
These are met adequately in the present work.
However, it should be borne in mind that even
when he took the periods when the three hourly
Ap was
0 for three consecutive intervals,
Sutcliffe [1998]
found that half the number of intervals could not clear
Gussenhoven's [1988]
criterion. Again, only half of the rejected part
could pass the criterion of
Kern and Gussenhoven [1990].
About 30% of the 24 intervals analyzed
by
Sutcliffe
did not satisfy one of the several conditions
imposed and in one case the velocity was more than
400 km s
-1.
This suggests that apart from the conditions
in the interplanetary medium corresponding to a quiescent
state, the magnetosphere also should attain a steady state
to be qualified as a
"baseline magnetosphere,"
whereas one can have a
"quiet magnetosphere"
under less stringent conditions of the magnitudes
of the solar wind and IMF parameters.
We can make some reasonable comparisons
of the time variations of the solar wind
and IMF parameters before and after quiet
intervals as identified by
Kern and Gussenhoven [1990]
and as given here in Figure 1a.
Let us recall that
Kern and Gussenhoven used
three hourly
Am index and confined their attention
to 24 hours preceding the calm period (which includes
6 hours with
Am  3 nT)
followed by 17 hours. In other
words, only the intervals covered by day
-1
and
+1 of the present analysis was included in
their results. Despite this difference, some
interesting common features are noticed. Their
velocity profile tends to be below the average
and decreases from before to after the quiet sequence and the
minimum is reached later than the start of the
epoch, as noticed in the present case also.
Density does not show any change preceding
the key hour and tends to rise in the post-quiet
interval, once again consistent with our picture
covering longer time span. Most interestingly, they find that IMF
B retains almost the same value for 24 hours preceding the key hour and
shows only a gradual rise in the 17 succeeding hours. This aspect
too is consistent with our results that
B remains at its low value
for the entire sequence of
"very calm"
days.
When the time variations in the components
of IMF are compared for these two choices
of significantly different key days, we notice
that the northward
Bz has a much larger mean
magnitude (1.8 nT) than what we obtain (~0.8 nT)
but in both cases, it is
always positive during the quiet intervals of geomagnetic activity.
Evidently, the longer duration for averaging tends to reduce the
magnitude of
Bz.
Kern and Gussenhoven show that neither
Bx nor
By has significant magnitude during the interval of time
under analysis and that
|Bx| >|By| during the quiet epoch
but before and after the quiet period,
|By| was more dominant.
On the contrary, we find that
Bx shows a clear change in
magnitude across the sequence of "very calm"
intervals. In the quiet
periods, however,
|Bx| is greater than
|By|,
as observed by them. The
associated error bars, however, make the significance of this results
doubtful. We concur with their inference that the significant parameters
for determining prolonged periods of magnetic quiet are IMF magnitude
and orientation and
V.
We have also examined, in addition, the time
variations in the variability of the components of IMF, solar wind
velocity and density and show that
"very calm"
intervals of geomagnetic activity
are marked by clear minimum in the variability also.
3 nT)
followed by 17 hours. In other
words, only the intervals covered by day
-1
and
+1 of the present analysis was included in
their results. Despite this difference, some
interesting common features are noticed. Their
velocity profile tends to be below the average
and decreases from before to after the quiet sequence and the
minimum is reached later than the start of the
epoch, as noticed in the present case also.
Density does not show any change preceding
the key hour and tends to rise in the post-quiet
interval, once again consistent with our picture
covering longer time span. Most interestingly, they find that IMF
B retains almost the same value for 24 hours preceding the key hour and
shows only a gradual rise in the 17 succeeding hours. This aspect
too is consistent with our results that
B remains at its low value
for the entire sequence of
"very calm"
days.
When the time variations in the components
of IMF are compared for these two choices
of significantly different key days, we notice
that the northward
Bz has a much larger mean
magnitude (1.8 nT) than what we obtain (~0.8 nT)
but in both cases, it is
always positive during the quiet intervals of geomagnetic activity.
Evidently, the longer duration for averaging tends to reduce the
magnitude of
Bz.
Kern and Gussenhoven show that neither
Bx nor
By has significant magnitude during the interval of time
under analysis and that
|Bx| >|By| during the quiet epoch
but before and after the quiet period,
|By| was more dominant.
On the contrary, we find that
Bx shows a clear change in
magnitude across the sequence of "very calm"
intervals. In the quiet
periods, however,
|Bx| is greater than
|By|,
as observed by them. The
associated error bars, however, make the significance of this results
doubtful. We concur with their inference that the significant parameters
for determining prolonged periods of magnetic quiet are IMF magnitude
and orientation and
V.
We have also examined, in addition, the time
variations in the variability of the components of IMF, solar wind
velocity and density and show that
"very calm"
intervals of geomagnetic activity
are marked by clear minimum in the variability also.
In conclusion, utilizing the daily
index
Ap of geomagnetic activity,
we identified two separate sequences
of prolonged geomagnetic quiet periods
and examined the time variations in 16
solar wind and IMF parameters in the vicinity of these sequences.
The results of superposed epoch analysis show that all the
parameters change in a very orderly fashion across the quiet intervals,
thereby enabling us to define the anticipated values of the parameters
that control the solar wind-magnetosphere interactions
during such quiet times. We associate a value of ~4 nT for
B,
~320 km s-1
for
V and a positive
Bz component
(with magnitude
< 1 nT). The density
remains significantly low from days
preceding the very quiet interval and attains a maximum on the
termination of the quiet sequence. It is, in general,
anti-correlated with the time variation in
V. The
variations in
B and
V are not very similar with
V reaching a minimum value much later in the sequence
of calm days, whereas
B reaches its minimum
in the initial part of the sequence and maintains
the low level right through the sequence.
The results of principal component analysis
suggest that the pattern of variation in
V and
B across the sequence of
"very calm"
intervals is largely preserved in
individual events also, as evidenced
by the most significant first component. The variability
in the magnitude from one key day to another is less pronounced with
regard to
B in comparison to
V.
The attempt to predict a sequence of
"very calm"
intervals using the average conditions of
V and
B preceding the period and the rate of change of these
two parameters in subsequent days yields fairly reasonable
success with better consistency when
V is utilized.
On the basis of the various definitions of baseline magnetosphere
discussed in the literature, we are led to conclude that
there may be perhaps two states one corresponding to the
lowest level of energy input from the solar wind to the
magnetosphere and the other corresponding to that
dictated by lowest levels of geomagnetic activity,
represented by a suitable index. The present results
complement nicely the earlier work of
Kern and Gussenhoven [1990]
and many features of the time variations within about
48 hours of a sequence of very calm intervals are shown
to be highlighted better when a much longer duration, in
terms of days, are considered.
Acknowledgments
The authors
are thankful to T. Iyemori, World Data Center for
Geomagnetism and Space Magnetism, Kyoto University, Japan, for providing
the daily mean values of the solar wind and IMF parameters for
1963-1993.
They are also thankful to the
World Data Center A for making
available the daily data on FTP
which was utilized to complete
the set. G.K.R. acknowledges
the offer of a fellowship by CNPq,
Brazil, to work as visiting professor at Observatorio
Nacional and thanks the Director,
Observatorio Nacional for facilities provided.
References
Baker, D. N.,
Statistical analyzes in the study of solar
wind-magnetosphere coupling
in Solar Wind Magnetosphere Coupling, edited by Y. Kamide
and J. A. Slavin,
p. 17,
Terra Sci., Tokyo,
1986.
Bhargava, B. N., and G. K. Rangarajan,
Sector polarity of IMF and annual variation
in occurrence of quiet and disturbed intervals,
J. Geomagn. Geoelectr., 29, 1, 1977.
Burlaga, L. F., and K. W. Ogilvie,
Heating of the solar wind,
Astrophys. J., 159, 659, 1970.
Burton, R. K., R. L. McPherron, and C. T. Russell,
The terrestrial magnetosphere: A half-wave rectifier,
Science, 189, 717, 1975.
Chen, J., P. J. Cargill, and P. J. Palmadesso,
Predicting solar wind structure and their
geoeffectiveness,
J. Geophys. Res., 102, 14,701, 1997.
Crooker, N. U., The half-wave
rectifier response of the magnetosphere
and antiparallel merging,
J. Geophys. Res., 85, 575, 1980.
Feldstein, Y. I., Modelling the magnetic field
of magnetospheric ring current as a function
of interplanetary medium parameters,
Space Sci. Rev., 59, 83, 1992.
Golovkov, V. P., N. E. Papitashvili, Y. S. Tyupkin, and
Y. P. Kharin, Separation of geomagnetic
field variations into quiet and disturbed
components by the method of natural orthogonal
components,
Geomagn. Aeron. (in Russian), 18, 342, 1978.
Gosling, J. T., A. R. Asbridge, and W. C. Feldman,
Solar wind speed variations: 1962-1974,
J. Geophys. Res., 81, 5061, 1976.
Gussenhoven, M. S., Low altitude convection,
precipitation and current patterns in the baseline
magnetosphere,
Rev. Geophys., 26, 792, 1988.
Ivanov, K. G., and N. V. Mikerina,
An unusually sharp decrease in the
density of the interplanetary plasma
near the Earth and a magnetically quiet day,
Geomagn. Aeron., 27, 6, 1987.
Kendall, M. G.,
The Advanced Theory of Statistics,
vol. II, Charles Griffin, London, 1948.
Kern, K. J., and M. S. Gussenhoven,
Solar wind conditions for a quiet
magnetosphere,
J. Geophys. Res., 95, 20,867, 1990.
King, J. H., Solar wind parameters
and magnetosphere coupling studies
in
Solar Wind Magnetosphere Coupling, edited by Y. Kamide and J. A. Slavin,
p. 163,
Terra Sci., Tokyo,
1986.
King, J. H., Long term solar wind variations
and associated data sources,
J. Geomag. Geoelectr., 43 (suppl.), 865, 1991.
Maer, K., and A. J. Dessler,
Comment on the paper by Conway W. Snyder et al.,
J. Geophys. Res., 69, 2846, 1964.
Maezawa, K., Dependence of
geomagnetic activity on solar
wind parameters: A statistical
approach,
Sol. Terr. Environ. Res. Jpn., 2, 103, 1978.
Mansurov, S. M., New evidence of a
relationship between magnetic fields
in space and on Earth,
Geomagn. Aeron. (in Russian), 9, 622, 1969.
Mikerina, N. U., and K. G. Ivanov,
Possibility of identifying the normal
interplanetary magnetic field component
from the planetary
Kp index,
Geomagn. Aeron. (in Russian), 14, 123, 1974.
Murayama, T., H. Nakai, and K. Hakamada,
Empirical formula to relate the auroral
electrojet intensity with interplanetary parameters,
Planet. Space Sci., 28, 803, 1980.
Neugebauer, M., The quiet solar wind,
J. Geophys. Res., 81, 4664, 1976.
Rangarajan, G. K., and T. Iyemori,
Time variations of geomagnetic activity indices
Kp and
Ap: An update,
Ann. Geophys., 15, 1271, 1997.
Rich, F. J., and M. S. Gussenhoven,
Absence of region 1/region 2
field aligned currents during prolonged quiet times,
Geophys. Res. Lett., 14, 689, 1987.
Rosenberg, R. L., A practical method of
predicting geomagnetic storms by using
precursory enhancement of solar wind density,
J. Geophys. Res., 87, 2563, 1982.
Russell, C. T., and R. L. McPherron,
Semi-annual variation in geomagnetic activity,
J. Geophys. Res., 78, 92, 1973.
Schreiber, H., On the possibility of
inferring the interplanetary sector
structure from daily variations of
geomagnetic ap indices,
Planet. Space Sci., 26, 767, 1978.
Snyder, C.W., M. Neugebaur, and U. R. Rao,
The solar wind velocity and its correlation
with cosmic ray variation and with solar and
geomagnetic activity,
J. Geophys. Res., 68, 6361, 1963.
Stern, D. P., Physics of the quiet magnetosphere,
Rev. Geophys., 26, 781, 1988.
Sumaruk, R. V., Ya. I. Feldshteyn, and B. A. Belov,
Intensity of auroral electrojets and ring current
as a function of the geoeffective parameters of the
interplanetary medium,
Geomagn. Aeron. (in Russian), 30, 164, 1990.
Sutcliffe, P. R., Observations of Pi2
pulsations in a near ground state magnetosphere,
Geophys. Res. Lett., 25, 4067, 1998.
Svalgaard, L., Sector structure
of the interplanetary magnetic
field and daily variation of the
geomagnetic field at high latitudes,
Pap. 6, Dan. Met. Inst. Geophys.,
Copenhagen, Denmark, 1969.
Svalgaard, L., Geomagnetic activity:
Dependence on solar wind parameters,
in
Coronal Holes and High Speed Solar Wind Streams,
edited by J. B. Zirker, p. 371,
Colo. Assoc. Univ. Press, Boulder, 1977.
Voight, G. H., and R. A. Wolf,
Quasi-static magnetospheric MHD processes and the "ground state"
of the magnetosphere,
Rev. Geophys., 26, 823, 1988.
Wilcox, J. M., and N. F. Ness,
Quasi-stationary corotating
structure in the interplanetary medium,
J. Geophys. Res., 70, 5793, 1965.
Yokoyama, N., and Y. Kamide,
Statistical nature of geomagnetic storms,
J. Geophys. Res., 102, 14,215, 1997.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on February 17, 2003.
 4 for at least 4 days and examine the
variability in 16 solar wind and IMF parameters over
four days on either side of the quiet intervals.
We also use a supplementary list of key days based
on the sequence of 8 consecutive days with daily
Ap
4 for at least 4 days and examine the
variability in 16 solar wind and IMF parameters over
four days on either side of the quiet intervals.
We also use a supplementary list of key days based
on the sequence of 8 consecutive days with daily
Ap  7 to see whether the marginal increase
in geomagnetic
activity modifies the basic features of
the solar wind parameters identified in the first
analysis. As the duration of geomagnetic calm
intervals defined here is much longer than that used by
Kern and Gussenhoven [1990]
and the parameter representing geomagnetic activity (daily
Ap index)
is different, we believe the results presented here will complement
excellently their earlier analysis and will give an estimate of the
conditions prevalent in the interplanetary medium preceding, during
and after an interval of prolonged geomagnetic calm.
7 to see whether the marginal increase
in geomagnetic
activity modifies the basic features of
the solar wind parameters identified in the first
analysis. As the duration of geomagnetic calm
intervals defined here is much longer than that used by
Kern and Gussenhoven [1990]
and the parameter representing geomagnetic activity (daily
Ap index)
is different, we believe the results presented here will complement
excellently their earlier analysis and will give an estimate of the
conditions prevalent in the interplanetary medium preceding, during
and after an interval of prolonged geomagnetic calm.
 320 km s
-1,
B
320 km s
-1,
B 




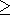 5 but no
widely departing values. Thus the combination of
B and
V satisfying the conditions imposed above may lead to prediction of geomagnetic
quiet intervals fairly reasonably, though the method fails to indicate days
with
Ap
5 but no
widely departing values. Thus the combination of
B and
V satisfying the conditions imposed above may lead to prediction of geomagnetic
quiet intervals fairly reasonably, though the method fails to indicate days
with
Ap