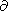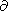Energy and momentum balance in the process of time-dependent magnetic Petschek-type reconnection

N. N. Volkonskaya, T. N. Volkonskaya, and V. S. Semenov

Institute of Physics, St. Petersburg University, St. Petersburg, Russia

Helfried K. Biernat

Space Research Institute, Austrian Academy of Sciences, Graz, Austria

Contents

Abstract

1. Introduction

Many processes observed inside the magnetosphere of Earth and other planets, and on Sun and other stars are associated with conversion of magnetic energy. There are many experimental results, which demonstrate that the processes of conversion of magnetic energy to kinetic and internal energy of the plasma occur in various situation [Coroniti, 1985; Hones, 1984]. For example, these phenomena take place during magnetosphere substorms in the magnetotail, at the magnetopause near the solar point (for a south direction of the IMF) and in the cusp region (for a north direction of the IMF), during solar flares and flares of some types of stars. It means that we deal with a fundamental physical process in the plasma. At present, there are several theories which describe the conversion of magnetic energy to kinetic energy of plasma. Most famous models are the pure resistive magnetic field Sweet-Parker dissipation [Parker, 1963; Sweet, 1958] tearing mode instability [Furth et al., 1963; Ottaviani and Porcell, 1995] and Petschek [1964] reconnection.

The model of reconnection suggested by Petschek [1964] explains the fast energy release in solar flares. Magnetic field dissipation needs only be present within a small region known as the diffusion region, and the energy conversion occurs primarily across nonlinear waves, or shocks in a highly conducting plasma.

Most of the used analytical models describe the steady-state regime of reconnection [Priest, 1985], but in nature we usually deal with explosive-like phenomena, where 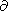/ t 0. So, for a clear understanding of the physics of the process, in particular from the energetic point of view, it is more accurate to use a time-varying rate.

Therefore Petschek's idea has been elaborated by Semenov et al. [1985], Biernat et al. [1987], and Heyn and Semenov [1996] for time-dependent conditions. There are a number of aspects of time-dependent reconnection which have no analogous behavior to the steady-state case [Biernat, 1993; Semenov et al., 1992]. The consideration of a time-varying reconnection rate makes possible the detailed analysis of the process of energy conversion and the change of momentum and energy of the plasma during the pulse of reconnection.

Figure 1

First, we consider a simple theoretical system consisting of a current sheet separating two uniform and identical plasmas with antiparallel magnetic fields (Figure 1). Anomalous resistivity is supposed to be formed in a small region, which is traditionally called diffusion region. As a result, a dissipative electric field is generated. The stability break and the current sheet decay into a system of magnetohydrodynamic (MHD) waves. The topology of the magnetic field is changed, and the plasma is accelerated at slow shocks which correspond to, so-called, active or switch-on phase of reconnection. Then the magnetic field density decreases near the diffusion region, and eventually, the dissipative electric field is switched off. The region with accelerated plasma bounded by slow shocks (so-called, field reversal regions, FRRs or outflow regions) detach from the former site of diffusion and propagate in opposite direction along the current sheet (switch-off phase). It is commonly assumed that a general result of reconnection is the generation of a accelerated plasma flows, which transport energy and momentum along the current sheet [Vasylunas, 1975].

However, reconnection is a rather complicated process. It will be shown that besides the plasma jets, a special MHD wave is generated in the inflow region and propagates with the jets. This wave contains the amount of energy which is equal to twice of the kinetic energy of the accelerated plasma inside the FRR. A complex MHD object which consist of an outflow region and a special MHD wave is formed and transports both kinetic and magnetic energy but, as will be shown, no momentum.

2. Solution of Reconnection Problem

The reconnection problem for time-varying conditions is solved for the case of weak reconnection which implies that the dissipative electric field must be much less than the Alfvén electric field:

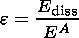(1)

At present it is not exactly known what kind of plasma instability is responsible for the generation of the reconnection electric field. Therefore it is convenient to prescribe the behavior of the electric field E _diss along a reconnection line a priori as a boundary condition rather than to calculate it from plasma theory.

The solution of the reconnection problem in an incompressible plasma in dimensionless form for the 2D symmetric configuration of magnetic field can be present as follows [Biernat et al., 1987; Semenov et al., 1985]

(2)

(3)

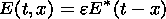(4)

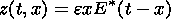(5)

where equation (2) are the components of the magnetic field, equation (3) is the velocity of the plasma, equation (4) is the electric field inside FRR, equation (5) is the shape of the shock wave and E^* is the electric field which is normalized to the maximum value of the dissipative electric field E _diss, so the E^* _max=1.

This solution in the outflow region does not look much more complicated than the original Petschek solution and in fact it can be reduced to the latter by the substitution E^*= const. Hence we can expect that the energy balance of the time-dependent reconnection might be very similar to the steady-state regime inside the outflow region. The main difference between steady-state and time-dependent conditions can bee seen in the inflow region where the magnetic field disturbances begin to play an important role:

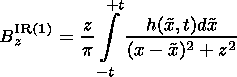(6)

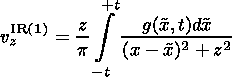(7)

(8)

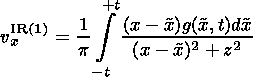(9)

The expressions for the first-order component of the magnetic field and the velocities of the plasma in the inflow region above and below current sheet are obtained from the Poisson integrals. Here h(x,t) is the first-order B_z component at the boundary of the outflow region and g(x,t) is the first-order v_z component at the same boundary, which is derived from the condition of the continuity of the normal component of the magnetic field B_n=0 and of the normal component of the velocity v_n - D_n=0, where D_n is the velocity of the shock:

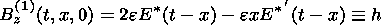(10)

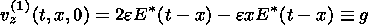(11)

All quantities are normalized to a magnetic field strength B₀, the velocity v_A=B₀/4pr, the characteristic duration of the reconnection pulse T₀, the length v_AT₀, and the energy density B₀²/8p. Because of symmetry, it is sufficient to consider all equations in the first quadrant only.

In the immediate vicinity of the reconnection line, x t,z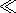 t, during the switch-on phase, this solution can be reduced to the well-known Petschek solution. The time-dependent solution is not much more complicated, but it can describe much more physics.

Different reconnection electric fields can be investigated in the framework of the time-dependent reconnection theory, such as burst-like, impulsive quasi-steady-state, etc. We will concentrate to the case of burst reconnection.

3. Energy and Momentum of the FRR

During the reconnection process, plasma is highly accelerated at the slow shocks and collected inside the FRRs so that the magnetic energy is converted into kinetic energy of the plasma. Taking into account that the kinetic energy density rv²/2 is normalized to the magnetic energy density B₀²/8p and in the dimensionless form is just v_v², we calculate the kinetic energy of the plasma in the FR region.

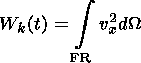(12)

where dW is the element of the volume.

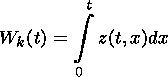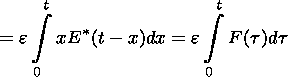(13)

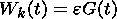(14)

where G(t) is the volume of the outflow region and F(t) is the reconnected magnetic flux:

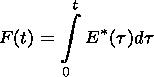(15)

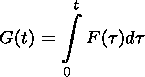(16)

Moreover, the FRR transports energy, mass, and momentum. The momentum of the accelerated plasma inside the FRR in dimensionless form can be calculated in a similar way:

(17)

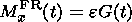(18)

All results are obtained for an arbitrary reconnection rate and because of that they are quite general, but to illustrate our conclusions, we model a pulse of reconnection by the following dissipative electric field:

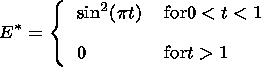(19)

Figure 2

It can be shown on Figure 2 that during the active phase of the reconnection when E^*>0 in the diffusion region, both the reconnected flux F(t) and the volume of the FRR G(t) rapidly increase. Hence magnetic energy is very rapidly converted into kinetic energy of the plasma at the shock, and the momentum of the plasma inside FRR rises as well. Then, during the switch-on phase when the electric field inside diffusion region becomes equal to zero, the volume of the outflow region G(t) increases further, whereas the amount of reconnection flux F(t) does not change any more. Although the dissipative electric field is switched off in the diffusion region, energy conversion still continues at the Petschek shocks, and as a result, the size of the outflow region normal to the current sheet linearly increases with time (see multiplier x in equation (5) of shocks). During this switch-off phase, FR regions detach from the reconnection line and propagate along the current sheet as solitary waves but not as a soliton. It is a fact that the kinetic energy and the momentum of the plasma inside the outflow region increase in time together with the volume because the shocks accelerate more and more plasma from the reconnected flux tubes. So, it can be shown that the volume of the FRR for large times t 1 is asymptotically

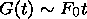(20)

where F₀ is the reconnected flux during the whole pulse of reconnection. Therefore G(t) is proportional to the distance from the former site of reconnection.

The total change of magnetic energy inside the FRR in dimensionless form is simply equal to

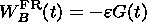(21)

So the kinetic energy of the plasma is equal to the decrease of energy of the magnetic field inside FRR. Thus, the magnetic field inside the FR region effectively disappears and the energy of the magnetic field in the outflow region is directly transformed into kinetic energy of the accelerated plasma so that the energy density in the FRR is conserved at each moment of time in every point.

It should be noted that this result follows just from the simple relation

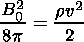(22)

which corresponds to the energy balance in the steady-state case.

Thus, the time-dependent regime of reconnection inside the outflow region is rather similar to the steady-state one. Magnetic energy is converted into kinetic energy with the efficiency coefficient to be equal to one (equation (22)). The only important difference between these two regimes is the switch-off phase which is essentially unsteady.

4. Energy Balance in the Inflow Region

Perturbation of the magnetic field and velocity in the inflow region are small (in first order with respect to e ), and therefore it can be supposed that the total energy of magnetic disturbances in the IR is also rather small. However, we have to take into account that although the inflow region is much less disturbed compared to the FRR, a bigger area is affected. Hence we have to make a more detailed analysis.

By definition, the total change of energy of the magnetic field in the inflow region is equal to

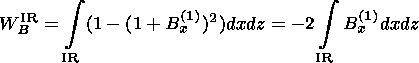(23)

It is advantageous to introduce a vector potential A so that

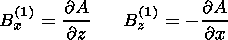(24)

with the gauge condition A(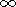)=0. Now we can integrate along the z axis in equation (23) to obtain

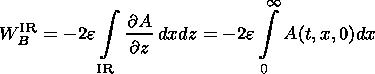(25)

Taking into account that the first-order component of the magnetic field at the boundary of the FRR is sufficiently simple (equation (10)), we can calculate the magnetic potential at the x axis:

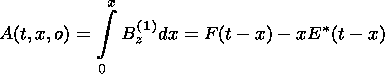(26)

Last, we obtain the following expression for the whole change of the magnetic energy in the inflow region:

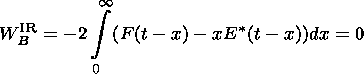(27)

The total change of the energy of the magnetic field in the IR turns out to be exactly zero. Hence it would be expected that the contribution of the magnetic disturbances to the energy balance is negligibly small in the inflow region, and energy conversion takes place only at shocks. However, in principal, there is still the possibility that positive and negative disturbances can compensate each other. Thus, it is necessary to analyze the behavior of the density of the magnetic field energy in different parts of the inflow region and to find the details of the energy distribution. By the variation of the limits of the integral (27) we can obtain the values of the change of the magnetic field energy at an arbitrary part of the IR.

The energy of magnetic disturbances in a column (x:[x,x+dx];z:[0,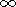)) is simply equal to (see equations (25) and (26))

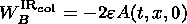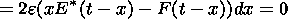(28)

Figure 3

The amount of the additional magnetic energy in the column is negative in the wake of the FRRs and positive above and below of the FR regions (Figure 3). It is also interesting to consider the function W_B ^IR(x) which is the energy of magnetic disturbances in the part of the IR defined by (x:[0,x];z:[0,)):

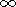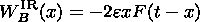(29)

This function linearly decreases from zero at the former site of reconnection to some minimum negative value near the position of the FRR and then increases to zero. This implies that the magnetic energy is negative for the wake of the field reversal regions and positive exactly in the column above the shocks. It should be emphasized that these positive and negative energies exactly compensate each other (see Figure 3).

From the physical point of view we can interpret this effect as follows. Fast moving shocks compress the magnetic field near their leading fronts and produce a compression wave. To some extent this is similar to the generation of a head wave from a fast moving boat on the water. Behind the moving FR regions the magnetic field becomes weaker than before reconnection, which leads to decrease of magnetic energy in the wake.

It can be shown that the amount of the positive energy in the compression wave is equal to

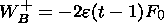(30)

Asymptotically, for t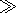1, the maximum value of this positive pulse is

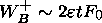(31)

which is double the kinetic energy W_k ^FR of the accelerated plasma in the FRR equation (14) at the same time t. This positive disturbed energy compensates exactly the smooth negative energy in the wake.

As a result, the energy balance in the inflow region can be described as follows. While the FRR propagates along the current sheet and collects all plasma from the reconnected magnetic flux tube, the magnetic field is compressed in the narrow vertical layer above and below the FRR and moves as a compression wave. It turns out that although the disturbances of the magnetic field in the inflow region are sufficiently small (order of e ), nevertheless, the total energy in the compression wave is approximately twice as big as the kinetic energy of a plasma jet. One can say that the efficiency coefficient of the reconnection process is equal to 1/2 in the sense that the generation of the plasma jet which transport some amount of the kinetic energy needs the double depletion of the magnetic energy in the wake.

5. Balance of Momentum During the Reconnection Process

It is generally believed that the outflow region can transport along the current sheet not only energy and flux but also momentum. As was shown, the moving FFR itself does transport momentum (equations (17) and (18)). On the other hand, we saw that the small disturbances in the inflow region can essentially contribute to the energy balance, and therefore we have to investigate details of momentum balance in the similar way.

Earlier it was supposed that the momentum of the system is conserved because there are two FRRs which move in opposite direction. However, besides of this, there are the plasma flows in the inflow region which have to transport momentum as well. A huge quantity of plasma is contained in the inflow region, and although the velocity of this plasma is less than the plasma jet velocity, it can be expected that the momentum of the IR is comparable with FRRs momentum.

For the investigation of the plasma flows in the inflow region the stream function is introduced:

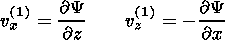(32)

The Y function can be calculate by means of the Poisson integral in the inflow region as a whole:

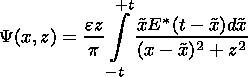(33)

Figure 4

The pattern of the stream lines Y= const is shown in Figure 4. As it can be seen, there is an inverse flow above the FRR and therefore this inverse flow contains negative momentum. Similar to the energy balance we can find x component of momentum of the plasma in the inflow region

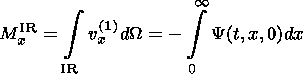(34)

In this case the stream function on the x line may be calculated using the equation for the first order component of the plasma velocity at the boundary of the FRR (equation (11))

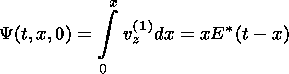(35)

Now we can rewrite equation (34) as follows:

(36)

The expression under the integral is equal to zero everywhere except in the interval (x:[t-1,t]), that is, the region above the FRR. So, the part of the plasma in the vertical column above the FR region has only negative momentum. Bearing in mind that the momentum of the outflow region itself is equal to G(t) equation (18), it is clear that the momentum of the inverse flow in the IR exactly compensates the momentum of the plasma jet and this inverse flow is concentrated in the column above the FRR. Hence it turns out that the moving FR region together with the inverse flow outside does not transport any momentum at all. So, generally speaking, it is impossible to create a rocket using the reconnection process.

Figure 5

Deals of the momentum distribution in the inflow region can be described by the function M_x ^IR(x) which is the x component of momentum of the inverse flow in the part of the IR defined by (x:[0,x];z:[0,))

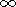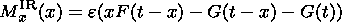(37)

From the first, this function is zero in the wake of the FRR, then it begins to increase and after that it stays constant. From Figure 5 one can see that the behavior of the x component of the momentum of the plasma jets and of the inflow region is identical. So, in consequence to the inverse flow, the momentum of the structure which consists of the outflow region and the compression wave is equal to zero, and this mean that this complex object transforms no momentum.

6. Energy Balance of Reconnection of Asymmetric and Skewed Magnetic Fields

In the case of the more realistic configurations of the initial magnetic fields [Kiendl et al., 1997; Rijnbeek et al., 1991] the energy and momentum balance are still similar to the simplest case.

Figure 6

The plasma accelerated at the slow shock is accumulated inside the FR regions. The FRRs propagate in opposite directions and transport kinetic energy which is equal to the reduction of the magnetic field energy in this regions. The compression wave is formed in the inflow region and contains essential the amount of the disturbed energy, leaving in the wake of the FRR a magnetic field which is slightly weaker than it was before reconnection (see Figure 6). These positive and negative parts compensate each other.

It should be emphasized that asymmetry decreases the amount of energy in the compression wave to a value of the kinetic energy of the plasma jets and changes the distribution of this energy between different parts of the wave. From the side of the bigger field the energy of magnetic disturbances is bigger than this energy from the other side.

A skew of the magnetic fluxes leads to increasing disturbed energy in the column above and below the FRRs. In this case, still more energy is contained in the compression wave, and therefore the loss of energy in the wake is more as well.

7. Conclusions

During the reconnection process the reconnection electric field, which is dissipative by nature, is transported through the current sheet via MHD waves and acts as a convective electric field there. As a result of that, a complex MHD object is formed. It consists of FRRs and special compression MHD wave, which transports no momentum and transfers both kinetic and magnetic energy.

Inside the field reversal region the magnetic energy is directly converted into kinetic energy of the plasma which is accelerated at the boundary of the FRR. The magnetic field reduction is balanced exactly by the kinetic plasma energy which is generated at the slow shock that can be expressed by the following relation:

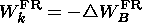(38)

Figure 7

In spite of the inflow region being much less disturbed, this region is far more extended, and this summary result turns out to be essential. So, a region with enhanced density of magnetic field energy is formed in the inflow region and propagates together with the FRR as the compression wave (see Figure 7). This wave contains an amount of energy which is equal to twice of the kinetic energy of the accelerated plasma inside the FRR. Simultaneously, this enhancement of magnetic energy in the compression wave is compensated by the rarefaction of the magnetic field and, as a consequence of that, by the decreasing of the density of magnetic field energy in the wake of the FRR:

(39)

In summary, the total energy budget of an elementary reconnection event behaves as follows: Inside the outflow region, there is a deficit of magnetic energy compensated by enhanced kinetic energy, leading to accelerated plasma jets. Outside the FRR, magnetic energy is accumulated ahead of the FRR as a result of its fast motion, leaving a rarefaction wake behind. After the generation of the plasma jets with some amount of kinetic energy the deficit of the magnetic field energy in the region between two FRRs proves to be double that of the kinetic energy.

The momentum of the accelerated plasma inside the FRR is exactly balanced by the momentum of sufficiently slow plasma inside the column above the FRR in the inflow region, so that the total momentum of the structure which consist of the plasma jets and the compression wave, is equal zero.

So, a complex object is formed as a result of reconnection. It transports no momentum and transfers both kinetic and magnetic field energy.

Acknowledgments

References

Biernat, H. K., Reconnection at the days magnetopause: Theory and comparison with data, Trends Geophys. Res., 535, 1993.

Biernat, H. K., M. F. Heyn, and V. S. Semenov, Unsteady Petschek reconnection, J. Geophys. Res, 92, 3392, 1987.

Coroniti, F. V., Explosive tail reconnection: the growth and expansive phases of magnetospheric substorm, J. Geophys. Res., 90, 7427, 1985.

Furth, H. P., J. Killen, and M. N. Rosenbluth, Finite-resistivity instabilities of a sheet pinch, Phys. Fluids, 6, 459, 1963.

Heyn, M. F., and V. S. Semenov, Rapid Reconnection in compressible plasma, Phys. Plasmas, 3, 2725, 1996.

Hones, E. W., Magnetic Reconnection in Space and Laboratory Plasmas, Geophysical Monogr. Ser., vol. 30, AGU, Washington, D.C., 1984.

Kiendl, M. T., V. S. Semenov, I. V. Kubyshkin, H. K. Biernat, R. P. Rijnbeek, and B. P. Besser, MHD analysis of Petschek-type reconnection in non-uniform field and flow geometries, Space Sci. Rev., 79, 709, 1997.

Ottaviani, P. L., and G. P. Porcell, Fast nonlinear magnetic reconnection, Phys. Plasmas, 2, 4104, 1995.

Parker, E. N., The solar flare phenomenon and the theory of reconnection and annihilation of magnetic fields, Astrophys. J. Suppl. Ser., 8, 177, 1963.

Petschek, H. E., Magnetic field annihilation, NASA Spec. Publ., SP-50, pp. 425-439, 1964.

Priest, E. R., The magnetohydrodynamics of current sheets, Rep. Progr. Phys., 48, 955, 1985.

Rijnbeek, R. P., V. S. Semenov, A. A. Shmaltc, H. K. Biernat, M. F. Heyn, and B. P. Besser, Time-dependent reconnection in a current sheet with a velocity shear Planet. Space Sci., 39, 1377, 1991.

Semenov, V. S., M. F. Heyn, and I. V. Kubyshkin, Reconnection of magnetic field lines in a nonstationary case, Sov. Astron. (in Russian), 27, 660, 1985.

Semenov, V. S., I. V. Kubyshkin, V. V. Lebedeva, R. P. Rijnbeek, M. F. Heyn, H. K. Biernat, and C. J. Farrugia, A comparison and review of steady-state and time-varying reconnection, Planet. Space Sci., 40, 63, 1992.

Sweet, P. A., The neutral point theory of solar flares, in Electromagnetic Phenomena in Cosmic Physics, edited by B. Lehnert, pp. 123-129, Cambridge Univ. Press, New York, 1958.

Vasyliunas, V. M., Theoretical models of magnetic field line merging, Rev. Geophys., 13, 303, 1975.