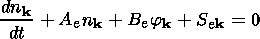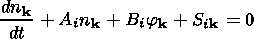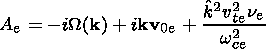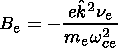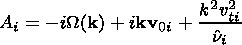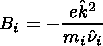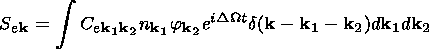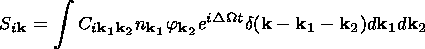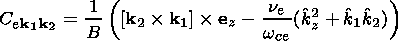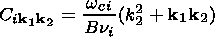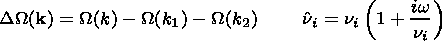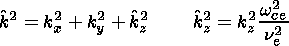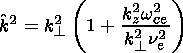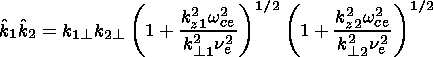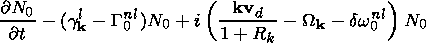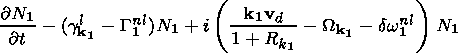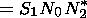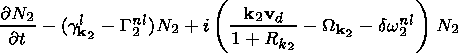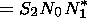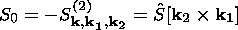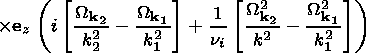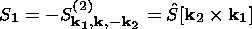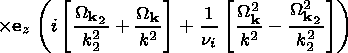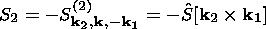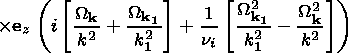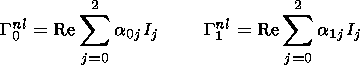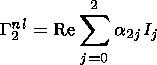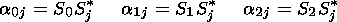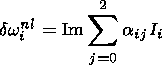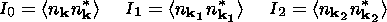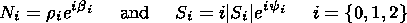k,
k1,
k2 is written in the form
[Tsytovich, 1970, 1971;
Weiland and Wilhelmsson, 1977]
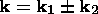 | (2) |
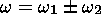 | (3) |
In the case of two-dimensional interaction of three waves
( k,j),
( k1,j1),
( k2,j)2,
from (2) follows
[Volosevich et al., 1982]
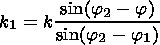 | (4) |
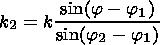 | (5) |
If one takes into account the weak dispersion of FB waves, one finds
in the case
j=0 from
(4) and (5) and the condition
w=w1+w2 that
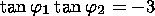 | (6) |
The physical sense of the last relation lies in the
fact that if two waves
in the stage of linear generation with
j=0 and
j1<10o act via decay
interaction, then the third wave must be
in the region of linear damping with
j2 p/2.
p/2.
Considering the system of equations consisting of the continuity equations
of the particles, the
MHD momentum balances
and the Poisson equation for the electric field, neglecting in
the electron momentum balance the inertial term, assuming quasineutrality
ne=ni=n, and assuming potential
electric field fluctuations with small amplitude
E=-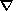 j,
one has for the time derivatives of the high-frequency density variations
[Volosevich and Meister, 2000a;
Volosevich et al., 1982]
j,
one has for the time derivatives of the high-frequency density variations
[Volosevich and Meister, 2000a;
Volosevich et al., 1982]
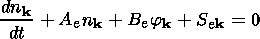 | (7) |
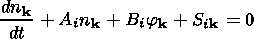 | (8) |
Here
nk=N/N0.
n k and
j k are the disturbances
of the density of the charged particles and the electrostatic potential.
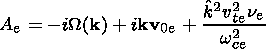 | (9) |
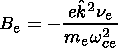 | (10) |
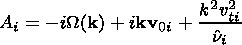 | (11) |
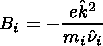 | (12) |
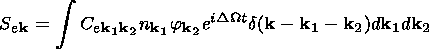 | (13) |
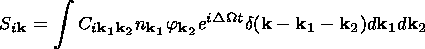 | (14) |
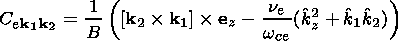 | (15) |
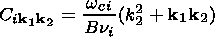 | (16) |
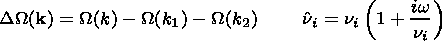 | (17) |
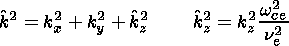 | (18) |
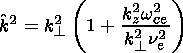 | (19) |
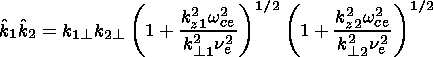 | (20) |
W( k) is the frequency of the density variations
with large
time scales,
d( k- k1- k2)
is the delta function, and
v0e and
v0i are the electron and ion drift velocities
that are determined by the mean electrostatic field
E0.
Se k and
Si k are the coefficients of the nonlinear
wave interaction of F-B waves.
Within the linear theory,
Se k and
Si k equal zero.
Then
j k is proportional to
n k. From (7) and (8)
follows
 | (21) |
Further, substituting (21) into (13) and (14),
the interaction coefficient of
second order with respect to the
nonlinear contributions
S(2) k, k1, k2 is found,
and so on.
S(2) k, k1, k2 coincide
with coefficients for decay processes given by
Tsytovich [1970, 1971]
and with coefficients occurring within the synchronism conditions
of nonlinear optics. Results
obtained in third order with respect to nonlinearity are presented in
Volosevich and Meister [2000b].
Substituting (21) in (7) and (8) and
taking
S(2) and
S(3) in (7) and (8) into account,
the expressions for the amplitudes of the waves in third order with respect
to the nonlinearity read
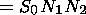 | (22) |
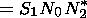 | (23) |
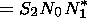 | (24) |
Here, one has
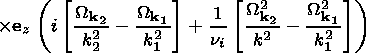 | (25) |
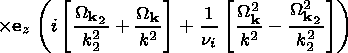 | (26) |
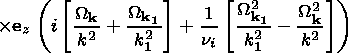 | (27) |
where
Nj=nkj/n0 are
disturbances of the density of charged particles due to
the waves number
j ( j=0,1,2 ).
gl kj
and
Gnlj designate
the linear and nonlinear increments of the interacting waves,
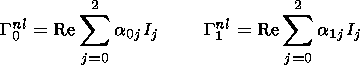 | (28) |
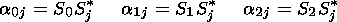 | (29) |
and
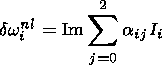 | (30) |
is the nonlinear frequency shift,
vd= v0e- v0i,
Wkj is the frequency of the
density variations,
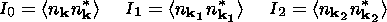 | (31) |
The system (22)-(24) describes the interaction of four waves.
In the relations (22)-(24), one sees the coefficients
S(2) and not
S(3), which describes the interaction of four waves (the moment
of
the fourth wave may be expressed by the momenta of the first
three waves using the momentum balance of four coherent waves).
Instead of
S(3),
Gnl k and
dw0nl
occur.
Thus, the physical sense of the system (22)-(24) consists in the fact
that, taking into account nonlinear effects of third order,
the nonlinear wave interaction causes a nonlinear contribution to the
growth rate and a nonlinear frequency shift. These phenomena result in the
stabilization of the instability.
Further,
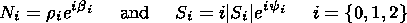 | (32) |
are supposed, and the set of equations (22)-(24) is divided into real
and imaginary expressions.
In the case of the low-frequency waves with
w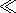 ni,
Re
Si
ni,
Re
Si
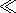 Im
Si, the main effect
of the wave interaction is the nonlinear phase shift.
But for the high-frequency waves with
w>ni
and
Re
Si
Im
Si, the main effect
of the wave interaction is the nonlinear phase shift.
But for the high-frequency waves with
w>ni
and
Re
Si
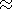 Im
Si,
nonlinear frequency shift and nonlinear contributions to the growth rate
are of importance, and these nonlinear effects lead to the stabilization
of the instability.
Im
Si,
nonlinear frequency shift and nonlinear contributions to the growth rate
are of importance, and these nonlinear effects lead to the stabilization
of the instability.
The system of equations (22)-(24) was solved numerically using the
Runge-Kutta method and considering initial conditions near stable states.
Applications were done for conditions with an unstable high-frequency
wave
(gl0>0), and two other
linearly damped waves
(gl1,gl2<0)
("large aspect angle" or "large flow angle").
|
|
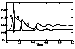
Figure 1
|
|
|
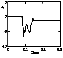
Figure 2
|

|
|
Figure 3
|
Examples of the numerical solution of (22)-(24) are presented in
Figures 1,
2,
3,
4,
and 5. Figure 1 shows the temporal evolution of the
relative amplitudes
r0,
r1,
r2 of the density
waves with
j=0;1;2 with respect to the background density for
k=5 m-1
(in Figure 5,
k=1 m
-1 is considered). The
time,
t, is measured in seconds. In the initial state at
t=0,
the high-frequency wave
j=0 is unstable and the low-frequency
wave
j=2 is damped as
j2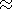 p/2. If
r1 and
r2 are small, the amplitude
r0 grows exponentially.
But with the time, if the amplitude
r0 will be large enough,
the amplitudes
r1 and
r2
also increase by nonlinear interaction.
The amplitude of the linearly damped wave 2 and
the relative phase of the waves
q=b1+b2-b0
are shown
in Figures 2
and 3,
respectively. Nonlinear stabilization occurs if the
time
of the linear increase of the amplitude
r0 of the unstable wave
1/gl0 is smaller
than the time of the nonlinear interaction
tnl. In the contrary case, the
explosive instability may be excited.
p/2. If
r1 and
r2 are small, the amplitude
r0 grows exponentially.
But with the time, if the amplitude
r0 will be large enough,
the amplitudes
r1 and
r2
also increase by nonlinear interaction.
The amplitude of the linearly damped wave 2 and
the relative phase of the waves
q=b1+b2-b0
are shown
in Figures 2
and 3,
respectively. Nonlinear stabilization occurs if the
time
of the linear increase of the amplitude
r0 of the unstable wave
1/gl0 is smaller
than the time of the nonlinear interaction
tnl. In the contrary case, the
explosive instability may be excited.
From Figures 1,
2, and
3 follows, that under the condition that the initial relative
amplitudes of the waves are small (about
10-3 ), then, for some time,
the
amplitude of the linearly unstable wave grows, and the amplitudes of the
initially damped waves are small. But, if the amplitude of the unstable
wave has grown up to a sufficient level, the nonlinear interaction results
in an increase
of the amplitudes of modes 1 and 2. This process leads to a
quasi-stabilized state, the amplitudes of the interacting waves
behave almost periodically, and the relative phase
q approaches a constant value. When the quasi-periodic
state is established,
the amplitudes of the initially linearly damped waves are larger
than the amplitude of the initially linearly growing wave.
The stabilization of the waves at a finite amplitude is accomplished
by modifying of the linear growth rate. It depends on the
average wave fluctuation level and lasts until the nonlinear
growth rate balances the linear growth rate.

|
|
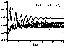
Figure 4
|
|
|
Figure 5
|
The numerical simulations for large intervals
of the parameters of the interacting waves showed that the solving the
system of equations (22)-(24) depends on the wave parameters and the
parameters of the ionosphere. The solution may be stationary, periodic,
multi-periodic,
quasi-stochastic, and stochastic.
In Figure 4,
results for the nonlinear interaction of waves with strong decay
of the waves
j=1, 2 are presented. In such a case, the solution is similar
to a stochastic one
[Vysshkind and Rabinovich, 1976;
Wersinger et al., 1980].
It depends on the initial conditions
and the relative phase
q of the waves' increases slowly with the time.
3. Conclusions
The nonlinear interaction between high-frequency and low-frequency
modes, excited by the
FB instability
in the collisional ionospheric
E region during the linear
stage of wave generation,
is considered within the frame of MHD.
Taking the
MHD system of equation
contributions of third order with respect to the nonlinearity
into account, a self-consistent system of equations
for the amplitudes and phases of three interacting waves is derived.
The results of the numerical solution
of the system of equations allows us to make the following conclusions:
1. If in the ionospheric plasma FB waves with linearly
increasing amplitudes exist, then the most
intensive wave interaction occurs in the propagation cone around the
electron drift velocity with an angle of about
j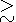 arccos
v0e/cs ( v0e is the electron drift
velocity,
cs represents the sound velocity).
The wave interaction results in the generation of rather intensive waves
that propagate perpendicularly to the electron drift velocity.
arccos
v0e/cs ( v0e is the electron drift
velocity,
cs represents the sound velocity).
The wave interaction results in the generation of rather intensive waves
that propagate perpendicularly to the electron drift velocity.
2. If the plasma system is in the weakly supercritical regime
with electron drift velocities of the order of 1.1 sound velocities,
the explosive instability may also occur.
This
means
that,
under such conditions,
the interaction of four waves is not effective. With increasing level
of supercriticality, the effectiveness
of the three- and four-wave interactions
grows.
3. If the case that the previously linear waves have wavelengths of the
order of 1-5 m,
the amplitudes of the waves beyond the linear region of evolution are of the
order of 6% of the mean density,
and the amplitudes of the nonlinear waves increase with increasing
wavelength of the plasma disturbances and with growing electron drift
velocity.
4. The nonlinear evolution of FB waves by coherent wave
interaction can result in states of different types:
quasi-stationary states for interacting low-frequency waves, periodic and
multi-periodic behavior for high-frequency waves with
w>ni
(Figures 1,
2, and
3), and quasi-stochastic behavior (Figure 4).
The
evolution
scenario
depends on the plasma parameters ( ne,
ni,
Te,
Ti,
v0e ) and on the parameters of the interacting waves
(the frequencies
and growth rates as well as the ranges
of the aspect and flow angles and the frequency of the unstable waves).
5. The
results
obtained
may be used to interpret
experimental data obtained during auroral radioscatter experiments.
Acknowledgments
A.V.V. thanks the organization Deutsche
Forschungsgemeinschaft for financial support within the frame of
contract WER 17/2/00 and the Fund of Fundamental Research of the Belarus
Republic, project F-378.
C.-V.M. gratefully thanks the Ministerium fur
Wissenschaft, Forschung und Kultur des Landes Brandenburg for
financial support by the HSP-3 project 24-04/055;2000.
References
Fedorov, V. P., M. G. Gelberg, and A. V. Volosevich,
A simulation of the evolution of low-frequency plasma turbulence
in the ionospheric
E region,
in Ionospheric Response in the Solar Wind,
edited by L. Triskova, Prague, 1988.
Gershman, B. N., L. M. Erukhimov, and Yu. Ya. Yashin,
Wave Phenomena in the Ionosphere (in Russian), Nauka, Moscow, 1984.
Hamza, A. M., and J.-P. St.-Maurice,
A self-consistent fully turbulent theory of auroral
E region irregularities,
J. Geophys. Res., 98, 11,601, 1993.
Hamza, A. M., and J.-P. St.-Maurice,
Large aspect angles in auroral
E region echoes. A self-consistent turbulent theory,
J. Geophys. Res., 100 (A4), 5723, 1995.
Janhunen, P., Perpendicular particle simulation
of the
E region Farley-Buneman instability,
J. Geophys. Res., 99 (A6), 11,461, 1994.
Lee, K., C. F. Kennel, and I. M. Kindel,
High frequency Hall current instability,
Radio Sci., 6, 209, 1971.
Liperovsky, V. A., C.-V. Meister, S. A. Senchenkov,
K. V. Popov, M. A. Oleynik, and E. V. Liperovskaya,
Consequences of current generation in the ionosphere caused by neutral
wind action on
Es clouds,
Izv. Vuz. Radiofiz. (in Russian), 39 (2), 241, 1996.
Meister, C.-V., Farley-Buneman type waves caused by the influence
of neutral winds on sporadic
E layers,
Abstr. Ser. German Astron. Soc., 11, 293, 1995.
Newman, A. L., and E. Ott, Nonlinear simulations of type 1
irregularities in the equatorial electrojet,
J. Geophys. Res., 86, 6879, 1981.
Oppenheim, M., and N. Otani,
Saturation of the Farley-Buneman instability
via nonlinear
E B drift instability,
J. Geophys. Res., 101 (A8), 17,273, 1996.
B drift instability,
J. Geophys. Res., 101 (A8), 17,273, 1996.
Otani, N., and M. Oppenheim,
A saturation mechanism for the Farley-Buneman instability,
Geophys. Res. Lett., 35 (11), 1833, 1998.
Robinson, T. R., and F. Honary,
A resonance broadening kinetic theory of the modified two-stream instability:
Implications for radar auroral backscatter experiments,
J. Geophys. Res., 95, 1073, 1990.
Sahr, J. D., and B. G. Fejer,
Auroral electrojet plasma irregularity theory and experiment:
a critical review of present understanding and future directions,
J. Geophys. Res., 101, 26,893, 1996.
Schlegel, K., and H. Thiemann,
Particle-in-cell plasma simulations of the modified two-stream instability,
Ann. Geophys., 12, 1091, 1994.
Sudan, R. N.,
Nonlinear theory of type I irregularities in the equatorial electrojet,
Geophys. Res. Lett., 10, 983, 1983.
Tsytovich, V. N., Nonlinear Effects in Plasmas, Plenum Press,
New-York, 1970.
Tsytovich, V. N., Theory of Turbulent Plasmas (in Russian),
Gozatomizdat, Moscow, 1971.
Uspensky, M. V., et al.,
Auroral radar backscatter at off-perpendicular
aspect-angles due to enhanced
ionospheric refraction,
J. Geophys. Res., 99, 17,503, 1994.
Volosevich, A. V.,
Farley-Buneman instability in the polar ionosphere,
in Phenomena in the Polar Ionosphere (in Russian),
Nauka, Leningrad,
1978.
Volosevich, A. V., and Y. I. Galperin,
Nonlinear wave structures in collisional plasma of auroral
E region
ionosphere, Ann. Geophys., 15, 899, 1997.
Volosevich, A. V., and V. A. Liperovsky,
Generation of small-scale ingomogenities
in a turbulent plasma and radio aurora,
Geomagn. Aeron. (in Russian), 15 (1), 74, 1975
Volosevich, A. V., and C.-V. Meister, Coherent three-wave interaction
in the ionospheric plasma,
Vestnik MG (in Russian), No. 6, edited by M. A. Avlasevich,
Mogilev State University,
Mogilev, Belarus,
2000a.
Volosevich, A. V., and C.-V. Meister,
Nonlinear coherent four-wave interaction in space plasma,
Astron. Nachr., 321, 263, 2000b.
Volosevich, A. V., V. A. Liperovsky, and M. A. Lifshits,
Nonlinear mechanism of the stabilization of the Buneman-Farley instability,
in Research of the High-Latitudinal Ionosphere and Magnetosphere (in Russian),
Nauka, Leningrad,
1982.
Vysshkind, S. Y., and M. I. Rabinovich,
The phase stochastization mechanism and structure of wave turbulence in
dissipative media,
Sov. Phys. JETP, 71 (218), 557, 1976.
Weiland, J., and H. Wilhelmsson,
Coherent Nonlinear Interaction of Waves in Plasmas,
Pergamon Press, New-York, 1977.
Wersinger, J.-M., J. M. Finn, and E. Ott,
Bifurcation and "strange"
behavior in instability saturation by nonlinear
three-wave mode coupling,
Phys. Fluids, 23 (3), 1142, 1980.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on December 8, 2002.
 wce, and non-magnetized ions,
ni
wce, and non-magnetized ions,
ni wci, ( ne,
ni are the collision frequencies
of the electrons and the ions with the neutral particles;
wce,
wci designate the electron and
ion gyrofrequencies),
the FB instability may occur in the presence of electrostatic fields.
The dispersion equation of linearly growing waves with frequency
w<ne,ni reads
[Volosevich and Galperin, 1997]
wci, ( ne,
ni are the collision frequencies
of the electrons and the ions with the neutral particles;
wce,
wci designate the electron and
ion gyrofrequencies),
the FB instability may occur in the presence of electrostatic fields.
The dispersion equation of linearly growing waves with frequency
w<ne,ni reads
[Volosevich and Galperin, 1997]
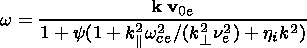
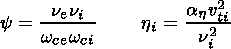
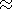 100 km above the surface of the
Earth, at
which
ni
100 km above the surface of the
Earth, at
which
ni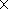 103 s
-1 and
v0e
103 s
-1 and
v0e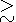 ne
are also possible. In the works
[Lee et al.,
ne
are also possible. In the works
[Lee et al., 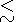 k
k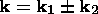
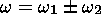
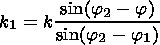
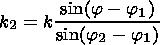
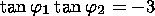
 p/2.
p/2.
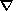 j,
one has for the time derivatives of the high-frequency density variations
[Volosevich and Meister,
j,
one has for the time derivatives of the high-frequency density variations
[Volosevich and Meister,