 1-10 kV.
At the same altitudes, perpendicular spatial scales of about 100 km are
most typical for the parallel electric fields
[Gorney, 1984].
Besides,
finer scales have been observed inside the larger features.
1-10 kV.
At the same altitudes, perpendicular spatial scales of about 100 km are
most typical for the parallel electric fields
[Gorney, 1984].
Besides,
finer scales have been observed inside the larger features.
V. E. Zakharov
Department of Physics, Kaliningrad State University, Russia
C.-V. Meister
Potsdam Astrophysical Institute, Germany
As known, both the magnetic field and the plasma of the magnetosphere are non-uniform. The pressure gradients of the plasma are caused by the electromotive force that produces electric currents in the magnetosphere. The ionosphere is the resistivity load connected to the magnetospheric sources of electric power via highly conducting magnetic field lines. The magnetospheric and ionospheric current system is closed by the field-aligned electric currents (FAC).
Kindel and Kennel [1971] suggested that electrostatic ion-cyclotron (EIC) waves could be produced by FAC. The EIC waves are usually found in regions with upgoing ion beams [André et al., 1987]. EIC waves have spectral peaks above the ion gyrofrequencies and sometimes at higher harmonics.
Waves also may be essential for the formation of a quasi-static difference of the electric potential V along the magnetic field lines. Microinstabilities cause anomalous resistivity in the plasma and the appearance of the electric fields E|| parallel to B [Lysak and Dum, 1983]. A second generation mechanism of these fields is based on a local charge separation in the FAC regions, where electrostatic double layers occur [Block, 1975; Block and Fälthammar, 1991]. Both generation mechanisms do not exclude one another; instead, they complement one another. Hesse et al. [1990] considered both mechanisms, applying the resistive fluid theory to the field-aligned potential structures.
Auroral arcs may be present because the parallel electric fields
accelerate the auroral electrons downward
[Chiu and Cornwall, 1980].
Strong electric spikes of about 100 mV m-1 were locally detected by
the Freja satellite
[Chust et al., 1988].
Using the results of
observations obtained by polar orbiting satellites, it was shown that
the potential differences are usually located at altitudes between
2000 and 15,000 km
[Reiff et al., 1988, 1993].
Reiff et al. [1993]
also
estimated that the
potential differences may be as large as
DV  1-10 kV.
At the same altitudes, perpendicular spatial scales of about 100 km are
most typical for the parallel electric fields
[Gorney, 1984].
Besides,
finer scales have been observed inside the larger features.
1-10 kV.
At the same altitudes, perpendicular spatial scales of about 100 km are
most typical for the parallel electric fields
[Gorney, 1984].
Besides,
finer scales have been observed inside the larger features.
The electric component of the electromagnetic waves, if it is parallel to the geomagnetic field B, modulates the field-aligned fluxes of the electrons at the wave frequency. In the case of electromagnetic ion-cyclotron (EMIC) waves, the modulation effect has been detected by sounding rockets [Lund and LaBelle, 1997; Temerin et al., 1993]. Erlandson et al. [1994] observed the EMIC waves by Freja satellite in a region of inverted V-type electron precipitation. Using simultaneous Freja observations of precipitating keV electrons and EMIC waves, Oscarsson et al. [1997] concluded that the EMIC wave-particle interaction is resonant at altitudes of several thousands of kilometers above the auroral ionosphere.
Growth and damping of the oblique EMIC waves were studied by Xue et al. [1996] for the conditions of the Earth's outer magnetosphere ( L=7, where L is the geomagnetic shell parameter) when the energetic particle distribution has a high-energy tail that may be modeled by a generalized Lorentzian distribution. The maximum wave growth due to hot proton temperature anisotropy was found to occur for the parallel wave propagation.
Chaston et al. [1999] discussed the observations of electromagnetic bursts in the near-Earth magnetotail by ISEE 1 and ISEE 2. Since the frequency range of the observed waves contains the cyclotron frequencies of the ion components found in this region of space, they loosely term these bursts "electromagnetic ion-cyclotron waves.'' The polarized bursts are often accompanied by anisotropic ion distributions and/or significant field-aligned currents. The character of the polarized events is different than that of the largely unpolarized/incoherent activity. As reported by Bauer et al. [1995], the energetic spectrum of these bursts does not exhibit any structure near the ion gyrofrequencies. The measured wave amplitude of the bursty polarized activity may be significantly larger than that of the unpolarized activity over the same frequency band [Chaston et al., 1999].
Several distribution functions of energetic electrons observed in the topside auroral ionosphere cannot result only from acceleration by a quasi-static electric potential drop, causing only a primary electron beam [Lynch et al., 1994]. The bursts of downgoing, field-aligned electrons may be generated by waves and can subsequently generate other waves.
The term "broadband extremely low frequency (BB-ELF) waves'' refers to the electric field fluctuations in the range 10 Hz to 3 kHz observed in the auroral ionosphere by sounding rockets and satellites at altitudes in the range 850-1700 km [André et al., 1998; Kintner et al., 1996]. It was found that these fluctuations are gyroresonant with the unheated ionospheric ion population. A comparison was made between space relevant observational signatures, such as frequency, spectra, phase velocities, excitation thresholds, and ion heating, and those signatures associated with EIC waves excited in a laboratory experiment [Koepke et al., 1999]. It was concluded that the observed BB-ELF waves may be excited by a plasma instability related to inhomogeneity in the perpendicular plasma flow in the presence of parallel current.
This study considers the wave characteristics and generation mechanisms of both quasi-stationary electrostatic ion-cyclotron turbulence and bursts of polarized transverse electromagnetic waves at frequencies close to the proton gyrofrequency. The first purpose of this work is to investigate transport and energization of both the thermal and auroral plasma in the presence of quasi-stationary, current-driven EIC turbulence in the magnetosphere. In a self-consistent way, this is done numerically in dependence on the FAC intensity, the thickness of the turbulent region, and the intensities of the EIC waves and magnetospheric convection, respectively. Second, the dispersion relation of electromagnetic waves in anisotropic convecting plasma will be obtained. Third, the behavior of the wave vector and increment of wave growth will be estimated in dependence on the frequency and polarization of the waves.
A closed magnetic flux tube is given in the auroral magnetosphere. To describe this flux tube, the empirical model of the magnetospheric field presented by Tsyganenko [1995] is used. The behavior of the anisotropic plasma is described by the system of MHD equations. Additionally, the dispersion equation of the EIC waves [Lominadze and Stepanov, 1984] and an equation for the balance between growth and damping rates of the waves are taken into account. To describe anomalous transport of the thermal and auroral plasma, we use the model equations presented by Zakharov and Meister [1999].
In our model, the magnetospheric plasma consists
of four components. They are the thermal protons ( j=1 ) and electrons
( j=2 )
as well as the auroral protons ( j=3 ) and electrons ( j=4 ).
nj,
vj,
T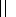 j, and
T
j, and
T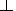 j designate particle
density, mean velocity, and the parallel and
perpendicular temperature components of the plasma, respectively.
The plasma obeys
the condition of quasi-neutrality
j designate particle
density, mean velocity, and the parallel and
perpendicular temperature components of the plasma, respectively.
The plasma obeys
the condition of quasi-neutrality
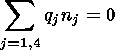 | (1) |
where qj is the electric charge per particle.
The velocity equals
vj= v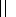 j+ v
j+ v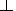 j
where
v
j
where
v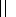 j and
v
j and
v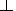 j are the parallel
and
perpendicular components of
vj, respectively.
Taking the electric, curvature, and gradient drifts into account,
v
j are the parallel
and
perpendicular components of
vj, respectively.
Taking the electric, curvature, and gradient drifts into account,
v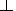 j may be approximated
by
[Goldstone and Rutherford, 1995]
j may be approximated
by
[Goldstone and Rutherford, 1995]
 |
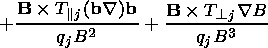 | (2) |
where
E is the total strength of the electric field,
E=E||+E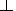 ,
E||
and
E
,
E||
and
E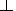 are the parallel and perpendicular components of
E.
E
are the parallel and perpendicular components of
E.
E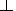 is caused by magnetospheric convection, b is the unit vector directed along the
geomagnetic field B.
is caused by magnetospheric convection, b is the unit vector directed along the
geomagnetic field B.
The continuity and momentum equations of the anisotropic plasma are [Goldstone and Rutherford, 1995]
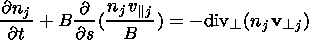 | (3) |
and
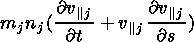 |
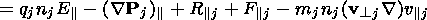 | (4) |
where
R j and
F
j and
F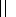 j are the parallel
components of the friction force caused by wave-particle
interaction and of the gravitational force per unit of volume,
respectively.
Tj designates the effective temperature of the
plasma defined by the expression
Tj=2T
j are the parallel
components of the friction force caused by wave-particle
interaction and of the gravitational force per unit of volume,
respectively.
Tj designates the effective temperature of the
plasma defined by the expression
Tj=2T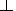 j/3+T
j/3+T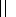 j/3. Thus, one obtains
j/3. Thus, one obtains
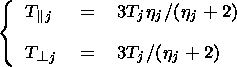 | (5) |
where
hj=T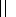 j/T
j/T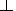 j.
j.
To calculate Tj, the following equation that describes the thermal balance of the plasma is used [Goldstone and Rutherford, 1995]
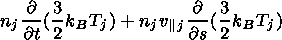 |
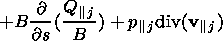 |
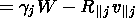 |
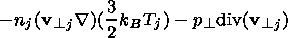 | (6) |
where
Q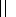 j is the thermal
flux density
caused by the thermal conductivity along
B,
Q
j is the thermal
flux density
caused by the thermal conductivity along
B,
Q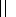 j=-kTj
j=-kTj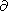 (kBTj)/
(kBTj)/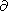 s,
kTj is the coefficient of thermal conductivity,
kTj=5njkBTj/(2mjnj),
nj is the collision frequency
of the particles scattered by the EIC waves,
gj is the growth
(or damping) rate of the EIC waves scattering the particles,
W is the
energy of the waves per unit of volume.
s,
kTj is the coefficient of thermal conductivity,
kTj=5njkBTj/(2mjnj),
nj is the collision frequency
of the particles scattered by the EIC waves,
gj is the growth
(or damping) rate of the EIC waves scattering the particles,
W is the
energy of the waves per unit of volume.
To apply the
Tsyganenko [1995]
model of the magnetospheric field,
the geophysical conditions of equinox and moderate geomagnetic
activity ( AE=50 ) are given. The solar-magnetic (SM) coordinate
system
(x,
y, z) is used to describe the magnetic field
[Sergeev and Tsyganenko, 1980].
The chosen magnetic field line
intersects the equatorial plane of the magnetosphere at the point
A(x=-8, y=-6) where
x and
y are expressed in units of the Earth radius
RE.
The length
s along
B is counted from the initial
point located at the altitude
h= hb=1000 km
in the southern hemisphere.
The given magnetic field line is situated inside a narrow flux tube;
the radius of the cross-section may be
estimated as
r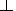 (s)=[F/(pB)]1/2
where
F is the magnetic
flux within this tube. The latter
is filled with turbulent plasma.
According to
Liperovsky and Pudovkin [1983],
satellite data averaged over
the
nightside auroral zone are used to describe the background
plasma located outside the turbulent region.
(s)=[F/(pB)]1/2
where
F is the magnetic
flux within this tube. The latter
is filled with turbulent plasma.
According to
Liperovsky and Pudovkin [1983],
satellite data averaged over
the
nightside auroral zone are used to describe the background
plasma located outside the turbulent region.
For the system of equations (1)-(6), the initial value problem is
considered. For each time step
Dt, the difference scheme
is applied based on the decomposition method
[Samarsky and Nikolaev, 1978].
The algorithm of decomposition consists of four
steps. At the first and second steps, only the effects of the
plasma transport along
Figures 1, 2, and 3 are obtained for the density
nj, the
temperature
Tj, and for the parallel flux density
njv
Profiles
are presented for
the plasma parameters and the parallel electric
field along one and the same magnetic field line in both the
southern and northern hemispheres.
The given
magnetic field line intersects the geomagnetic equatorial plane
at
s=sm
In our model, the value of the density of the electric current
j
The maximum value
DVm of the parallel difference
of the
electric potential
in one hemisphere (northern or southern) amounts to
DVm
The presence of the parallel electric field and the anomalous
resistivity cause an energization of the plasma. Under present
conditions, the thermal conductivity along
B and the
convection across
B effectively
prevent
heating
of the thermal plasma. In our model, the anomalous thermal
conductivity is absent in the auroral plasma as the wave-particle
interaction is negligible for this component of the plasma. The
pressure gradients of the auroral plasma along
B increase
while the intensity of the EIC waves becomes larger. The total
flux density of the electrons directed from the magnetosphere
into the ionosphere becomes larger while the strength of the
upward-directed field
E||
increases. Under the same
conditions, the field-aligned fluxes carried by the electrons are
much larger than those carried by the protons.
Figures 1, 2, 3, 4, 5, and 6 allows us to estimate how much the parallel electric
field
E||
may influence the profiles of
nj,
v|| j, and
Tj. For the thermal plasma, this influence is expected to
be
much more intensive than for the auroral plasma. This is so because,
with respect to the order of magnitude, the ratio
qjV/(kB Tj)
may be equal to
much larger values for
j=1, 2 than for
j=3, 4.
Due to magnetospheric convection, the colder (background) plasma
flows into the given flux tube. Then, the heated plasma leaves
this tube. The effectiveness of this loss depends strongly on the ratio
of the difference of the electric potential across the tube to the magnetic
flux
F of the same tube. While the ratio mentioned
above
becomes smaller, the temperatures of both protons and electrons
increase. After all, the thermal conductivity cannot prevent the plasma
from intensive heating
[Zakharov and Meister, 1999].
According to
Figure 5,
with respect to the order of magnitude,
the coefficient of thermal conductivity
of the electrons is about four orders larger than that of the protons.
For that reason, the ratio
T1/T2 rises
[Zakharov and Meister, 1999].
In such a case, the absolute values
of both
the increment
g1 and the decrement
g2 of the EIC waves
decrease. Thus, the EIC turbulence may be damped.
On the contrary,
when the flux tube becomes narrower, the convective heat loss
acts more effectively to prevent the plasma from
intensive heating. This is the case to which Figures 1-6
are
related.
The thermal conductivity of the plasma alone cannot prevent the
thermal plasma from intensive heating in thick magnetic flux
tubes when the convection is weak and the relative intensity of
the EIC turbulence amounts to
W/(n2kBT2)
As shown in Figure 5, the coefficient of thermal conductivity
kTj ( j=1, 2 ) has its largest values at high altitudes,
and it decreases when the observational point moves downward along
B.
This is so as the intensity of turbulence
W/(n2kBT2) decreases
while the observational point moves along
B toward higher
altitudes. Anomalous resistivity is only one
factor causing
the appearance of parallel electric fields in the auroral magnetosphere.
In our model, these fields may also be caused by polarization of both
the thermal and auroral plasma as well as by the presence of the component
of
the inertia force. Figure 6 shows that
the total parallel electric field
E||
is almost completely caused by anomalous
resistivity. When the
observational point moves along
B toward lower altitudes,
the values of
E||
driven by anomalous resistivity increase.
The derivation of the general dielectric tensor K for obliquely
propagating linear waves in a hot magnetized plasma has been carried out
by many authors
(e.g., Krall and Trivelpiece [1973]).
General expressions for the elements of the dielectric tensor for an
arbitrary particle
distribution function are given by
Summers et al. [1994].
Xue et al. [1996]
adopted these
expressions to describe EMIC waves in a plasma with temperature anisotropy.
Gary and Schriver [1987]
and
Summers and Thorne [1992]
worked out
the dispersion relations
for EMIC waves propagating
along B in a drifting plasma with temperature anisotropy.
Gary and Schriver [1987]
([Summers and Thorne, 1992])
supposed the
distribution functions of the plasma components to be Maxwellian
(Lorentzian).
In this section, the expressions evolved for K by
Gary and Schriver [1987]
and
Xue et al. [1996]
will be generalized.
To do this, the effects of the plasma drift will be additionally
taken into account for obliquely propagating waves.
We assume the plasma to be homogeneous, infinite, and immersed in a uniform
magnetic field pointing
in the
z -direction of a Cartesian coordinate system. We assume further
that perturbations about the zero-order
values of the particle distribution function and the electric and magnetic
fields are small, that
all perturbed quantities vary as
ei( k r-w' t)
where
k is the wave vector,
r is the radius-vector of the observational point,
w' is the
complex frequency of electromagnetic
oscillations,
w'=w+ig,
g is the wave growth
(damping) rate when
g>0 ( g<0 ),
and
t is the time. Without loss of generality, the wave vector
k may be written as
where
ex and
ez are the unit vectors of the coordinate
system, which are directed along the
x and
z coordinate axes, respectively,
k
We consider the case where the mean velocities of all components of the
plasma are directed along
B.
In particular, some of these velocities or all of them may be equal to zero.
By solving the Maxwell equations and the Vlasov equation, the following
dispersion relation may
be found for oblique waves in a hot magnetized plasma
where
n is the refractive index,
n=ck/w',
c is the velocity of
light,
l is the angle between the wave vector
k and the
z (or
magnetic field) direction,
Kab
are the components of the dielectric tensor
K, and
a={x,y,z},
b={x,y,z}.
The distribution of the convective anisotropic plasma may be described
by a bi-Maxwellian function shifted along the mean magnetic field
B=B ez
where
as and
a
We worked out that the components of the dielectric tensor
Kab
may be expressed by
where
wps
is the plasma frequency,
wps=
[ns qs
/ms e0)]1/2,
Ln= exp(-ns)
In(ns),
In is the modified Bessel
function of the first kind of order
n,
Z is the plasma dispersion function
[Summers et al., 1994],
s denotes the plasma component,
ms and
qs are
the mass and electric
charge per particle, respectively,
ns is the
partial density of the plasma,
e0 is the
dielectric susceptibility of the vacuum,
v|| and
v
In the case where
vDs=0, the expressions
(13)-(21) obtained by us
for the components of the dielectric tensor
K correspond to those presented by
Xue et al. [1996].
Xue et al. [1996]
investigated the dispersive properties of the EMIC
oblique waves below the proton
gyrofrequency
wc1, which are excited due to
the temperature
anisotropy of
energetic protons near the geomagnetic equator at
L=7 in the plasma sheet.
The effects of plasma drift were
not taken into account. It was found that
the EMIC waves may indeed be unstable under these conditions. The maximum
values of the wave growth rate
normalized by the proton gyrofrequency were estimated to be of the order of
g/wc1
Chaston et al. [1999]
considered EMIC waves propagating
along
B ( k
In this study, we investigate the growth and dispersion properties of
oblique ion-cyclotron waves with
frequencies close to the proton gyrofrequency. In the case where
|g/ wc1|
The expressions (13)-(21) obtained for the components
Kab
of the dielectric tensor
K are employed in (22)
and
(23).
The approximate dispersion relation (22) is solved numerically
using the trial method
[Korn and Korn, 1968].
To calculate the
perpendicular component
k
The numerical estimates show that the contributions of thermal plasma
to the components of the
dielectric tensor
K are about two orders of magnitude larger than
the contributions of the energetic plasma.
For that reason, the parameters are given only for the thermal plasma.
To guarantee the validity of (23), the calculations are only performed
for the narrow frequency bands close to the proton gyrofrequency, for which
|g/wc1|<1.
In the case of our calculations, the
FAC intensity amounts to
j||=2.0
Repeating the calculations for a different choice of
the observational point at the given magnetic field line, we find that the
plasma instability in the drifting magnetospheric plasma is not localized
at small altitudes ( h
It should be pointed out that numerical calculations were performed by us
not only for the right-hand,
but also for the left-hand polarized ion-cyclotron waves
( w< -wc1 ).
It is found that
the latter waves are also unstable under present conditions.
On the order of magnitude, the growth
rate of the left-hand polarized waves may reach the same values
as were obtained above for the
right-hand polarized waves.
A numerical solution of equations describing
the anomalous transport of anisotropic magnetized plasma is found,
and profiles of the parameters of the multi-component plasma and of the
parallel electric field along the magnetospheric field are considered.
Having solved the stationary system of equations in a previous
paper
[Zakharov and Meister, 1999],
the relaxation of the
turbulent plasma
and of the parallel electric fields and currents from an initial state
up to the stationary state are simulated numerically.
Thus, it is shown that stationary solutions indeed exist.
In this context, acceleration and heating are considered, comparing
the parameters of the turbulent plasma with those related to the background
plasma in the neighborhood of the turbulent region.
The analysis shows that the current-driven
EIC turbulence may cause the large-scale anomalous resistivity of the plasma
of the Earth's ionosphere.
The resonant wave-particle interaction is most effective for the
upward-directed FAC with a density of a few
10-6 A m
-2 at the
upper boundary of
the nightside auroral ionosphere ( h=1000 km).
As shown, anomalous resistivity is able to produce differences of the
electric potential along
B in one (northern or southern) hemisphere
of about a few kV.
The electron
thermal conductivity is calculated to be about three to four orders of
magnitude
larger than the proton thermal conductivity.
Electron thermal conductivity increases with altitude.
According to the results of numerical calculations presented by
Zakharov and Meister [1999],
magnetospheric convection and thermal conductivity
are found to be the effective mechanisms providing the heat loss from
the turbulent region. In the case of narrow magnetic flux tubes and
intensive magnetospheric convection, these mechanisms effectively
prevent the turbulent plasma from heating. In the case of thick magnetic
flux tubes and weak convection, the current-driven anomalous
resistivity results in significant heating of the plasma.
The ratio between the temperatures of protons and electrons
increases while the plasma is heated.
What is the relevance of the stationary solution in the sense of physics?
As is well known, within
MHDs,
FAC
disturbances
are
carried along the magnetic field lines by Alfvén
waves. The time of
propagation of Alfvén waves from the magnetosphere
into the ionosphere
depends on the geophysical conditions and, according to the estimates,
may be of the order of a few minutes. This is much less than the duration of
a typical magnetospheric substorm when intensive FACs evolve. The presence of
intensive FACs
may cause turbulence in the plasma. As is known from satellite experiments,
electromagnetic noise is permanently observed in the magnetosphere as a
large-scale phenomenon. Besides,
small-scale bursts of electromagnetic noise
are also observed.
It is obvious that the bursts correspond to an
unstable plasma. During bursts, the growth rate of electromagnetic noise
may be significantly higher than its damping rate.
Under such conditions,
one has to deal with a nonequilibrium state and, particularly, temperature
anisotropy may occur.
Thus,
the growth and dispersion properties of oblique
ion-cyclotron waves excited in a
drifting magnetized plasma are
also
investigated. The expressions evolved for
the components
Kab
of the dielectric tensor K of the anisotropic plasma
by
Gary and Schriver [1987]
and
Xue et al. [1996]
are generalized. To do this, the effects of
the plasma drift are also
taken into account for obliquely propagating waves.
The approximate dispersion relation (22)
is solved numerically for the geophysical conditions relevant to the region
of intensive FAC of
the auroral magnetosphere. The wave growth (or damping) rate
g is
calculated from (23).
It is found that the excited oblique ion-cyclotron waves may reveal the properties of
bursts of polarized transverse electromagnetic waves at frequencies near
the proton gyrofrequency.
The curves shown in Figure 7 are related to highly oblique ion-cyclotron waves.
The resonant character of interactions of charged particles via ion
cyclotron waves is confirmed by
the calculated dependence of the wave growth rate
g on the intensity
of FAC.
On the order of magnitude, the values of the wave growth rate
g calculated by us correspond to those obtained
for the drifting plasma of
the near-Earth tail by
Chaston et al. [1999].
On the other hand,
Xue et al. [1996]
found that the maximum
wave growth due to the hot proton temperature anisotropy near the
geomagnetic
equator at
L=7 is less by one to two orders of magnitude than that calculated
by us.
An extended but not localized region of the plasma instability is found
by numerical calculations; it stretches
in the auroral magnetosphere. The plasma instability is excited at lower
values of the wave number
k if the altitude becomes larger.
André, M., H. Koskinen, G. Gustafsson,
and R. Lundin,
Ion waves and upgoing ion beams observed by the Viking satellite,
Geophys. Res. Lett., 14, 463, 1987.
André, M., P. Norqvist, L. Anderson, L.
Eliasson, A. I. Eliasson,
L. Blomberg, R. E. Erlandson, and J. Waldemark,
Ion energization mechanisms at 1700 km in the auroral region,
J. Geophys. Res., 103, 4199, 1998.
Bauer, T. M., W. Baumjohann, R. A. Treumann, N. Sckopke,
and H. Lühr,
Low frequency waves in the near-Earth plasma sheet,
J. Geophys. Res., 100, 9605, 1995.
Block, L. P., Double layers,
in Physics of the Hot Plasma in the Magnetosphere, edited by B. Hultqvist
and L. Stenflo,
p. 229,
Plenum Press, New York,
1975.
Block, L. P., and C.-G. Fälthammar,
Characteristics of magnetic field-aligned electric fields in the auroral
acceleration region, in Auroral Physics,
edited by
C.-I. Meng,
M. I. Rycroft, and
L. A. Frank,
p. 109,
Cambridge University Press,
New York,
1991.
Chaston, C. C., Y. D. Hu, and B. J. Fraser,
Electromagnetic ion-cyclotron waves in the near-Earth magnetotail,
J. Geophys. Res., 104, 6953, 1999.
Chiu, T. T., and J. M. Cornwall,
Electrostatic model of a quiet auroral arc,
J. Geophys. Res, 85, 543, 1980.
Chust, T. R., P. Louarn, M. Volwerk, H. de Feraudy, J.-E. Wahlund,
and
B. Holback,
Electric fields with a large parallel component observed by
the Freja spacecraft: Artifacts or real signals,
J. Geophys. Res., 103, 215, 1998.
Erlandson, R. E., L. J. Zanetti, M. H. Acun a, A. I. Eriksson,
L. Eliasson, M. H. Boehm, and L. G. Blomberg,
Freja observations of electromagnetic ion-cyclotron ELF waves and
transverse oxygen ion acceleration on auroral field lines,
Geophys. Res. Lett., 21, 1855, 1994.
Gary, S. P., and D. Schriver,
The electromagnetic ion-cyclotron beam anisotropy instability,
Planet. Space Sci., 35, 51, 1987.
Goldstone, R. J., and P.-H. Rutherford,
Introduction to Plasma Physics,
Institute of Physics Publishing, Bristol, 1995.
Gorney, D. J., Potential structures and particle acceleration
on auroral field lines,
Adv. Space Res., 4, 499, 1984.
Hesse, M., J. Birn, and K. Schindler,
A self-consistent two-dimensional resistive fluid theory of field-aligned
potential structures including charge separation
and magnetic and velocity shear,
J. Geophys. Res., 95, 18,929, 1990.
Kindel, J. M., and C. F. Kennel,
Topside current instabilities,
J. Geophys. Res., 76, 3055, 1971.
Kintner, P. M., J. Bonnell, R. Arnoldy, K. Lynch,
C. Pollock, and T. Moore,
Transverse ion acceleration and plasma waves,
Geophys. Res. Lett., 23, 1873, 1996.
Koepke, M. E., J. J. Carroll, and M. M. Zintl,
Laboratory simulation of broadband ELF waves in the auroral ionosphere,
J. Geophys. Res., 104, 14,397, 1999.
Korn, G. A., and T. K. Korn,
Mathematical Handbook,
McGraw-Hill, New York, 1968.
Krall, N. A., and A. W. Trivelpiece,
Principles of Plasma Physics, McGraw-Hill, New York, 1973.
Liperovsky, V. A., and M. I. Pudovkin,
Anomalous Resistivity and Double Layers in the Magnetospheric Plasma (in Russian),
pp. 122-146, Nauka, Moscow, 1983.
Lominadze, D. G., and K. N. Stepanov,
Excitation of the low-frequency longitudinal oscillations in the
magnetized plasma,
J. Theor. Phys. (in Russian), 34, 1823, 1984.
Lund, E. J., and J. LaBelle, On the generation and propagation of auroral electromagnetic
ion-cyclotron waves,
J. Geophys. Res., 102, 17,241, 1997.
Lynch, K. A., R. L. Arnoldy, P. M. Kintner, and J. L. Vago,
Electron distribution function behavior during localized transverse
ion acceleration events in the topside ionosphere,
J. Geophys. Res., 99, 2227, 1994.
Lysak, R. L., and T. Dum,
Dynamics of magnetosphere-ionosphere coupling
including turbulent transport,
J. Geophys. Res., 88, 365, 1983.
Oscarsson, T., A. Vaivads, K. Rönnmark,
J. H. Clemmons,
H. de Feraudy,
and B. Holback,
Toward a consistent picture of the generation of electromagnetic
ion-cyclotron ELF waves on auroral field lines,
J. Geophys. Res., 102, 24,369, 1997.
Reiff, P. H., H. L. Collin, J. D. Craven, J. L. Burch,
J. D. Winningham, E. G. Shelley, L. A. Frank, and M. A. Friedman,
Determination of auroral electrostatic potentials using high-
and low-altitude particle distributions, J. Geophys. Res., 93,
7441, 1988.
Reiff, P. H., G. Lu, J. H. Burch, J. D. Winningham,
L. A. Frank,
J. D. Craven, W. K. Peterson, and R. A. Heelis,
On the high- and low-altitude limits of the auroral electric field region,
in Auroral Plasma Dynamics,
Geophys. Monogr. Ser., vol. 80,
edited by
R. L. Lysak,
p. 143,
AGU,
Washington, D.C.,
1993.
Sergeev, V. A., and N. A. Tsyganenko,
The Earth's Magnetosphere (in Russian),
Nauka, Moscow, 1980.
Samarsky, A. A., and E. C. Nikolaev,
Integration Methods for the Grid Equations (in Russian),
Nauka,
Moscow, 1978.
Summers, D., and R. M. Thorne,
A new tool for analyzing microinstabilities in space plasmas modeled by
a generalized Lorentzian (Kappa) distribution,
J. Geophys. Res., 97, 16,827, 1992.
Summers, D., S. Xue, and R. M. Thorne,
Calculation of the dielectric tensor for a generalized Lorentzian
(kappa)
distribution function,
Phys. Plasmas, 1, 2012, 1994.
Temerin, M., C. Carlson, and J. P. McFadden,
The acceleration of electrons by electromagnetic ion-cyclotron waves,
in Auroral Plasma Dynamics,
Geophys. Monogr. Ser.,
vol. 80,
edited by R. L. Lysak, pp. 155-167,
AGU,
Washington, D.C.,
1993.
Tsyganenko, N. A.,
Modeling the Earth's magnetospheric magnetic field confined within
a realistic magnetopause,
J. Geophys. Res., 100, 5599, 1995.
Xue, S., R. M. Thorne, and D. Summers,
Growth and damping of oblique electromagnetic ion-cyclotron waves
in the Earth's magnetosphere,
J. Geophys. Res., 101, 15,457,
1996.
Zakharov, V. E., and C.-V. Meister,
Current-driven plasma turbulence in a magnetic flux tube,
Astron. Nachr., 320, 425, 1999.
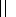 j and
gj W,
additionally the dispersion equation of the EIC waves and the
balance between growth and damping rates of the
waves are taken into account. The dependence between the plasma
and wave parameters is non-linear. Therefore, the iterations are
performed to calculate the parameters of the plasma and of the
EIC waves.
j and
gj W,
additionally the dispersion equation of the EIC waves and the
balance between growth and damping rates of the
waves are taken into account. The dependence between the plasma
and wave parameters is non-linear. Therefore, the iterations are
performed to calculate the parameters of the plasma and of the
EIC waves.
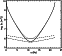
Figure 1

Figure 2

Figure 3
Figures 1,
2,
3,
4,
5,
and 6
show the results of the numerical calculations obtained
for the stationary state. There, profiles of the plasma
parameters and of the parallel electric field versus the length
s along the given magnetic field line are presented.
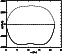
Figure 4
 j
of the plasma, respectively. Figure 4
represents the profiles of the ratio between the potential and
thermal energies per particle
qjV/(kBTj)
where
V is the
electric potential,
E=-
j
of the plasma, respectively. Figure 4
represents the profiles of the ratio between the potential and
thermal energies per particle
qjV/(kBTj)
where
V is the
electric potential,
E=-  V, and
V(s=0)=0.
V, and
V(s=0)=0.
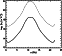
Figure 5
Figures 5 and 6 represent the profiles of the coefficient of thermal
conductivity
kTj and of the parallel electric field
E||,
respectively. In the latter case, both the total
strength
E||
and the contribution
-R|| 2/(q2n2)
due to the presence of the anomalous resistivity of
the plasma are shown.
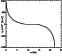
Figure 6
 11.2 RE.
11.2 RE.
 b flowing
from the magnetosphere into the ionosphere at
s=0 is not considered to be
constant.
Therefore, this value may be different in dependence on
the choice of the model parameters. For Figure 1, the current density is found
to be
j
b flowing
from the magnetosphere into the ionosphere at
s=0 is not considered to be
constant.
Therefore, this value may be different in dependence on
the choice of the model parameters. For Figure 1, the current density is found
to be
j b
b 3.1
3.1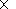 10-6 A m
-2.
10-6 A m
-2.
 1.2 kV.
1.2 kV.
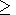 10-3 [Zakharov and Meister, 1999].
However, it may be that,
besides the EIC turbulence, other mechanisms provide greater
thermal conductivity.
10-3 [Zakharov and Meister, 1999].
However, it may be that,
besides the EIC turbulence, other mechanisms provide greater
thermal conductivity.
3. Modeling of Bursts of Obliquely Propagating EMIC
Waves

(7) 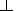 and
k are the
components of
k, which are
perpendicular and parallel to
B, respectively.
and
k are the
components of
k, which are
perpendicular and parallel to
B, respectively.
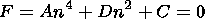
(8) 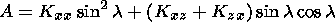
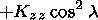
(9) 
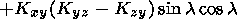

(10) 

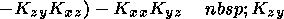
(11) 
(12) 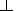 s
are the parallel and
perpendicular thermal velocities of
the plasma component
s,
a
s
are the parallel and
perpendicular thermal velocities of
the plasma component
s,
a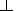 ,s=
(2kBT
,s=
(2kBT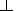 ,s/ ms)1/2,
and
kB is the Boltzmann constant.
,s/ ms)1/2,
and
kB is the Boltzmann constant.
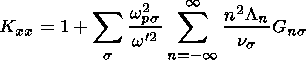
(13) 
(14) 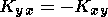
(15) 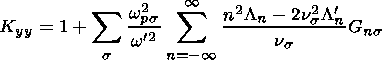
(16) 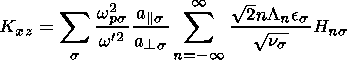
(17) 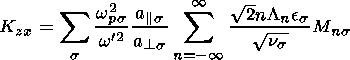
(18) 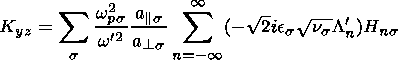
(19) 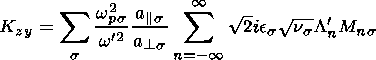
(20) 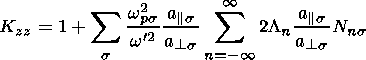
(21) 
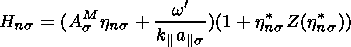
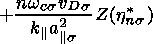
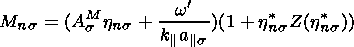


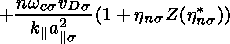
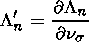
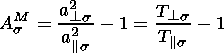
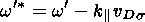
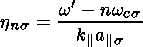
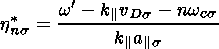
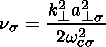
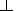 are the parallel and perpendicular
components of
the total velocity v
of a charged particle with respect to
B, respectively,
wcs
is the gyrofrequency of
a charged particle of the kind
s, and
wcs=
qsB/ms,
a|| s and
a
are the parallel and perpendicular
components of
the total velocity v
of a charged particle with respect to
B, respectively,
wcs
is the gyrofrequency of
a charged particle of the kind
s, and
wcs=
qsB/ms,
a|| s and
a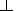 s
are the parallel and perpendicular
thermal velocities of
the plasma component
s,
a
s
are the parallel and perpendicular
thermal velocities of
the plasma component
s,
a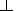 ,||s=
(2kBT
,||s=
(2kBT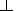 ,|| s/ms)1/2,
and
kB is the Boltzmann constant.
,|| s/ms)1/2,
and
kB is the Boltzmann constant.
 10-2.
10-2.
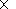 B=0 ) in the drifting
plasma of the
near-Earth magnetotail.
They showed that the influence
of heavy ions on wave growth and dispersion in the region of instability may
be ignored. They also demonstrated
that the properties of the instability remain almost the same as in the case
k
B=0 ) in the drifting
plasma of the
near-Earth magnetotail.
They showed that the influence
of heavy ions on wave growth and dispersion in the region of instability may
be ignored. They also demonstrated
that the properties of the instability remain almost the same as in the case
k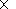 B=0 if
the angle between the wave vector
k and the direction of the main
magnetic field
B is less
than 45o. Taking the effects of the plasma drift into account and
solving the dispersion relation of
the EMIC waves,
Chaston et al. [1999]
estimated the maximum values of
g/wc1
to be of the order
of
10-1.
B=0 if
the angle between the wave vector
k and the direction of the main
magnetic field
B is less
than 45o. Taking the effects of the plasma drift into account and
solving the dispersion relation of
the EMIC waves,
Chaston et al. [1999]
estimated the maximum values of
g/wc1
to be of the order
of
10-1.
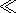 1,
the dispersion relation (8) may be approximated by
1,
the dispersion relation (8) may be approximated by
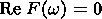
(22) 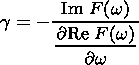
(23) 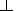 of
the wave vector
k, we specify the (real) values for the wave
frequency
w and the parallel component
k of the wave vector.
Then, the wave growth (or damping) rate
g is calculated from (23).
of
the wave vector
k, we specify the (real) values for the wave
frequency
w and the parallel component
k of the wave vector.
Then, the wave growth (or damping) rate
g is calculated from (23).
The results of the numerical calculations are shown in Figure 7.
Of
course, the results depend on the choices of the concrete plasma
parameters (which are given in the figure caption). In Figure 7,
the curves are related to the right-hand polarized ion-cyclotron
waves with frequencies above the proton gyrofrequency.
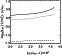
Figure 7
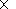 10-6 A m-2.
The curves shown in Figure 7
are related to highly oblique ion-cyclotron
waves.
The analysis showed that the
plasma instability is excited at lower values of the wave number
k if the FAC intensity becomes larger. On the order of magnitude,
the values of
g calculated by us correspond to those obtained
for the drifting plasma
of the near-Earth tail
by
Chaston et al. [1999].
On the other hand,
Xue et al. [1996]
obtained that the maximum
wave growth due to hot proton temperature anisotropy near the
geomagnetic equator at
L=7 is less
by one to two orders of magnitude than that described here.
10-6 A m-2.
The curves shown in Figure 7
are related to highly oblique ion-cyclotron
waves.
The analysis showed that the
plasma instability is excited at lower values of the wave number
k if the FAC intensity becomes larger. On the order of magnitude,
the values of
g calculated by us correspond to those obtained
for the drifting plasma
of the near-Earth tail
by
Chaston et al. [1999].
On the other hand,
Xue et al. [1996]
obtained that the maximum
wave growth due to hot proton temperature anisotropy near the
geomagnetic equator at
L=7 is less
by one to two orders of magnitude than that described here.
 1000 km). Instead, the region
of
plasma instability stretches to
higher altitudes in the auroral magnetosphere.
Besides, we can conclude that the
plasma instability is excited at lower values of the wave number
k if the
altitude becomes larger.
1000 km). Instead, the region
of
plasma instability stretches to
higher altitudes in the auroral magnetosphere.
Besides, we can conclude that the
plasma instability is excited at lower values of the wave number
k if the
altitude becomes larger.
4. Conclusions
Acknowledgments
V.E.Z. thanks the Gottlieb
Daimler and Karl
Benz Foundation for financing his stay at the Potsdam Astrophysical
Institute to work on the given topic.
C.-V.M. gratefully acknowledges financial support
from project 24-04/055-2000 of the Ministerium für
Wissenschaft, Forschung und Kultur des Landes Brandenburg, and from
project ME 1207/7 of the Deutsche Forschungsgemeinschaft.
References
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on December 7, 2002.