Accretion of magnetized plasma on a gravitational center

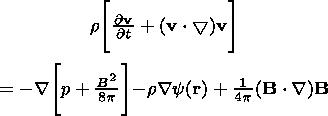
S. A. Dyadechkin and V. S. Semenov

Physical Institute, St. Petersburg University, St. Petersburg, Russia

H. K. Biernat

Space Research Institute, Austrian Academy of Sciences, Graz, Austria

Received 18 April 2001, published online 6 October 2001

Contents

Abstract

Introduction

It is well known these days that a star originates as a result of the collapse of interstellar clouds of magnetized molecular gas. Thus the process of star formation depends on the properties of a protostellar cloud, and to understand this process, we need to consider the accretion of magnetized plasma on a gravitational center. At some stage, the magnetic field becomes strong enough to modify profoundly the dynamics of gravitational contraction, in particular, by introducing an essential anisotropy into the problem [Mestel, 1985]. This makes, generally speaking, the problem a time-dependent and three-dimensional (3-D) one.

A similar situation occurs in many problems of space physics where the magnetic field strongly influences the plasma motion, for example, in the case of solar-wind-magnetosphere interactions [Biernat, 1991; Biernat et al., 1987]. In this case a relatively weak interplanetary magnetic field is amplified more than 10 times in the course of solar wind flow around the magnetosphere, producing a so-called magnetic barrier or depletion layer [Erkaev, 1989; Zwan and Wolf, 1976]. It turns out that such a problem with a strong magnetic field can be successfully solved using the thin flux tube approximation. The general idea of this approach is quite simple. We have to take a test flux tube and let it go with the solar wind in the case of the magnetosphere, or under the influence of gravitation in the case of star formation. The time evolution of this test flux tube can provide a clear physical description of a complicated 3-D time-dependent plasma flow.

For example, for the Earth's magnetosphere such an approach gives the famous Dungey model [Dungey, 1961], which can describe many important features of the solar wind-magnetosphere coupling: (1) the magnetic barrier (depletion layer) formation, (2) dayside magnetopause reconnection, (3) flux transfer from the dayside magnetosphere to the nightside, (4) the growth phase of a magnetospheric substorm (magnetic energy accumulation in the magnetotail), (5) reconnection in the magnetotail (magnetospheric substorm).

Of course, we cannot apply directly the Dungey model to the completely different process of plasma accretion on a gravitational center. Instead, we can make the following general conclusions, which we have to take into account for other applications:

1. In a first approximation the solar wind-magnetosphere coupling can be described in terms of flux tubes.

2. The inhomogeneous motion of space plasmas leads to the accumulation of Maxwellian tensions (magnetic energy).

3. The relaxation of accumulated Maxwellian tensions is achieved through magnetic reconnection.

4. Magnetic reconnection is initiated inside a small diffusion region as a result of the development of anomalous resistivity.

Thus our idea is as follows: We will consider the motion of a test flux tube in the vicinity of a gravitational center similar to the classical investigation of the motion of a test particle.

MHD Equations

From a mathematical point of view, to obtain the time evolution of a flux tube, we first need to formulate the appropriate equations. To this end we will introduce Lagrangian coordinates into the MHD equations to obtain a convenient mathematical formulation for the flux tube motion [Semenov and Erkaev, 1989].

The following system of MHD equations (in Gaussian units) describes the plasma behavior in the vicinity of a gravitational center:

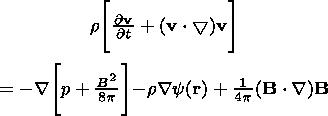(1)

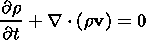(2)

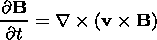(3)

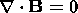(4)

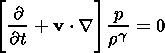(5)

Equation (1) is the equation of motion, (2) is the continuity equation, (3) is the induction equation (in the limit of infinite conductivity, i.e., Re_m 1, where Re_m is the magnetic Reynolds number), (4) encapsulates the solenoidity property of the magnetic field, and (5) is the equation of state. Here r, v, p, B, y, r, and g are the density, the velocity, the plasma pressure, the magnetic field, the gravitational potential, the space coordinate, and the ratio of specific heats, respectively.

Using dimensionless variables,

the system of equations (1)-(5) can be rewritten as (we shall omit the "*" from now on)

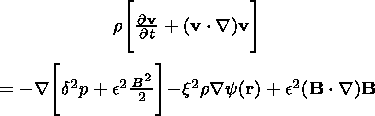(6)

(7)

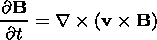(8)

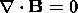(9)

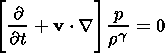(10)

Parameter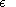s , x, and c are defined as

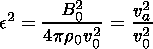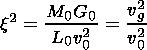(11)

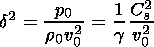where v_a and C_s are Alfvén and sound speed, respectively.

Frozen-in Coordinate System

Figure 1

The equation of motion (6) describes the behavior of a magnetic flux tube in the gravitational field. To appreciate this more fully, we have to rewrite (6), using a Lagrangian coordinate system (i.e., a coordinate system comoving with the magnetic flux tube).

The following conservation laws are satisfied in the process of the magnetic flux tube motion (Figure 1):

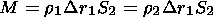(12)

the mass conservation law,

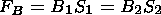(13)

and the flux conservation law. Therefore using (14) and (15), we can introduce a new variable a

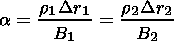(14)

Thus a is the mass of the magnetic flux tube with unit flux, and consequently, we can measure the length of a tube in units of mass. Another variable that we use is the Lagrangian time t (i.e., motion particle time along the trajectory). In this case, it can be shown that [Semenov and Erkaev, 1989]

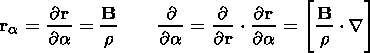(15)

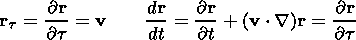(16)

consequently,

(17)

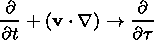(18)

Furthermore, we can use (15)-(18) and rewrite the equation of motion (6) in frozen-in coordinates. Thus we derive the following system of equations:

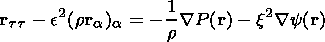(19)

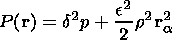(20)

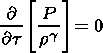(21)

The MHD equation of motion (6), written in frozen-in coordinates is the equation of a nonlinear string, which is well known in mathematical physics and plays an important role in the description of many wave-like processes. The left-hand side of (19) has the form of the 1-D nonlinear string equation and the right-hand side incorporates the effects of the total pressure and gravitational potential. Therefore we can establish an analogy between the nonlinear string and the magnetic flux tube. This description is very convenient for various problems, because often it gives important physical insight [Erkaev, 1989]. In our case, it is more convenient to consider an isolated magnetic flux tube.

There is another way to bring out the analogy between the magnetic flux tube and the nonlinear string. This can done by employing the variational method.

We can write the Lagrangian L for the magnetic flux tube as

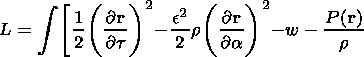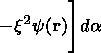(22)

where w is the internal energy of the plasma, w=d²k[r^g-1/ (g-1)]. The Hamiltonian H is written as

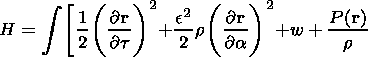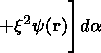(23)

Furthermore, we can use the variational method and derive the system of MHD equations in frozen-in coordinates (19)-(20).

Also, we can extract a useful property from the Hamiltonian (23). Integrating with respect to time, we have

(24)

where W_k and W_p are the kinetic and potential energy respectively,

(25)

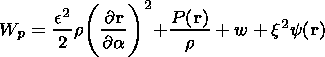(26)

From (24) we can see that the variation of the total energy in the magnetic flux tube is equal to the flux through the ends.

To investigate the behavior of a magnetic flux tube falling toward a gravitational center, we solve the system of equations (19)-(21) using a Lax-Wendroff numerical method. This is a two-step method that is often used for the solution of similar problems.

Results of the Numerical Simulation

The motion of a free particle is well known [Landau and Lifschits, 1988]. In a gravitational center, a free particle moves along Kepler orbits, and if a particle has a nonzero impact parameter, it never can be captured by a gravitational center. For the particles in the magnetic flux tube, the motion is evidently different from that of a free particle, because the magnetic field will put a brake on the tube element (particle). Thus as it loses angular momentum and energy, a particle will change its orbit gradually, approach the gravitational center, and finally it will be captured.

Figure 2

As initial conditions for the numerical simulation we take an undisturbed magnetic flux tube with length l, a distance to the gravitational center of L, and an impact parameter P (Figure 2). Quantities L, l, and P are supposed to satisfy the following conditions:

(27)

Furthermore, we perform a parametric investigation of the string behavior, varying parameters 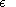, x, and c and considering their influence on the string motion.

We obtain the following results: There are two different kinds of motion of the magnetic flux tube in the vicinity of the gravitational center: capture of the string, and free string motion.

In the case of the string capture (Figure 2), the central part of the flux tube begins to fall toward the gravitational center faster than distant parts. The closer points of the string are located at the gravitational center, the faster they move. Thus the distance between the central part and the other parts of the flux tube increases and the flux tube is strongly stretched toward the gravitational center. The numerical simulation in this case is continued up to the moment when the central point of the string reaches a small region around the gravitational center.

Figure 3

In Figure 3 we see the density behavior in this case. During the string motion, the density increases in the central part of the flux tube. The plasma from distant regions of the flux tube flows toward the central part of the string under the influence of the gravitational center. The more mass flows into the central region of the flux tube, the stronger the influence of the gravitational center on the unit element of the central part of the string. Thus the central part of the string falls onto the gravitational center faster and faster until it is finally captured. Evidently, the magnetic field in the string is increased as a consequence of the stretching of the flux tube.

Figure 4

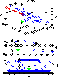
The second case is the free string motion (Figure 4).

In the case of a free string motion, the influence of the gravitational field on the flux tube is less pronounced than in the previous case. In this case the gravitational field does not capture the string but changes the direction of the flux tube motion (Figure 4). At first the string is strongly stretched under the influence of the gravitational center, as in the case of string capture. However, after passing through the immediate neighborhood of the gravitational center, the shape of the string recovers the initial undisturbed configuration.

Figure 5

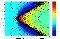
In the case of the free string motion, the density behavior is similar to the case of string capture at first. However, after passing the closest point to the gravitational center, the character of the motion changes. Under the influence of the gravitational field, two oppositely directed MHD waves are generated in the string (Figure 5). They move along the flux tube from the central part to the distant regions of the string and modify the density in the flux tube. The string density increases after passage of the waves. As a result, the density along the string increases and the string, as a whole, is compressed (Figure 4). It is clear why such an effect takes place, because the mass conservation law has to be satisfied in the magnetic flux tube.

Thus in this case, the gravitational center influences the string similar to the influence of a displacement along an infinite string. It is well known that after the displacement, an infinite string just changes its position without a change of shape. In the case of the free string motion we have a similar effect. However, in our case, the gravitational center changes the direction of the string motion and density in the flux tube.

Figure 6

It is well known that if the free particle has a nonzero impact parameter, it can never be captured by the gravitational center. However, the string can be captured. Thus there is a strong difference between the free particle motion and the motion of string particles. This difference is the result of the magnetic field influence on the particles in the flux tube. In Figure 6 we can see that even a weak magnetic field has a strong influence on the motion of flux tube particles.

Figure 7

The reconnection process can radically change the kind of motion of the magnetic flux tube in the gravitational field. During the string motion, there is the possibility of the appearance of a flux tube configuration like as Figure 7. Different parts of the magnetic flux tube with oppositely directed magnetic field are located close to each other. We note that the approach of a single flux tube is rendered invalid at this moment. A detailed consideration of conditions for the initiation of reconnection is out of the frame of this study.

We assumed that the reconnection process occurs at this moment. As a result, the string is divided into two parts. The first part rapidly falls toward the gravitational center, and the second part moves away.

Conclusions

1. The behavior of a magnetic flux tube is radically different from free particle motion. The string with the nonzero impact parameter can be captured by a gravitational center. However, the free particle with a similar parameter will never be captured. Thus there are two types of string behavior in the vicinity of the gravitational center: capture of the string, and the free motion of the string.

2. In the case of the free string motion, two oppositely directed waves are formed in the flux tube, which propagate from the central part of the string to distant regions of the flux tube and increase the string density.

3. The reconnection process has a major influence on the string behavior and can change the kind of string motion.

Acknowledgments

References

Biernat, H. K., Coupling processes at the magnetopause, in Theoretical Problems in Space and Fusion Plasma, pp. 105-118, Austrian Academy of Sci. Press, Graz, Austria, 1991.

Biernat, H. K., M. F. Heyn, and V. S. Semenov, Unsteady Petschek reconnection, J. Geophys. Res., 92, 3392, 1987.

Dungey, J. W., Interplanetary magnetic field and the auroral zones, Phys. Rev. Lett., 6, 47, 1961.

Erkaev, N. V., A solar wind flowing over the Earth's magnetosphere, in Solar Wind-Magnetosphere Interaction, Results of Researches on the International Geophysical Projects, Moscow, Russia, 1989.

Landau, L. D., and E. M. Lifschits, Mechanics, Nauka, Moscow, Russia, 1988.

Mestel, L., Magnetic Field, Protostars and Planets II, pp. 320-339, Kluwer Academic Publishers, 1985.

Semenov, V. S., and N. V. Erkaev, Non-linear strings, Geomagn. Aeron. (in Russian), 29, 222, 1989.

Zwan, B. J., and R. A. Wolf, Depletion of solar wind plasma near the planetary boundary, J. Geophys. Res., 81, 1636, 1976.