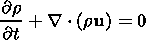
C.-V. Meister
Astrophysical Institute Potsdam, Potsdam, Germany
Received 5 April 2001, published online 22 January 2002
Studying global solar oscillations, properties in the velocity and radiation intensity fluctuations of the acoustic-type modes (called p modes) were found, which provides a reason to conclude that the waves behave nonadiabatically [e.g., Deubner, 1991]. The most probable reasons for this nonadiabaticity are interactions between the acoustic waves and the processes of radiation and heat transport as well as turbulence. First theoretical investigations of the visibility of the luminosity variations of the Sun correlated with p modes were performed by Toutain and Gouttebroze [1988, 1993].
The interpretation of the wave observations was mostly limited by adiabatic models. In general, the nonadiabatic models are yet restricted to the case of gray, homogeneous atmospheres. Thus the further development of the theory of nongray and nonhomogeneous atmospheres stratified in the gravity field and structured by the magnetic field is needed to understand the more and more detailed experimental data.
Thus Ibánez and Plachco [1989] introduced in the basic radiation magnetohydrodynamic equations of ideal gases [Mihalas and Mihalas, 1984] the electron heat conductivity. Already Souffrin [1972] obtained a dispersion equation of nonadiabatic waves for an isothermal atmosphere using the Newton approximation for the radiation relaxation. Zhugzhda [1983] found an analytical solution for nonadiabatic waves in an isothermal atmosphere with density-dependent radiation transport. Further, in 1991, he presented a general solution for the fundamental mode of any atmosphere at all.
However, in all the publications mentioned, the magnetic field was neglected. The influence of the magnetic field in an isothermal stratified atmosphere was first considered by Babaev et al. [1995], who used the Newton approximation for the radiation loss term.
Staude et al. [1994] studied nonadiabatic hydrodynamic waves, for example, the 5-min oscillations of the solar photosphere and chromosphere, in a homogeneous, nongray, radiating and thermally conducting atmosphere under the condition of thermal equilibrium. It was found that the heat conductivity by particle collisions only (neglecting effective wave-particle collisions) seems to be less important than the heat conductivity due to the radiation transport.
In general, the numerical modeling of the nonadiabatic waves in radiating atmospheres showed that also the further development of analytical solutions is of importance, on the one side, to define the boundary conditions for the numerical calculations [Dzhalilov et al., 1992] and, on the other side, to guarantee a better analysis of the numerical results. Thus an analytical study of the radiation hydrodynamics of a stratified atmosphere is presented here.
To describe low-frequency phenomena in a fluid plasma system with radiation transport being influenced by a gravity force, one can use radiation hydrodynamics. This means that the continuity equation
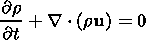 | (1) |
the momentum balance
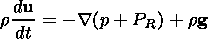 | (2) |
and the energy balance of a nonadiabatic plasma system
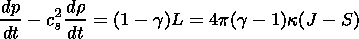 | (3) |
should be considered:
d/dt=(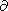 /
/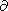 t+ u
t+ u
 ),
where
r is the mass density,
p is the scalar pressure,
r u is the
momentum density,
g is the gravitational acceleration,
and
g is the adiabatic coefficient of the plasma.
S is the radiation source function,
J represents the mean intensity of the
scattered radiation field,
L describes the radiation loss function,
and
k designates the opacity.
Taking into account that the square of the sound velocity
is equal to
c2s=gp/r,
one can also present (5) in the form
),
where
r is the mass density,
p is the scalar pressure,
r u is the
momentum density,
g is the gravitational acceleration,
and
g is the adiabatic coefficient of the plasma.
S is the radiation source function,
J represents the mean intensity of the
scattered radiation field,
L describes the radiation loss function,
and
k designates the opacity.
Taking into account that the square of the sound velocity
is equal to
c2s=gp/r,
one can also present (5) in the form
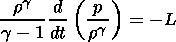 | (4) |
Further, it is assumed that the thermodynamic equation of an ideal gas is applicable:
 | (5) |
where m is the mean molecular weight. The radiation pressure PR is given by Mihalas and Mihalas [1984]
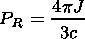 | (6) |
The source function S of the electromagnetic radiation is assumed to be equal to the Planck function
 | (7) |
where
s = (2 p5
kB4) / (15 h3 c2)
= (5.6697  0.0029)
0.0029)  10-8 W m
2 K
-4 is the Stefan-Boltzmann constant.
10-8 W m
2 K
-4 is the Stefan-Boltzmann constant.
The momentum and energy equations for the radiation field are used in the Eddington approximation [Mihalas and Mihalas, 1984]
 | (8) |
 | (9) |
J is defined as a specific intensity averaged over all solid angles:
 | (10) |
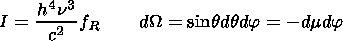 | (11) |
where fR is the photon distribution function; that is fR( r, t, n, p) d p is the number of photons, per volume, at place r and time t, with the momentum lying in the interval ( p, p+d p)=(hn/c)( n, n+d n). The n value points into the direction of the propagation of the radiation. H is the Eddington flux, which is defined by the first angular momentum of the specific intensity
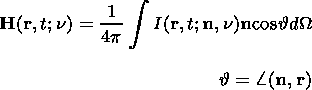 | (12) |
This means that (8) and (9) describe isotropic media such as the spherical and the one-dimensional planar ones; n designates the photon frequency, h is the Planck constant, and c is the speed of the light. For the sake of simplicity, we do not distinguish between the flux-mean opacity (in (8)) and the intensity-mean opacities (equations (3) and (9)). Such an approximation was also introduced by Bogdan and Knölker [1989] for the magnetized nonstratified solar atmosphere. The system of equations (1)-(3), (8), and (9) forms a full system of equations for the three scalar parameters r, p, T, and the vector u.
It is assumed that the plasma is gray and that it is slightly disturbed from its altitude-dependent equilibrium state (designated by the index "o")
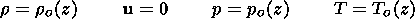 | (13) |
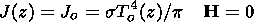 | (14) |
The equilibrium value of the radiation intensity Jo is found equating I in (12) with the Kirchhoff-Planck function
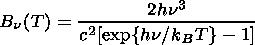 | (15) |
and then averaging the result over the frequency n. The equilibrium values of the source function So and the radiation intensity Jo coincide.
The plasma and field parameters may be expressed by the sum of the equilibrium values and the disturbances, which are designated by the index "1,"
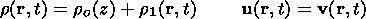 | (16) |
 | (17) |
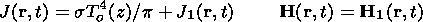 | (18) |
Further, an attempt is made to derive the dispersion equation of nonadiabatic waves in the nonhomogeneous solar substance and to find a way to obtain relations between the wave amplitudes of different plasma parameters. For the interpretation of experimental data on the solar atmosphere, it is especially important to study temperature and radiation intensity fluctuations. The method used here is analogous to the method applied for the case when the loss term L=0 by Roberts [1991].
Taking into account the radiation pressure (6), the equilibrium momentum balance (2) is written as ( g=-g nz )
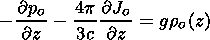 | (19) |
Further, expressing the mean radiation intensity Jo by (14) and To(z) by the effective solar temperature
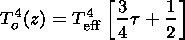 | (20) |
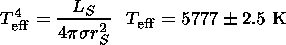 | (21) |
T eff is the effective temperature of a blackbody of solar radius
rS=(6.9626 0.0007)
0.0007) 108 m,
which radiates with the total solar luminosity
LS=(3.845
108 m,
which radiates with the total solar luminosity
LS=(3.845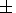 0.006)
0.006)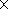 1026 W.
Value
t is the optical depth of the
solar atmosphere, which is assumed to be gray, which that means
1026 W.
Value
t is the optical depth of the
solar atmosphere, which is assumed to be gray, which that means
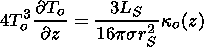 | (22) |
and
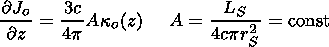 | (23) |
Finally, one obtains the equilibrium condition
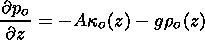 | (24) |
where
A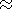 0.2105 N m
-2 is known.
For
g the gravitational acceleration at the
solar surface
g=274 m s
-2 will be used.
0.2105 N m
-2 is known.
For
g the gravitational acceleration at the
solar surface
g=274 m s
-2 will be used.
On the other side, To in the equilibrium formula Jo=sT4o/p, can be expressed by the equation of state,
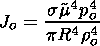 | (25) |
Forming the
z derivative of
Jo given by (25),
and equating the result with
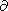 Jo/
Jo/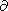 z of (24),
one has
z of (24),
one has
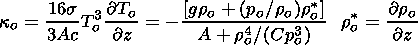 | (26) |
 | (27) |
This relation gives a possibility to estimate ko using tables of ro and po found within the standard solar model. A comparison of the results with available opacity values allows an evaluation of the quality of the theory developed here of nonadiabatic solar waves. It should be also mentioned that deriving (26) and (27), the mean molecular weight m was taken to be altitude-independent. An improvement of (26) and (27) for altitude-dependent m(z) can easily be done.
In the case of low-temperature solar plasma with log
T
< 3.85,
opacity tables with an accuracy of about
10-3 are available
(see, for example, the review by
Gong and Däppen [1998]).
In the solar atmosphere about 300 km thick ( t 1 ),
the opacity averaged over the frequency is about
3
1 ),
the opacity averaged over the frequency is about
3 10-8 cm
-1.
For the Sun in general, typical values
of the opacity per unit of mass are
0.5
10-8 cm
-1.
For the Sun in general, typical values
of the opacity per unit of mass are
0.5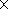 104 cm
2 g
-1 [Weigert and Wendker, 1996].
104 cm
2 g
-1 [Weigert and Wendker, 1996].
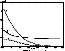
|
| Figure 1 |
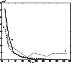
|
| Figure 2 |
 11,000 K.
It is clear that within the very simple model presented here
with constant
m,
only the order of magnitude of the opacity in certain solar regions
may be reproduced.
11,000 K.
It is clear that within the very simple model presented here
with constant
m,
only the order of magnitude of the opacity in certain solar regions
may be reproduced.
Considering the radiation equilibrium described by (8) and (9), one finds the relations
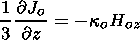 | (28) |
and
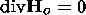 | (29) |
Equation (28) shows that in the case of nonuniform temperature the
mean Eddington flux does not vanish. Considering only vertical gradients
in the plasma, relation (29) results into a constant
z component of the mean Eddington flux.
Expressing
 Jo/
Jo/ z by (23), one obtains
z by (23), one obtains
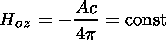 | (30) |
For the linearized momentum balance, one finds from (2)
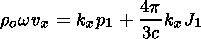 | (31) |
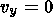 | (32) |
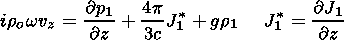 | (33) |
The linearized continuity equation has the form
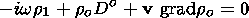 | (34) |
Here
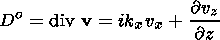 | (35) |
The corresponding energy balance for the disturbances is
(using
dr/dt=-r v )
v )
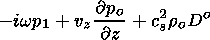 |
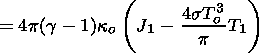 | (36) |
Expressing
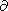 po/
po/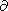 z in (36) by (3), and
T1 by
the linearized equation of state
z in (36) by (3), and
T1 by
the linearized equation of state
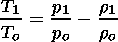 | (37) |
one obtains
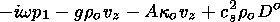 |
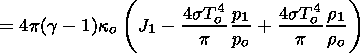 | (38) |
The equations (31)-(34) and (38) describe the disturbances of the plasma parameters r1, v, and p1, which are coupled to the radiation field by J1. The latter value has to be found from (8) and (9).
For the disturbances of the radiation field, one finds from (8), (9), and (30)
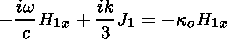 | (39) |
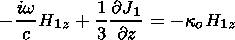 | (40) |
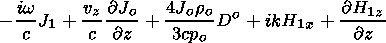 |
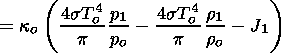 | (41) |
Expressing
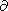 Jo/
Jo/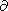 z in (41) by (23) and (28),
and substituting
H1x by (39) and
H1z by (40),
one obtains for the dependence of the radiation intensity
J1 on the plasma disturbances the following formula:
z in (41) by (23) and (28),
and substituting
H1x by (39) and
H1z by (40),
one obtains for the dependence of the radiation intensity
J1 on the plasma disturbances the following formula:
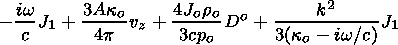 |
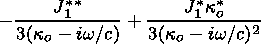 |
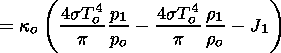 | (42) |
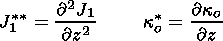 |
Now (31), (33)-(35), (38), and (42) have to be used to derive the dispersion equation of the nonadiabatic waves. These equations describe the disturbances vx, vz, p1, J1, r1, and Do.
As a next step, r1 will be excluded from the system of equations. Therefore r1 from (34),
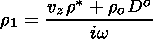 | (43) |
is substituted into (33), (38), (42). One finds then
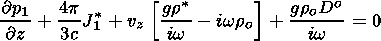 | (44) |
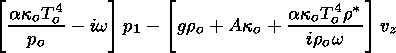 |
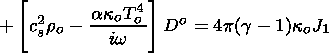 | (45) |
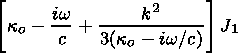 |
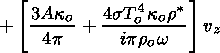 |
 |
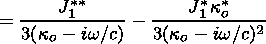 | (46) |
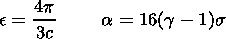 | (47) |
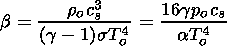 | (48) |
Further, expressing vx by (31), Do one can transform (35) into
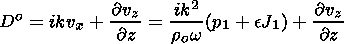 | (49) |
and (44)-(46) and (49) describe p1, J1, vz and Do. Further, we try to exclude p1 and vz from the systems of equations, and to find an equation for Do (according to the method of solution for the plasma without radiation) containing an additional J1 contribution.
Thus first we exclude Do from (44) to (46) and find p1 and vz as a function of J1. Thus Do from (49) will be substituted into (44)-(46) to obtain
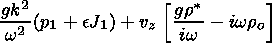 |
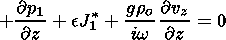 | (50) |
 |
 |
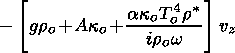 |
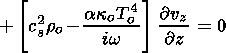 | (51) |
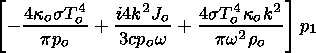 |
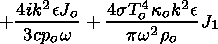 |
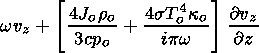 |
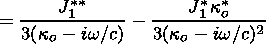 | (52) |
Considering
the limit of infinite Boltzmann number
b (which is mathematically equivalent to
s 0,
e.g.,
Jo
0,
e.g.,
Jo 0 ) in the
energy balances (51) and (52), one can simplify the
latter relations
0 ) in the
energy balances (51) and (52), one can simplify the
latter relations
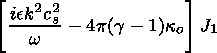 |
 | (53) |
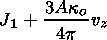 |
 | (54) |
Substituting
p1 from (45) (in the limit
s 0 )
0 )
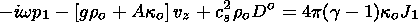 | (55) |
into (49) for Do, one finds
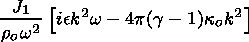 |
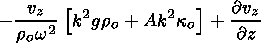 | (56) |
Then, forming the
z derivative of (55) and substituting into the
result the expression for
 vz/
vz/ z found from (56),
one has
z found from (56),
one has
 |
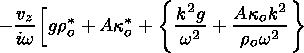 |
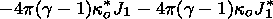 |
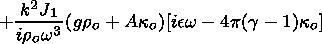 | (57) |
Now
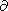 p1/
p1/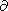 z from (57) is substituted into (44).
Using the relation
z from (57) is substituted into (44).
Using the relation
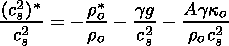 | (58) |
one finds
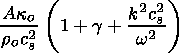 |
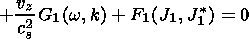 | (59) |
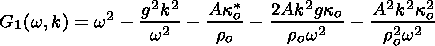 | (60) |
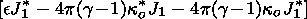 |
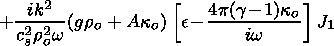 | (61) |
The z derivative of (59) is written as
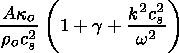 |
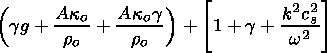 |
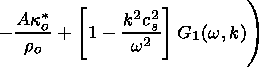 |
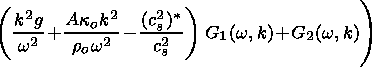 |
 | (62) |
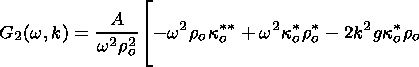 |
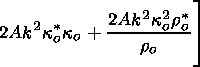 |
 |
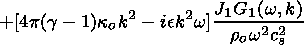 | (63) |
Multiplying (59) by
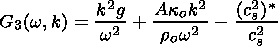 | (64) |
and subtracting (62) from the result, one obtains
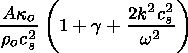 |
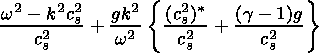 |
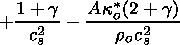 |
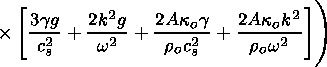 |
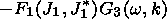 |
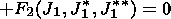 | (65) |
In the case of a vanishing radiation transport J=0, A=0, (65) may be transformed into a simple relation:
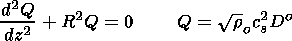 | (66) |
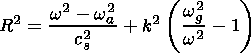 | (67) |
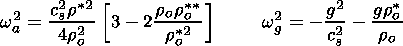 | (68) |
where wa and wg are the acoustic cutoff frequency and the buoyancy frequency of a stratified atmosphere without radiation transport. For linear temperature profiles, a solution of (66) was first found by Lamb [e.g., Roberts, 1991]. This solution may be represented by confluent hypergeometric functions. In all other cases (66) and above all (65) for systems with radiation transport have to be solved numerically.
1. Therefore first the fluctuations of the
intensity of the scattered radiation field have to be found.
Thus
Do from (56) (with
vz from (54) and
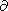 vz/
vz/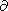 z from the
z derivative of (54)) and
Do* from the
z derivative
of (56)
(with
vz,
z from the
z derivative of (54)) and
Do* from the
z derivative
of (56)
(with
vz,
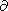 vz/
vz/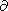 z,
z,
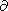 2 vz/
2 vz/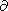 z2 from (54) and its
z derivatives)
have to be substituted into (59). Consequently, a
differential equation of the
fourth order for
J1 with respect to
z will be found, which has to be
solved for given boundary conditions.
z2 from (54) and its
z derivatives)
have to be substituted into (59). Consequently, a
differential equation of the
fourth order for
J1 with respect to
z will be found, which has to be
solved for given boundary conditions.
2. If one has obtained J1, the solution for vz may be obtained from (54).
3. Knowing J1 and vz, one may further determine p1 using, for example, (53).
4. After that, it is possible to find vx using (31).
5. Then, with the help of (42) (expressing Do by (56)), r1 may also be found.
6. From (37), one determines then temperature fluctuations especially important for interpretation of satellite experiments T1.
7. Besides, from (39) and (40), one may obtain H1x and H1z, respectively.
Applications of this method to find the fluctuations of the parameters of the solar plasma and the radiation field will be presented in further papers.
In the present paper, former models of hydrodynamic adiabatic atmospheric waves are extended to the case of nonadiabatic acoustic-gravity waves in a system with radiation transport where the radiation relaxation is described in the Eddington approximation.
Effects of the stratification of the atmosphere are taken into account, but no influence of the mean magnetic field is considered. The temperature distribution is assumed to be nonuniform, and an altitudinal-dependent radiation pressure is taken into account in the momentum balances.
In analogy to the works for stratified plasmas neglecting nonadiabatic effects, a dispersion relation is found introducing the divergency of the plasma velocity as a new parameter. In the obtained dispersion relation, there appear new radiation-intensity-dependent coefficients and additional terms describing the wave damping by the radiation transport.
The momentum and energy balances for the particles and the radiation are studied here, contrary to other works. Thus a simple approximate relation between the opacity and the mean plasma pressure, the mean pressure gradient and the mass density is found. This relation may be used to estimate the quality of the model developed for the atmospheric acoustic-gravity waves. Since, for the sake of simplicity, the mean-molecular-weight gradients in the system are neglected here, one is able to estimate only the order of magnitude of the opacity.
A scheme is given, which indicates how to find successively the amplitudes of the plasma (velocity, mass density, pressure, temperature) and radiation field (radiation intensity, Eddington flux) parameters in a stratified atmosphere where hydrodynamic acoustic-gravity waves exist. To apply this scheme, boundary conditions for the radiation intensity fluctuations and their spatial derivaties up to the fourth order have to be taken into account.
Analytical expressions to calculate the amplitudes of the plasma and radiation field variations are presented for the case of a large Boltzmann number of the substance, i.e. for relatively cold atmospheres with high plasma pressure and rather low mass density, or for a substance with a polytropic coefficient of the order of unity. The obtained results may be used for the interpretation of experimental data obtained during the solar satellite experiments, e.g., CORONAS and SOHO.
Babaev, E. S., N. S. Dzhalilov, and Y. D. Zhugzhda, Nonadiabatic magneto-acoustic-gravity waves in a stratified atmosphere, Astron. Rep., 39, 211, 1995.
Bogdan, T. J., and M. Knölker, On the propagation of compressive waves in a radiating magnetized fluid, Astrophys. J., 339, 579, 1989.
Deubner, F.-L., Observations of waves and oscillations, in Mechanisms of Chromospheric and Coronal Heating, Springer-Verlag, New York, 1991.
Dzhalilov, N. S., Y. D. Zhugzhda, and S. Staude, Radiation-hydrodynamic waves in an optically grey atmosphere, I, Homogeneous model, Astron. Astrophys., 257, 359, 1992.
Gong, Z., and W. Däppen, The influence of low-temperature opacity on solar models and p mode frequencies, in Proceedings of the SOHO 6/GONG 98 Workshop on "Structure and Dynamics of the Interior of the Sun and Sun-like Stars," ESA SP-418, 465 pp., Eur. Space Agency, Paris, France, 1998.
Ibánez, S. M. H., and M. F. P. Plachco, Effects of the thermal conduction on the propagation of linear waves in a radiating fluid, Astrophys. J., 336, 875, 1989.
Kurucz, R. L., Model atmospheres for G, F, A, B, and O stars, Astrophys. J. Suppl. Series, 40, 1, 1979.
Mihalas, D., and B. W. Mihalas, Foundations of Radiation Hydrodynamics, Oxford Univ. Press, New York, 1984.
Roberts, B., Magnetohydrodynamic waves in the Sun, in Advances in Solar System Magnetohydrodynamics, edited by E. R. Priest, and A. W. Hood, chap. 6, 105 pp., Cambridge Univ. Press, New York, 1991.
Souffrin, P., Radiative relaxation of sound waves in an optically thin isothermal atmosphere, Astron. Astrophys., 17, 458, 1972.
Staude, J., N. S. Dzhalilov, and Y. D. Zhugzhda, Radiation hydrodynamic waves and global solar oscillations, Solar Phys., 152, 227, 1994.
Toutain, T., and P. Gouttebroze, Visibility of nonradial pulsations in solar continuum intensity measurements, in Seismology of the Sun and Sun-like Stars, edited by E. J. Rolfe, ESA-SP 286, 241 pp., Eur. Space Agency, 1988.
Toutain, T., and P. Gouttebroze, Visibility of solar p modes, Astron. Astrophys., 268, 309, 1993.
Weigert, A., and H. J. Wendker, Astronomie und Astrophysik. Ein Grundkurs, VCH Verlagsgesellschaft, Weinheim, 1996.
Zhugzhda, Y. D., Non-adiabatic oscillations in an isothermal atmosphere, Astrophys. Space Sci., 95, 255, 1983.
Zhugzhda, Y. D., On the problem of f mode generation in the solar atmosphere, Solar Phys., 132 (2), 205, 1991.