Instability of the magnetopause with a finite curvature radius and velocity shear

I. L. Arshukova and N. V. Erkaev

Institute of Computational Modeling, Russian Academy of Sciences, Krasnoyarsk, Russia

H. K. Biernat

Space Research Institute, Austrian Academy of Sciences, Graz, Austria

Received 14 August 2001, published online 16 January 2002

Contents

Abstract

Introduction

The interchange instability is similar in nature to the Rayleigh-Taylor instability in classical hydrodynamics, where the magnetic stress plays the role of an effective gravitational force [Chandrasekhar, 1968; Freidberg, 1987].

Concerning the high shear subsolar magnetopause, the possibility of the interchange instability was discussed by Alexeev and Maltsev [1990] and Rezenov and Maltsev [1994]. In the particular case of a southward interplanetary magnetic field (IMF), the plasma pressure has a maximum at the point where the magnetic field strength is zero inside the magnetopause under constancy of the total pressure across the magnetopause. Assuming a local enhancement of the plasma pressure at a tangential discontinuity, they estimated the instability growth rate for the magnetopause as a function of the local curvature radius.

As was shown by Arshukova and Erkaev [[2000], the thickness of the magnetopause is an important parameter that affects substantially the interchange instability growth rate. Additional aspects to be studied are those related to a velocity shear at the magnetopause which drives the Kelvin-Helmholtz instability and has a strong influence on the interchange instability.

As was shown by Luhman et al. [1984], areas of nearly antiparallel magnetic field have locations that depend on the IMF orientation. Generally, velocity shear has to be taken into account for high magnetic shear regions located far away from the subsolar point. In the particular case of northward IMF, antiparallel magnetic field components occur in the nightside of the magnetosphere, where the velocity of plasma flowing around the magnetosphere is rather large and directed along the magnetic field. In the case of a southward IMF, there is a large area of nearly antiparallel magnetic fields on the dayside magnetopause which has a long spatial extension in both the meridional and the equatorial planes. The plasma velocity is directed parallel to the magnetic field in the meridional plane and perpendicular to the magnetic field in the equatorial plane.

The aim of our paper is to study the interchange instability of the magnetopause taking into account plasma velocity which has an arbitrary direction along the magnetopause and allowing for finite thickness and nonzero curvature.

Statement of Problem

Figure 1

We consider the magnetopause to be a thin layer (see Figure 1) of thickness 2 a. This layer has two boundaries: the first is that of contact with the magnetosheath ( F₁ ) and the second is that of contact with the magnetosphere ( F₂ ). The magnetic fields of the magnetosheath and the magnetosphere are denoted by vectors B₁ and B₂, respectively, and the magnetic field inside the layer, B₀, is determined as the vector average: B₀ = ( B₁ + B₂ )/2. The direction of plasma flow is determined by the angle a between the velocity vector and the geomagnetic field ( z axis).

To describe temporal and spatial variations of the magnetic field and plasma parameters resulting from small perturbations of the boundaries F₁ ( x₁ =f₁(y,z,t) ) and F₂ ( x₂ = f₂(y,z,t) ), we use the ideal magnetohydrodynamics (MHD) equations (in Gaussian units) in the incompressible case [Landau and Lifshitz, 1960]:

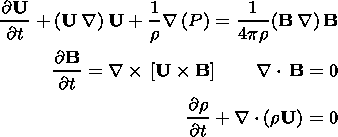(1) (2) (3)

Here r, U, P, and B are the density, velocity, total pressure, and magnetic field strength, respectively.

Assuming F₁ and F₂ to be tangential discontinuities, we have no-flow conditions for the normal components of velocity:

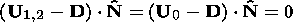(4)

where D is the speed of the boundary surface and N is the unit vector normal to the boundary surface. In addition, we have the balance of the total pressure at both boundaries:

(5)

Hereinafter, subscripts "1, 0, 2" denote magnetic field and plasma parameters in the following three regions, respectively: in the magnetosheath, inside the layer, and in the magnetosphere.

Generally, the surface of the magnetopause is characterized by two main local curvature radii, R_y and R_z. In a small neighborhood of the chosen point on the surface, we introduce a local coordinate system with respect to the surface. The two coordinates y and z are the distances along the curves on the surface with curvature radii R_y and R_z, respectively. The third coordinate x is the distance along the normal to the surface.

We introduce small perturbations of the magnetic field and plasma parameters as follows:

where b B, p P, u U.

Assuming, that B^*_x and U^*_x are equal to zero, we obtain from (1) the following equations in a linear approximation:

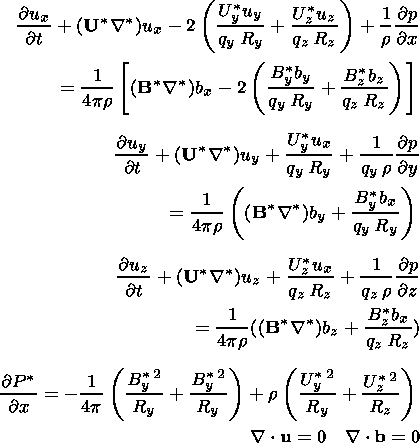(6)      (7)     (8)     (9)  (10)

Here ^* is a vector operator defined as

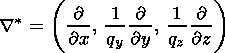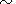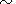where q_y and q_z are the metric coefficients related to the curvature q_y = 1 + x/R_y, q_z = 1 + x/R_z. It is important to note that we incorporate only the first-order terms with respect to the curvature 1/R_y, 1/R_z.

Initially, the plasma is assumed to satisfy the steady-state condition and thus the gradient of the total pressure is assumed to compensate magnetic stress and to support the normal centrifugal acceleration of plasma flowing around the curved surface. Therefore the initial total pressure is a function of the normal distance x which is linearized near the surface as follows:

(11)

where P₀ is a constant parameter. Variation of the total pressure determined by (11) is caused by magnetic field tension and centrifugal force.

From (2) and (3), we obtain in a linear approximation

(12)    (13)    (14)    (15)

For simplicity, we consider the two curvature radii to be equal to each other: R_y = R_z = R. For computational convenience, we introduce the dimensionless parameters K = k a,    r = R/a,    r_i = r_i/r₁,    H_i = B^*_i/B^*₂,    x = x/a,    h_i = b_i/B^*₂,    V_i = U_i^* 4pr₁/B^*₂,    v_i = u_i 4pr₁/B^*₂,    w = w4pr₁a/B₂^*, and p = p 4p/B₂^*2. We use a dimensionless small parameter e = 1/kR = 1/Kr which treated in a linear approximation. We also adopt the following inequality relation: a l R.

We can apply the usual Fourier method to solve our linear MHD problem. Thus considering all perturbations to be proportional to the complex exponential function exp(i( K s- w t)), where s is a two-dimensional vector in the plane ( yz ), we obtain from (6)-(10) the following:

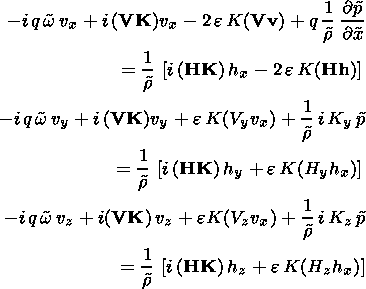(16)

where q = q_y = q_z = 1 + e K x. In the dimensionless form, equation (11) can be rewritten as

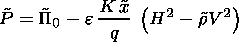(17)

After normalization, the system of equations (12)-(15) yields

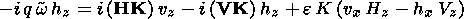(18)

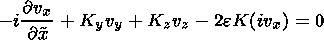(19)

Using continuity equation (19) together with equations (16) and (18), we obtain a differential equation for the total pressure:

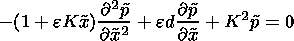(20)

where

Instability of One Boundary

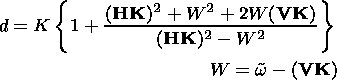At first, we start off with the simplified statement of problem, which is similar to that studied by Rezenov and Maltsev [1994]. This simplified statement concerns the interchange instability of one boundary F₁ separating the magnetosheath magnetic field from that inside the magnetopause.

In this case, the dimensionless differential equation for pressure (20) is simplified:

(21)

p₁ = c₁ exp(-k₁ x) and p₀ = c₀ exp(k₀ x), where k₁>0, k₀>0 are the solutions of equation (21).

From the boundary conditions (4) and (5) we obtain

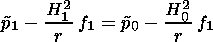(22)

From the equations (16), (18), and (22), we obtain a linear algebraic system for the coefficients c₁, c₀, f₁:

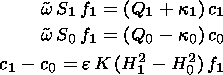(23)

where

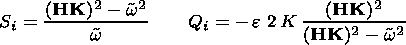(24)

We have the following algebraic equation for the growth rate of instability:

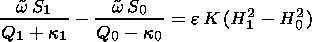(25)

Equation (25) determines the growth rate of interchange instability of one boundary as a function of the magnetosheath magnetic field direction (angle q ), wave number ( k ), and local curvature radius of the magnetosphere ( R ).

Problem With Two Boundaries

In this section, we study the interchange instability taking into account a finite thickness of the subsolar magnetopause and a nonzero velocity of the plasma flow.

We seek for a solution of equation (20) in an exponential form: p = C(x) exp(k⁰ x) = (C⁰ + eC¹(x)) exp(k⁰ x). Therefore we have exponential solutions for p in three regions. In the regions above F₁ and below F₂ (see Figure 1), perturbations of the total pressure are given by the following equations:

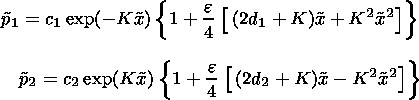(26)

In the region between F₁ and F₂, the solution for the total pressure is a combination of two exponential functions:

(27)

Here c₁, c₂, c₀₁, c₀₂ are constants.

In dimensionless form, the linearized conditions for total pressure and velocity are

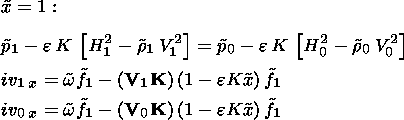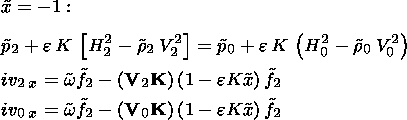(28)

Assuming that r₁ = r₂ = r₀ = 1, finally we obtain from equations (16) to (18) and (28) a linear algebraic system for parameters c₁, c₀₁, c₀₂, c₂, f₁, and f₂:

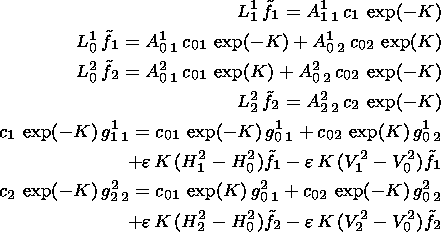(29)

where

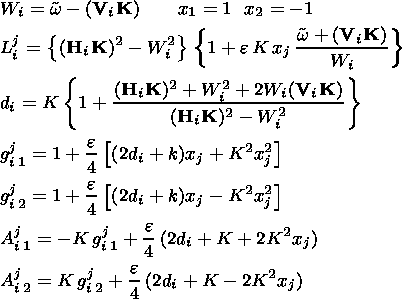(30)

Results

The dispersion equations are solved numerically for both instability problems (with one and two boundaries) For the first problem, the instability growth rate is obtained from (25) as a function of three parameters: k a, R/a, q. For the second problem, the dispersion equation is determined by (29), and the instability growth rate is obtained as function of four parameters: k, R/a, q, U/V_a2. In each plot, the instability growth rate is normalized to the quantity g^* = U_a2/a = B₂/4pr a.

Figure 2

Figure 2 shows the instability growth rate as a function of shear angle q   for zero plasma velocity ( V = 0 ) and different pairs of normalized curvature radii and normalized wave numbers: (a)  R/a = 40, k a = 0.6; (b)  R/a = 160, k a = 0.15; (c)  R/a = 40, k a = 0.15; (d)  R/a = 160, k a = 0.6. The ratio of the field strengths is equal to 1: n = B₁/B₂ = 1. The curves denoted by (1) correspond to the model [Rezenov and Maltsev, 1994], which deals with the instability growth rate just for one boundary ( F₁ ), imposing the relation between B₀ and B₁:

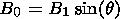(31)

In our model, we impose another relation between B₀ and B₁:

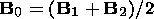(32)

Thus the magnetopause magnetic field is determined as the vector average of the magnetosheath and magnetosphere magnetic fields. This relation seems to be more reasonable because it is symmetric with respect to the fields B₁ and B₂.

In Figure 2, the curves (2) correspond to our solution of the instability problem with one boundary, while the curves denoted by number (3) correspond to our solution of the problem with two boundaries.

Comparing curves 1 and 2 in Figure 2, one can see that both models have practically the same maximum growth rate corresponding to the antiparallel magnetic fields. However, the angle interval of the instability in our model is twice larger than that in the model [Rezenov and Maltsev, 1994]. This is caused by the difference in relations (31) and (32) used in the models.

Comparison of curves 2 and 3 shows that an increase of either wave number or layer thickness makes the instability stronger, but the angle interval of the instability becomes smaller, and curves 2 and 3 become closer to each other. As one can see from the plots, an increase of the curvature radius brings about a decrease of both the maximum growth rate and the angle interval of instability. A finite thickness of the layer diminishes the maximum growth rate and increases the shear angle interval.

Figure 3

Figure 4

Figure 5

Figures 3, 4, and 5 correspond to the problem with two boundaries and nonzero plasma velocity ( U ). The magnetic field vectors B₁ and B₂ are assumed to be antiparallel at the magnetopause, and the ratio of field strengths B₁/B₂ is varied in a range 0.5-1.

Figure 3 corresponds to the ratio B₁/B₂ = 1. This figure shows the instability growth rate as a function of the velocity angle a for the different normalized plasma speeds U/U_a2: 0, 0.5, 1, 1.5, and as well for different pairs (k,R) of normalized wave numbers and curvature radii. Figures 3a, 3b, 3c, and 3d correspond to the four pairs of (k a, R/a): (0.6, 40), (0.6, 160), (0.15, 40), (0.15, 160), respectively.

As one can see in the plots, an increase of the plasma velocity in the direction perpendicular to the magnetic field causes an enhancement of the instability growth rate. On the other hand, an increase of plasma velocity directed along the magnetic field diminishes the instability growth rate.

Comparing Figures 3a and 3b as well as 3c and 3d, we conclude that the instability growth rate is larger for smaller curvature radius. The latter is more pronounced for lower velocity.

Comparing plots a and c, as well as b and d, we see that the instability growth rate is smaller for smaller wave numbers.

Comparison of plots a and d shows that the growth rate is strongly dependent on the layer thickness a for the constant values k and R. A decrease of the thickness of the layer brings about a substantial decrease of the instability growth rate.

The plots of Figures 4 and 5 are similar to those of Figure 3 but correspond to the smaller values of the magnetosheath magnetic field strength with respect to the geomagnetic field: B₁/B₂ = 0.75, 0.5, respectively. The general feature is that a decrease of the magnetosheath magnetic field leads to a diminishing of the instability growth rate. In the particular case of n = 0.5, the instability growth rate vanishes for all three values of velocity directed parallel to the magnetic field.

Conclusions

The growth rate of the interchange instability is studied as a function of the magnetic shear angle, the thickness of model magnetopause, the wave vector, and the tangential velocity of plasma.

This instability is the strongest in a case of antiparallel magnetic fields at the magnetopause. The instability decreases if the magnetosheath magnetic field deviates from the direction antiparallel to the geomagnetic field. The growth rate is positive within a finite angle interval of the magnetic shear. This angle interval of the instability is rather sensitive to the relation between the magnetopause magnetic vector and those of the magnetosheath and magnetosphere regions. Determining the magnetopause magnetic field as a vector average of the magnetosheath and magnetosphere magnetic fields, we obtained the instability angle interval, which is twice larger than that in the model [Rezenov and Maltsev, 1994].

Besides the shear angle, there are four main factors that bring about an enhanced growth rate of the interchange instability at the subsolar magnetopause: (1) increase of the thickness of the magnetopause, (2) decrease of the wavelength, (3) decrease of the local curvature radius of the magnetopause, (4) plasma flow in the direction perpendicular to the magnetic field.

The instability growth rate decreases in the case of plasma flow along the magnetic field.

From the physical point of view, the results formulated above can be explained in the following way. In the case of plasma flow in the direction perpendicular to the magnetic field, the interchange instability determined by magnetic stress  B²/R is enhanced by the Kelvin-Helmholtz instability driven by the velocity shear. However, in the cases studied in our paper when the velocity is directed along the magnetic field, the Kelvin-Helmholtz instability does not exist because of the stabilizing role of magnetic stress, and the interchange instability is weakened by the centrifugal force which is proportional to the velocity squared and the curvature of the surface.

Applying the results described above to the particular case of the southward IMF, we conclude that the growth rate of the interchange instability must decrease in the meridional plane of the magnetosphere because of plasma flow along the magnetic field. On the other hand, the growth rate must increase in the equatorial plane because of plasma motion in the direction perpendicular to the magnetic field.

Taking the parameters B₂ = 60 nT, B₁ = 30 nT, n = 5  cm ^-3, a = 400 km (total width of the layer equal to 800 km), R = 10 R_E for wave lengths l = 2.6 R_E, we obtain the following estimate for the characteristic time of the instability: t = a/(gU_A) = 116 s for zero velocity, and t = 33 s for velocity U = 300 km s ^-1 directed perpendicular to the magnetic field.

The instability can evolve into a nonlinear stage, if the growth time t is much less than the time t_c of plasma convection along the dayside magnetopause. Using a rough estimate of the convection time t_c R/U, we find the ratios t/t_c 0.1 and t/t_c 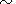0.35 for the equatorial and meridional regions of the magnetopause, respectively. This means that the perturbations caused by the interchange instability can reach a nonlinear stage at the dayside magnetopause for the southward IMF.

The interchange instability of the magnetopause seems to be an important process, which brings about the transfer of magnetic flux tubes through the magnetopause. Finally, this might cause an enhanced magnetic field diffusion at the high shear magnetopause, which in its turn can initiate the reconnection process.

Acknowledgments

This work is supported by the INTAS-ESA project 99-01277, by grant 98-05-65290 from the Russian Foundation of Basic Research, by grant 97-0-13.0-71 from the Russian Ministry of Education, by the Austrian "Fonds zur Förderung der wissenschaftlichen Forschung'' under project P12761-TPH.

References

Alexeev, I. I., and Y. P. Maltsev, Estimation of coefficient of IMF penetration in the magnetosphere as a result of development of interchange instability, Geomagn. Aeron. (in Russian), 30, 134, 1990.

Arshukova, I. L., and N. V. Erkaev, Interchange instability of the subsolar magnetopause, in The Solar Wind-Magnetosphere 3, edited by H. Biernat, C. Farrugia, and D. Vogl, pp. 191-198, Austrian Acad. of Sci., Vienna, Austria, 2000.

Chandrasekhar, S., Hydrodynamic and Hydromagnetic Stability, Univ. Press, Oxford, New York, 1968.

Freidberg, J. P., Ideal Magnetohydrodynamics, Plenum, New York, 1987.

Landau, L. D., and E. M. Lifshitz, Electrodynamics of Continuous Media, Pergamon, New York, 1960.

Luhman, J. G., R. J. Walker, C. T. Russel, N. U. Crooker, J. R. Spreiter, and S. S. Stahara, Patterns of potential magnetic field merging sites on the dayside magnetopause, J. Geophys. Res., 89, 1739, 1984.

Rezenov, B. V., and Y. P. Maltsev, Role of interchange instability in flux transfer event origin, Ann. Geophys., 12, 183, 1994.