
E. E. Antonova
Institute of Nuclear Physics, Moscow State University, Moscow, Russia
The first problem that is solved in analyzing of any plasma configuration is the problem of magnetostatic equilibrium. Plasma begin to move with great velocity if the condition of magnetostatic equilibrium is not fulfilled. Change of the external conditions or the development of internal instability can lead to the destruction of magnetostatic equilibrium. It is well known that the development of plasma instabilities is the main obstacle for solving the problem of thermonuclear fusion. Plasma motions lead to plasma cooling due to interaction with the walls of the chamber. Space plasma configurations, as a rule, have no walls. The velocity of plasma motion in many space plasma objects is much smaller than Alfvén and sound velocity. So the condition of magnetostatic equilibrium (forces connected with the existence of plasma gradients are compensated by the Amper force) is fulfilled in such objects. In spite of more then 40 years of near-Earth space plasma investigations, the problem of the creation and support of magnetostatic equilibrium in the Earth's magnetosphere continue to attract attention and have remained unsolved until now. The situation is especially surprising now that proof of the existence of the rather high level of magnetospheric plasma sheet turbulence has been obtained. The existence of such turbulence is quite natural as the solar wind plasma flow around the Earth has high fluid and magnetic Reynolds numbers. In such a case the turbulent wake must be formed. It is necessary to understand why, in contrast to laboratory plasma, such turbulence does not destroy the plasma sheet, which is constantly observed when the interplanetary magnetic field (IMF) has southward orientation. Also the explosion-like processes of local plasma heating and plasmoid formation during magnetospheric substorm do not lead to plasma sheet destruction. The plasma sheet restores its slab configuration after substorm comparatively quickly. The real changes of the configuration of the plasma sheet (plasma sheet bifurcation) take place when IMF Bz>0 and substorm activity is very weak. Such changes are accompanied with tail-lobe filling and theta-aurora formation. So support of magnetostatic equilibrium in the plasma sheet depends on IMF orientation.
In this paper, we try to summarize the results of experimental observations of plasma sheet turbulence, some results of theoretical investigations of the properties of this turbulence, and its role in magnetospheric plasma dynamics. Many aspects of the problem discussed correspond to the point of view of the author and do not coincide with the content of existing textbooks on magnetospheric physics. But the formulated problems require the real attention of the specialists, and we hope that the material presented can be useful in attracting such attention.
The paper is organized as follows. The data of experimental observations are analyzed in Section 2. Section 3 is dedicated to the nature of observed turbulence, its spectra and the self-organized criticality (SOC) approach to analyzing the properties of magnetospheric turbulence. Section 4 summarizes arguments in support of the action of the inner magnetospheric source of dawn-dusk electric field and large-scale magnetospheric convection. We discuss the main aspects of the plasma sheet theory with medium-scale developed turbulence and compare its predictions with results of experimental observations in Sections 5 and 6. Section 7 contains conclusions and discussions.
Observations of multiple manifestations of plasma sheet turbulence began with the first systematic investigations of the polar aurora. The "sky image" of near-Earth space plasma demonstrated the presence of multiple structures moving with different, and sometimes very large, velocities (see Chamberlain [1961]). The first stages of the investigations were mainly concentrated on periods of great increases in turbulence intensity -- magnetospheric substorms. But even at this first stage it was known that the magnetosphere has its own "internal life" and that electromagnetic fluctuations are constantly observed at auroral latitudes in wide frequency ranges. Observations of the magnetic field in the geomagnetic tail beginning with the work of Ness [1965], have shown that the magnetic field can be rather regular and that magnetospheric substorms are accompanied by changes in the topology of magnetic field lines (reconnection phenomena). Such phenomena (see the review of Pudovkin and Semenov [1985]) and continue to become the main object of interest. Plasma motion in the plasma sheet was, as a rule, considered to be the laminar motion. The observed reconnection phenomena were analyzed as the result of the development of some kind of instability (spontaneous reconnection), but forced-reconnection models were also developed. At the same time it was recognized that plasma-sheet flow may occasionally be in a state of turbulence (see Swift [1977, 1981]; Trakhtengerts and Feldstein [1987]).
The widely used picture of the existence of the laminar plasma sheet could be changed when multiple measurements of the electric field on the auroral field lines and in the plasma sheet became possible. Such measurements (see Maynard et al. [1982]; Mozer et al. [1980]; Weimer et al. [1985]) and later results of Viking, Freja, Fast satellites have shown that electric fields at auroral field lines are much stronger than the large-scale, dawn-dusk electric field and also highly turbulent. The results of auroral plasma measurements also clearly demonstrated the possibility of the existence of nonequipotential magnetic field lines. First results of auroral and plasma sheet electric field observations were summarized by Antonova [1985]. It was shown that in the conditions of the existence of field-aligned electric fields, observed fluctuations of the electric field lead to nonconservation of particles in the magnetic flux tube and intense plasma sheet mixing. The results obtained closed the "convection crisis problem" formulated by Ericson and Wolf [1980]. This problem appeared in theoretical works that postulated that particles in the magnetic flux tube are conserved in the process of flux tube convection from the far-tail to the near-tail regions. The existence of fluctuating electric fields, amplitudes of which are much larger than the amplitude of the dawn-dusk electric field, means that the picture of plasma flow is much more complex than has been discussed. The nonequipotentiality of magnetic field lines leads to the magnetic flux tube splitting on segments moving in different directions with different velocities. One main consequence of the existence of plasma sheet turbulence is intense plasma mixing (see Antonova [1985]). As a result of such mixing, the temperatures of the plasma sheet ions and electrons must weakly depend on latitude and longitude. The absence of the dependence of ion and electron temperatures from latitude and longitude was demonstrated by Antonova et al. [1998, 1999] on the basis of Intercosmos-Bulgaria 1300 satellite results. The comprehensive temperature distributions obtained by Wing and Newell [1998] on the basis of DMSP results support the absence of central plasma sheet ion temperature coordinate dependence. At the same time, methods of electric field measurements in the rarefied hot plasma sheet plasma were not very reliable (large values of Debye length). So, plasma transport due to the existence of medium- and small-scale electric field was not introduced in discussion of magnetospheric convection.
All models of magnetospheric convection relate its existence to the interaction of the magnetized solar wind with the Earth's magnetosphere. Multiple investigations (see, for example, the review of Marsch and Tu [1997]) have demonstrated the permanent presence of solar wind turbulence. Such turbulence can obviously create magnetospheric turbulence. The clear manifestation of the existence of low-frequency magnetospheric turbulence was obtained through spectral analysis of geomagnetic indexes (see Takalo et al. [1993]; Tsurutani et al. [1990; Uritsky and Pudovkin [1998]). Uritsky and Pudovkin [1998] have shown that the Bz component of the IMF, velocity of solar wind plasma, and the coupling function of Akasofu are insufficient factors to explain the behaviors of the AE index of geomagnetic activity. The noncoincidence of forms of Fourier-spectra of solar wind parameters and AE -fluctuation spectra means that inner magnetospheric sources of turbulent fluctuations of auroral electrojets exist and is in rather good agreement with the results of plasma sheet electric field measurements.

|
| Figure 1 |

|
| Figure 2 |
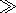 1,
where
m0 is magnetic permiability of vacuum,
p is the plasma pressure,
B is the magnetic field,
schematically shown in Figure 2, are highly turbulent. Plasma flow is
ordinary in the regions where
b
1,
where
m0 is magnetic permiability of vacuum,
p is the plasma pressure,
B is the magnetic field,
schematically shown in Figure 2, are highly turbulent. Plasma flow is
ordinary in the regions where
b 1 (tail lobes,
mapped on the polar cap, and deep ( L<5 ) inner-magnetosphere regions)
and it is of nonregular character where
b>1. The distribution of the most
turbulent magnetospheric domains makes it possible to suggest that
the main sources of inner magnetospheric turbulence are concentrated
in high
b magnetospheric regions and on the boundaries
of such
regions. Only large-scale fields partially penetrate the low
b regions. But this suggestion requires real experimental
verification.
1 (tail lobes,
mapped on the polar cap, and deep ( L<5 ) inner-magnetosphere regions)
and it is of nonregular character where
b>1. The distribution of the most
turbulent magnetospheric domains makes it possible to suggest that
the main sources of inner magnetospheric turbulence are concentrated
in high
b magnetospheric regions and on the boundaries
of such
regions. Only large-scale fields partially penetrate the low
b regions. But this suggestion requires real experimental
verification.
The nature of observed turbulence is not yet clear. According to Antonova et al. [[2000]; Borovsky et al. [1997]; and Yermolaev et al. [[2000], plasma sheet velocity fluctuation correlation times (~2 min) are much larger than the correlation times of magnetic field fluctuations (~10 min). The results of Troshichev et al. [[2000] clearly demonstrate the inconsistency of magnetic field and plasma velocity variations even in the distant plasma sheet. Therefore, plasma sheet turbulence is not MHD turbulence. The difference between the correlation times of velocity and magnetic field fluctuations suggests that electrostatic modes (which can more easily develop in a collisionless plasma) dominate in many cases. Particle beams formed in the process of plasmoid motion and particle acceleration in electric field fluctuations can constitute ballistic modes of the observed turbulence. The level of turbulence can evidently depend on the level of geomagnetic activity. It grows after the substorm expansion phase onset and decreases 1-2 h later (see Antonova et al. [[2000]).
Antonova and Tverskoy [1998] analyzed the role of plasma pressure gradients in generating the magnetospheric electric fields and discussed the possibility of the existence of nonlinear transport of energy between large- and medium-scale electrostatic harmonics. It was shown that the two-vortex electric field is the zero harmonic of the solution of the problem of magnetosphere-ionosphere interaction and four-vortex electric field -- the first harmonic. The generation of smaller scale harmonics in the case of the equipotential field line was analyzed by Ivanov and Pochotelov [1987] and in the case of the existence of the field-aligned potential drops by Antonova [1993]. The magnetospheric vortexes are coupled with the dissipative ionosphere (magnetosphere-ionosphere interactions). Another source of dissipation is the heating of magnetospheric particles. Horton et al. [1993] analyzed the generation of large-scale vortexes due to the development of drift instabilities and velocity shear. Powerful sources of inner magnetospheric turbulence are waves from the solar wind and magnetosheath.
Rather high levels of the observed turbulence show that it is strong. The balance of the generation of turbulence and its dissipation determines the form of spectra of the turbulence. Linear analysis can give the characteristic scales of the most unstable harmonics. Obtaining the turbulence spectra requires use of the theory of a strong turbulence, which is not well developed, or corresponding computer modelling. The difficulties of creating the necessary models are partially connected with the existence of the dynamic chaos of plasma sheet particle motion. For example, postulated in many models, magnetized motion of plasma sheet electrons is not supported by the data of experimental observations (see Antonova et al. [1999]), and it is quite possible that the existence of small-scale fluctuations of the electric field produces the stochastization of electron motion when the scale of fluctuations is of the order of the electron Larmor radius.
Information on the spectra of magnetospheric turbulence is quite limited. Gurnett and Frank [1977] presented measured spectra in a wide frequency range with broad maximum near ion gyrofrequency (1-10 Hz). Many papers contain information on spectra of geomagnetic micropulsations. Weimer et al. [1985] and Basu et al. [1988], using DE 1 and DE 2 satellite data, showed that the expansion of electric field measurements at low altitudes in the Fourier series give the Kolmogorov-type spectrum of transverse electric field fluctuations
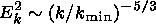 | (1) |
where k is a module of the wave vector and k min is a constant. Measurements by the DE 1 satellite at an altitude of 12,000 yielded
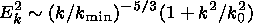 | (2) |
where k0 is a constant.
Long-period fluctuations of the geomagnetic AE index have the power spectrum f-b (where f is a Fourier frequency) with exponent b=1 at f<0.05 mHz and b>2 at higher frequencies, and they are characterized by a fractal structure stable for long intervals of moderate solar activity (see Uritsky and Pudovkin [1998]). Hoshino et al. [1994] have shown that fluctuations of the magnetic field observed in the distant plasma sheet are characterized by a "kink" Fourier power law spectrum that could be approximated by two power law functions with two different spectral indices. It was found that the power spectrum of the Bz of the magnetic field could be well fitted by
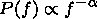 | (3) |
where
a=a1
and
0.49 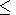 a1
a1
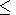 1.48 if
f<0.04 Hz,
a =a2
and
1.78
1.48 if
f<0.04 Hz,
a =a2
and
1.78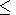 a2
a2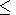 2.43 if
f>0.04 Hz.
Borovsky et al. [1997]
obtained the
occurrence distributions of plasma sheet bulk flows
P(vx) and
P(vy) in
X and
Y directions based on 53,408 measurements of flow
in the plasma sheet between 15 and 22
RE behind the Earth on the ISEE 2
satellite. They selected an isotropic distribution of flows at low
flow velocities (eddy turbulence) and an anisotropic distribution of
fast flows (BBFs). In accordance with
Borovsky et al. [1997],
2.43 if
f>0.04 Hz.
Borovsky et al. [1997]
obtained the
occurrence distributions of plasma sheet bulk flows
P(vx) and
P(vy) in
X and
Y directions based on 53,408 measurements of flow
in the plasma sheet between 15 and 22
RE behind the Earth on the ISEE 2
satellite. They selected an isotropic distribution of flows at low
flow velocities (eddy turbulence) and an anisotropic distribution of
fast flows (BBFs). In accordance with
Borovsky et al. [1997],
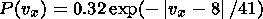 | (4) |
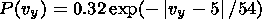 | (5) |
where vx and vy are measured in km s -1. The distribution of fast BBF flows can be fit by
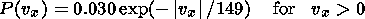 | (6) |
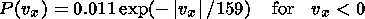 | (7) |
The study of Borovsky et al. [1997] reveals power-law spectral shapes of the time history of flows and fields, which would be consistent with turbulent spectra in k space if a random-sweeping model of the vortices is assumed.
Angelopoulos et al. [1999], using 2.8 years of GEOTAIL satellite data, studied the probability distribution functions of flows in the plasma sheet and show that they can be readily approximated with two log-normal distributions, as expected from intermittent turbulence. They argue that the presence of fast flow log-normal component in the distribution is evidence of intermittency, that is, long periods of slow flow interrupted by short-lived periods of fast convection. Angelopoulos et al. [1999] suggested that turbulent flows resemble the turbulent field adjacent to a jet and that strongly driven turbulence spreading away from the BBFs alter the fundamental process of material transport and momentum in the collisionless plasma sheet plasma by introducing an effective diffusion process.
In the physical system exhibiting self-similarities over a broad range of temporal and spatial scales, spatial scales may be described by fractal geometry, and time scales lead to 1/f -like power spectra. Bak et al. [1987, 1988] suggested that there may be an intimate connection between scale invariance in space and time as it happens at critical transitions. Because there is no externally controlled critical parameter in many natural systems, they call this basic property self-organized criticality (SOC). SOC describes systems that naturally reside far from an equilibrium state. It describe the interaction between fractal processes (fluctuations with the spectrum like f-b ) and spatial fractal structures. The ensemble average of the system is its most common state rather than steady state. Such systems, envisioned as dissipative and subject to continuous variable external driving, exhibit intermittent output that is governed by power-law spectra. The running sandpile has been used as a paradigm and simple dynamic model that exhibits these general SOC properties. An SOC model describes the dynamics of the transport without relying on the underlying local fluctuation mechanisms. Noise-driven SOC systems can maintain average profiles that are linearly stable (submarginal) and yet are able to sustain active transport dynamics. The dynamics of SOC can be computationally investigated with a cellular automata model of "running sandpile" dynamics. In such models, localized fluctuation is modeled by grid site (cell), local turbulence mechanism by automata rules, critical gradient for local instability by critical sandpile slope, local eddy-induced transport by number of grains moved if the slope is unstable, total energy/particle content by total number of grains, heating noise/background fluctuations by random rain of grains, energy particle flux by sand flux, mean temperature/density profile by average slope of sandpile, and transport event by avalanche (see Newman et al. [1996]).
From the moment of its suggestion, SOC models have been widely used to explain the forms of magnetospheric turbulence spectra as power-law spectra are a natural consequence of a system driven in a state of SOC. The effect of SOC was proposed by Uritsky and Pudovkin [1998] as an internal mechanism to generate f-b fluctuations of geomagnetic intensity. It was shown that power spectrum of sandpile model fluctuations controlled by real solar wind parameters reproduce spectral features of the AE fluctuations. The origin of f-b fluctuations in nonequilibrium systems with many degrees of freedom was connected with the superposition of numerous instabilities with the large relaxation time range. Zelenyi et al. [1998] have shown that the form of magnetic field fluctuation spectra in the far tail region can be explained if the turbulence has a fine fractal structure. Angelopoulos et al. [1999] have shown that many features of tail velocity fluctuation spectra can be explained using the SOC approach. The latest substorm models of Sitnov et al. [[2000] and Klimas et al. [[2000] are based on SOC hypothesis.
At the same time, in spite of the great popularity of SOC models, they cannot comprehensively explain all observed spectra. SOC hypothesis also does not solve the problem of the existence of confined, comparatively stable plasma structures (such as, for example, the plasma sheet of Earth's magnetosphere) filled with turbulent plasma. It is necessary to also mention that the values of plasma velocity fluctuation across the plasma sheet are, as a rule, smaller than the sound, and Alfvén velocities and plasma pressure distribution are near isotropic. This may suggest that the condition of magnetostatic equilibrium is fulfilled across the plasma sheet on scales larger than the characteristic dimension of plasma eddy. Later, we show that such suggestion can help solve the problem of turbulent plasma sheet formation.
One of the main features of magnetospheric convection is the existence of two large-scale electrostatic vortexes and the dawn-dusk electric field. Determination of the nature of this field is one of the main problems of the physics of the magnetosphere. Beginning with the works of Axford and Hines [1961] and Dungey [1961] it has been ordinarily suggested that dawn-dusk electric field is produced by MHD dynamo in the magnetospheric boundary layers or penetrates from the solar wind. Dungey mechanism of reconnection deposits the reverse of the magnetospheric convection from antisunward to sunward on the boundary of open and closed field lines. The results of the analysis presented by Elphinstone et al. [1991]; Feldstein and Galperin [1985]; and Galperin and Feldstein [1991] clearly demonstrated that the polar cap boundary does not coincide with the polar auroral oval boundary. The region of precipitation from the plasma sheet boundary layer is deposited between these boundaries. In accordance with multiple models of the action of MHD generator in the magnetospheric boundary layers, Region 1 currents must be mapped on the boundary layers. Boundary layers are mapped on the near cusp regions in accordance with all existing magnetic field models. The picture of Region 1 current density with maxima near 1400-1500 and 0700-1000 MLT of Iijima and Potemra [1976] was considered as the proof of this mapping. But it is necessary to mention that the published [Iijima and Potemra, 1976] distribution of Region 1 current density was missed with the distribution of integral currents. Current sheet widths in the picture of the field-aligned current distribution of Iijima and Potemra [1976] are much larger near 0600 and 1800 MLT than near 1400-1500 and 0700-1000 MLT. Thus, the integral current maxims are localized near 0600 and 1800 MLT, which is supported by radar observation data [Foster et al., 1989]. It is impossible to map 0600 and 1800 MLT regions on the boundary layers using any of the existing magnetic field models.
Region 1 current mapping on the inner magnetospheric region requires searching for the inner magnetospheric mechanism that supports such currents. Such a mechanism was suggested by Antonova and Ganushkina [1996] (see also [Antonova and Ganushkina, 1997]) and was named the magnetospheric topology mechanism. As this mechanism is not as popular as widely discussed boundary layer mechanisms, we discuss its action and try to show that this mechanism can be considered as the real candidate for dawn-dusk electric field generation.
It is well known that in conditions of magnetostatic equilibrium,
plasma pressure gradients determine the large-scale transverse
where
p is the plasma pressure,
where
b is the angular coordinate. So,
Taking into account the relation (9) we have
In accordance with (12), field-aligned current in the
magnetostatic equilibrium configuration is equal to zero if
The dependence of the dawn-dusk electric field on the
IMF orientation can be explained as the result of the
solar wind's large-scale magnetic field influence on the inner
magnetosphere's magnetic configuration. This influence will be
especially pronounced in the regions where magnetospheric magnetic
field
B is comparable with IMF
B. Such
influence is possible to see by analyzing (8). If the sign of
the externally added (in the simplest case penetrated) magnetic field
is inverse to the sign of
B in the equation (8)
and the plasma pressure gradient does not change, the external source
must lead to transverse current growth. The equation (9) shows
that transverse current change leads to the field-aligned current
change. The change of Region 1 currents naturally produces the change
of the dawn-dusk electric field. It is easy to see that the influence
of the
additional
southward
Bz<0 leads to a larger effect than the
influence of
Bz>0. For example, if
j0=|
Comparison of the well known boundary layer mechanisms of
dawn-dusk electric field generation (MHD generator in the
magnetospheric boundary layers is considered as the development of
Axford and Hines [1961]
and
Dungey [1961]
mechanisms) with "magnetospheric topology" mechanism
shows that the latter mechanism has some preference. Boundary layer
mechanisms require the existence of finite conductivity (Dungey
type mechanisms) or finite and comparatively large viscosity (Axford
and Hines type mechanisms). Such parameters cannot be directly
obtained and it is well known that their introduction in the
collisionless plasma present principal difficulties. The
"magnetospheric topology" mechanism does not require the introduction
of unmeasurable parameters. Thus, it can be verified directly if the
distribution of the magnetic field and plasma pressure is known.
The "magnetospheric topology" mechanism action requires the
field-aligned current mapping on the magnetospheric regions with high
values of plasma pressure. First measurements of field-aligned
currents (see
Zmuda and Armstrong [1974])
have
reviled the connection of these currents with the regions of real
plasma populations. Field-aligned currents were observed on the
auroral oval latitudes. Multiple later observations support the
existence of field-aligned currents only in the regions where intense
plasma precipitation take place. Region 1 currents of
Iijima and Potemra [1976]
are properly oriented to support the dawn-dusk
electric field in the polar cap. The NBZ current system in accordance
with
Iijima and Shibaji [1987],
has the reverse direction of the
Region 1 current system and supports the dusk-to-dawn distribution of
the electric field between sheets of NBZ current. This current system
is observed simultaneously with the theta-aurora type of precipitation
on the boundaries of the polar cap auroral band. Thus, NBZ currents are
also mapped on the regions filled with plasma. The appearance of such
regions in the tail lobes is the result of plasma sheet bifurcation
when IMF
Bz>0.
It is possible to verify the discussed "magnetospheric topology
mechanism" action if the distribution of
p and
W is known. The
averaged global distribution of
p was obtained by
Wing and Newell [1998]
on the basis of DMSP observations mapped on the
equatorial plane and by
DeMichelis et al. [1999]
on the basis
of AMPTE/CCE observations.
W= const isolines can be obtained using
the empirical models of the magnetic field. Such distribution was
obtained by
Antonova and Ganushkina [1995]
when they
suggested using
W= const
picture to create the coordinate
system in the high-latitude magnetosphere, which can be used to
analyze the high-latitude processes. Unfortunately,
global pictures
obtained
of the plasma pressure contain the mixture of substorm and
quiet time data. The sharp increase of the particle fluxes near
midnight during substorm expansion phase is accompanied by the
near-tail current disruption and corresponding change of
the
W= const picture
in this region (see
Antonova and Ganushkina [[2000]).
So, it
is impossible now to compare the
p and
W distribution picture. But
extracting from the pictures of
[DeMichelis et al., 1999;
Wing and Newell, 1998]
the expansion phase periods
allows this possibility. It is necessary to mention that
Kozelova et al. [1986, 1989]
have demonstrated the formation
of the substorm pressure hole near midnight that is responsible for
generating
the
Birkeland current wedge.
It is also possible to verify the "magnetospheric topology" mechanism
action using only
magnetic measurement
data.
In accordance
with (8), plasma pressure
p= const on the current line. So
the picture of rot B distribution can be used instead of
p distribution in the region where plasma pressure is near
isotropic. The empirical magnetic field models can be used for the
analysis. Most of
the currently available models are half-empirical (see
[Tsyganenko, 1990, 2000]).
Thus, its use in the suggested
analysis can meet with definite difficulties connected with the
models' current line geometry. In spite of this
difficulty,
Antonova and Ganushkina [1996a,
1996b,
1997],
in analyzing the
W= const isoline and current line distribution in
Tsyganenko 87 and Tsyganenko 87W models, have supported the possibility
of the "magnetospheric topology mechanism" action. It was shown that
the curvature of the near-tail current lines is higher than the
curvature of flux tube volume isolines. So, the distribution of
plasma pressure along
W= const
isoline must have the minimum near
midnight and the gradients of the plasma pressure must be directed
from midnight to dawn and dusk in the morning and evening hours
respectively.
One problem connected with the possibility of verifying
the "magnetospheric topology" mechanism action is the possible
difference of the current systems in the real magnetosphere and in the
magnetospheric magnetic field models. The magnetic field has minima on the
dayside field lines far from the equatorial plane (see Figure 2). So,
transverse currents in the daytime magnetosphere are concentrated far
from the equatorial plane.
Antonova and Ganushkina [[2000]
have suggested that a cut-ring current system can exist in the
high-latitude magnetosphere. Current lines of this system are
concentrated in the equatorial plane near midnight and at high
latitudes near noon. The addition of this current system changes the
topology of the current lines in the near-tail region. Correspondingly,
it will change the configuration of the flux tube volume isolines.
Future investigation will verify the importance of the "magnetospheric
topology" mechanism of magnetospheric convection but,
it is
now
possible to mention that only this mechanism can explain the
current mapping of
inner
magnetosphere Region 1.
The existence of high levels of plasma sheet turbulence require
using
the system of
transport equations averaged on the turbulent fluctuations
instead of ordinary magnetic hydrodynamics. The
problem can be solved
half-phenomenologically
by introducting
the anomalous fluxes of particles and heat. This approach is
ordinarily used in theories of anomalous plasma transport in
laboratory conditions (see, for example,
Horton [1984]).
The
system of transport equations is obtained for the averaging
fluctuating hydrodynamic values (concentration, temperature, pressure
etc.). Monographs of
Klimontovich [1990, 1999]
contain more
careful substantiation of the possibility of such averaging.
where
n is the concentration,
no is the averaged concentration,
V is the velocity,
V0 is the averaged
velocity,
D is the coefficient of quasidiffusion. The theoretical
approach developed by
Antonova and Ovchinnikov [1996, 1999]
takes into account two major effects: constant plasma sheet compression
by the dawn-dusk electric field and the diffusion of the turbulent
plasma in the direction opposite the gradient of plasma
concentration. Figure 3 illustrates the main features of the mechanism
action. Turbulent fluctuations destroy the plasma sheet. Its thickness
is constantly increased. The large-scale electrostatic dawn-dusk electric
field tries to compress the sheet just as it takes place in the
laboratory pinch compressed by the induction electric field. If the
velocity of destruction and compression are equal, the stationary
structure is formed. Quick plasma sheet mixing
equalizes the temperature across the sheet. So, it is possible to
use the approximation of constant temperature
T= const,
supported by
the data of experimental observations. The equilibrium distribution of
concentration across the plasma sheet gives the equilibrium
distribution of plasma pressure
p=nT. If the dependence of the
regular velocity and the quasidiffusion coefficient from the value of
the magnetic field is known, the condition
j =0 determines
the dependence of the plasma pressure from the magnetic field. In the
case of the one-dimensional problem
where
b=B/BL,
BL is the magnetic field in the tail lobes,
f(b)=Lvz(b)/D(b),
L=(D/vz)
Vector potential of the magnetic field
A in such a case is
The relation between the plasma pressure and the magnetic field can be
generalized to the two-dimensional case in the tail approximation
developed by
Schindler and Birn [1986]
if the plasma sheet
half-thickness
L is much smaller than the plasma sheet characteristic
length. Let
A=A(x,z) be the
y component of the vector potential.
In the two-dimensional case, if the magnetic field dependence on the
plasma pressure
p=p(A) is known, the Grad-Shafranov equation
can be solved, and in the tail approximation
field line
shape
can be determined. If the characteristic scale
dz along the
z axis is much smaller than the characteristic scale
dx along the
sheet ( dz/dx
where
p0=p0(x) is the plasma pressure at the
tail axis,
z0=z0(x), and
p[A0(x)]=p0. The profile
p0(x) is specified
on the basis of the tail lobe observations. The term diffusion is
changed to quasidiffusion as the condition of the smallness of the
turbulent vortex in comparison with the width of the plasma sheet (its
scale can constitute 0.1-0.2
Lz ) and is not fully fulfilled. The local
thickness of the plasma sheet in the developed theoretical approach is
determined by the local value of the dawn-dusk electric field and
the local value of the
quasidiffusion
coefficient.
The increase of
the large-scale field produces plasma sheet thinning, the increase of
the coefficient of the quasidiffusion -- plasma sheet thickening. If
the large-scale electric field becomes equal to zero or changes sign,
the equilibrium solution cannot be obtained and plasma sheet
configuration cannot be formed. If the distribution of the
electrostatic potential on the ionospheric altitudes and the value of
the quasidiffusion coefficient is known, the model of
Antonova and Ovchinnikov [1996, 1999]
makes it possible
to obtain the distribution of plasma in the plasma sheet at given
geocentric distances. The
Y dependence of the plasma sheet thickness
for
X=-15 RE obtained by
Antonova and Ovchinnikov [1999]
Sergeev and Lennartson [1988] and
Sergeev et al. [1994]
observed periods of steady magnetospheric convection at
IMF
Bz<0 and demonstrated the possibility of the existence
of the
quasistationary magnetospheric configurations for long periods.
It is natural to suggest that such periods can exist when the external
source of turbulence is weak and the change of the external conditions
does not interrupt the process of inner magnetosphere turbulent
spectra formation. The existence of periods of stationary
magnetospheric convection at IMF
Bz<0 can be considered as proof
of the external nature of the
tail reconnection
source
in the near-tail
region, where turbulence is mainly electrostatic. It is natural
to suggest that when the external source excites an MHD wave with
Bz<0, the amplitude of which is higher than the minimal
meaning of
Bz<0 in the plasma sheet, the loss of magnetostatic equilibrium
and a change in the magnetic topology should take place. In such a
case, we have a forced reconnection. Another possibility,
is the excitation of some kind of large-scale
electromagnetic mode in the region where the level of turbulent plasma
sheet fluctuations is decreased. The first scenario may be more
probable as it is well known (see
Akasofu [1964])
that the
substorm expansion phase begins with the brightening of the most
equatorward auroral arc. Thus, the existence of plasma sheet
turbulence can explain the substorm expansion phase onset deep inside
the magnetosphere in the regions where plasma is comparatively stable
before onset. An effective eastward ring current discussed by
Antonova and Ganushkina [[2000]
can be considered as another
possible external source that can produce a change in tail
topology.
Any
plasma pressure
increase
in the inner
magnetosphere produces the effective eastward ring current near the
equatorial edge of this increase (due to decreased westward
current). It produces the positive magnetic field distortion near the
Earth and negative magnetic field distortion in the near-tail regions.
Reconnection at the magnetopause (see
[Antonova, 2000;
Tsyganenko and Sibeck, 1994])
can be explained as a result
of inner magnetosphere current change.
Tsyganenko and Sibeck [1994]
analyzed the near-noon magnetic field distortion by the Region 1
currents,
and Antonova [2000]
discussed the role of the
effective eastward ring current. The eastward ring current produces a
negative magnetic field distortion not only in the tail region, but
also near the daytime magnetopause. Thus, its development leads to
magnetopause motion toward the Earth. Such motion is accompanied by
the motion of cusps toward the equator and by changes in the
magnetopause configuration and thus, field line reconnection at the
magnetopause.
The theory of the plasma sheet with medium scale-developed turbulence
of
Antonova and Ovchinnikov [1996]
has predicted the value
of the coefficient of diffusion across the sheet
Dzz (GSM frame of reference is used). The order of magnitude
of
Dzz was determined by the layer half-thickness
Lz and
the velocity of regular convection to the neutral sheet
Vz, so
Dzz
where
Dzz is the eddy-diffusion coefficient,
Vz rms is the fluctuating velocity,
t auto is the autocorrelation time
of the flow velocity.
For calculated
V rms=60.8 km s
-1 and
t auto=140 s,
Dzz=2.6
Experimental observational
discussed
data
clearly
demonstrate the existence of comparatively large turbulent
fluctuations in the plasma sheet. Turbulent fluctuations of the
AE index
(and naturally in
AL,
AU,
AO ),
and the electric and magnetic field are
observed at all levels of geomagnetic activity. The amplitudes of
fluctuations are increased with the increase
in turbulence. The nature
of observed turbulence has been unclear until now. It can include large-,
middle- and small-scale vortexes (eddies), bursty bulk flows, particle
beams etc. The mechanisms of
turbulence
generation
are also
unclear. Possible sources of turbulence fluctuations are plasma
pressure gradients, velocity shears, nonstable current sheets,
and nonequilibrium features of the distribution functions. The observed
turbulence can have the intermittent character and fractal structure.
In many cases, the
SOC approach to describing the observed turbulent fluctuations
makes it possible to develop a sandpile cellular
automation model that adequately reproduces the observed fluctuation
spectra. At the same time, the
analysis
presented
demonstrates the
necessity of the development of new approaches for describing
the plasma sheet.
One unresolved problem continues to be the nature
of large-scale, two-vortex magnetospheric convection and
the dawn-dusk electric field. The well-known mechanisms for its generation
by MHD-dynamo in the magnetospheric boundary layers meet with
experimental difficulty
mapping the boundary layers.
The
mechanism
discussed
for dawn-dusk electric field generation in
the inner magnetosphere regions due to magnetospheric topology
makes it possible to solve many of the problems of magnetospheric
dynamics, including Region 1 current mapping on the inner
magnetospheric regions, the change of magnetic field global
topology (reconnection of field lines)
when the
level of global turbulent fluctuation is high and IMF control of inner
magnetosphere dynamics when magnetosheath, boundary layer, and plasma
sheet electric fields are highly turbulent. But, naturally, as with every
new hypothesis, the suggestion of the creation of plasma pressure
gradients along flux tube volume isosurfaces due to magnetospheric
asymmetry needs careful experimental verification.
Very popular MHD models of the formation of the magnetosphere and
reconnection in the plasma sheet are based on the suggestion of
the validity of MHD with finite (real or numerical) conductivity.
They make it possible to reproduce events connected with the
generation of large-scale induction electric field. In most cases,
the effects connected with the creation of plasma pressure
gradients and finite conductivity go hand in hand. The real
difference of the published numerical MHD solutions from the real
magnetosphere is very high level of plasma turbulence in the
real magnetosphere and the existence of electrostatic electric
fields. So it is not clear what configuration will be created if
the conductivity is infinite or plasma pressure gradients do not
exist. But comparatively quick progress in
modeling
methods,
including analysis of
particle
motion
suggests the
possibility
of more comprehensive models
in the near future.
The existence of intense plasma sheet turbulence
possibly suggests a very simple explanation for substorm
expansion phase onset (brightening of the most equatorial auroral) deep
inside the magnetosphere. It is natural to argue that only the region,
which was stable before substorm expansion phase onset, can become
unstable. In accordance with the data of experimental observations,
this region is situated near the inner plasma sheet boundary.
The existence of intense velocity fluctuations across the plasma sheet
in
z direction was necessary to bring them in line with well developed
slab-type plasma sheet geometry. The
first attempt in this direction
discussed
is based on the hypothesis of the formation of turbulent
electrostatic pinch compressed by dawn-dusk, large-scale electrostatic
field. The theory of plasma sheet with medium-scale developed
turbulence suggests the simple explanation of plasma sheet thinning
during substorm growth phase (due to dawn-dusk electric field
increase) and plasma sheet thickening during substorm expansion phase
(due to increase of the amplitudes of fluctuations). The value of the
coefficient of quasidiffusion was theoretically predicted 2 years
before the first published value of such coefficient and
agrees well with the results of experimental observations.
It is necessary to mention also that the
approach
discussed
has the
real possibility of direct verification. It is based on rather
simple relations that do not contain unmeasurable parameters such
as, for example, finite conductivity or finite viscosity in the
collisionless plasma. Simultaneous measurements of the magnetic field
and plasma pressure in the multi-satellite projects
could provide better verification
than was done on the basis
of the discussed analysis. The investigation of the turbulent
properties of
Earth's
magnetosphere
may be rather interesting
not only
in relation to physics of the magnetosphere, but also to plasma
physics and astrophysics. Only first steps in such investigations were
done until now.
The near future may bring
exiting results in this direction.
Akasofu, S.-I.,
The development of the auroral substorm,
Planet. Space Sci., 12 (2),
273,
1964.
Angelopoulos, V.,
W. Baumjohann, C. F. Kennel, F. V. Coroniti, M. G.
Kivelson, R. Pellat, R. J. Walker, H. Lühr,
and G. Pashmann,
Bursty bulk flows in the inner central plasma sheet,
J. Geophys. Res., 97 (A4), 4027,
1992.
Angelopoulos, V., et al.,
Characteristics of ion flow in the
quiet state of the inner plasma sheet,
Geophys. Res. Lett., 20 (16), 1711,
1993.
Angelopoulos, V., et al.,
Multipoint analysis of a bursty bulk flow event on April 11, 1985,
J. Geophys. Res., 101 (A5), 4967,
1996.
Angelopoulos, V., T. Mukai, and S. Kokubun,
Evidence for intermittency
in Earth's plasma sheet and implications for self-organized
criticality,
Phys. Plasmas, 6 (11), 4161,
1999.
Antonova, E. E., Nonadiabatic diffusion and equalization of
concentration and temperature in the plasma layer of the magnetosphere
of the Earth,
Geomagn. Aeron. (Engl. Transl.), 25 (4), 517,
1985.
Antonova, E. E.,
The development of initial substorm expansion phase
disturbance due to generation of localized electric fields in the
region of maximum upward field-aligned current,
Adv. Space Res., 13 (4), 261,
1993.
Antonova, E. E., Large scale magnetospheric turbulence and the topology
of magnetospheric currents,
Adv. Space Res., 25 (7/8), 1567,
2000.
Antonova, E. E., and N. Yu. Ganushkina,
On deciding on the coordinate
system for describing magnetostatically equilibrated regions of the
magnetosphere,
Geomagn. Aeron. (Engl. Transl.), 34 (4), 479,
1995.
Antonova, E. E., and N. Yu. Ganushkina,
Effect of the interplanetary
magnetic field on the generation of large-scale field-aligned
currents,
Geomagn. Aeron. (Engl. Transl.), 35 (6), 752,
1996a.
Antonova, E. E., and N. Yu. Ganushkina,
Geometry of the magnetic field
of the Earth's magnetosphere and generation of field-aligned
currents,
Geomagn. Aeron. (Engl. Transl.), 35 (5), 605,
1996b.
Antonova, E. E., and N. Yu. Ganushkina,
Azimuthal hot plasma pressure
gradients and dawn-dusk electric field formation,
J. Atmos. Solar-Terr. Phys., 59 (11), 1343,
1997.
Antonova, E. E., and N. Yu. Ganushkina,
Inner magnetospheric currents
and their role in the magnetosphere dynamics,
Phys. Chem. Earth (C), 25 (1-2), 23,
2000.
Antonova, E. E., and I. L. Ovchinnikov,
The equilibrium of turbulent
current sheet and the current sheet of the Earth's magnetotail,
Geomagn. Aeron. (in Russian), 36 (5),
7,
1996.
Antonova, E. E., and I. L. Ovchinnikov,
Magnetostatically equilibrated
plasma sheet with developed medium scale turbulence: Structure and
implications for substorm dynamics,
J. Geophys. Res., 104 (A8), 17,289,
1999.
Antonova, E. E., and B. A. Tverskoy,
On the nature of electric fields in
the Earth's inner magnetosphere (a review),
Int. J. Geomagn. Aeron., 1 (1), 9,
1998.
Antonova, E. E., I. L. Ovchinnikov, and Yu. I. Yermolaev,
The
coefficient of the diffusion in the plasma sheet during substorm:
INTERBALL/Tail observations,
Proc. Fifth International Conference on Substorms, St. Petersburg, Russia,
16-20 May 2000, pp. 141-144, 2000.
Antonova, E. E., M. V. Stepanova, M. V. Teltzov, and B. A. Tverskoy
Multiple inverted-V structures and hot plasma pressure gradient
mechanism of plasma stratification,
J. Geophys. Res., 103 (A5), 9317,
1998.
Antonova, E. E., M. V. Stepanova, E. V. Vikhreva, I. L. Ovchinnikov,
and M. V. Teltzov, Generation of unmagnetized motion of plasma sheet
electrons and its possible causes,
J. Geophys. Res., 104 (A9), 19,941,
1999.
Antonova, E. E., E. A. Vichreva, I. L. Ovchinnikov, M. V. Stepanova,
and M. V. Teltsov,
Chaotic character of plasma sheet particle motion:
Data of observations and theoretical analysis,
Geomagn. Aeron. (in Russian), 38 (6), 27,
1998.
Axford, W. C., and C. O. Hines,
A unifying theory of high latitude
geophysical phenomena and geomagnetic storms,
Can. J. Phys., 39 (10), 1433,
1961.
Bak, P., C. Tang, and K. Wiesenfeld,
Self-organized criticality: An
explanation of
1/f noise,
Phys. Rev. Lett., 59, 381,
1987.
Bak, P., C. Tang, and K. Wiesenfeld,
Self-organized criticality,
Phys. Rev. A, 38 (1), 364,
1988.
Basu, Sana., Sant. Basu, E. McKenzil, P. F. Faugere, W. R. Coley,
N. C. Maynard, J. D. Winningham, M. Sugiura, M. B. Hanson,
and W. R.
Hoegy,
Simultaneous density and electric field fluctuation spectra
associated with velocity shears in the auroral oval,
J. Geophys. Res., 93 (25), 115,
1988.
Baumjohann, W.,
Fast flows, braking, and dipolarization,
Proc. Fifth International Conference on Substorms, St. Petersburg, Russia, 16-20
May 2000, pp. 363-366, 2000.
Borovsky, J. E., R. C. Elphic, H. O. Funsten, and M. F. Thomsen,
The
Earth's plasma sheet as a laboratory for turbulence in
high-
b MHD,
J. Plasma Phys., 57, 1,
1997.
Borovsky, J. E., M. F. Thomsen, and R. C. Elphic,
The driving of the
plasma sheet by the solar wind,
J. Geophys. Res., 103 (A8), 17,617,
1998.
Chamberlain, J. W.,
Physics of the Aurora and Airflow,
777 pp.,
Academic Press,
New York and London, 1961.
De Michelis, P., I. A. Daglis, and G. Consolini,
An average image of
proton plasma pressure and of current systems in the equatorial plane
derived from AMPTE/CCE-CHEM measurements,
J. Geophys. Res., 104 (A12), 28,615,
1999.
Dungey, J. W.,
Interplanetary magnetic field and auroral zone,
Phys. Rev. Lett., 6 (1), 47,
1961.
Elphinstone, R. D., D. Hearn, J. S. Murhree, and L. L. Cogger,
Mapping
using the Tsyganenko long magnetospheric model and its relationship
to Viking auroral images,
J. Geophys. Res., 96 (A2), 1467,
1991.
Ericson, C. M., and R. A. Wolf,
Is the steady convection possible in the
Earth's magnetotail,
Geophys. Res. Lett., 7 (11), 897,
1980.
Feldstein, Ya. I., and Yu. I. Galperin,
The auroral luminosity structure
in the high-latitude upper atmosphere: Its dynamics and relationship to the
large-scale structure of the Earth's magnetosphere,
Rev. Geophys., 23, 217,
1985.
Foster, J. C., T. Fuller-Rowell, and D. S. Evans,
Quantitative patterns
of large-scale field-aligned currents in the auroral ionosphere.
J. Geophys. Res., 94 (A3), 2555,
1989.
Galperin, Yu. I., and Ya. I. Feldstein,
Auroral luminosity and its relationship
to magnetospheric plasma domains,
Auroral Physics, edited by
C. I. Meng, M. J. Rycroft, and L. A. Frank,
pp. 207-222, New York,
Cambridge,
1991.
Gurnett, D. A., and L. A. Frank,
A region of intense plasma wave
turbulence on auroral field lines,
J. Geophys. Res., 82 (3),
1031,
1977.
Hori, T., K. Maezava, Y. Sato, and T. Mukai,
Average profile of ion
flow and convection electric field in the near-Earth plasma sheet,
Geophys. Res. Lett., 27 (11), 1623,
2000.
Horton, B.,
Drift turbulence and anomalous transport, in
Base of Plasma Physics,
edited by R. Z. Sagdeev and M. N. Rozenblud,
vol. 2,
pp. 362-434,
Energoatomizdat,
Moscow,
1984.
Horton, W., J. Q. Dong, X. N. Su, and T. Tajima,
Ion mixing in the
plasma sheet boundary layer by drift instabilities,
J. Geophys. Res., 98 (A8), 13,375,
1993.
Hoshino, M., A. Nishida, T. Yamamoto, and S. Kokubun,
Turbulent
magnetic field in the distant magnetotail: Bottom-up process of
plasmoid formation,
Geophys. Res. Lett., 21, 2935,
1994.
Iijima, T., and T. A. Potemra,
The amplitude distribution of
field-aligned currents at northern high latitudes observed by Triad,
J. Geophys. Res., 81 (13), 2165,
1976.
Iijima, T., and T. Shibaji,
Global characteristics of northward
IMF-associated (NBZ) field-aligned currents,
J. Geophys. Res., 92, 2408, 1987.
Ivanov, V. N., and O. A. Pohotelov,
The flute instability in the plasma
sheet of the magnetosphere of the Earth,
Plasma Phys. (in Russian), 13 (12), 1446,
1987.
Kennel, C. F.,
Convection and Substorms (Paradigms of Magnetospheric Phenomenology),
408 pp.,
Oxford University Press, New York, 1995.
Klimas, A. J., J. A. Valdivia, D. Vassiliadis, D. N. Beker, M. Hess,
and J. Takalo,
Self-organized criticality in the substorm phenomenon
and its relation to localized reconnection in the magnetospheric
plasma sheet,
J. Geophys. Res., 105 (A8), 18,765,
2000.
Klimontovich, Yu. L.,
Turbulent Motion and the Structure of Chaos. The New Approach to the Statistical
Theory of Open Systems,
317 pp.,
Kluwer Academic Publishers, Dordrecht, 1990.
Klimontovich, Yu. L., Statistical Theory of Open Systems, vol. 1, 2,
Yanus-K,
Moscow,
1999.
Koshkinen, H. E. J., et al.,
Observations of plasma entry into
the magnetosphere at late magnetic local times,
Adv. Space Res., 25 (7/8), 1617,
2000.
Kozelova, T. V., J. P. Treio, A. Korth, G. Kremser, L. L. Lazutin,
A. O. Melnikov, A. Petersen, and Ya. A. Saharov,
The active phase of
substorm on the ground and satellite data,
Geomagn. Aeron. (in Russian), 26 (6), 963,
1986.
Kozelova, T. V., M. I. Pudovkin, and L. L. Lazutin,
The features of the
development of spontaneous and stimulated magnetospheric substorms on
the satellite and ground based data,
Geomagn. Aeron. (in Russian), 29 (6), 910,
1989.
Marsch, E.,
and C.-Y. Tu,
Intermittency, non-Gaussian statistics and
fractal scaling of MHD fluctuations in the solar wind,
Nonlinear Processes in Geophysics, 4 (1), 101,
1997.
Maynard, N. C., J. P. Heppner, and T. L. Aggson,
Turbulent electric
fields in the nightside magnetosphere, J. Geophys. Res., 87 (A3), 1445,
1982.
Mozer, F. S., C. A. Cattell, M. K. Hudson, R. L. Lysak, M. Temerin,
and
R. B. Torbert,
Satellite measurements and theories of low altitude
auroral particle acceleration,
Space Sci. Rev., 27 (2), 153,
1980.
Ness, N. F., The Earth's magnetic tail,
J. Geophys. Res., 70, 2989,
1965.
Newman, D. E., B. A. Carreras, P. H. Diamond, and T. S. Harm,
The
dynamics of marginality and self-organized criticality as a paradigm
for turbulent transport,
Phys. Plasmas, 3 (5),
1858,
1996.
Ovchinnikov, I. L., E. E. Antonova, and Yu. I. Yermolaev,
The
determination of the coefficient of the turbulent diffusion in the
plasma sheet on the data of INTERBALL project observations,
Kosmich. Issled. (in Russian), 38 (6), 557, 2000.
Pudovkin, M. I., and V. S. Semenov,
The Reconnection Theory and Interaction of the Solar Wind With the Earth's Magnetosphere,
Results of Researches on the International Geophysical Projects,
126 pp.,
Nauka,
Moscow,
1985.
Sandahl, I.,
The high and low-latitude boundary layers in the
magnetotail,
Interball in the ISTP Program,
edited by D. G. Sibeck and K. Kamide,
pp. 203-217, 1999.
Sergeev, V. A., and W. Lennartson,
Plasma sheet at
X
Sergeev, V. A., T. I. Pulkkinen, R. J. Pellinen, and N. A. Tsyganenko,
Hybrid state of the tail magnetic configuration during steady
convection events,
J. Geophys. Res., 99 (A12), 23,571,
1994.
Schindler, K., and J. Birn,
Magnetotail theory,
Space Sci. Rev., 44, 307,
1986.
Sitnov, M. I., A. S. Sharma, K. Papadopoulos, D. Vassiliadis,
J. A. Valdivia, A. J. Klimas, and D. N. Baker, Phase transition-like
behavior of the magnetosphere during substorms,
J. Geophys. Res., 105 (A6), 12,955,
2000.
Swift, D. W., Turbulent generation of electrostatic fields in the
magnetosphere,
J. Geophys. Res., 82 (12), 5143,
1977.
Swift, D. W., Numerical simulation of the generation of electrostatic
turbulence in the magnetotail,
J. Geophys. Res., 86, 2273,
1981.
Takalo, J., J. Timonen, and H. Koskinen,
Correlation dimension and
affinity of
AE data and bicolored noise,
Geophys. Res. Lett., 20, 1527,
1993.
Trakhtengerts, V. Yu., and A. Ya. Feldstein, Turbulent regime of
magnetospheric convection,
Geomagn. Aeron. (in Russian), 27 (2), 258,
1987.
Troshichev, O. A., E. E. Antonova, and Y. Kamide, Inconsistency of
magnetic field and plasma velocity variations in the distant plasma
sheet,
Proc. Fifth International Conference on Substorms, St. Petersburg, 16-20 May
2000,
pp. 209-221, 2000.
Tsurutani, B. T., M. Sugiura, T. Iyemori, B. E. Goldstein, W. Gonzales,
S. I. Akasofu, and E. J. Smith, The nonlinear response of
AE to the IMF
Bz driver: A spectral break at 5 hours,
Geophys. Res. Lett., 17 (3), 279,
1990.
Tsyganenko, N. A.,
Quantitative models of the magnetospheric magnetic
field: Methods and results,
Space Sci. Rev., 54 (1), 75,
1990.
Tsyganenko, N. A.,
Mapping the changeful magnetosphere: Where do we
stand? in
Proc. Fifth International Conference on Substorms, St. Petersburg, Russia,
16-20 May 2000,
p. 150,
2000.
Tsyganenko, N. A., and D. G. Sibeck,
Concerning flux erosion from
the dayside magnetosphere,
J. Geophys. Res., 99 (A7), 13,425,
1994.
Uritsky, V. M., and M. I. Pudovkin,
Low frequency
1/f -like
fluctuations of the
AE index as a possible manifestation of
self-organized criticality in the magnetosphere,
Ann. Geophys., 16, 1580,
1998.
Weimer, D. R., C. Goerts, D. A. Gurnett, N. C. Maynard, and J. L.
Burch, Auroral zone electric fields from DE 1 and 2 at magnetic
conjunctions,
J. Geophys. Res., 90 (A8), 7479,
1985.
Wing, S., and P. T. Newell,
Central plasma sheet ion properties as
inferred from ionospheric observations,
J. Geophys. Res., 103 (A4), 6785,
1998.
Yermolaev, Yu. I., A. A. Petrukovich, L. M. Zelenyi, E. E. Antonova,
I. L. Ovchinnikov, and V. A. Sergeev,
The investigation of the
structure and the dynamics of the plasma sheet in the experiment
CORALL of the project INTERBALL,
Kosmich. Issled. (in Russian), 38 (1), 16,
2000.
Zelenyi, L. M., A. V. Milovanov, and
G. Zimbardo,
Multiscale magnetic structure
of the distant tail: Self-consistent fractal approach, New Perspectives of the
Earth's Magnetotail, Geophys. Monogr., vol. 105,
pp. 321-339, 1998.
Zmuda, A. J., and J. C. Armstrong,
The diurnal flow of field-aligned
currents,
J. Geophys. Res., 79 (31),
4611, 1974.
 currents. The
presence of velocity fluctuations much smaller than Alfvén
and
sound velocity does not destroy magnetostatic
equilibrium.
In discussing large-scale currents we deal with plasma
pressure averaged on the fluctuations
(at scales much larger
than the characteristic scale of a turbulent vortex and characteristic
times much longer than the length of vortex existence). In the
high-latitude magnetosphere,
where plasma pressure is near isotropic, such
currents are equal (see the review of
Antonova and Tverskoy [1998]
and references therein).
currents. The
presence of velocity fluctuations much smaller than Alfvén
and
sound velocity does not destroy magnetostatic
equilibrium.
In discussing large-scale currents we deal with plasma
pressure averaged on the fluctuations
(at scales much larger
than the characteristic scale of a turbulent vortex and characteristic
times much longer than the length of vortex existence). In the
high-latitude magnetosphere,
where plasma pressure is near isotropic, such
currents are equal (see the review of
Antonova and Tverskoy [1998]
and references therein).

(8) 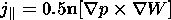
(9) 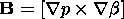
(10) 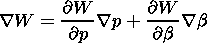
(11) 
(12) 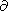 W/
W/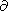 b =0 and is automatically generated if
b =0 and is automatically generated if
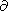 W/
W/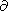 b
b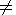 0.
0.
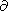 W/
W/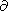 b =0 in the azimuthally symmetric configurations.
The asymmetry must
automatically lead to the generation of field-aligned currents. The
Earth's magnetosphere is azimuthally symmetric in the deep inner
magnetosphere regions where the Earth's magnetic field is near the
dipole field and highly asymmetric at the auroral latitudes. In the
far tail regions the dependence of the flux tube volume on the
angular coordinate becomes weaker, which leads to the decrease in
field-aligned current
intensity. Thus, only the transition region
from the dipole to highly tailward stretched field lines becomes the
source of field-aligned current.
b =0 in the azimuthally symmetric configurations.
The asymmetry must
automatically lead to the generation of field-aligned currents. The
Earth's magnetosphere is azimuthally symmetric in the deep inner
magnetosphere regions where the Earth's magnetic field is near the
dipole field and highly asymmetric at the auroral latitudes. In the
far tail regions the dependence of the flux tube volume on the
angular coordinate becomes weaker, which leads to the decrease in
field-aligned current
intensity. Thus, only the transition region
from the dipole to highly tailward stretched field lines becomes the
source of field-aligned current.
 p| /Bz0
and
dBz=0.9Bz0,
then disturbed
j=10j0 if
dBz<0 and disturbed
j
p| /Bz0
and
dBz=0.9Bz0,
then disturbed
j=10j0 if
dBz<0 and disturbed
j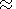 0.5j0 if
dBz>0.
It is clear that the real process
of inner
magnetospheric magnetic field
change
under the influence of IMF is the
complex nonlinear problem. The increase of current in one part of the
magnetosphere produces
magnetic field
change
in its other
parts. The inner magnetospheric magnetic field change
affects the pressure balance of the magnetopause and the
Chapman-Ferraro currents. It is necessary to mention that this change
will be accompanied by transport of the magnetic flux between the
daytime and nighttime parts of the magnetosphere. The reconnection
of field lines near magnetopause in such a case will be the
consequence, but not the cause, of the change in the magnetospheric
magnetic field. The energy deposited in the magnetosphere in the
linear approximation is proportional to the flux of solar wind
electromagnetic energy and strongly depends on the angle between the
solar wind magnetic field and the directions of the
magnetospheric current
flow.
0.5j0 if
dBz>0.
It is clear that the real process
of inner
magnetospheric magnetic field
change
under the influence of IMF is the
complex nonlinear problem. The increase of current in one part of the
magnetosphere produces
magnetic field
change
in its other
parts. The inner magnetospheric magnetic field change
affects the pressure balance of the magnetopause and the
Chapman-Ferraro currents. It is necessary to mention that this change
will be accompanied by transport of the magnetic flux between the
daytime and nighttime parts of the magnetosphere. The reconnection
of field lines near magnetopause in such a case will be the
consequence, but not the cause, of the change in the magnetospheric
magnetic field. The energy deposited in the magnetosphere in the
linear approximation is proportional to the flux of solar wind
electromagnetic energy and strongly depends on the angle between the
solar wind magnetic field and the directions of the
magnetospheric current
flow.
5. The Existence of the Quasi-Stable
Plasma Sheet and Possible Causes
of the Magnetospheric
Reconnection
Two main problems that arise in view of a high level of plasma sheet
turbulence are the existence of a quasi-stationary plasma sheet
geometry and the nature of observed reconnection phenomena. The
turbulent magnetospheric plasma sheet has the comparatively stable
equilibrium configuration.
Antonova and Ovchinnikov [1996, 1999]
suggested an explanation of the observed phenomena. The model
of
Antonova and Ovchinnikov [1996, 1999]
was developed under
the assumption that the regular plasma transport related to the
dawn-dusk electric field is compensated by quasidiffusive
transport related to the existence of turbulent transport that is, the
integral flux is equal to zero
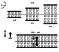
Figure 3
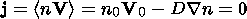
(13) 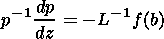
(14)  B=BL,
D is the
coefficient of quasidiffusion or eddy diffusion,
L is the plasma
sheet half-thickness. The actual dependence of
vz and
D in the
plasma sheet, where particle motion can be demagnetized, is not
known. The dependence
p(b) is determined only by their relation. For
example, if the correlation time of turbulent fluctuations
t= const,
and the value of the regular velocity and turbulent
fluctuations
B=BL,
D is the
coefficient of quasidiffusion or eddy diffusion,
L is the plasma
sheet half-thickness. The actual dependence of
vz and
D in the
plasma sheet, where particle motion can be demagnetized, is not
known. The dependence
p(b) is determined only by their relation. For
example, if the correlation time of turbulent fluctuations
t= const,
and the value of the regular velocity and turbulent
fluctuations
 B-1 (just as in the case
of electrostatic
drift),
f(b)
B-1 (just as in the case
of electrostatic
drift),
f(b)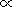 b, and we have a Harris-type
solution
b, and we have a Harris-type
solution
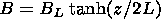
(15) 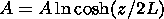
(16) 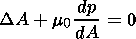
(17) 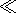 1 ), the solution of (17) has the form
1 ), the solution of (17) has the form
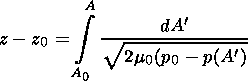
(18)
is shown in Figure 4.
The Volland-Stern model for distribution of the
electric field at ionospheric altitudes and Tsyganenko 87W model
for such distribution mapping were used to obtain plasma pressure
profiles at different IMF
Bz values. In agreement with Figure 4,
the form of the plasma sheet when IMF
Bz<0 is concave. If
Bz>0 it is
possible to see the bulge in the center of the structure. The
appearance of such a bulge
makes it possible to formulate the
hypothesis on the nature of plasma sheet bifurcation and a
theta-aurora formation at IMF
Bz>0. If the small plasma bulge is
formed in the first stage of the process,
ion and
electron
drift motion
results in the appearance of the polarization charges on the
borders of the plasma bulge. The charges produce a dusk-to-dawn
polarization electric field. Hence, the dawn-to-dusk electric field in
the bulge region decreases and can even change its sign. Such a
decrease
thickens
the local plasma sheet,
and the bulge
increases in size. If the electric field changes its sign, the plasma
sheet structure acquires the form of the Maltese cross. This structure,
mapped to the ionosphere resembles a tongue that originates near
midnight and crosses the polar cap. The electric field in the tongue
has the dusk-to-dawn direction, which corresponds to sunward
convection in the polar cap. Thus, in accordance with
Antonova and Ovchinnikov [1999],
the plasma sheet can be stable
if IMF
Bz<0. If IMF
Bz>0, the plasma sheet becomes unstable,
magnetospheric lobes are filled by plasma
from the
plasma
sheet,
and a
theta-aurora is formed. The instability of the magnetospheric
configuration at IMF
Bz>0 exists for a long time period
(~10 hours) and results in the disappearance of the high latitude
magnetospheric gradients and the auroral oval. So, when IMF
Bz>0,
the stable magnetosphere will have no plasma sheet and tail lobes. In
such conditions, the auroral oval should transform into a circle filled
with precipitation. Such a case was observed on 11 January 1997, and
was analyzed by
Koshkinen et al. [[2000].
Figure 4
6. Plasma Sheet Coefficient of Quasidiffusion
 Vz
Lz. The distribution of
Dzz across the sheet was determined by the selected dependence
of the
regular velocity and quasidiffusion coefficient on the magnetic field.
The data of ISEE 2 observations were used by
Borovsky et al. [1997]
to calculate
hydrodynamic velocity
fluctuations
and their correlation times in
X and
Y directions. A statistical
analysis of the flow velocities
Vx and
Vy in the magnetotail
plasma sheet finds two populations: a population of fast flows in the
Vz
Lz. The distribution of
Dzz across the sheet was determined by the selected dependence
of the
regular velocity and quasidiffusion coefficient on the magnetic field.
The data of ISEE 2 observations were used by
Borovsky et al. [1997]
to calculate
hydrodynamic velocity
fluctuations
and their correlation times in
X and
Y directions. A statistical
analysis of the flow velocities
Vx and
Vy in the magnetotail
plasma sheet finds two populations: a population of fast flows in the
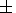 Vx directions (bursty
bulk flows) and a population of slower,
turbulent flows that are near isotropic in
Vx and
Vy. Flows
in the
z direction were not measured in that study. For evaluation
of
Dzz,
Borovsky et al. [1998]
have suggested
that turbulent flows are quasi-isotropic and measured statistical
properties of the
Vy have been used for
Vz flows.
Dzz was calculated in accordance with the relation
Vx directions (bursty
bulk flows) and a population of slower,
turbulent flows that are near isotropic in
Vx and
Vy. Flows
in the
z direction were not measured in that study. For evaluation
of
Dzz,
Borovsky et al. [1998]
have suggested
that turbulent flows are quasi-isotropic and measured statistical
properties of the
Vy have been used for
Vz flows.
Dzz was calculated in accordance with the relation

(19)  105 km
2 s
-1.
Borovsky et al. [1998]
have suggested that
Dzz reduced
till zero near the plasma sheet boundary layer.
105 km
2 s
-1.
Borovsky et al. [1998]
have suggested that
Dzz reduced
till zero near the plasma sheet boundary layer.
The
INTERBALL/Tail observation
data
(see
[Ovchinnikov et al., 2000])
allow the
plasma
sheet distribution functions in
Y and
Z directions
to be measured
every 2 min, to obtain
Dzz and compare it with theory predictions. Figure 5
compares calculated
Dzz (dashed lines) with
the theoretical predictions of
Antonova and Ovchinnikov [1996]
(solid lines) and results obtained by
Borovsky et al. [1998]
(dashed line). It is possible to see that the evaluations of
Dzz based on the theory of
medium-scale
plasma sheet
developed turbulence
agree closely with experimentally observed
values of the plasma sheet quasidiffusion coefficient.

Figure 5
7. Conclusions and Discussion
Acknowledgments
This work was supported in part by INTAS and RFBR grants, the
program Universities of Russia.
References
 20
RE
during steady magnetospheric convection,
Planet. Space Sci., 36 (2), 353,
1988.
20
RE
during steady magnetospheric convection,
Planet. Space Sci., 36 (2), 353,
1988.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on December 6, 2002.