Some problems of magnetosheath physics

M. I. Pudovkin, S. A. Zaitseva, L. L. Lebedeva, and A. A. Samsonov

St. Petersburg State University, St. Petersburg, Russia

B. P. Besser

Space Research Institute, Austrian Academy of Sciences, Graz, Austria

C.-V. Meister

Astrophysical Institute Potsdam, Potsdam, Germany

Contents

Abstract

1. Introduction

Experimental data on the solar wind flow around the Earth, other planets, and some comets show that in front of the streamlined obstacle, there appears a region of compressed and heated plasma (magnetosheath). The importance of the magnetosheath in the solar wind's interaction with the magnetosphere of the Earth or with an interplanetary magnetic cloud has been gradually recognized during the last decade. So, it is well known that the state of the magnetosphere is determined by the parameters of the solar wind. But these parameters are greatly modified on crossing the bow shock and on flowing through the magnetosheath to the magnetopause, and without knowledge of those changes, it is impossible to estimate solar wind plasma and magnetic field parameters in the magnetopause vicinity and, correspondingly, to predict the state of the magnetosphere.

One of the characteristic features of the magnetosheath and of the shocked regions in the solar wind is a relatively rapid increase of the magnetic field intensity from the bow shock to the magnetopause, which results in a remarkable plasma temperature anisotropy there. This, in turn, provides conditions for the development of various plasma instabilities. Thus, the magnetosheath may be considered as a huge, natural plasma laboratory that provides extremely high space and time resolution.

In particular, in this paper, we intend to summarize the following problems through brief results of studies:

(a) main features of various magnetosheath magnetohydrodynamic (MHD) models;

(b) the rate of the proton pitch-angle diffusion in various magnetosheath regions;

(c) influence of the proton temperature anisotropy on the magnetosheath parameters;

(d) magnetic barrier parameters in dependence on the interplanetary magnetic field (IMF) orientation.

2. Isotropic MHD Models

A steady-state flow of an ideal, perfectly conductive, isotropic plasma around the magnetosphere may be described by the standard system of MHD equations:

equation of motion:

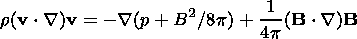(1)

equation of state:

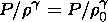(2)

(for an adiabatic flow of an electron/proton plasma g=5/3 );

equation of the frozen-in magnetic field

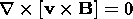(3)

equation of the solenoidity of the magnetic field:

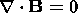(4)

and equation of the plasma continuity

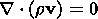(5)

This system of non-linear equations is rather complicated and is usually solved under certain simplifying suppositions.

A first magnetosheath model was developed by Spreiter et al. [1966] and Alksne [1967]. In this model, the plasma flow around the magnetosphere was calculated in a gasdynamic approximation with B=0, and then the magnetic field was obtained from the frozen-in condition (3) in a kinematic approximation. The results of calculations convincingly illustrate the formation of a bow shock and of a magnetic barrier in front of the magnetopause.

Zwan and Wolf [1976] considered an associated problem: having given the motion of a magnetic flux tube, they have shown that on approach to the magnetopause, the magnetosheath plasma is squeezed out of the equatorial part of the tube so that the formation of a magnetic barrier proves to be associated with the formation of a plasma depletion layer.

In papers by Pudovkin et al. [1982, 1987, 1995], a two-dimensional magnetosheath MHD model was proposed. This model is based on the following suppositions.

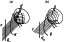
Figure 1

(a) As was shown by Pudovkin and Semenov [1977], Ampère forces, being essentially anisotropic, make the plasma flow in the magnetosheath quasi-two-dimensionally with the predominating velocity in the direction (in the Y,Z plane) perpendicular to the magnetic field lines (Figure 1a). Experimental data by Phan et al. [1996a, 1996b] seem to confirm this supposition.

We believe that this flow topology takes place for northward solar wind magnetic field.

The situation seems to change greatly in the case of a southward magnetic field. Indeed, for IMF B_z<0, because of an intensive erosion of the dayside magnetopause [Aubry et al., 1970; Fairfield, 1971; Kovner and Feldstein, 1973; Pudovkin et al., 1984, 1998; Tsyganenko and Sibeck, 1994], it flattens and becomes quasi-plane. In this case, the magnetosheath plasma flow being, as in case (a), quasi-two-dimensional, proceeds like that in the model by Parker [1973], that is, parallel to the magnetic field lines (Figure 1b). For intermediate IMF orientations, the magnetosheath plasma is supposed to spread in the direction perpendicular to the magnetopause stagnation line; the orientation of this line is supposed to depend on the IMF direction and varies from the transversal one in case of a southward IMF to the longitudinal one in case of a northward IMF [Yeh, 1976].

(b) Magnetic field reconnection at the magnetopause results in a significant change of the boundary conditions at the magnetopause: instead of the traditional conditions v_n=0 (where v_n is the normal component of the plasma velocity), there is assumed

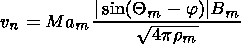(6)

where Ma_m=0.1-0.2 [Feldman, 1986] is the Alfvénic Mach number at the magnetopause; B_m is the intensity of the magnetosheath magnetic field in the magnetopause vicinity. Q_m is the angle between the magnetic field B_m and the Z -axis of the GSM coordinate system, and j determines the orientation of the reconnection line.

All the values: v_n, Q_m, j, B_m and r_m are obtained self-consistently from the solution of the corresponding system of MHD equations.

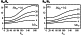
Figure 2

Figure 3

Some of the results of the model are presented in Figures 2a and 2b, and Figures 3a and 3b.

Figure 2 shows the ratio of the intensity of the magnetosheath magnetic field at the magnetopause ( B_m ) to that in the solar wind ( B_w ) as a function of the angle Q_w and the Alfvénic Mach number ( Ma_w ) in the solar wind for two values of Ma_m (Figures 2a and 2b, respectively). As one can see, this ratio increases with the increase of Q_w (that is, with IMF turning southward) and Ma_w. Furthermore, it depends on the value of the normal component of the plasma velocity at the magnetopause: the magnetic barrier intensity decreases with the increase of Ma_m.

Figures 3a and 3b present the plasma density at the magnetopause also as a function of Q_w and Ma_w for the same two values of Ma_m=0.1 and 0.2. The figures show that the depth of the plasma depletion is greatest for southward IMF and becomes less pronounced with the increase of Ma_m.

A three-dimensional model of the magnetosheath and the magnetic barrier has been developed by Erkaev [1989]. This model does not suppose any change of the magnetopause shape associated with magnetic field reconnection. Consequently, the plasma flow topology in the case of a southward IMF proves to be the same as in the case of a northward IMF. Thus, the only result of the IMF turning southward in the Erkaev model is the change in accordance with (6) of the normal component of the plasma velocity at the magnetopause. And as the v_n increases with the Q_w increase, the IMF turning southward results in the decrease of the B_m value (see Figure 2a).

The real topology of the magnetosheath plasma flow is yet unknown, and only a detailed comparison of the model predictions with experimental data may show which of those models is preferable.

However, in all the models mentioned above, the magnetosheath structure is obtained in the frame of the isotropic magnetohydrodynamic theory. At the same time, it is well known that the solar wind plasma, at least in the magnetosheath, is essentially anisotropic. Correspondingly, the results obtained for isotropic models may need some corrections. In the next sections of the paper we consider magnetosheath models obtained in the frame of the anisotropic MHD theory.

3. Anisotropic Models

3.1. Basic Equations

The flow of a highly conductive anisotropic plasma around the magnetosphere may be described by the equations of anisotropic MHD in the Chew et al. [1956] approximation as:

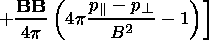(7)

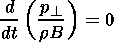(8a)

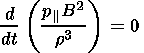(8b)

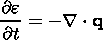(9)

where I is the unit tensor

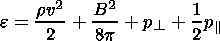and

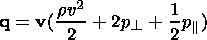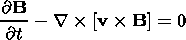(10)

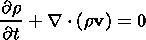(11)

Equations (8a) and (8b) represent the double-adiabatic laws and are the result of the fact that in a magnetized collisionless plasma the degrees of freedom in directions parallel and perpendicular to the magnetic field are split, so that the temperatures T  and T  vary. Combining these two equations, one obtains:

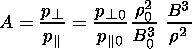(12)

The last equation shows that the pressure anisotropy has to increase rapidly with the increase of the magnetic field intensity and with the decrease of the plasma density. As the value of B in the magnetosheath increases and the plasma density decreases toward the magnetopause, one has to expect the plasma temperature anisotropy to rapidly increase across the magnetosheath.

3.2. Temperature Anisotropy Model

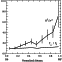
Figure 4

Experimental data on variations of the proton temperature anisotropy within the magnetosheath were investigated in detail by Hau et al. [1993], Denton et al. [1994], and Hill et al. [1995]. In Figure 4 (after Hill et al. [1995]), the variations of the proton temperature anisotropy A=T /T and of the value of B³/r² across the magnetosheath obtained by the superposed epoch method from the data of 10 magnetosheath crossings are presented. As is seen in the figure, the value of B³/r² increases across the magnetosheath by a factor of about 6. At the same time, the value of A increases only 1.3 times. This discrepancy may be explained by the existence of sufficiently intensive heat fluxes [Hau et al., 1993]. However, data on the partial polytropic indices show [Pudovkin et al., 2000a] that the sum =g +2g, at least within the inner layers of the magnetosheath, is close to 5, which supposes the plasma flow to be adiabatic. In this connection, the explanation of this disagreement by a rapid pitch-angle diffusion of the magnetosheath protons [Denton et al., 1994; Hill et al., 1995] seems to be more plausible.

The nature of the plasma wave turbulence responsible for the magnetosheath pitch-angle scattering was investigated in papers by Anderson et al. [1991], Denton et al. [1994], Gary [1992, 1993], Gary and Winske [1993], Gary et al. [1993a, 1993b, 1994a, 1994b], Hill et al. [1995], Hubert [1994], Hubert et al. [1998], Phan et al. [1994], and others.

According to Gary [1992, 1993], in an anisotropic plasma with T /T > 1, the most effectively developed two modes are the ion-cyclotron and mirror instabilities.

The threshold for the development of the mirror wave instability is determined by the expression [Hill et al., 1995]:

(13)

where b =8pp/B², and the threshold of the ion-cyclotron instability is [Gary, 1992, 1993]:

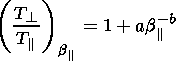(14)

where b =8pp/B², a is a factor of the order of unity, and b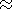0.5.

The analysis of experimental data carried out by Anderson and Fuselier [1993], Anderson et al. [1994], Denton et al. [1994, 1995], and Hill et al. [1995] shows that ion-cyclotron waves are observed most often in the plasma depletion layer in front of the magnetopause, while in the proper magnetosheath, the mirror wave turbulence is predominant.

Experimental data presented by Denton et al. [1994, 1995] show that the proton temperature anisotropy T /T closely follows the relation of the type of (14). This allowed Denton et al. [1994] to propose the "bounded anisotropy'' model, according to which no energy transfer between T  and T  takes place when T /T<(T/T)_thr, and the energy will be transferred from T  to T  to keep the temperature anisotropy at the level (T /T )_b  if T /T  approaches or trends to exceed this value.

Least-square fits of experimental data allowed Phan et al. [1994] to estimate the threshold values of T /T  as a function of b  or b  as:

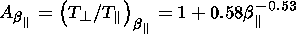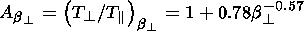However, the scatter of experimental data is rather large, and the real value of the temperature anisotropy may be significantly larger than the threshold value of (T /T )_thr. Denton et al. [1995] explain this scatter of experimental data by the dependence of the instability threshold on the varying conditions in the solar wind. However, the physical mechanism of the supposed dependence is not clear. In our opinion, the scatter of experimental data may be associated with the following factors:

(a) As it follows from (12), the variation of the proton temperature anisotropy A across the magnetosheath with the proton pitch angle diffusion being taken into account in a steady-state flow may be written as:

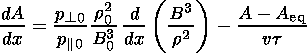(15)

where A _eq is the temperature anisotropy in the plasma in an equilibrium state, v is the plasma velocity, and t is the characteristic time of the anisotropic relaxation. Thus, the value of A is determined by the ratio of the terms corresponding to the source and the sink of the anisotropy (the first and the second terms on the right-hand side of (15), respectively). And even when the value of A _eq is a fixed function of b  or b , the first term obviously depends on the solar wind parameters.

Correspondingly, the observed value of A also has to depend on the solar wind parameters.

(b) As mentioned above, the Denton et al. [1994] model supposes that the only cause of the plasma turbulence responsible for the temperature anisotropy relaxation is the plasma instability associated with that anisotropy. However, experimental data show that the pitch-angle diffusion exists even when the observed temperature anisotropy is lower than (T /T ) _thr [Pudovkin et al., 2000a]. This allows one to suppose that there always exists a background plasma turbulence brought into the magnetosheath from the solar wind or generated at the bow shock. And as the perfectly equilibrium plasma is the isotropic plasma, we may accept A _eq=1. At the same time, the value of t is determined by the intensity of the plasma wave turbulence. Correspondingly, t may be expected to be large when A < (T /T )_thr, and relatively small when A>(T /T ) _thr.

This also contributes noticeably to the scatter of the observed values of the proton temperature anisotropy.

A theoretical estimate of the anisotropy relaxation time may be obtained only in the frame of the non-linear theory of plasma instabilities. However, this theory is poorly developed at present, and we shall try to find its value from the experimental data.

3.3. The Proton Temperature Anisotropy Relaxation Time

As it follows from (15) with A _eq=1,

(16)

(16) allows one to calculate the value of t at any point in the magnetosheath provided that the profiles of B, n, v and A are given.

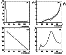
Figure 5

As the experimental data for the analysis, slightly modified profiles of B³/r² and of A presented in Figure 4 after Hill et al. [1995] were used. Corrections introduced into the experimental profiles are as follows:

• According to Sckopke et al. [1990] and Hau et al. [1993], in the close vicinity of the bow shock, the proton temperature anisotropy may amount to A=3-6; then, on moving into the sheath, it rapidly decreases (due to the ion-cyclotron instability) to A=1.1-1.2 at a distance of 0.2-0.3 R_E. This variation of A is added to the A(x) profile presented by Hill et al. [1995] (Figure 5a).
• The curve of B³/r² obtained by Hill et al. [1995] is smoothed (Figure 5b).
• As is seen from (16), to estimate the value of t, a plasma velocity profile v(x) is needed. Hill et al. [1995] do not present any data on the mean v(x) profile. Because of that, we have accepted the v(x) profile (also smoothed) of 17 November 1985, from the same paper by Hill et al. [1995] (Figure 5c).

Results of the calculations of t are shown in Figure 5d. In spite of extreme sketchiness of the obtained profile of t(x), one may distinguish three characteristic regimes:

(a) In the close vicinity of the bow shock, t is about some seconds, which suggests a rather intensive wave turbulence in this region, and the intensity of that turbulence rapidly decreases with the distance from the bow shock.

(b) In the magnetic barrier region in front of the magnetopause, the value of t is about 20 s.

(c) At the proper magnetosheath ( x=0.2-0.8 ), t gradually increases (correspondingly, the rate of the proton pitch-angle diffusion decreases) from 10 s to about 50 s, and then again decreases to about 20 s.

Taking into account results obtained earlier by Anderson and Fuselier [1993] and by Denton et al. [1994], one may suppose this behavior of t to be determined by the varying ratio of the mirror and ion-cyclotron wave turbulence with a possible influence of the background turbulence brought into the magnetosheath from the solar wind. If so, the obtained results suggest that the rate of the proton pitch-angle diffusion caused by the ion-cyclotron turbulence is significantly higher than that associated with the mirror-wave turbulence.

Of course, this problem needs a theoretical consideration.

These results allow us to assume the diffusion term in (15) as a sum of at least three terms:

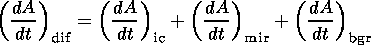(17)

where

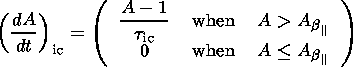results from ion-cyclotron turbulence,

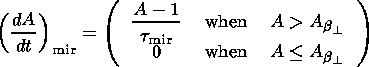results from the mirror-wave turbulence, and

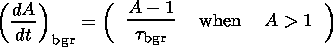is associated with the background (or external) turbulence.

3.4. Numerical Results

One of the first magnetosheath models in an anisotropic plasma approximation (a two-dimensional version) was proposed by Pudovkin et al. [1999]. This model, being a generalization of the isotropic model by Pudovkin et al. [1982, 1987, 1995], is constructed under the same suppositions and with the same boundary conditions as the latter. The locations of the magnetopause and the bow shock are fixed. The evolution of the pressure tensor components are given by (8a) and (8b), with diffusion terms in the form:

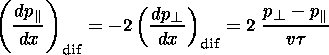(18)

Figure 6

The results of calculations for Ma_m=0.1, M_w=8 and Ma_w=10, and for two values of t (2000 s and 8 s) are presented in Figure 6.

An interval of 2000 s substantially exceeds the time taken by the solar wind plasma to cross the magnetosheath ( Dt= 500-1000 s); thus, the flow may be considered to be close to a double-adiabatic one. In contrast with this, t=8 s is much smaller than Dt, and the model corresponds to an intensive proton pitch-angle diffusion resulting in an almost isotropic proton temperature all over the magnetosheath. In front of the bow shock, the plasma is supposed to be isotropic, and the jump of the plasma and magnetic field parameters across the bow shock was calculated using the Rankine-Hugoniot conditions for an isotropic plasma; just after the bow shock, the ratio T /T  was taken to equal 1.3.

As one can see from Figure 6, the magnetic field profiles obtained for both anisotropic models prove to be rather close.

The plasma density profiles change with the variation of t more noticeably, especially for southward IMF. Indeed, while the value of r/r _sw at the magnetopause for Q _sw=60^o is about 4 for both models, for Q _sw=180^o it decreases from 3.2 for the t=8 s model to 1.2 for the model with t=2000 s. And what is even more important, the shape of the density profiles changes with the variation of t; in particular, the maximum of r/r _sw typical for all the density profiles in the t=8 s model disappears for the Q_sw > 120^o profiles in the case of t=2000 s.

And, as could be well expected and is seen in the figure, the independent variations of the perpendicular and parallel temperatures across the magnetosheath result in essentially different profiles of T  and T. The value of T /T depends on the IMF direction: it is relatively small (about 1.5-2) for Q _sw=60^o and amounts to 14 for Q _sw=180^o.

This dependence is explained by a strong dependence of the plasma density ( n ) and magnetic field intensity ( B ) profiles on the IMF orientation (compare curves 1 and 5 in the figure).

In case of a relatively intensive pitch-angle diffusion ( t=8 s), the temperatures T  and T  vary across the magnetosheath almost synchronously, and the proton temperature anisotropy is relatively small across the entire magnetosheath.

At the same time, the intensive transfer of energy from the perpendicular degrees of freedom to the parallel one causes a significant change of the temperature profiles, especially for T . As one can see in the figure, in contrast to the model with t=2000 s, where T  continuously increases from the bow shock to the magnetopause, in the case of t=8 s, T  approaches a maximum at some distance from the magnetopause and then rather rapidly decreases. The T  profiles are similar to the T  profiles.

Another version of the two-dimensional anisotropic model of the magnetosheath is presented by Denton and Lyon [[2000]. There it is supposed, as in the Erkaev [1989] model, that the flow topology is preserved for all IMF directions. However, in contrast to the Erkaev model, the magnetosheath plasma is supposed to spread from the equatorial plane along the magnetic field lines. The boundary condition for the X -component of the plasma velocity is accepted in a form: v_mp=f v _sw with f=0.125-0.25. And, finally the evolution of the proton pressure anisotropy is determined by the bounded anisotropy model [Denton et al., 1994].

Results of calculations show that the pressure anisotropy results first of all in the increase of the bow shock standoff distance. Besides, the increase of the plasma velocity at the magnetopause is shown to produce a decrease of the magnetic barrier intensity. This allowed the authors to conclude that a southward turn of the IMF followed by the increase of the plasma velocity at the magnetopause has to result in a decrease of the magnetic field intensity.

Figure 7

A three-dimensional magnetosheath model in the Chew-Goldberger-Low (CGL)-approximation was proposed by Samsonov and Pudovkin [1998, 2000] and Pudovkin and Samsonov [1999]. In Figure 7, after Samsonov and Pudovkin [1998], profiles of the normalized plasma density ( n/n_w ) and magnetic field intensity ( B/B_w ) for M_w=5 and Ma_w=10 are presented. Four curves given at each panel in the figure correspond to various forms of the diffusion term in (15).

First of all, one can see that in all the adiabatic anisotropic models, the bow shock standoff distance is noticeably larger (by about 15%) than in the isotropic model. Contrary to this result, in the double polytropic model by Hau et al. [1993] (the shaded line in the figure) this effect is not observed.

In the two-dimensional version of the model discussed above, it was found that the magnetic field intensity profile in the magnetosheath depends only weakly on the level of the proton temperature anisotropy. The same picture takes place in the three-dimensional model, too: for all three anisotropic models, the B(x) profiles are close to each other and to that of the isotropic model. The plasma density profiles n(x) seem to be more sensitive to the level of the temperature anisotropy.

Figure 8

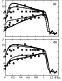
In Figure 8, after Pudovkin and Samsonov [1999], the variations of T  and T  across the magnetosheath are presented. The experimental data on T  and T  obtained by Hau et al. [1993] are given in Figure 8 by crosses and circles, respectively. Theoretical curves presented in the panel (a) are obtained for the model with the pitch-angle diffusion term in the form (model I)

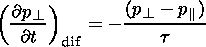for two values of t: t=1000 s (solid line) and t=300 s (dashed line). The circles in panel (b) correspond to the diffusion term in the form (model II)

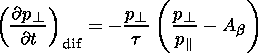with A_b=1+0.8b^-0.5  also for two values of t: t=300 s (solid curve) and t=50 s (dashed line). As is seen in the figure, all of the anisotropic models satisfactorily predict the behavior of both components of the temperature tensor; besides, one can see that for a given model, the use of a bigger t results in a higher temperature anisotropy. Concerning the two models, model II seems to agree better with experimental data than model I.

Another approach to the problem was proposed by Erkaev et al. [1999]. In that study, the magnetopause is modeled by a paraboloid of revolution; the normal components of the plasma velocity as well as of the magnetic field at the magnetopause are supposed to equal zero; the pitch-angle diffusion term is accepted in the form of the bounded anisotropy model by Denton et al. [1994]; the supposed plasma flow topology is the same as in the Erkaev [1989] model. To obtain the magnetosheath and magnetic barrier structure, the authors use the magnetic string equations, which allowed them to significantly improve the accuracy of the calculations.

The comparison of the magnetic field and plasma parameter profiles obtained for the anisotropic and isotropic models show, in reasonable agreement with the results of Samsonov and Pudovkin [1998], that the temperature anisotropy slightly enlarges the magnetosheath thickness and weakly influences the plasma density at the magnetopause.

The dependence of the magnetosheath parameters on the IMF orientation was not investigated in the three-dimensional anisotropic models. In this connection, and taking into account that B(x) and n(x) profiles weakly depend on the plasma temperature anisotropy, we shall try to interpret experimental data of the variations of the magnetosheath parameters in dependence on the IMF orientation on the base of the two-dimensional isotropic model.

4. Magnetic Barrier in the Case of the Southward IMF

As stated above, most of the magnetosheath models suppose the topology of the magnetosheath plasma flow to be independent of the IMF orientation. In particular, according to the Erkaev [1989] and Erkaev et al. [1999], models, the plasma spreads from the symmetry plane predominantly in the direction perpendicular to the magnetic field lines, while in the model by Denton and Lyon [[2000], it spreads mainly along the magnetic field lines. Correspondingly, in both models, the development of magnetic field reconnection at the magnetopause only increases the normal component of the plasma velocity at the magnetopause, and thereby decreases the magnetosheath magnetic field intensity.

In contrast to these models, Pudovkin et al. [1982, 1995, 1999] suppose the plasma flow topology to change so that in the case of a southward IMF, the symmetry plane is perpendicular to the magnetic field lines, while in the case of a northward IMF, it is parallel to the field lines (Figure 1). However, and this has to be emphasized once more, this is only a supposition; an experimental and theoretical confirmation is required. However, experimental data on the plasma flow topology within the magnetosheath are rather scarce, and one may judge the adequacy of the model mainly on the basis of indirect data, first of all, on the B(x) and n(x) profiles. But in spite of a relatively great amount of these data, they proved to be rather contradictory.

Figure 9

In Figure 9 after Pudovkin et al. [1995], there are shown (by circles) values of the magnetic field intensity at the magnetopause B_m (normalized by that in the solar wind B_w ) in dependence on the IMF direction. As the magnetosheath magnetic field strongly depends on the value of the Alfvénic Mach number in the solar wind ( Ma_w ), only crossings with 8 Ma_w20 were selected for the analysis. The solid line in the figure represents values of B_m/B_w calculated according to the model by Pudovkin et al. [1995] for Ma_w=14. The figure illustrates rather good agreement between the experimental and model data.

The variation of the B_m/B_w value with the angle Q_w predicted by the Erkaev [1989] model is shown in the figure by a dotted line. One can see that experimental data do not confirm the expected dependence of B_m on Q_w.

Figure 10

Very interesting results have been obtained by Phan et al. [1994]. Having analyzed about 40 low-latitude, dayside magnetopause crossings, the authors arrived at the conclusion that the magnetic barrier exists only in the case of a low-shear magnetopause (correspondingly, a northward IMF), and it is not observed in the case of a southward IMF (Figure 10 after Phan et al. [1994]), which seems to contradict the experimental data presented by Pudovkin et al. [1995]. Such a discrepancy between the results of various studies of the same problem and on the basis of almost the same data cannot be explained by the scatter of experimental points, and the problem needs more detailed consideration.

In this respect, let us consider concrete magnetosheath crossings presented by Phan et al. [1994] to illustrate their statistical results.

Figure 11

In Figure 11, after Phan et al. [1994], variations of the magnetosheath parameters in the magnetopause vicinity for 28 August 1984, 1300-1330 UT (a high-shear crossing according to Phan et al.) are presented. As is seen in the figure, the magnetic field intensity in the magnetopause vicinity (1305-1330 UT), in perfect agreement with the mean picture presented in Figure 9, does not exhibit any increase in front of the magnetopause. (At the same time, we have to notice that a rather deep minimum of B at 1305-1307 is not a magnetosheath structure, but a magnetopause one, peculiar for the magnetic reconnection layer), which seems to disprove the model by Pudovkin et al. [1995]. However, this conclusion proved to be erroneous. Indeed, if one considers the variation of the B(x) value across the magnetosheath on the whole, one can see a sufficiently distinct increase of B from 35 nT at the bow shock to about 65 nT at the magnetopause, which quite agrees with the definition of the magnetic barrier given by Pudovkin and Lebedeva [1987], and Pudovkin et al. [1982, 1995].

During another AMPTE/IRM satellite crossing of the magnetopause and magnetosheath on 19 September 1984, also presented in the paper by Phan et al. [1994], the magnetic shear is even higher than on 28 August. In this case, the depletion of the plasma density (from 32 cm^-3 to 22 cm^-3 ) is more evident. Besides, one can see the magnetic field intensity increase from 50 nT to 70 nT. And, according to Phan et al. [1994], the increase of the magnetic field intensity from the bow shock to the magnetopause is a typical characteristic of the magnetosheath independent from the IMF orientation. At the same time, the change of the magnetic field intensity and plasma density from the magnetosheath values to the magnetospheric values proceeds by jump, which quite agrees with the statistical picture obtained by Phan et al. [1994].

Thus, the results by Pudovkin et al. [1995] and Phan et al. [1994, 1996a, 1996b] concern quite different objects: in the first model, variations of B and n across the entire magnetosheath are considered, while the second model describes the way in which the magnetosheath parameters transfer to the magnetospheric parameters. Correspondingly, our Figure 8 shows the magnetosheath magnetic field intensity averaged for the interval about 20 min in front of the magnetopause crossing in dependence on the solar wind parameters, while Figure 9 (after Figure 9 in Phan et al. [1994]) presents the variation of the magnetic field intensity, averaged for all 40 crossings, within this 20-min interval. It seems to be obvious that these two sets of data, being so different, cannot agree nor contradict each other.

However, the variations of the magnetic field intensity and plasma density across the magnetosheath are determined not only by the value of the magnetic field shear at the magnetopause but also by the variations of the solar wind parameters, which are not known for the crossings mentioned above. Taking this into account, we consider a magnetosheath crossing that took place on 29 August 1980, and for which solar wind parameter data were available.

Figure 12

The magnetosheath profiles of the magnetic field components B_y and B_z (in the GSM coordinate system) as well as that of the total magnetic field intensity B for this crossing are presented in Figure 12 by thin solid, lines.

The solar wind data obtained onboard the IMP 8 spacecraft are shown in the figure by dashed lines.

As is seen in the figure, the IMF intensity B is almost constant for the period under consideration, while its direction significantly changes, revealing the influence of the IMF direction on the magnetosheath parameters.

The whole period of observations may be divided into three subperiods: I - from 2205 to 2240 UT, when the IMF is rather stable and essentially southward ( Q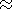-120^o ); II - from 2305 to 2340 UT, when the IMF is also stable and essentially northward ( Q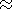40^o ); and III - from 2240 to 2305 UT - a transitional period when both the IMF intensity and orientation vary irregularly.

To take into account the influence of the IMF intensity variations on the shape of the magnetosheath magnetic field (B _sh) profile, the values of B _sh were divided by the values of B _sw with a constant time delay, t=700 s, obtained from comparing the B _sh and B _sw variations.

Figure 13

The profile of the B _sh/B _sw value is presented in Figure 13 (thick solid line). In the same figure, the profiles of B _sh/B _sw calculated according to the model by Pudovkin et al. [1995] for Ma _sw=8, Ma _mp=0.2 and for two values of Q _sw: 40^o and 120^o are given; the satellite distance from the magnetopause is given in units normalized by the magnetosheath thickness equal to 25,000 km. Besides, the variations of the angle |Q _sw|=| arctan B_y/B_z| are presented in the figure (dashed line).

In the vicinity of the magnetopause (bearing in mind the time delay t = 700 s, this period corresponds to the solar wind state during the period I), the value of B _sh/B _sw is rather close to the model curve corresponding to Q _sw = 120^o. The turn of the IMF to the north (the second period of the solar wind state) is associated with a rapid decrease of the magnetosheath magnetic field intensity, and during the second time interval (of a northward IMF), the observed values of B _sh/B _sw are close to the model curve corresponding to Q _sw=40^o.

Thus, one can see that the behavior of B _sh/B _sw on the day under consideration seems to confirm the model by Pudovkin et al. [1995] and shows the increase of the magnetic barrier intensity with a southward turn of the IMF.

Two more magnetosheath crossings analyzed by Pudovkin et al. [2000b] also demonstrate the existence of a distinct magnetic barrier in the case of a southward IMF.

Thus, experimental data convincingly show that a magnetic barrier, that is, a region of enhanced magnetic field intensity caused by the field line piling against the magnetopause, exists for both northward and southward IMF. What concerns the intensity of the barrier in dependence on the IMF orientation, experimental data presented in Figure 9 show that it increases with the IMF turning southward. Concerning the results by Phan et al. [1994], it is worth noting once more that they considered only the variation of the magnetic field intensity and plasma density in a rather thin (about 2500 km thick) layer just in front of the magnetopause, that is, in the transition layer between the magnetosheath and magnetosphere. And, in our opinion, the data presented in that paper essentially suggest that in the case of a southward IMF, the magnetopause contains a strong, slow shock that transfers to an expansion fan in the case of a northward IMF.

5. Conclusions

We have considered a few problems of magnetosheath physics. Judging by the numerous papers published in recent years, great attention is currently focused on investigations of a possible influence of the anisotropy of plasma temperature on the macro- and microphysical processes developing in the Earth's magnetosheath and in regions of the shocked solar wind. The results of most of the published models show that the temperature anisotropy really influences magnetosheath parameters, such as sheath thickness and the B(x) and n(x) profiles. However, this influence is rather moderate and only slightly changes the characteristics of solar wind flow around the magnetosphere.

This rather unexpected result may be associated with a relatively low level of plasma anisotropy observed in the magnetosheath. This, in turn, suggests the existence of an intensive pitch-angle diffusion of the magnetosheath protons.

And indeed, the temperature anisotropy stimulates the development of various kinetic processes in the magnetosheath plasma resulting in the appearance of a rather intensive plasma turbulence. Both the theoretical and experimental data presented in papers by Gary, Hill, Phan, Paschmann, Denton, Fuselier, Anderson, Hubert, and others allowed them to reveal the wave modes responsible for that turbulence, to identify them mainly with the ion-cyclotron and mirror waves, and to estimate the threshold of the development of the ion-cyclotron and mirror wave instabilities.

However, the linear theory of the plasma turbulence used in those papers has not allowed the authors to calculate the intensity of the developing waves and predict the rate of the proton pitch-angle diffusion. In this vein, there may be some interest in estimates of the characteristic time of the temperature anisotropy relaxation ( t ) obtained from analysis of the experimental data presented above (Figure 5). According to those data, three sub-regions characterized by different intensities of the plasma turbulence may be distinguished within the magnetosheath. The first subregion is a thin layer ( Dx =0.2-0.3 R_E ) adjacent to the bow shock and characterized by a rather intensive (though rapidly decaying with distance) wave turbulence that is probably of the ion-cyclotron mode. The second region occupies the largest part of the magnetosheath and is distinguished by a gradual increase of t to approximately 50 s in the midst of the magnetosheath and a subsequent decrease of t toward the magnetopause to about 20 s; the predominant waves there seem to be mirror-waves. And the third region is the innermost magnetosheath layer adjacent to the magnetopause. The predominant waves there seem again to be the ion-cyclotron modes, and the value of t is about 20 s.

However, these results are obtained from the analysis of greatly smoothed data and do not allow investigation of the dependence of t on the parameters of the solar wind and on the value of the magnetic field and plasma parameters within the magnetosheath. Correspondingly, the problem of wave turbulence and proton pitch-angle diffusion within the magnetosheath requires extensive theoretical and experimental studies.

The problem of the existence or non-existence of the magnetic barrier in dependence on the IMF orientation seems to be somewhat fictitious. The matter is that Phan et al. [1994] have introduced, in essence, a new definition of the magnetic barrier, and it is not surprising that the regularities of the formation and existence of that newly defined structure differ from those peculiar to the barrier detected according to the previous notion. And, taking into account this difference in terminology, the results by Phan et al. [1994] do not contradict the data by Pudovkin et al. [1995]. Indeed, the data by Phan et al. [1994] concern a rather thin region in front of or within the magnetopause and describe the manner in which the magnetosheath magnetic field and plasma density transfer to the magnetospheric one. In the terminology by Pudovkin et al. [1995], this is rather a problem of the formation of a slow shock or an expansion fan within the magnetopause. Contrary to this, in the papers by Pudovkin et al. [1982, 1995], the B(x) and n(x) profiles across the entire magnetosheath are investigated, and a general increase of the magnetic field intensity toward the magnetopause does not contradict the Phan et al. [1994] data, either. The question is how the rate of B(x) increase depends on the IMF orientation. However, this question has not been investigated by Phan et al.

Experimental data presented by Pudovkin et al. [1995] confirm their model. At the same time, and this has to be emphasized once more, this model is based on strong supposition of the topology of the magnetosheath plasma flow, and this supposition needs both the theoretical and experimental confirmation or disproof.

Acknowledgments

References

Alksne, A. J., The steady-state magnetic field in the transition region between the magnetosphere and the bow shock, Planet. Space Sci., 15, 239, 1967.

Anderson, B. J., and S. A. Fuselier, Magnetic pulsations from 0.1 to 4.0 Hz and associated properties in the Earth's subsolar magnetosheath and plasma depletion layer, J. Geophys. Res., 98, 1461, 1993.

Anderson, B. J., S. A. Fuselier, S. P. Gary, and R. E. Denton, Magnetic spectral signatures in the Earth's magnetosheath and plasma depletion layer, J. Geophys. Res., 99, 5877, 1994.

Anderson, B. J., S. A. Fuselier, and D. Murr, Electromagnetic ion cyclotron waves observed in the plasma depletion layer, Geophys. Res. Lett., 18, 1955, 1991.

Aubry, M. P., C. T. Russell, and M. G. Kivelson, Inward motion of the magnetopause before a substorm, J. Geophys. Res., 75, 7018, 1970.

Chew, G. F., M. L. Goldberger, and F. E. Low, The Boltzmann equation and the one-fluid hydromagnetic equations in the absence of particle collisions, Proc. R. Soc. London A, 236, 112, 1956.

Denton, R. E., and J. G. Lyon, Effect of pressure anisotropy on the structure of a two-dimensional magnetosheath, J. Geophys. Res., 105, 7545, 2000.

Denton, R. E., B. J. Anderson, S. P. Gary, and S. A. Fuselier, Bounded anisotropy fluid model for ion temperature, J. Geophys. Res., 99, 11,225, 1994.

Denton, R. E., X. Li, and T.-D. Phan, Bounded anisotropy fluid model for ion temperature evolution applied to AMPTE/IRM magnetosheath data, J. Geophys. Res., 100, 14,925, 1995.

Erkaev, N. V., Solar wind flow around the Earth's magnetosphere (in Russian), Nauka, Moscow, 1989.

Erkaev, N. V., C. J. Farrugia, and H. K. Biernat, Three-dimensional, one-fluid, ideal MHD model of the magnetosheath flow with anisotropic pressure, J. Geophys. Res., 104, 6877, 1999.

Fairfield, D. H., Averaged and unusual locations of the Earth's magnetopause and bow shock, J. Geophys. Res., 76, 6700, 1971.

Feldman, W. C., in Magnetospheric phenomena in Astrophysics, AIP Conference Proc. N 144, edited by R. J. Epstein, p. 145, New York, 1986.

Gary, S. P., The mirror and ion cyclotron anisotropy instabilities, J. Geophys. Res., 97, 8519, 1992.

Gary, S. P., Theory of Space Plasma Microinstabilities, Cambridge Univ. Press, New York, 1993.

Gary, S. P., and D. Winske, Simulation of ion cyclotron anisotropy instabilities in the terrestrial magnetosheath, J. Geophys. Res., 98, 9171, 1993.

Gary, S. P., S. A. Fuselier, and B. J. Anderson, Ion anisotropy instabilities in the magnetosheath, J. Geophys. Res., 98, 1481, 1993a.

Gary, S. P., M. E. McKean, and D. Winske, Ion cyclotron anisotropy instabilities in the magnetosheath: Theory and simulations, J. Geophys. Res., 98, 3963, 1993b.

Gary, S. P., M. E. McKean, D. Winske, B. J. Anderson, and S. A. Fuselier, The proton cyclotron instability and the anisotropy/ b inverse correlation, J. Geophys. Res., 99, 5903, 1994a.

Gary, S. P., P. D. Convery, R. E. Denton, S. A. Fuselier, and B. J. Anderson, Proton and helium cyclotron anisotropy instability threshold in the magnetosheath, J. Geophys. Res., 99, 5915, 1994b.

Hau, L.-N., T.-D. Phan, B. U. Ö. Sonnerup, and G. Paschmann, Double-polytropic closure in the magnetosheath, Geophys. Res. Lett., 20, 2255, 1993.

Hill, P., G. Paschmann, R. A. Treumann, W. Baumjohann, N. Sckopke, and H. Lühr, Plasma and magnetic field behavior across the magnetosheath near local noon, J. Geophys. Res., 100, 9575, 1995.

Hubert, D., Nature and origin of wave modes in the dayside Earth magnetosheath, Adv. Space Res., 14, 55, 1994.

Hubert, D., C. Lancombe, C. C. Harvey, M. Moncuquet, C. T. Russell, and M. F. Thomsen, Nature, properties, and origin of low-frequency waves from an oblique shock to the inner magnetosheath, J. Geophys. Res., 103, 26,783, 1998.

Kovner, M. S., and Ya. I. Feldstein, On solar wind interaction with the Earth's magnetosphere, Planet. Space Sci., 21, 1191, 1973.

Parker, E. N., Comments on the reconnection rate of magnetic fields, J. Plasma Phys., 9, 49, 1973.

Phan, T.-D., G. Paschmann, and W. Baumjohann, The magnetosheath region adjacent to the dayside magnetopause: AMPTE/IRM observations, J. Geophys. Res., 99, 121, 1994.

Phan, T.-D., et al., The subsolar magnetosheath and magnetopause for high solar wind ram pressure, Geophys. Res. Lett., 23, 1279, 1996a.

Phan, T.-D., G. Paschmann, and B. U. Ö. Sonnerup, Low-latitude dayside magnetopause and boundary layer for high magnetic shear: 2. Occurrence of magnetic reconnection, J. Geophys. Res., 101, 7817, 1996b.

Pudovkin, M. I., and V. S. Semenov, Peculiarities of the MHD flow by the magnetopause and generation of the electric field in the magnetosphere, Ann. Geophys., 33, 423, 1977.

Pudovkin, M. I., and V. A. Lebedeva, Solar wind parameters in the magnetosheath in the model with a magnetic barrier, Geomagn. Aeron. (in Russian), 27, 22, 1987.

Pudovkin, M. I., and A. A. Samsonov, Anisotropic model for the dayside magnetosheath, in Problems of Geospace 2 (Proc. 2nd International Workshop, St. Petersburg, Russia, June 29-July 3, 1998), edited by V. S. Semenov, H. K. Biernat, M. V. Kubyshkina, C. J. Farrugia, and S. Mühlbachler, pp. 95-99, Verlag der Österreichischen Akademie der Wissenschaften, 1999.

Pudovkin, M. I., B. P. Besser, V. V. Lebedeva, S. A. Zaitseva, and C.-V. Meister, Magnetosheath model in the Chew-Goldberger-Low approximation, Phys. Plasmas, 6, 2887, 1999.

Pudovkin, M. I., B. P. Besser, and S. A. Zaitseva, Magnetopause stand-off distance in dependence on the magnetosheath and solar wind parameters, Ann. Geophys., 16, 388, 1998.

Pudovkin, M. I., B. P. Besser, S. A. Zaitseva, V. V. Lebedeva, and C.-V. Meister, Magnetic barrier in case of a southward IMF, J. Atmos. Sol.-Terr. Phys., in press, 2000b.

Pudovkin, M. I., M. F. Heyn, and V. V. Lebedeva, Magnetosheath's parameters in dependence on the direction of the solar wind magnetic field, J. Geophys. Res., 87, 8131, 1982.

Pudovkin, M. I., T. V. Kuznetsova, and S. A. Zaitseva, Location of the dayside magnetopause in dependence on the IMF direction, in Magnetospheric Researches (in Russian), No. 3, pp. 14-24, 1984.

Pudovkin, M. I., S. A. Zaitseva, and B. P. Besser, Magnetosheath magnetic barrier parameters in dependence on the solar wind magnetic field orientation, Ann. Geophys., 13, 828, 1995.

Pudovkin, M. I., S. A. Zaitseva, and C.-V. Meister, Proton pitch-angle diffusion rate and polytropic index values in the magnetosheath: Model and experiment, Int. J. Geomagn. Aeron., 2, 93, 2000a.

Samsonov, A. A., and M. I. Pudovkin, Ideal anisotropic plasma flow round a sphere in the CGL-approach, Geomagn. Aeron. (in Russian), 38, 50, 1998.

Samsonov, A. A., and M. I. Pudovkin, Application of the bounded anisotropy model for the dayside magnetosheath, J. Geophys. Res., 105, 12,859, 2000.

Sckopke, N., G. Paschmann, A. L. Brinca, C. W. Carlson, and H. Luehr, Ion thermalization in quasi-perpendicular shocks involving reflected ions, J. Geophys. Res., 95, 6337, 1990.

Spreiter, J. R., A. L. Summers, and A. Y. Alksne, Hydromagnetic flow around the magnetosphere, Planet. Space Sci., 14, 223, 1966.

Tsyganenko, N. A., and D. G. Sibeck, Concerning flux erosion from the dayside magnetosphere, J. Geophys. Res., 99, 13,425, 1994.

Yeh, T., Day-side reconnection between a dipolar geomagnetic field and a uniform interplanetary field, J. Geophys. Res., 81, 2140, 1976.

Zwan, B. J., and R. A. Wolf, Depletion of solar wind plasma near a planetary boundary, J. Geophys. Res., 81, 1636, 1976.