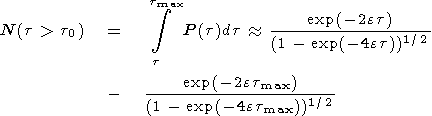International Journal of Geomagnetism and Aeronomy
Vol 2, No. 2, August 2000
Peculiar features of burst series
of long-period irregular
ipcl-type geomagnetic pulsations in the vicinity
of the dayside cusp
N. A. Kurazhkovskaya and B. I. Klain
Geophysical Observatory Borok, Institute of Physics of the Earth,
Borok, Yaroslavskaya Region, Russia
Contents
Abstract
Using the Mirny Observatory data
(F = -77o magnetic latitude),
we
revealed and studied morphological characteristics of series of
ipcl-type bursts. This paper shows that the ipcl burst series are
observed predominantly during moderate geomagnetic activity
(Kp 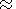 2-3) in the 0800-1600 magnetic
local time
interval corresponding to the Mirny
Observatory passage across the region of the dayside cusp
projection. Analysis of the ipcl burst length
(t) distribution and dependence of
t on the burst-filling frequency
shows that the ipcl burst series observed are the
intermittent process. We assume that the ipcl burst series are
caused by stochastic of current structures in the polar cusp.
2-3) in the 0800-1600 magnetic
local time
interval corresponding to the Mirny
Observatory passage across the region of the dayside cusp
projection. Analysis of the ipcl burst length
(t) distribution and dependence of
t on the burst-filling frequency
shows that the ipcl burst series observed are the
intermittent process. We assume that the ipcl burst series are
caused by stochastic of current structures in the polar cusp.
1. Introduction
Studies of the long-period irregular geomagnetic pulsations of the
ipcl type (irregular pulsations, continuous, long) observed in the
regions of the polar cap and dayside cusp had already begun in the
1970s
[Bol'shakova et al., 1974;
Troitskaya et al., 1973].
During subsequent decades, many publications appeared in
Russia and abroad whose goal was to study the ipcl
morphology and to analyze their possible excitation mechanisms.
However, there is still no consensus regarding the
nature of these pulsations and physical conditions for their
generation.
Bol'shakova and Troitskaya [1982]
drew attention to the fact, that
during changes of the interplanetary magnetic field (IMF) from
southward to northward there may occur singular intense ipcl
bursts. Processing multiyear observations of the magnetic field in
the Mirny Observatory ( -77o magnetic latitude (MLAT)),
we discovered that observed
under moderate geomagnetic activity are not singular bursts of the
ipcl pulsations but series of bursts which demonstrate
morphological features different from the characteristics of the usual
ipcl regime and in no way are related to orientation changes of
IMF. What is more, not only the bursts within a particular series but
also
the occurrence of the series themselves have no relation to the above
changes. The morphological features of the series of ipcl bursts
detected in our studies differ principally by their structure and
dynamics from the singular bursts considered by
Bol'shakova and Troitskaya [1982].
The goal of this paper is to study the main morphological
characteristics of the ipcl burst series and their relationship to
geomagnetic disturbance and solar wind parameters and to
reveal physical conditions and mechanisms for ipcl burst
formation.
2. Experimental Data
We used the Mirny Observatory
(F = -77o MLAT) magnetograms
with
90 mm h
-1 scanning within the 2.1- to 5.5-mHz
frequency band and the
J. H. King catalog data
[King, 1986].
For the period from 1981 to 1986
we selected about 50 ipcl burst series. We chose the events whose
H component burst amplitudes exceeded the background by 6-10 times
and were, on average, 20-40 nT. Each series lasted for 2-8
hours. Each series involved 3-8 bursts. The average length of an
individual burst was 30-35 min. The burst repetition period was
20-25 min. The average burst-filling frequency was 4.1-5.5 mHz.
As the data analysis showed, all events under consideration were
observed at moderate geomagnetic activity
(Kp 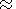 2-3,
Bx > 0,
By < 0,
Bz > 0 ) near noon (0800-1600
magnetic local time (MLT)).
It follows from the statistical analysis of the dayside cusp
dynamics under various levels of geomagnetic activity, orientation,
and magnitude of IMF that the statistical mean position of the cusp
in the southern hemisphere corresponds to geomagnetic latitudes of
72o-80
o [Candidi et al., 1989;
Newell et al., 1989].
2-3,
Bx > 0,
By < 0,
Bz > 0 ) near noon (0800-1600
magnetic local time (MLT)).
It follows from the statistical analysis of the dayside cusp
dynamics under various levels of geomagnetic activity, orientation,
and magnitude of IMF that the statistical mean position of the cusp
in the southern hemisphere corresponds to geomagnetic latitudes of
72o-80
o [Candidi et al., 1989;
Newell et al., 1989].
It follows from the aforesaid and the geographic location of
the Mirny Observatory that around noon under
Kp 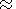 2-3 this
observatory is located under the region of the dayside cusp
projection. Presented below are the results of the studies of the
principal characteristics of the most representative ipcl bursts in
the
H component of the magnetic field registered in the region of
the polar cusp.
2-3 this
observatory is located under the region of the dayside cusp
projection. Presented below are the results of the studies of the
principal characteristics of the most representative ipcl bursts in
the
H component of the magnetic field registered in the region of
the polar cusp.
3. Results and Discussion
 Figure 1 shows a typical example of the ipcl burst series in
the
H component revealed from the Mirny Observatory
(F = -77o) data obtained April
1, 1986, at 0512-1030 UT. As Figure 1
shows, the bursts are quasi-periodic structures arising against the
noise background.
It is characteristic that no ipcl burst structures are observed
neither under magnetic disturbance increase ( Kp > 3 ) nor under
conditions of quiet magnetosphere ( Kp < 2 ).
Figure 1 shows a typical example of the ipcl burst series in
the
H component revealed from the Mirny Observatory
(F = -77o) data obtained April
1, 1986, at 0512-1030 UT. As Figure 1
shows, the bursts are quasi-periodic structures arising against the
noise background.
It is characteristic that no ipcl burst structures are observed
neither under magnetic disturbance increase ( Kp > 3 ) nor under
conditions of quiet magnetosphere ( Kp < 2 ).
The diurnal ipcl burst distribution with the local geomagnetic time
exhibits two maxima at 0900 and 1300 MLT. Earlier and later the
probability of the burst occurrence decreases by an order of
magnitude. The two maxima in the distribution of the ipcl burst
generation probability with local geomagnetic time are,
apparently, connected with the Mirny Observatory crossing the
dayside polar cusp boundaries and with the processes in the
near-boundary segments of the cusp. As
Zanetty et al. [1981]
reported, the cusp boundaries are characterized by a pronounced
inhomogeneity in the particle density and by intense
field-aligned
currents which cause the wave turbulence in the cusp.
Now consider the interplanetary conditions for generation of the
ipcl burst series. Using the hourly data from the catalog of
King [1986],
we constructed the distributions of the solar wind velocity
V, plasma density
n, field modulus
B, dynamic solar wind pressure
rV2, IMF components
Bx,
By, and
Bz, and
latitude
q and longitude
j of the IMF vector in the
solar-ecliptic frame of reference.
The histograms obtained showed that as a rule, series of ipcl bursts
are generated under
V 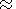 400-500 km s
-1,
n
400-500 km s
-1,
n 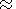 5-10 cm
-3,
B
5-10 cm
-3,
B 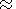 6-8 nT, and
rV2
6-8 nT, and
rV2 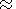 (3-4)
(3-4)
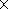 10-8 dyn cm
-2.
Analysis of the
Bx,
By, and
Bz IMF components shows
that in more than 60% of the cases the ipcl bursts are observed in the
positive direction of the radial component, the negative direction of
the azimuthal component, and the northward direction of the vertical
component of the IMF
(Bx > 0,
By < 0,
Bz > 0). Estimates of
angles characterizing the IMF orientation show that the ipcl burst
series are observed predominantly within the latitude range
q
10-8 dyn cm
-2.
Analysis of the
Bx,
By, and
Bz IMF components shows
that in more than 60% of the cases the ipcl bursts are observed in the
positive direction of the radial component, the negative direction of
the azimuthal component, and the northward direction of the vertical
component of the IMF
(Bx > 0,
By < 0,
Bz > 0). Estimates of
angles characterizing the IMF orientation show that the ipcl burst
series are observed predominantly within the latitude range
q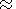 0o-30o
and the longitude range
j
0o-30o
and the longitude range
j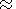 310o-320o,
i.e., when the IMF is directed sunward in the
ecliptic plane. The combination of empiric distributions of
interplanetary medium parameters demonstrates the moderateness of
the magnetospheric disturbance, which serves as a background for the
ipcl burst series. Since ipcl bursts are observed at the dayside
cusp latitude predominantly at
Kp
310o-320o,
i.e., when the IMF is directed sunward in the
ecliptic plane. The combination of empiric distributions of
interplanetary medium parameters demonstrates the moderateness of
the magnetospheric disturbance, which serves as a background for the
ipcl burst series. Since ipcl bursts are observed at the dayside
cusp latitude predominantly at
Kp 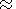 2-3,
Bz > 0,
By < 0,
and
Bx > 0, the generation of the ipcl bursts is not, apparently,
related to the IMF southward rotation, and thus it is not related
to a development of the impulse reconnection at the dayside
magnetopause.
Parker [1979]
and
Vainshtein [1985]
showed that the
necessary conditions for the latter are high magnetic activity,
southward direction of the IMF vertical component
(Bz < 0),
By > 0, and
Bx < 0.
2-3,
Bz > 0,
By < 0,
and
Bx > 0, the generation of the ipcl bursts is not, apparently,
related to the IMF southward rotation, and thus it is not related
to a development of the impulse reconnection at the dayside
magnetopause.
Parker [1979]
and
Vainshtein [1985]
showed that the
necessary conditions for the latter are high magnetic activity,
southward direction of the IMF vertical component
(Bz < 0),
By > 0, and
Bx < 0.
As a principal characteristic of the bursts, their duration
t was chosen which is determined as follows: An
envelope of
the burst amplitude was found for each burst series. The duration
of each particular burst was evaluated at the 0.7 level of the
maximum amplitude of the burst.
 Figure 2a demonstrates a histogram of the ipcl burst
lengths. We can see that
t ranges from 10 to 100 min. A specific
feature of this distribution is a long tail at large
t. The
distribution of the burst lengths has a maximum at low
t and
decreases algebraically at large
t. In other words, the
distribution function of
t is rather distinctive, which gives us
an opportunity to identify the ipcl burst series observed with
modes given by the theoretical concepts.
Figure 2a demonstrates a histogram of the ipcl burst
lengths. We can see that
t ranges from 10 to 100 min. A specific
feature of this distribution is a long tail at large
t. The
distribution of the burst lengths has a maximum at low
t and
decreases algebraically at large
t. In other words, the
distribution function of
t is rather distinctive, which gives us
an opportunity to identify the ipcl burst series observed with
modes given by the theoretical concepts.
Figure 1 shows that the ipcl burst series are signals in which
in a
random way alternate weakly disturbed oscillations and periodical
bursts. Such behavior of the signal is typical for the transition
to chaos through alternating. Transitions from the chaotic
regime to the quasi-periodic regime as well as from chaotic regime
(1) to chaotic regime (2) may be observed. The transition to chaos
through alternating leads to formation, in the phase space, of the
system considered to be of a chaotic attractor
[Grebogi et al., 1987].
It
is known
[e.g., Berzhe et al., 1991]
that there exist two types of
alternating, each having its own peculiarities.
The classification of transitions to chaos through alternating
in three burst types (I, II, and III) is based on three types of linear
instabilities of periodical trajectories
[Berzhe et al., 1991].
Each
type of alternating corresponds to quite definite distribution of
the burst duration near the alternating threshold. Evidently, the
ipcl burst series registered at Mirny may be considered as an
intermediate regime of transition from one chaotic regime to
another chaotic regime, the transition occurring though
alternating. This means that the signal observed is interrupted
by
alternating bursts (see Figure 1). Under magnetospheric condition
changes the number of bursts increases until the regime becomes
completely chaotic (we see this under
Kp > 3 ). According to the
visual picture of the ipcl pulsation burst series and the typical
distribution function of the burst duration (see Figures 1 and 2a)
the ipcl burst series have a property of transition to chaos
through the alternating of type III. Actually, the burst
duration distribution (see Figure 2a) may be identified with the
duration distribution of usual periodical oscillations near the
alternating threshold typical to alternating of type III
according to the classification of
Berzhe et al. [1991].
Comparison of the experimental data with theoretical calculations
confirms this assumption. According to
Berzhe et al. [1991]
the
burst number normalized to the total amount of cases
N with the
duration
t t0
should meet the condition
t0
should meet the condition
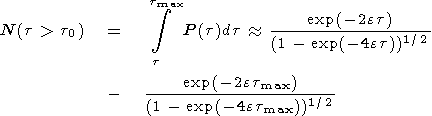 | (1) |
where
P(t) is the probability of burst duration
observation,
e is a governing parameter, and
t0 is the shortest burst
duration.
 The function
N is entirely governed by the
e value.
Figure 2b
shows the comparison between the solutions of (1) and
experimental data. We obtained the experimental curve (circles) from
the histogram in Figure 2a by summing up the likelihoods of ipcl
burst length observations. The theoretical curve (solid line)
was obtained from (1). The relation (1) fits best the observations
at
e = 0.014. The standard deviation is
s
The function
N is entirely governed by the
e value.
Figure 2b
shows the comparison between the solutions of (1) and
experimental data. We obtained the experimental curve (circles) from
the histogram in Figure 2a by summing up the likelihoods of ipcl
burst length observations. The theoretical curve (solid line)
was obtained from (1). The relation (1) fits best the observations
at
e = 0.014. The standard deviation is
s 0.08.
Therefore the experimental distribution of the ipcl burst lengths
is in a rather good agreement with the distribution inherent to the
type III intermittence.
It is worth noting that in the case of other alternating types (I, II)
the burst duration distribution is ruled by other laws
[Berzhe et al., 1991].
0.08.
Therefore the experimental distribution of the ipcl burst lengths
is in a rather good agreement with the distribution inherent to the
type III intermittence.
It is worth noting that in the case of other alternating types (I, II)
the burst duration distribution is ruled by other laws
[Berzhe et al., 1991].
 On the other hand, according to
Grebogi et al. [1987],
in the
vicinity of the critical transitions, the following relation must
be true for the intermittence modes:
On the other hand, according to
Grebogi et al. [1987],
in the
vicinity of the critical transitions, the following relation must
be true for the intermittence modes:
 | (2) |
where
p is any parameter which characterizes the system,
pc is the
critical value of the parameter under which the system transits
from one regime to another, and
g is the critical power index.
Herein
p - pc  e, where
e is the governing
parameter from (1). In our case the role of parameter
p may be
played by the frequency of the filling of bursts ( f
).
Analyzing the
relation between the burst duration and the frequency of the filling of
bursts, we found a relation between
t and
f similar to (2).
Figure 3
shows the average ipcl burst length versus the average
burst-filling frequency. Each circle in Figure 3 corresponds to an
individual ipcl burst series. The analysis was performed for
ipcl
burst series having the average burst filling frequency of 2.1-4.2 mHz.
When
f > 4.2 mHz, the shape of the
t (f) dependence
changes. Figure 3
shows that in this frequency band,
t decreases
inversely to
f. The function (2) fits the dependence
t (f) adequately.
The solid line shows the theoretical dependence of
t on
f. The value
of the critical power index
g was evaluated by the least
squares method and was found equal to about 0.5. This means that the
mean burst duration diverges as
e-0.5
e, where
e is the governing
parameter from (1). In our case the role of parameter
p may be
played by the frequency of the filling of bursts ( f
).
Analyzing the
relation between the burst duration and the frequency of the filling of
bursts, we found a relation between
t and
f similar to (2).
Figure 3
shows the average ipcl burst length versus the average
burst-filling frequency. Each circle in Figure 3 corresponds to an
individual ipcl burst series. The analysis was performed for
ipcl
burst series having the average burst filling frequency of 2.1-4.2 mHz.
When
f > 4.2 mHz, the shape of the
t (f) dependence
changes. Figure 3
shows that in this frequency band,
t decreases
inversely to
f. The function (2) fits the dependence
t (f) adequately.
The solid line shows the theoretical dependence of
t on
f. The value
of the critical power index
g was evaluated by the least
squares method and was found equal to about 0.5. This means that the
mean burst duration diverges as
e-0.5 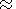 (f - fc)-0.5 when approaching the alternating
threshold.
(f - fc)-0.5 when approaching the alternating
threshold.
According to theoretical concepts the critical power index for the
type III intermittent processes is expected to be
g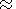 0.66.
We can see that
g found from experimental data for the
ipcl burst series agrees with the theoretical critical exponent
[Berzhe et al., 1991].
0.66.
We can see that
g found from experimental data for the
ipcl burst series agrees with the theoretical critical exponent
[Berzhe et al., 1991].
Thus the qualitative behavior of the functions
N = N(t >
t0)
and
t = t (f)
leads to the conclusion that ipcl pulsation
burst series are an alternating process. Such processes have
universal properties, are detected in numerous experiments, and in
nature are related to the transition to turbulence. Since the
ipcl burst series, registered at the cusp latitudes, demonstrate
characteristic properties typical for a transition to chaos
through alternating, probably ground observations of such series
are a manifestation of the turbulence development dynamics in the
cusp.
 We studied further the relation between the average duration of the
ipcl pulsation bursts and the parameters of the solar wind and
interplanetary magnetic field such as
n,
V,
rV2,
B,
Bx,
By,
and
Bz components. The burst duration
t was found to depend on
the IMF modulus (Figure 4). The dependence of
t on
B is based on
the ipcl burst series for which there were data on IMF in the
King [1986]
catalog. Each point in Figure 4 corresponds to a
particular burst series. The IMF modulus was averaged for several
hours of burst series observations. Within each ipcl burst series
the IMF modulus changed only slightly, so the standard deviation
did not exceed 10% of the mean values of
B.
We studied further the relation between the average duration of the
ipcl pulsation bursts and the parameters of the solar wind and
interplanetary magnetic field such as
n,
V,
rV2,
B,
Bx,
By,
and
Bz components. The burst duration
t was found to depend on
the IMF modulus (Figure 4). The dependence of
t on
B is based on
the ipcl burst series for which there were data on IMF in the
King [1986]
catalog. Each point in Figure 4 corresponds to a
particular burst series. The IMF modulus was averaged for several
hours of burst series observations. Within each ipcl burst series
the IMF modulus changed only slightly, so the standard deviation
did not exceed 10% of the mean values of
B.
Figure 4 shows that when
B increases, the burst length decreases by
~3 times. When
B reaches a certain critical value ( B = 7 nT),
the character of
t (B) dependence changes. When the field
modulus increases further,
t also increases, and at
B > 9 nT, the
ipcl bursts are not observed.
Thus the
t dependence on
B obtained experimentally leads to an
assumption that the destruction of the burst structure begins at
B> 7 nT and only a ipcl homogeneous background exists under further
increase of the IMF modulus. In other words, when
B reaches its
critical value, there occurs a destruction of the attractor of the
ipcl pulsation vibrational process (a crisis according to the
terminology of
Grebogi et al. [1987]).
It should be noted that we
detected no dependence of the burst mean duration on other
parameters of the solar wind and IMF.
There are at least two approaches to the problem of excitation of
long-period irregular pulsations of the ipcl type. For example,
based on the analysis of the homogeneous regime of the ipcl
irregular pulsation generation (the regime appears under a change
of the IMF vertical component from the northward to southward),
Bol'shakova and Troitskaya [1982]
suggested that the pulse
reconnection is a cause of ipcl.
A different approach was considered
by
Friis-Christensen et al. [1988]
and
McHenry et al. [1990].
Using
the observations of ipcl pulsations at the Greenland chain of
observatories, they showed that ipcl excitation is accompanied by
traveling vortices of convection in the ionosphere. It should be
noted that occurrence of both the pulse reconnection and
the ionospheric vortices is related to formation of the field-aligned
current tubes, their behavior depending significantly on the
character of the solar wind flowing around the magnetosphere.
As the analysis of the ipcl burst series characteristics and of the
interplanetary medium conditions for generation of the ipcl bursts
shows that the generation of the ipcl quasi-periodic bursts at the
dayside cusp latitude does not agree with the impulse reconnection
model. We obtained a number of experimental facts demonstrating
that the ipcl burst series are the intermittent processes.
Moreover, under
Bz > 0,
By < 0 ipcl pulsations burst series are
observed in the cusp region of the southern hemisphere
magnetosphere. It is widely known that under these conditions there
exists an intense system of field-aligned currents in the polar
cusp. Thus the fact that the ipcl generation is related to the
large-scale field-aligned currents is a common feature for all the
ipcl regimes observed.
Naturally, a question arises
whether it is possible to construct
directly a model with a finite number of degrees of freedom which
can simulate adequately the qualitative aspects of the described
turbulence structuring derived from the ipcl pulsation
observations.
According to
Volkov and Zubarev [1995],
a generation of large-scale
vortex-like structures, which are described by the model analogous
to the Lorentz model, is possible in the current-containing
plasma-like medium. The processes in which a transfer to chaos
through alternating are related to such models
[Berzhe et al., 1991].
Taking into account the results of this paper and those of
Volkov and Zubarev [1995],
one is able to understand at a
qualitative level the mechanism of ipcl burst generation.
Most
likely, the ipcl temporal structures are associated with the polar
cusp vortex current structures whose randomization causes the observed
effects.
4. Conclusions
The main results of this paper are as follows:
1. Using the observations at the Mirny Station, ipcl pulsation
burst series, which have some specific properties not typical for
the usual ipcl regime, are detected and studied.
2. It is demonstrated that the ipcl burst series are not related to
the IMF reversal and are observed at moderate geomagnetic activity
within the 0008-1600 MLT interval which corresponds to the passage
over Mirny of the dayside cusp projection.
3. We found that the burst length distribution agrees well with
the theoretical distribution for the systems in which the
transition to chaos goes on by way of the type III intermittence.
4. We revealed the existence of a critical value of the IMF
intensity modulus at which the burst structures are destroyed.
5. We assumed that the ipcl burst series observed at the dayside
polar cusp latitude are induced by stochastic processes
of large-scale
current vortex structures.
Acknowledgment
This work was supported by the Russian Foundation
for Basic Research (project 94-05-17564).
References
Berzhe, P., I. Pomo, and K. Vidal', Order in Chaos (in Russian),
367 pp., Mir,
Moscow, 1991.
Bol'shakova, O. V., and V. A. Troitskaya, Impulse reconnection as a
possible source of ipcl pulsations, Geomagn. Aeron. (in Russian), 22 (5),
877,
1982.
Bol'shakova, O. V., I. N. Men'shutina, and M. I. Pudovkin,
Relationship of the high-latitude dayside geomagnetic field
pulsations with periods of 5-10 min to the solar wind parameters,
Antarktika (in Russian), 13, 5, 1974.
Candidi, M., et al., Evidence of influence of the interplanetary magnetic
field azimuthal component on polar cusp configuration,
J. Geophys. Res., 94 (A10),
13,585, 1989.
Friis-Christensen, E., et al., Irregular magnetic pulsations in the
polar cleft caused by travelling ionospheric convection vortices,
Adv. Space Res., 8 (9-10), 9311, 1988.
Grebogi, C., et al., Critical exponents for crisis-induced
intermittency, Phys. Rev. A, 36 (11),
36, 1987.
King, J. H., Interplanetary Medium Data Book, Suppl. 3, 1977-1985,
World Data Cent. A for Rockets and Satellites, Greenbelt, Md., 1986.
McHenry, M. A., C. R. Clauer, and E. Friis-Christensen,
Relationship of solar wind parameters to continuous, dayside
high-latitude traveling ionospheric convection vortices,
J. Geophys. Res., 95 (A9),
15,007, 1990.
Newell, P. T., et al., Some low-altitude cusp dependencies on the
interplanetary field,
J. Geophys. Res., 94 (A7),
8921, 1989.
Parker, E. N., Cosmic Magnetic Fields, Clarendon, Oxford,
England, 1979.
Sandholt, P. E., et al., Large- and small-scale dynamics of the
polar cusp, J. Geophys. Res., 90 (5),
4407, 1985.
Troitskaya, V. A., O. V. Bol'shakova, and V. B. Hessler,
Irregular geomagnetic pulsations in the polar cap,
Rep. Assem. IAGA,
Int. Assoc. of Geomagn. and Aeron., Rockville, Md.,
1973.
Vainshtein, C. I., Magnetic Hydrodynamics of Space Plasma and Current Layers
(in Russian), 192 pp., Nauka, Moscow, 1985.
Volkov, N. B., and N. M. Zubarev, A model for initial phase of a
laminar-turbulent transition within the current-bearing plasma-type
medium, Zh. Eksp. Teor. Fiz. (in Russian), 107 (6), 1868, 1995.
Zanetty, L. J., et al., Magnetic-field-aligned electron
distribution in the dayside cusp, J. Geophys. Res., 86,
8957, 1981.
Load files for printing and local use.
This document was generated
by TeXWeb
(Win32, v.2.0) on August 3, 2000.
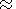 2-3,
Bx > 0,
By < 0,
Bz > 0 ) near noon (0800-1600
magnetic local time (MLT)).
It follows from the statistical analysis of the dayside cusp
dynamics under various levels of geomagnetic activity, orientation,
and magnitude of IMF that the statistical mean position of the cusp
in the southern hemisphere corresponds to geomagnetic latitudes of
72o-80
o [Candidi et al., 1989;
Newell et al., 1989].
2-3,
Bx > 0,
By < 0,
Bz > 0 ) near noon (0800-1600
magnetic local time (MLT)).
It follows from the statistical analysis of the dayside cusp
dynamics under various levels of geomagnetic activity, orientation,
and magnitude of IMF that the statistical mean position of the cusp
in the southern hemisphere corresponds to geomagnetic latitudes of
72o-80
o [Candidi et al., 1989;
Newell et al., 1989].

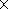 10-8 dyn cm
-2.
Analysis of the
Bx,
By, and
Bz IMF components shows
that in more than 60% of the cases the ipcl bursts are observed in the
positive direction of the radial component, the negative direction of
the azimuthal component, and the northward direction of the vertical
component of the IMF
(Bx > 0,
By < 0,
Bz > 0). Estimates of
angles characterizing the IMF orientation show that the ipcl burst
series are observed predominantly within the latitude range
q
10-8 dyn cm
-2.
Analysis of the
Bx,
By, and
Bz IMF components shows
that in more than 60% of the cases the ipcl bursts are observed in the
positive direction of the radial component, the negative direction of
the azimuthal component, and the northward direction of the vertical
component of the IMF
(Bx > 0,
By < 0,
Bz > 0). Estimates of
angles characterizing the IMF orientation show that the ipcl burst
series are observed predominantly within the latitude range
q
 t0
should meet the condition
t0
should meet the condition