 the current density
j,
the velocity potential
is similar to the magnetic field potential, and current velocity
function
the current density
j,
the velocity potential
is similar to the magnetic field potential, and current velocity
function
 the magnetic flux), the hydrodynamical
results
are automatically transposed to magnetostatics.
the magnetic flux), the hydrodynamical
results
are automatically transposed to magnetostatics.
Yu. A. Romashchenko and P. D. Reshetnikov
Institute of Space Physics and Aeronomy, Yakutsk, Sakha Republic, Russia
For solution of theoretical and experimental problems of magnetospheric physics, one should take a magnetic field model of the Earth's magnetosphere. Currently, there exist very reliable empirical magnetospheric models of which we would like to mention the Tsyganenko models [Sergeev and Tsyganenko, 1980; Tsyganenko, 1990]. The only defect of these models is their multiparameterization that is not always convenient in consideration of some theoretical problems. Therefore we suggest a very simple model of the inner magnetosphere based on a solution of the problem of a closed displaced dipole in a spherical cavity. We solved this problem a long time ago [Krymskiy and Romashchenko, 1975], but we believe that this paper is of some interest, again owing to the new attention given to magnetospheric cusp physics. Moreover, the early paper was published in a peripheral journal and has an error (the integration constant was determined incorrectly).
The problem is to determine the magnetic field of an inclined dipole placed in a sphere with radius a, the sphere center, and dipole not coinciding. The dipole axis may precess with a constant angular velocity W. The magnetic field normal component at the sphere boundary is zero.
For solving of this internal problem of magnetostatics we use
the results of the Veiss theorem for a sphere
[Milne-Thomson, 1964].
Since this theorem is seldom used in the physics of
magnetic phenomena related to magnetospheric process modeling, we
formulate this theorem in full. It is necessary to take into
account that the Veiss theorem was formulated in hydrodynamical
terms, but since the equations of hydrodynamics and nondissipative
electrodynamics (in particular, magnetostatics) coincide
apart from constants
(the velocity v is similar to the
magnetic field B, rot
v  the current density
j,
the velocity potential
is similar to the magnetic field potential, and current velocity
function
the current density
j,
the velocity potential
is similar to the magnetic field potential, and current velocity
function
 the magnetic flux), the hydrodynamical
results
are automatically transposed to magnetostatics.
the magnetic flux), the hydrodynamical
results
are automatically transposed to magnetostatics.
In a boundless space, let there be an irrotational flow of an ideal incompressible liquid with the velocity potential j(r,q,w) in spherical coordinates j(r,q,w), all singular points of this function being placed at a distance from the origin larger than a. If one places a sphere with r = a into the region of this flow, then the velocity potential that causes the normal component of velocity at the surface of the sphere to vanish may be expressed as
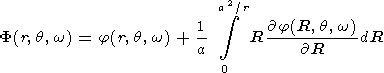 | (1) |
The proof of this theorem was presented by Milne-Thomson [1964], so we do not present it here.
 Use the results of the above mentioned theorem for solution of the
problem on a radial dipole placed outside the sphere.
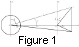
Thus let there be a sphere with
r = a placed into a spherical
coordinate system with the center
at the origin.
At a
distance
f from the sphere center
(f > a) we place a dipole
with the magnetic moment
M (Figure 1).
Use the results of the above mentioned theorem for solution of the
problem on a radial dipole placed outside the sphere.
Thus let there be a sphere with
r = a placed into a spherical
coordinate system with the center
at the origin.
At a
distance
f from the sphere center
(f > a) we place a dipole
with the magnetic moment
M (Figure 1).
It is known that the dipole potential in "its own" coordinate system is
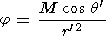 | (2) |
Being displaced at a distance f from the origin, this dipole will have the potential
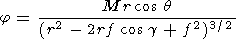 | (3) |
We use the fact that r cos q = r' cos q' and g is the angle between the radius vector r and vector OA= f. If the azimuth w is measured from the line OA, then
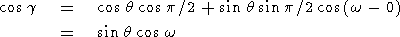 | (4) |
Using (1), we write (omitting the implicit arguments q, w of j for simplicity)
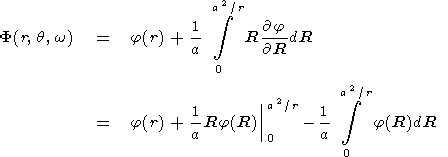 | (5) |
Substituting (3) into this expression and making a simple integration, we obtain
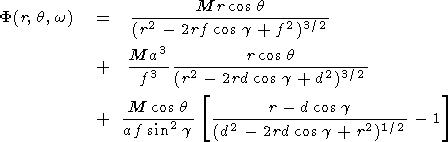 | (6) |
(We introduced an inversion point relative the d = a2/f sphere.)
The analysis of this formula shows that the sphere influence leads to an appearance within the sphere in the inversion point d of the mapped dipole with the power Ma3/f3 < M and some additional source within the sphere described by the third term.
Finally, we consider our main problem of a dipole inside the sphere placed at the distance d from the sphere center (d < a). Solving the external problem, we saw that the dipole outside the sphere induces within the sphere a mapped dipole and an additional field. In order to compensate this additional field we have to assume that outside the sphere there should exist some additional field source besides the dipole. Thus let there be a dipole with the power M1 described by the potential j0(r,q,w) outside the sphere at the distance f and some source described by the potential j1(r,q,w). (As earlier, we use fd = a2.) Then from the Veiss theorem,
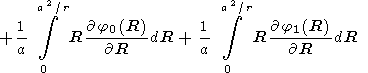 | (7) |
The first integral on the right-hand side can be broken down into
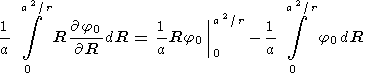 | (8) |
To find the potential j1, we require that
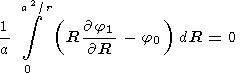 | (9) |
for all values of r>a, meaning that the integrand must equal zero and hence
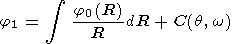 | (10) |
The integral obtained is indefinite; therefore one can replace R by r.
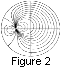
Therefore
 | (11) |
We chose the constant
C(q,w)
in such a form that there
is no singularity at
g 0.
0.
 Thus, if a single dipole with the moment
M
[M = M1(a/f)3] is
placed inside the sphere, then the total potential is equal to
Thus, if a single dipole with the moment
M
[M = M1(a/f)3] is
placed inside the sphere, then the total potential is equal to
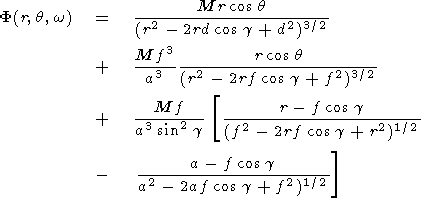 | (12) |
The solutions obtained are easily generalized for the case when the inner dipole axis is inclined from the normal to the equatorial plane by an angle q0 and rotates around the vertical axis with an angular velocity W.
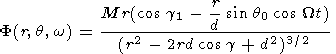 |
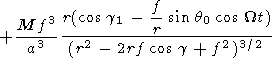 |
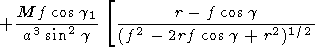 |
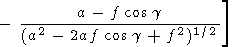 |
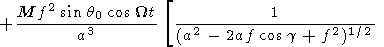 |
 |
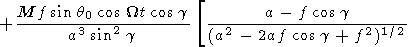 |
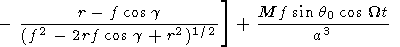 |
 | (13) |
Here cos g = sin q cos w and cos g1 = cos q cos q0 + sin q sin q0 cos (Wt - w). Figure 2 shows the cross section of the sphere with the locked dipole calculated by (13) with 2t = p. At q0 = 0 (when the inclination is absent), (13) transforms into (12). For the sake of simplicity, we consider again the expression (12). Two free parameters are present there: a and d (or f ).
The parameter d is unambiguously connected with the cusp latitude. This connection is easily obtained if the Bq component of the magnetic field at the boundary of the spherical cover in the cusp point is taken to be zero.
For the central and frontal parts of the Earth's magnetosphere one can use this analytical approximation. In reality, the magnetosphere is aligned in the antisolar direction; therefore for distant magnetospheric regions this model does not work.
In this paper a simple analytical model of the Earth's magnetosphere which may be used for description of the inner magnetosphere and polar cusps is suggested. A formula for the distance Rs from the dipole center to the subsolar critical point is also suggested.
Fairfield, D. H., Average and unusual locations of the Earth's magnetopause and bow shock, J. Geophys. Res., 76, 6700, 1971.
Krymskiy, G. F., and Yu. A. Romashchenko, Magnetohydrodynamical model of magnetosphere, Issled. Geomagn. Aeron. Fiz. Solntsa (in Russian), 36, 174, 1975.
Milne-Thomson, L. M., Theoretical Hydrodynamics, St. Martin's Press, London, 1964.
Pudovkin, M. I., et al., Physical Basis of Magnetospheric Disturbance Prognosis (in Russian), p. 312, Nauka, Leningrad, 1977.
Sergeev, V. A., and N. A. Tsyganenko, The Earth's Magnetosphere, (in Russian) Nauka, Moscow, 1980.
Tsyganenko, N. A., Quantitative models of the magnetospheric magnetic field: Method and results, Space Sci. Rev., 54, 75, 1990.