International Journal of Geomagnetism and Aeronomy
Vol 2, No. 1, June 2000
ULF waves in the magnetosheath
R. E. Denton
Physics and Astronomy Department, Dartmouth College,
Hanover, New Hampshire
Contents
Abstract
The magnetosheath
is both a conduit into the magnetosphere for upstream
waves and a source region for new waves.
The most structure in wave properties is observed for
plasma convecting from the quasi-perpendicular bowshock
(with interplanetary magnetic field roughly perpendicular
to the shock normal). The
magnetosonic (fast) mode
and Alfvén waves are observed in the quasi-perpendicular
bowshock. Just downstream of the bowshock,
Alfvén/ion cyclotron
waves are commonly observed. Velocity space
anisotropies generated at the bowshock and within the magnetosheath
proper drive mirror and ion cyclotron waves; these waves can be
significantly modified as they approach the magnetopause where the
plasma beta decreases. Mirror waves can pile up in front of the
magnetopause, thus acquiring a finite phase velocity relative to the
flow. Waves previously identified as the ion acoustic (slow) mode
due to their phase velocity are
best identified as the mirror mode (it is possible that
there is some coupling between the two). Ion cyclotron
waves are observed in the depletion layer, if it exists, close to
the magnetopause. Broadband transverse waves
are observed in the vicinity of the magnetopause; these may be
caused by reconnection or mode conversion to kinetic Alfvén
waves.
Waves recently identified
as the quasi-parallel mirror mode (with wave vector roughly parallel to
the background magnetic field) probably consist of a mixture of
the conventional mirror mode
(quasi-perpendicular wave vector) and Alfvén
waves. Quasi-parallel shock conditions typically
lead to high beta large amplitude turbulent fluctuations which are,
with some modification, transmitted through the magnetosheath from
the foreshock to the magnetosphere.
The growth and propagation
of magnetosheath waves is strongly affected by spatial inhomogeneity.
Magnetosheath waves have an appreciable feedback on the macroscopic
plasma, affecting the temperature ratio and possibly reconnection
and transport at the magnetopause.
1. Introduction
The magnetosheath is the region of interaction between the
solar wind plasma and the Earth's magnetic field.
The magnetosheath exhibits large inhomogeneity due to the stress
of the solar wind dynamic pressure.
Since this pressure is pushing nearly continuously on the magnetopause,
the structure of the magnetosheath
is in the roughest approximation time stationary. This makes it
an ideal region for studying the effects of such inhomogeneity.
Inhomogeneity has
a crucial effect on the generation and propagation of ultra low
frequency (ULF) waves. In turn, ULF waves have significant
feedback on the macroscopic plasma.
The purpose of this paper is to review what we know about magnetosheath
ULF waves. Our presentation is not totally
comprehensive, but rather expresses our view of
major issues in ULF wave studies as presented at the 1999 IAGA
meeting
[Denton, 1999].
Two recent reviews of a similar nature have been given by
Schwartz et al. [1996] and
Song and Russell [1997].
An outline of our paper is as
follows: In section 2, we discuss methods of mode identification.
In section 3, we discuss some important properties of the
magnetosheath which relate to the generation and propagation of
ULF waves.
In section 4, we discuss ULF waves in the magnetosheath when the
upstream conditions are quasi-parallel,
and in section 5, we discuss ULF waves in the
magnetosheath when the upstream conditions are quasi-perpendicular.
Finally, we have a summary in section 6.
2. Methods of Mode Identification
Since the mode properties can be strongly modified by the
kinetic nature of a plasma, it is best to use kinetic theory when
making comparisons with observation for the purpose of mode
identification
[Denton et al., 1995a;
Krauss-Varban et al., 1994].
At frequency
f 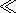 Fcp, where
Fcp is the
proton cyclotron
frequency, up to four distinct modes can propagate in a relatively
isotropic plasma: the three waves corresponding to the normal
modes of MHD theory and the mirror mode. The mirror mode has
zero phase velocity in a homogeneous plasma (though it can acquire
a finite phase velocity when there is inhomogeneity
[Johnson and Cheng, 1997]).
The three modes with finite phase velocity are the
magnetosonic/fast/whistler mode, the
Alfvén/ion-cyclotron mode,
and the ion-acoustic/slow/sound mode.
The first term listed
(i.e., "magnetosonic,'' "Alfvén,'' and
"ion acoustic'')
represents our preferred notation
[Denton et al., 1995a]
and the
other terms have been used by other authors
[for example,
Krauss-Varban et al., 1994].
The terms "fast'' and "slow'' here are
appropriate descriptions of
the phase speed of the respective waves at low
parallel beta
b||p
Fcp, where
Fcp is the
proton cyclotron
frequency, up to four distinct modes can propagate in a relatively
isotropic plasma: the three waves corresponding to the normal
modes of MHD theory and the mirror mode. The mirror mode has
zero phase velocity in a homogeneous plasma (though it can acquire
a finite phase velocity when there is inhomogeneity
[Johnson and Cheng, 1997]).
The three modes with finite phase velocity are the
magnetosonic/fast/whistler mode, the
Alfvén/ion-cyclotron mode,
and the ion-acoustic/slow/sound mode.
The first term listed
(i.e., "magnetosonic,'' "Alfvén,'' and
"ion acoustic'')
represents our preferred notation
[Denton et al., 1995a]
and the
other terms have been used by other authors
[for example,
Krauss-Varban et al., 1994].
The terms "fast'' and "slow'' here are
appropriate descriptions of
the phase speed of the respective waves at low
parallel beta
b||p  8 pp||p/B02
in CGS units, where
p||p is the proton pressure parallel to
B,
and
B is the magnetic field.
At high beta, what we call the "slow'' mode sometimes has the
largest phase
velocity
[Denton et al., 1995a;
Krauss-Varban et al., 1994].
Our use of the terms "slow'' and "fast'' here agrees with
the nomenclature of
Krauss-Varban et al. [1994],
which was
designed to use the same term to refer to the wave with similar
fluctuations (transport ratios),
regardless of phase speed. On the other hand,
Gary and Winske [1992]
and
Lacombe et al. [1992, 1995]
have retained the use of "slow'' and "fast'' to refer explicitly
to phase speed. (It is easy to see why we would prefer not to
use these terms.)
8 pp||p/B02
in CGS units, where
p||p is the proton pressure parallel to
B,
and
B is the magnetic field.
At high beta, what we call the "slow'' mode sometimes has the
largest phase
velocity
[Denton et al., 1995a;
Krauss-Varban et al., 1994].
Our use of the terms "slow'' and "fast'' here agrees with
the nomenclature of
Krauss-Varban et al. [1994],
which was
designed to use the same term to refer to the wave with similar
fluctuations (transport ratios),
regardless of phase speed. On the other hand,
Gary and Winske [1992]
and
Lacombe et al. [1992, 1995]
have retained the use of "slow'' and "fast'' to refer explicitly
to phase speed. (It is easy to see why we would prefer not to
use these terms.)
The linear modes are defined on dispersion surfaces as a function
of the wave vector
k.
One can distinguish whether the modes are approximately
quasi-parallel ( k approximately parallel to
B ) or
quasi-perp ( k approximately perpendicular to
B )
[Denton et al., 1995a].
Both the magnetosonic/fast/whistler and Alfvén/ion-cyclotron
modes
are Alfvén-like for parallel propagation.
In that case, the
magnetosonic/fast/whistler mode is right hand polarized while
the Alfvén/ion-cyclotron mode is left
hand polarized.
Both of these waves become more and more linearly
polarized as
k turns away from
B.
As discussed by
Schwartz et al. [1996],
identification of
wave modes is hampered by a number of factors. Most of the
theory is based on linear homogeneous theory,
whereas the observed modes are observed in an inhomogeneous
medium and are often significantly nonlinear.
Perhaps the greatest problem is that there can be a mixture
of different modes.
Denton et al. [1998]
found that in
a number of cases, the identification of the wave mode was
not certain.
Methods of mode identification use transport ratios, phase angle
relations, and polarization information (see review by
Schwartz et al. [1996]
for an extensive list of transport
ratios with references).
Gary and Winske [1992]
introduced the term
"transport ratios'' to denote dimensionless ratios of the squares of
fluctuating field and plasma quantities.
One of the most commonly used transport ratios is the magnetic
compressibility, the ratio of
parallel to total magnetic fluctuations
 | (1) |
where the angular bracket indicates an average (often calculated
using the power spectrum at a particular frequency).
This is expected to be large for the quasi-perpendicular
magnetosonic (fast) mode and mirror mode, but small for the
Alfvén mode.
A quantity functionally
equivalent to
CB was used by
Anderson and Fuselier [1993]
to distinguish Alfvén (ion cyclotron)
waves from the mirror mode.
 Two other useful transport ratios are
the compressibility
Cp
Two other useful transport ratios are
the compressibility
Cp
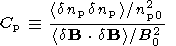 | (2) |
where
dnp and
np0 are the fluctuating and equilibrium
(slow time scale)
proton density, respectively, and
B0 is the equilibrium
magnetic field, and the Alfvén ratio
RAp
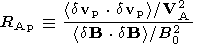 | (3) |
where
d vp and
VA are the fluctuating proton velocity
and equilibrium Alfvén speed
 B0 / 4 pmp
np in CGS units, where
mp is the proton mass.
Figure 1
is a dramatic demonstration of the effectiveness of these transport
ratios for mode identification.
Figure 1
shows the
transport ratios
Cp and
RAp obtained for waves
observed near the magnetopause (crosses).
These waves were thought to be
either the mirror mode or the ion acoustic (slow)
mode based on the relative
phase in
dnp and
dB|| (not shown). Based on the
transport ratios in Figure 1,
it is clear that these
waves should be identified as the mirror mode.
B0 / 4 pmp
np in CGS units, where
mp is the proton mass.
Figure 1
is a dramatic demonstration of the effectiveness of these transport
ratios for mode identification.
Figure 1
shows the
transport ratios
Cp and
RAp obtained for waves
observed near the magnetopause (crosses).
These waves were thought to be
either the mirror mode or the ion acoustic (slow)
mode based on the relative
phase in
dnp and
dB|| (not shown). Based on the
transport ratios in Figure 1,
it is clear that these
waves should be identified as the mirror mode.
A second important determining factor for wave identification
is
based on the phase difference between various fluctuating quantities.
For the magnetosheath data of Figure 1,
dnp and
dB|| were shown to be 180
o out of
phase. Such a phase relation exists for the quasi-perpendicular
mirror and
ion acoustic (slow) modes, but
dnp and
dB|| should be in phase for the
quasi-perpendicular
magnetosonic (fast) mode.
Polarization information can be very useful for determining the
wave mode. In the Earth's ion foreshock (the region just outside
the bowshock where ions reflected off the bowshock are observed),
Alfvén-like waves are often observed.
These may be left or right
hand polarized (the latter is the
quasi-parallel magnetosonic mode in our nomenclature), where the
handedness indicates the direction of rotation of fluctuating
quantities about the equilibrium magnetic field.
In order to determine polarization, it is most beneficial to have
multi-spacecraft observations.
Russell et al. [1987]
used simultaneous observations by the ISEE 2 and AMPTE/UKS
spacecraft to the determine polarization of foreshock waves.
Blanco-Cano and Schwartz [1997],
using single spacecraft
data, measured a number of transport ratios to identify these waves;
unfortunately these transport ratios did not enable them to
distinguish the waves. Their identification was based mainly on a
determination of polarization which depended on minimum variance
analysis (to determine the direction of
 k ) and properties
of the cross-helicity
which enabled them to eliminate the sign ambiguity (
k ) and properties
of the cross-helicity
which enabled them to eliminate the sign ambiguity ( 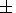 )
[Blanco-Cano and Schwartz, 1997].
Using the minimum variance direction for magnetic fluctuations is
a common method to infer the direction of
k (based on
Faraday's law), but can be misleading if there is a mixture of
modes (see
[Denton et al., 1996]).
Use of multi-spacecraft
data is therefore highly desirable for determining wave
polarization.
)
[Blanco-Cano and Schwartz, 1997].
Using the minimum variance direction for magnetic fluctuations is
a common method to infer the direction of
k (based on
Faraday's law), but can be misleading if there is a mixture of
modes (see
[Denton et al., 1996]).
Use of multi-spacecraft
data is therefore highly desirable for determining wave
polarization.
3. Properties of the Magnetosheath
The particular properties of the magnetosheath play a large role
in the generation, propagation, and modification of magnetosheath
ULF waves. Whether the upstream conditions are
"quasi-perpendicular'' or
"quasi-parallel'' depends on the direction of the
interplanetary magnetic field (IMF) when the solar wind plasma
reaches the bowshock. (The use of "quasi-perpendicular'' and
"quasi-parallel'' here should not be confused with their
use to describe the relative orientation of
k and
B in
"quasi-perpendicular'' and "quasi-parallel'' wave propagation.)
By upstream conditions, we mean then that if we were to follow the
convecting plasma backward in time, the IMF would be
"quasi-perpendicular'' or "quasi-parallel'' at the time that the
plasma crossed the bowshock. The plasma convects through the
magnetosheath to its present position maintaining some general
characteristics resulting from that orientation.
The plasma with quasi-perpendicular upstream conditions (when the
IMF is roughly aligned with the bowshock,
or perpendicular to the bowshock normal)
exhibits the most regular structure. The value of
B0 typically
increases from the bowshock to the magnetopause. Sometimes,
particularly for low magnetic shear
[Phan et al., 1994],
the density
np0 decreases near the magnetopause;
this region of decrease
is sometimes called the plasma depletion layer. Field lines in
the magnetosheath drape around the magnetopause leading to field
line curvature.
 When the upstream conditions are quasi-perpendicular, the plasma
typically exhibits temperature anisotropy
T
When the upstream conditions are quasi-perpendicular, the plasma
typically exhibits temperature anisotropy
T p / T|
p > 1,
where
T
p / T|
p > 1,
where
T p and
T||p are the proton temperatures respectively
perpendicular and parallel to
B [Phan et al., 1994].
The region close to the bowshock exhibits a large
anisotropy due to the fact that ions entering the magnetosheath
through the bowshock roughly have their large bulk flow (solar wind)
velocity converted into a (perpendicular) gyrovelocity
[Sckopke et al., 1990].
Other effects leading to temperature anisotropy are compression of
flux tubes as they press up against the magnetopause and their
lengthening as they drape around the magnetopause
(see Figure 2)
[Denton et al., 1994c].
How these effects lead to the development of temperature anisotropy
can be easily seen from the double adiabatic
equations
[Chew et al., 1956],
which can be expressed as
T
p and
T||p are the proton temperatures respectively
perpendicular and parallel to
B [Phan et al., 1994].
The region close to the bowshock exhibits a large
anisotropy due to the fact that ions entering the magnetosheath
through the bowshock roughly have their large bulk flow (solar wind)
velocity converted into a (perpendicular) gyrovelocity
[Sckopke et al., 1990].
Other effects leading to temperature anisotropy are compression of
flux tubes as they press up against the magnetopause and their
lengthening as they drape around the magnetopause
(see Figure 2)
[Denton et al., 1994c].
How these effects lead to the development of temperature anisotropy
can be easily seen from the double adiabatic
equations
[Chew et al., 1956],
which can be expressed as
T p
p 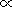 A-1 and
T||p
A-1 and
T||p 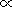 L-2,
where
A and
L are the area and length of a flux tube, respectively
[Denton et al., 1994c].
(While double adiabatic theory does not by itself adequately describe
temperature evolution in space plasmas, a modified form of the
theory including energy exchange due to ion cyclotron waves has been
relatively successful
[Denton et al., 1994c, 1995b].)
Temperature anisotropy which develops when the upstream conditions
are quasi-perpendicular
leads to the growth of ion cyclotron and mirror waves
[Anderson et al., 1994].
L-2,
where
A and
L are the area and length of a flux tube, respectively
[Denton et al., 1994c].
(While double adiabatic theory does not by itself adequately describe
temperature evolution in space plasmas, a modified form of the
theory including energy exchange due to ion cyclotron waves has been
relatively successful
[Denton et al., 1994c, 1995b].)
Temperature anisotropy which develops when the upstream conditions
are quasi-perpendicular
leads to the growth of ion cyclotron and mirror waves
[Anderson et al., 1994].
 When the upstream conditions are quasi-parallel,
(so that the IMF is roughly
aligned with the bowshock normal), the plasma typically has large
plasma beta and is very turbulent.
The high beta conditions arise from the fact that
the shocked solar wind plasma is compressed, leading to
large increase in plasma pressure, but the quasi-parallel magnetic
field is not (this is precisely true only when the IMF is
exactly quasi-parallel). When the upstream conditions are
quasi-parallel,
the magnetic field exhibits large amplitude fluctuations which
accompany the fluctuations in thermal plasma pressure, the latter
of which lead to the dominant force density in the high beta
magnetosheath.
The direction of the magnetic field is then ill-defined, as are
the separate values of
T
When the upstream conditions are quasi-parallel,
(so that the IMF is roughly
aligned with the bowshock normal), the plasma typically has large
plasma beta and is very turbulent.
The high beta conditions arise from the fact that
the shocked solar wind plasma is compressed, leading to
large increase in plasma pressure, but the quasi-parallel magnetic
field is not (this is precisely true only when the IMF is
exactly quasi-parallel). When the upstream conditions are
quasi-parallel,
the magnetic field exhibits large amplitude fluctuations which
accompany the fluctuations in thermal plasma pressure, the latter
of which lead to the dominant force density in the high beta
magnetosheath.
The direction of the magnetic field is then ill-defined, as are
the separate values of
T p
and
T||p.
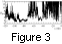
A spacecraft within
the magnetosheath may observe alternating periods of time for which
the magnetosheath exhibits quasi-perpendicular or quasi-parallel-like
upstream conditions, as illustrated in
Figure 3,
where the periods of large
b||p
p
and
T||p.
A spacecraft within
the magnetosheath may observe alternating periods of time for which
the magnetosheath exhibits quasi-perpendicular or quasi-parallel-like
upstream conditions, as illustrated in
Figure 3,
where the periods of large
b||p 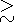 10 represent
quasi-parallel upstream conditions. Another diagnostic for
quasi-parallel upstream conditions is the presence of elevated
fluxes of energetic He2+ [Fuselier et al., 1991].
10 represent
quasi-parallel upstream conditions. Another diagnostic for
quasi-parallel upstream conditions is the presence of elevated
fluxes of energetic He2+ [Fuselier et al., 1991].
4. Waves for Quasi-Parallel Upstream Conditions
Typically, broad band turbulent waves are observed when the
upstream conditions are quasi-parallel,
with power peaking in the Pc3-4
range (period from 10-150 s)
[Engebretson et al., 1991,
and references therein;
see their Plate 4 for an example of broad band turbulence].
These waves are thought to be caused, at least in part, by
the ion foreshock waves mentioned in Section 2
(see papers in
[Engebretson et al., 1994],
particularly
[Krauss-Varban, 1994]).
They are also
generally thought to be the source of the toroidal Alfvén
wave (with magnetic fluctuation in the azimuthal direction)
harmonics observed in the magnetosphere
[Anderson, 1993, and references therein],
though the path the wave power takes to
get to the magnetosphere is still a matter of debate
(Mark Engebretson, private communication, 1999).
A statistical survey by
Anderson and Fuselier [1993]
showed that Alfvén/ion cyclotron and mirror
waves could
be observed when the upstream conditions are quasi-parallel, though the
most likely situation was to observe broadband waves.
Even when there is no explicit evidence for the existence of ion
cyclotron waves amid the broad band turbulence, there is indirect
evidence that ion cyclotron waves are present
(anisotropy-beta correlation; see Section 5.2)
[Fuselier et al., 1994].
Little has been done theoretically to describe the high beta
waves. A recent paper applies an approach based on
magnetohydrodynamics (MHD)
[Song et al., 1998],
though it
may be difficult to justify the use of MHD and the assumption
that the equilibrium magnetic field is steady.
5. Waves for Quasi-Perpendicular Upstream Conditions
When the upstream conditions are
quasi-perpendicular,
the magnetosheath exhibits more regularity
in macroscopic structure and in the ULF waves observed.
We consider the plasma as it convects from the bowshock
to the magnetopause and the characteristic waves of each region.
One should keep in mind that not all
the waves described here may be
present at any one time.
5.1. Within the Bowshock
Since the bowshock is itself a manifestation of the
quasi-perpendicular magnetosonic (fast) mode reflecting off
the magnetopause, it is not too
surprising that
Lacombe et al. [1992]
identified this
wave within the bowshock structure. They also identified
both quasi-parallel and quasi-perpendicular Alfvén
waves;
these may be due to fluctuations at the bowshock.
5.2. Outer Magnetosheath (Just Downstream
From
the Bowshock)
A large proton temperature anisotropy
T p
p 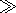 T||p develops
just downstream of the bowshock
[Sckopke et al., 1990, and
references therein]
due to the conversion of solar wind bulk
flow energy into energy associated with the (perpendicular)
gyromotion. An anisotropic plasma can be unstable to the ion
cyclotron or mirror instabilities
[Gary, 1993].
The instability of the plasma increases with increasing beta
b||p and temperature ratio
T
T||p develops
just downstream of the bowshock
[Sckopke et al., 1990, and
references therein]
due to the conversion of solar wind bulk
flow energy into energy associated with the (perpendicular)
gyromotion. An anisotropic plasma can be unstable to the ion
cyclotron or mirror instabilities
[Gary, 1993].
The instability of the plasma increases with increasing beta
b||p and temperature ratio
T p / T|
p.
At low
b||p,
a large value of
T
p / T|
p.
At low
b||p,
a large value of
T p / T|
p is required for
instability, while at high
b||p,
a plasma can be unstable
with a low value of
T
p / T|
p is required for
instability, while at high
b||p,
a plasma can be unstable
with a low value of
T p / T|
p.
Whether the ion cyclotron or mirror mode is dominant
depends on the values of
b||p and
T
p / T|
p.
Whether the ion cyclotron or mirror mode is dominant
depends on the values of
b||p and
T p / T|
p.
Generally the ion cyclotron mode is favored for low
b||p and large
T
p / T|
p.
Generally the ion cyclotron mode is favored for low
b||p and large
T p / T|
p,
while the mirror mode is favored for high
b||p and low
T
p / T|
p,
while the mirror mode is favored for high
b||p and low
T p / T|
p [Denton et al., 1994a;
Gary et al., 1993].
While
T
p / T|
p [Denton et al., 1994a;
Gary et al., 1993].
While
T p increases steeply
across the quasi-perpendicular
bowshock,
does not. The result is that
T
p increases steeply
across the quasi-perpendicular
bowshock,
does not. The result is that
T p / T|
p is large and
b||p
p / T|
p is large and
b||p 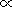 T||p relatively low just downstream of
the bowshock so that ion cyclotron waves naturally grow.
T||p relatively low just downstream of
the bowshock so that ion cyclotron waves naturally grow.
 Figure 4
demonstrates the growth of ion cyclotron waves in the post bowshock
region. There are two bowshock crossings in Figure 4;
we concentrate on the first one at 0655 UT.
Following this crossing,
T
Figure 4
demonstrates the growth of ion cyclotron waves in the post bowshock
region. There are two bowshock crossings in Figure 4;
we concentrate on the first one at 0655 UT.
Following this crossing,
T p has become
very large, while
T||p has increased, but not
nearly as much. Consequently
T
p has become
very large, while
T||p has increased, but not
nearly as much. Consequently
T p / T|
p is very large.
Ion cyclotron waves have polarization which varies from left hand
polarized for parallel ( k
p / T|
p is very large.
Ion cyclotron waves have polarization which varies from left hand
polarized for parallel ( k  B )
propagation to
nearly linearly polarized for highly oblique waves
[Denton et al, 1993].
The growth of transverse wave power
with more power in the left hand polarized waves
PL than in right hand polarized waves
PR, which occurs
at about 0657 UT
is indicative of the presence of ion cyclotron
waves.
B )
propagation to
nearly linearly polarized for highly oblique waves
[Denton et al, 1993].
The growth of transverse wave power
with more power in the left hand polarized waves
PL than in right hand polarized waves
PR, which occurs
at about 0657 UT
is indicative of the presence of ion cyclotron
waves.
Sckopke et al. [1990]
observed a "double humped,''
or bifurcated
structure in wave power as a function of frequency.
Brinca et al. [1990]
interpreted the bifurcated spectra
as being due to
the combination of a core and beam component of protons, but it
is possible that the bifurcated spectra
result from the presence of He2+ as discussed in
Section 5.4.3.
 At the same time that the ion cyclotron waves grow large in
Figure 4
(0657 UT), there is a transfer of energy
from
T
At the same time that the ion cyclotron waves grow large in
Figure 4
(0657 UT), there is a transfer of energy
from
T p
to
T||p so that
T
p
to
T||p so that
T p / T|
p is greatly reduced. The
process by which this occurs is called pitch angle scattering
[Kennel and Petschek, 1966].
Figure 5
shows that the values of
T
p / T|
p is greatly reduced. The
process by which this occurs is called pitch angle scattering
[Kennel and Petschek, 1966].
Figure 5
shows that the values of
T p / T|
p observed by the
AMPTE/CCE spacecraft in the magnetosheath line up roughly along
a curve which was first expressed
[Anderson et al., 1994]
as
p / T|
p observed by the
AMPTE/CCE spacecraft in the magnetosheath line up roughly along
a curve which was first expressed
[Anderson et al., 1994]
as
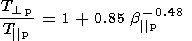 | (4) |
and that this curve is not far above the marginal stability
condition for ion cyclotron waves
[Anderson et al., 1994;
Denton et al., 1994c;
Gary et al., 1993, 1994].
While the value of
T p / T|
p may lie under this curve
[Denton et al., 1995b;
Phan et al., 1994],
it is rare that
the value of
(4) is significantly exceeded; certainly
it is not exceeded greatly for any period of time exceeding the
growth time of ion cyclotron waves. Thus it appears that
ion cyclotron waves regulate the temperature ratio.
p / T|
p may lie under this curve
[Denton et al., 1995b;
Phan et al., 1994],
it is rare that
the value of
(4) is significantly exceeded; certainly
it is not exceeded greatly for any period of time exceeding the
growth time of ion cyclotron waves. Thus it appears that
ion cyclotron waves regulate the temperature ratio.
While it seems clear that the transverse waves observed in
Figure 4
are caused by the ion cyclotron
instability, Alfvén waves are sometimes
observed in the outer
magnetosheath when
T p / T|
p is low
[Denton et al., 1998].
These waves could have resulted from
fluctuations at the bowshock, or might have been generated by
ion cyclotron waves upstream of their observation.
p / T|
p is low
[Denton et al., 1998].
These waves could have resulted from
fluctuations at the bowshock, or might have been generated by
ion cyclotron waves upstream of their observation.
Lacombe et al. [1992]
identified both Alfvén (ion cyclotron)
waves and mirror mode waves (see Section 5.3) in the outer
magnetosheath.
5.3. Middle Magnetosheath
 Due to the increase in
T||p caused by the ion cyclotron waves
in the outer magnetosheath (Figure 4), the value of
b||p
Due to the increase in
T||p caused by the ion cyclotron waves
in the outer magnetosheath (Figure 4), the value of
b||p 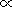 T||p increases. As a result of the increased
value of
b||p and decreased value
of
T
T||p increases. As a result of the increased
value of
b||p and decreased value
of
T p / T|
p,
the
plasma conditions become more favorable to the growth of the mirror
mode. The mirror mode has been identified in the magnetosheath
by a number of authors
[Anderson et al., 1994;
Fazakerley and Southwood, 1994;
Hubert, 1994;
Hubert et al., 1989;
Lacombe et al., 1995;
Tsurutani et al., 1982].
While in Figure 4,
the ion cyclotron mode
appears to remain dominant downstream of the bowshock
(we never observe in Figure 4 a magnetopause crossing;
we may always be in the outer magnetosheath), the normal
situation seems to be that the mirror mode has the dominant wave
power throughout most of the magnetosheath.
Figure 6
shows out of phase fluctuations of
B and electron density
Ne which were identified as the mirror mode
[Anderson et al., 1994].
p / T|
p,
the
plasma conditions become more favorable to the growth of the mirror
mode. The mirror mode has been identified in the magnetosheath
by a number of authors
[Anderson et al., 1994;
Fazakerley and Southwood, 1994;
Hubert, 1994;
Hubert et al., 1989;
Lacombe et al., 1995;
Tsurutani et al., 1982].
While in Figure 4,
the ion cyclotron mode
appears to remain dominant downstream of the bowshock
(we never observe in Figure 4 a magnetopause crossing;
we may always be in the outer magnetosheath), the normal
situation seems to be that the mirror mode has the dominant wave
power throughout most of the magnetosheath.
Figure 6
shows out of phase fluctuations of
B and electron density
Ne which were identified as the mirror mode
[Anderson et al., 1994].
Alfvén (ion cyclotron) waves are also
sometimes observed in
the middle magnetosheath.
Some evidence suggests that the ion cyclotron waves may be the
dominant cause of temperature anisotropy regulation even when the
mirror mode is the dominant wave
[McKean et al., 1992, 1994];
however, except for very low
b||p, the mirror mode marginal
stability criterion is similar to
(4) indicating that the mirror mode could also possibly
play a role.
Lacombe et al. [1995]
claims to identify the He2+ cutoff mode (see also
[Denton et al., 1994a]
for pictures
of the dispersion surface) which exists due to the presence of the
heavy ion.
5.4. Inner Magnetosheath (Close to Magnetopause)
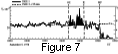 Figure 7
shows a density enhancement observed by the ISEE 1 spacecraft in
front of the magnetopause on September 5, 1978. Based on such
observations,
Song et al. [1990b, 1992a]
hypothesized that the
enhancement was due to an ion acoustic (slow) mode
shock in front of the magnetopause.
Song et al. [1992b, 1994]
went on to identify ion acoustic
(slow)
waves in the region of the magnetosheath close to the
magnetopause. The observed waves had magnetic fluctuations out
of phase with density fluctuations. The waves could thus be
the mirror mode (Figure 6)
or the ion acoustic mode. The
identification as the ion acoustic mode was based on the fact that the
observed waves had a finite upstream phase velocity in the rest
frame of the plasma. (Recall that the mirror mode has zero
frequency in a homogeneous plasma.)
Figure 7
shows a density enhancement observed by the ISEE 1 spacecraft in
front of the magnetopause on September 5, 1978. Based on such
observations,
Song et al. [1990b, 1992a]
hypothesized that the
enhancement was due to an ion acoustic (slow) mode
shock in front of the magnetopause.
Song et al. [1992b, 1994]
went on to identify ion acoustic
(slow)
waves in the region of the magnetosheath close to the
magnetopause. The observed waves had magnetic fluctuations out
of phase with density fluctuations. The waves could thus be
the mirror mode (Figure 6)
or the ion acoustic mode. The
identification as the ion acoustic mode was based on the fact that the
observed waves had a finite upstream phase velocity in the rest
frame of the plasma. (Recall that the mirror mode has zero
frequency in a homogeneous plasma.)
 Whether or not density enhancements like that in Figure 7
are related to a standing ion acoustic (slow mode) front or shock
[Song et al., 1990b, 1992a]
is still a matter of debate;
however, the weight of evidence is that the waves observed by
Song et al. [1994]
are the mirror mode, not the ion acoustic
mode. The linear ion acoustic mode is strongly damped, as
is well
known, but it was argued that nonlinear effects might allow the
mode to persist
[Song et al., 1994].
Denton et al. [1995a]
showed that the values
of the transport ratios strongly indicated the mirror mode
(see Figure 1).
The problem remained, however, to
explain the finite phase velocity of the waves.
Omidi and Winske [1995]
showed using a one dimensional hybrid code
simulation of the magnetosheath that mirror modes convecting from
the bowshock pile up at the magnetopause; they are unable to penetrate
to the low beta magnetosphere (see Figure 8).
Whether or not density enhancements like that in Figure 7
are related to a standing ion acoustic (slow mode) front or shock
[Song et al., 1990b, 1992a]
is still a matter of debate;
however, the weight of evidence is that the waves observed by
Song et al. [1994]
are the mirror mode, not the ion acoustic
mode. The linear ion acoustic mode is strongly damped, as
is well
known, but it was argued that nonlinear effects might allow the
mode to persist
[Song et al., 1994].
Denton et al. [1995a]
showed that the values
of the transport ratios strongly indicated the mirror mode
(see Figure 1).
The problem remained, however, to
explain the finite phase velocity of the waves.
Omidi and Winske [1995]
showed using a one dimensional hybrid code
simulation of the magnetosheath that mirror modes convecting from
the bowshock pile up at the magnetopause; they are unable to penetrate
to the low beta magnetosphere (see Figure 8).
Subsequently,
Johnson and Cheng [1997]
solved for the mirror eigenmodes in a model
magnetosheath and found that due to the inhomogeneity, the mirror
mode acquires a finite phase velocity near the magnetopause.
(Their theory did not include coupling to the ion acoustic mode;
it is possible that there is coupling between the two modes.)
Finally,
Lin et al. [1998]
examined additional phase relations
between field components that indicated that the waves of
Song et al. [1994]
were really the mirror mode.
(The linear theory of
Lin et al. [1998]
is at best of
doubtful relevance to the mirror mode phase relations they use,
but the mirror mode phase relations are verified using hybrid
code simulations. We are forced, however, to accept their linear
fluid theory for the ion acoustic mode phase relations.)
5.4.2. Quasi-Parallel Mirror Mode.
In addition to identifying the ordinary quasi-perpendicular
mirror mode
( k approximately
 B ),
Denton et al. [1995a]
identified the quasi-parallel mirror mode ( k approximately
B ),
Denton et al. [1995a]
identified the quasi-parallel mirror mode ( k approximately
 B ).
Denton et al. [1998]
reexamined the
identification of these waves and concluded that "the
quasi-parallel mirror mode may be observed in the inner
magnetosheath, but that identification is not certain.''
The technique of
Lin et al. [1998]
was used to
examine event number 7 of
Denton et al. [1998]
for a third
time (J. K. Chao, private communication, 1998).
There was mixed evidence for the mirror mode and the
Alfvén wave. It appears that both of these
modes may be
present simultaneously.
This makes the identification of the quasi-parallel mirror
mode very uncertain.
B ).
Denton et al. [1998]
reexamined the
identification of these waves and concluded that "the
quasi-parallel mirror mode may be observed in the inner
magnetosheath, but that identification is not certain.''
The technique of
Lin et al. [1998]
was used to
examine event number 7 of
Denton et al. [1998]
for a third
time (J. K. Chao, private communication, 1998).
There was mixed evidence for the mirror mode and the
Alfvén wave. It appears that both of these
modes may be
present simultaneously.
This makes the identification of the quasi-parallel mirror
mode very uncertain.
5.4.3. Ion Cyclotron Waves.
As mentioned earlier,
the magnetic field generally increases toward the magnetopause.
In addition, a region of depleted density
np, called the depletion
layer, may be present adjacent to the magnetopause.
If there is such a decrease in
np, there is usually also
a decrease in the parallel temperature
T||p. All these
factors lead to a decrease in
b||p as the magnetopause
is
approached,
and the decrease in
T||p leads to an increase in
T p / T|
p.
The combination of low
b||p and large
T
p / T|
p.
The combination of low
b||p and large
T p / T|
p is conducive to the growth of
ion cyclotron modes in the depletion layer, as discussed in
Section 5.2.
Fairfield [1976]
first identified ion cyclotron
waves in this region. More recent observations have been made by
Song et al. [1990a],
Anderson and Fuselier [1993]
and
Anderson et al. [1994]
( Song et al. did not regard the
transverse waves they observed as ion cyclotron waves).
p / T|
p is conducive to the growth of
ion cyclotron modes in the depletion layer, as discussed in
Section 5.2.
Fairfield [1976]
first identified ion cyclotron
waves in this region. More recent observations have been made by
Song et al. [1990a],
Anderson and Fuselier [1993]
and
Anderson et al. [1994]
( Song et al. did not regard the
transverse waves they observed as ion cyclotron waves).
 Figure 9
shows magnetic power spectra
measured by the AMPTE/CCE spacecraft
and magnetic field and density data measured by CCE and
AMPTE/IRM after a magnetopause crossing
at ~1300 UT observed by CCE.
At that time, the AMPTE/IRM spacecraft was
upstream in the solar wind. The IRM density and magnetic field
data shows that the decreased density and increased magnetic field
measured by CCE from 1300-1340 UT cannot be explained by upstream
temporal variations; CCE is therefore in the plasma depletion layer
at that time. To the left in Figure 9, the value of
b||p is lower (due to lower
proton density and
T||p (not shown)
and larger
B0 ). At the lowest values of
b||p, there is a
gap in the transverse power spectra at about 0.7 Hz; the gap
is close to the He
2+ (alpha particle) gyrofrequency
Fa. Moving
from lower to higher
b||p,
Figure 9
reveals a progression from
bifurcated transverse spectra above and below
Fa (B),
to
continuous transverse spectra extending across
Fa (C),
to
transverse spectra below
Fa (L),
to the simultaneous
presence of low frequency transverse power and parallel power
assumed to be associated with the mirror mode (LM), to just
parallel power (M)
[Anderson et al., 1994].
(There is no stop He2+ stop band due to the high temperature
of the He2+ ; see
[Denton et al., 1994a].)
Figure 9
shows magnetic power spectra
measured by the AMPTE/CCE spacecraft
and magnetic field and density data measured by CCE and
AMPTE/IRM after a magnetopause crossing
at ~1300 UT observed by CCE.
At that time, the AMPTE/IRM spacecraft was
upstream in the solar wind. The IRM density and magnetic field
data shows that the decreased density and increased magnetic field
measured by CCE from 1300-1340 UT cannot be explained by upstream
temporal variations; CCE is therefore in the plasma depletion layer
at that time. To the left in Figure 9, the value of
b||p is lower (due to lower
proton density and
T||p (not shown)
and larger
B0 ). At the lowest values of
b||p, there is a
gap in the transverse power spectra at about 0.7 Hz; the gap
is close to the He
2+ (alpha particle) gyrofrequency
Fa. Moving
from lower to higher
b||p,
Figure 9
reveals a progression from
bifurcated transverse spectra above and below
Fa (B),
to
continuous transverse spectra extending across
Fa (C),
to
transverse spectra below
Fa (L),
to the simultaneous
presence of low frequency transverse power and parallel power
assumed to be associated with the mirror mode (LM), to just
parallel power (M)
[Anderson et al., 1994].
(There is no stop He2+ stop band due to the high temperature
of the He2+ ; see
[Denton et al., 1994a].)
 The structure of the wave spectra displayed in Figure 9
was accounted for by
Denton et al. [1994c].
Their work
was based on a simple model of the magnetosheath which assumed
4% He2+ and incorporated the anisotropy-beta relation
(4); a Vlasov dispersion solver was used to solve for
the real and imaginary parts of the wave frequency. Figure 10
shows the main results of their model. Figure 10a
shows
that the ion cyclotron instability splits into two branches at low
parallel beta
b||p, one driven by the
temperature anisotropy of the
protons (marked "p'') and one driven by the temperature
anisotropy of the He2+ (alpha particles) (marked "
a '').
These two modes merge at high
b||p.
Figure 10b
shows the normalized growth rate for these two
modes and also for the mirror mode (which has zero real frequency, so
it does not appear in Figure 10a).
The letters "B,'' "C,'' "L,'' "LM,'' and "M'' in
Figure 10a
stand for
bifurcated, continuous, low frequency, low frequency and
mirror,
and mirror mode spectra, respectively, as described above
in reference to Figure 9.
Anderson et al. [1994]
used a collection of 102 magnetosheath
intervals observed by the AMPTE/CCE spacecraft and sorted the
observed spectra into these types.
The letters ("B,'' "C'' etc.) in Figure 10a are
placed at a value of
b||p corresponding to the
average value of
observed
b||p for each spectral
type.
The structure of the wave spectra displayed in Figure 9
was accounted for by
Denton et al. [1994c].
Their work
was based on a simple model of the magnetosheath which assumed
4% He2+ and incorporated the anisotropy-beta relation
(4); a Vlasov dispersion solver was used to solve for
the real and imaginary parts of the wave frequency. Figure 10
shows the main results of their model. Figure 10a
shows
that the ion cyclotron instability splits into two branches at low
parallel beta
b||p, one driven by the
temperature anisotropy of the
protons (marked "p'') and one driven by the temperature
anisotropy of the He2+ (alpha particles) (marked "
a '').
These two modes merge at high
b||p.
Figure 10b
shows the normalized growth rate for these two
modes and also for the mirror mode (which has zero real frequency, so
it does not appear in Figure 10a).
The letters "B,'' "C,'' "L,'' "LM,'' and "M'' in
Figure 10a
stand for
bifurcated, continuous, low frequency, low frequency and
mirror,
and mirror mode spectra, respectively, as described above
in reference to Figure 9.
Anderson et al. [1994]
used a collection of 102 magnetosheath
intervals observed by the AMPTE/CCE spacecraft and sorted the
observed spectra into these types.
The letters ("B,'' "C'' etc.) in Figure 10a are
placed at a value of
b||p corresponding to the
average value of
observed
b||p for each spectral
type.
It is clear that
the theoretical curves in
Figure 10a
indicate bifurcated spectra (distinct proton and
alpha particle branches), continuous spectra (with frequency extending
above
wr / Wp
= 0.25 ), and low frequency
( wr / Wp
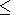 0.25 ) spectra at the
respective
b||p values indicated by
the letters
"B,'' "C,'' and
"L'' and "LM.''
Furthermore, the growth rate of the mirror mode
becomes comparable than that of the ion cyclotron waves at a value of
b||p corresponding to the
"LM'' (low frequency and mirror) spectra,
and becomes greater than that
of the ion cyclotron waves at a value of
b||p corresponding to the
"M'' (mirror) spectra,
Note the remarkable similarity between the frequency spread of
transverse power in Figure 9 and the spread of ion
cyclotron real frequency in Figure 10. Based on the
detailed agreement between the observations and model, we
regard the identification of these ion cyclotron and mirror
waves as quite solid.
0.25 ) spectra at the
respective
b||p values indicated by
the letters
"B,'' "C,'' and
"L'' and "LM.''
Furthermore, the growth rate of the mirror mode
becomes comparable than that of the ion cyclotron waves at a value of
b||p corresponding to the
"LM'' (low frequency and mirror) spectra,
and becomes greater than that
of the ion cyclotron waves at a value of
b||p corresponding to the
"M'' (mirror) spectra,
Note the remarkable similarity between the frequency spread of
transverse power in Figure 9 and the spread of ion
cyclotron real frequency in Figure 10. Based on the
detailed agreement between the observations and model, we
regard the identification of these ion cyclotron and mirror
waves as quite solid.
5.5. Magnetopause Current Layer
Broadband transverse waves are observed in the magnetopause current
layer (region
of large magnetic shear), especially during periods of
southward IMF leading to large magnetic shear at the
magnetopause
[Rezeau et al., 1989, 1993;
Song et al., 1993];
see also [Anderson and Fuselier, 1993].
All of these authors assume that the broadband waves are
associated with reconnection.
Rezeau et al. [1989]
describe the
waves as Alfvénic, while Song et al.
[1993]
describe the
waves with peak power as ion cyclotron waves.
Song et al. [1993]
states also that the wave power extends up to the electron
gyrofrequency. This high frequency turbulence is also highly
correlated with the magnetic shear
[Zhu et al., 1996]
and is
now thought to be associated with whistler waves resulting from
reconnection
[Mandt et al., 1994;
Shay et al., 1999].
Johnson and Cheng [1997]
describe these waves as kinetic
Alfvén waves resulting from mode conversion
of compressional (mirror)
modes convecting toward the magnetopause. The mode conversion
occurs in the region of magnetic shear due to finite Larmour radius
effects. They argue that particle transport resulting from these
waves can be quite substantial. While there are appealing features
to this theory, it seems to us that more work needs to be done to
verify observationally that such mode conversion is actually
occurring (some recent progress in this direction has been made
[Park et al., 1999]).
6. Summary
There are four basic ultra-low-frequency (ULF) modes, the
Alfvén/ion cyclotron mode, the
magnetosonic/fast/whistler mode,
the ion acoustic/slow/sound mode, and the mirror mode
(Section 2).
These can in principle be identified with the help of transport ratios,
phase relationships, and polarization information. In many
cases, however, a unique identification is difficult to make.
Problems are that the theories are usually based on the linear
homogeneous assumption, and that there may be a superposition
of observed modes.
Whether the upstream conditions are quasi-parallel or
quasi-perpendicular depends on the orientation of the
interplanetary magnetic field (IMF) at the bowshock (quasi-parallel
indicates that the IMF is roughly parallel to the shock normal;
see Section 3). When the upstream conditions are
quasi-parallel, the magnetosheath plasma usually has a large value of
beta, and is characterized by a broad band turbulent
spectrum of waves with little ordering by the ill-defined
(for high beta) ambient magnetic field (Section 4).
The observed wave power is
generally thought to be transmitted, with some modification, through
the magnetosheath to the magnetosphere from the foreshock.
When the upstream conditions are
quasi-perpendicular, the dominant waves
(Section 5) appear to be caused by
temperature anisotropy ( T p > T|
p ), which is in turn
initially caused by
reflection at the bowshock and then driven by the compression
and stretching of convecting flux tubes. In the middle magnetosheath,
the mirror mode is usually the dominant mode. There can also be
ion cyclotron waves, especially near the bowshock and
in the plasma depletion layer (if there is one) near the magnetopause.
Mirror modes observed near the magnetopause develop a finite upstream
phase velocity as they are unable to penetrate the low beta
magnetospheric plasma. Broadband Alfvénic
waves are observed
in the magnetopause current layer which are associated with
reconnection or possibly with kinetic Alfvén
waves.
p > T|
p ), which is in turn
initially caused by
reflection at the bowshock and then driven by the compression
and stretching of convecting flux tubes. In the middle magnetosheath,
the mirror mode is usually the dominant mode. There can also be
ion cyclotron waves, especially near the bowshock and
in the plasma depletion layer (if there is one) near the magnetopause.
Mirror modes observed near the magnetopause develop a finite upstream
phase velocity as they are unable to penetrate the low beta
magnetospheric plasma. Broadband Alfvénic
waves are observed
in the magnetopause current layer which are associated with
reconnection or possibly with kinetic Alfvén
waves.
Inhomogeneity plays a crucial role in the generation and evolution
of all these waves. For instance, temperature anisotropy
(which drives the ion cyclotron and mirror waves)
is caused by the presence of the bowshock and the compression and
lengthening of flux tubes as they convect across the magnetosheath.
Further examples are the modification of the
mirror mode near the magnetopause due to the
decreasing beta and the generation of waves in the magnetopause
current layer due to large magnetic shear. In the quasi-parallel
magnetosheath, the broad-band turbulence is in part generated
by foreshock waves which come about due to the presence of the
bowshock.
The waves also appear to have an appreciable feedback to the
macroscopic
plasma. The most certain effect we know about is the regulation
of the temperature ratio
T p/T|
p by ion cyclotron waves.
The energy exchange caused by the waves (from
T
p/T|
p by ion cyclotron waves.
The energy exchange caused by the waves (from
T p to
T||p )
has an important effect on the
evolution of the separate
T
p to
T||p )
has an important effect on the
evolution of the separate
T p and
T||p.
Based on the
effect of the waves, an anisotropic ( T
p and
T||p.
Based on the
effect of the waves, an anisotropic ( T p
p 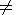 T||p )
fluid
model has been developed which appears to do a good job of
describing the temperature evolution in the magnetosheath
[Denton et al., 1994c, 1995b],
and this model has been used
in fluid simulations of the magnetosheath
[Denton and Lyon, 1996].
Whether the whistler waves observed
in the reconnection region are a cause or an effect is still under
study, but it is clear now that the whistler dynamics which gives
rise to the waves plays a crucial role in fast collisionless
reconnection
[Shay et al., 1999].
Possibly
mode conversion of compressional (mirror) waves to kinetic Alfvén
waves leads to enhanced transport of
particles across the magnetopause
[Johnson and Cheng, 1997].
T||p )
fluid
model has been developed which appears to do a good job of
describing the temperature evolution in the magnetosheath
[Denton et al., 1994c, 1995b],
and this model has been used
in fluid simulations of the magnetosheath
[Denton and Lyon, 1996].
Whether the whistler waves observed
in the reconnection region are a cause or an effect is still under
study, but it is clear now that the whistler dynamics which gives
rise to the waves plays a crucial role in fast collisionless
reconnection
[Shay et al., 1999].
Possibly
mode conversion of compressional (mirror) waves to kinetic Alfvén
waves leads to enhanced transport of
particles across the magnetopause
[Johnson and Cheng, 1997].
Acknowledgments
We gratefully acknowledge helpful conversations with
Mark Engebretson, Steven Schwartz, and Brian Anderson.
This work was supported by NSF (ATM-9622071) and
by NASA (NAG 5-1098).
References
Anderson, B. J.,
Statistical studies of Pc3-5 pulsations and their relevance
for possible source mechanisms of ULF waves,
Ann. Geophys., 11, 128, 1993.
Anderson, B. J., and S. A. Fuselier,
Magnetic pulsations from 0.1 to 4.0 Hz
and associated plasma properties
in the Earth's subsolar magnetosheath and plasma depletion layer,
J. Geophys. Res., 98, 1461, 1993.
Anderson, B. J., S. A. Fuselier, S. P. Gary, and R. E. Denton,
Magnetic spectral signatures in the Earth's
magnetosheath and plasma depletion layer,
J. Geophys. Res., 99, 5877, 1994.
Blanco-Cano, X., and S. J. Schwartz,
Identification of low-frequency kinetic wave modes in the Earth's
ion foreshock,
Ann. Geophysicae, 15, 273, 1997.
Brinca, A. L., N. Sckopke, and G. Paschmann,
Wave excitation downstream of the low-
b quasi-perpendicular
bow shock,
J. Geophys. Res., 95, 6331, 1990.
Chew, G. F., M. L. Goldberger, and F. E. Low,
The Boltzmann equation and the one-fluid hydromagnetic equations
in the absence of particle collisions,
Proc. R. Soc. London, Ser. A., 236, 112, 1956.
Denton, R. E.,
ULF Waves in the Magnetosheath,
IUGG Birmingham 19-30 July 1999 Abstracts Book A, A.340, 1999.
Denton, R. E., and J. G. Lyon,
Density depletion in an anisotropic magnetosheath,
J. Geophys. Res., 23, 2891, 1996.
Denton, R. E., M. K. Hudson, S. A. Fuselier, and B. J. Anderson,
Electromagnetic ion cyclotron waves in the plasma depletion layer,
J. Geophys. Res., 98, 13,477, 1993.
Denton, R. E., S. P. Gary, B. J. Anderson, S. A. Fuselier,
and
M. K. Hudson,
Low-frequency magnetic fluctuation spectra in the magnetosheath
and plasma depletion layer,
J. Geophys. Res., 99, 5893, 1994a.
Denton, R. E., B. A. Anderson, S. A. Fuselier, S. P. Gary,
and
M. K. Hudson,
Ion anisotropy driven waves in the Earth's
magnetosheath and plasma depletion layer,
in AGU Monograph 84, Solar System Plasmas in Space and Time,
edited by J. L. Burch and J. H. Waite, Jr.,
pp. 111-119, American Geophysical Union, Washington, D.C., 1994b.
Denton, R. E., B. J. Anderson, S. P. Gary, and S. A. Fuselier,
Bounded anisotropy fluid model for ion temperatures,
J. Geophys. Res., 99, 11,225, 1994c.
Denton, R. E., S. P. Gary, X. Li, B. J. Anderson, J. W. LaBelle,
and M. Lessard,
Low-frequency fluctuations in the magnetosheath near the
magnetopause,
J. Geophys. Res, 100, 5665, 1995a.
Denton, R. E., X. Li, and T-D. Phan,
Bounded anisotropy fluid model for ion temperature
evolution applied to AMPTE/IRM magnetosheath data,
J. Geophys. Res, 100, 14,925, 1995b.
Denton, R. E., B. J. Anderson, G. Ho, and D. C. Hamilton,
Effects of wave superposition on the polarization of
electromagnetic ion cyclotron waves,
J. Geophys. Res., 101, 24,869, 1996.
Denton, R. E., M. R. Lessard, J. W. LaBelle, and S. P. Gary,
Identification of low-frequency magnetosheath waves,
J. Geophys. Res., 103, 23,661, 1998.
Engebretson, M. J., N. Lin, W. Baumjohann, H. Luehr, B. J. Anderson,
L. J. Zanetti, T. A. Potemra, R. L. McPherron, and
M. G. Kivelson,
A comparison of ULF fluctuations in the solar wind,
magnetosheath, and dayside magnetosphere,
J. Geophys. Res., 96, 3441, 1991.
Engebretson, M. J., K. Takahashi, and M. Scholer (Eds.),
in AGU Monograph 81, Solar Wind Sources of Magnetospheric Ultra-Low-Frequency
Waves,
424 pp., American Geophysical Union, Washington, D.C., 1994.
Fairfield, D. H.,
Waves in the vicinity of the magnetopause,
in
Magnetospheric Particles and Fields,
edited by
B. M. McCormac,
pp. 67-77, D. Reidel, Hingham, Mass., 1976.
Fazakerley, A. N., and D. J. Southwood,
Theory and observation of magnetosheath waves,
in AGU Monograph 81, Solar Wind Sources of Magnetospheric Ultra-Low-Frequency
Waves,
edited by M. J. Engebretson, K. Takahashi, and M. Scholer,
pp. 147-158, American Geophysical Union, Washington, D.C., 1994.
Fuselier, S. A., D. M. Klumpar, and E. G. Shelley,
On the origins of energetic ions in the Earth's dayside magnetosheath,
J. Geophys. Res., 96, 47, 1991.
Fuselier, S. A., B. A. Anderson, S. P. Gary, and R. E. Denton,
Ion anisotropy/beta correlations in the Earth's quasi-parallel
magnetosheath,
J. Geophys. Res., 99, 14,931, 1994.
Gary, S. P.,
Theory of space plasma microinstabilities,
181 pp.,
University of Cambridge, New York, 1993.
Gary, S. P., and D. Winske,
Correlation function ratios and the identification of space plasma
instabilities,
J. Geophys. Res., 97, 3103, 1992.
Gary, S. P., S. A. Fuselier, and B. J. Anderson,
Ion anisotropy instabilities in the magnetosheath,
J. Geophys. Res., 98, 1481, 1993.
Gary, S. P., B. J. Anderson, R. E. Denton, S. A. Fuselier,
and M. E. McKean,
A closure relation for anisotropic plasmas from the
Earth's magnetosheath,
Phys. of Plasmas, 1, 1676, 1994.
Hubert, D.,
Nature and origin of wave modes in the dayside Earth magnetosheath,
Adv. Space Res., 14 (7), 55, 1994.
Hubert, D., C. Perche, C. C. Harvey, C. Lacombe, and C. T. Russell,
Observation of mirror waves downstream of a quasi-perpendicular
shock,
Geophys. Res. Lett., 16, 159, 1989.
Johnson, J. R., and C. Z. Cheng,
Global structure of mirror modes in the magnetosheath,
J. Geophys. Res., 102, 7179, 1997.
Kennel, C. F. and H. E. Petschek, Limit on stable trapped particle
fluxes,
J. Geophys. Res., 71, 1, 1966.
Krauss-Varban, D.,
Bow shock and magnetosheath simulations: wave transport and
kinetic properties,
in AGU Monograph 81, Solar Wind Sources of Magnetospheric Ultra-Low-Frequency
Waves,
edited by M. J. Engebretson, K. Takahashi, and M. Scholer,
pp. 121-134, American Geophysical Union, Washington, D.C., 1994.
Krauss-Varban, D., N. Omidi, and K. B. Quest,
Mode properties of low-frequency waves: Kinetic theory
versus Hall-MHD,
J. Geophys. Res., 99, 5987, 1994.
Lacombe, C., F. G. E. Pantellini, D. Hubert, C. C. Harvey, A. Mangeney,
G. Belmont, and C. T. Russell,
Mirror and Alfvénic waves observed by
ISEE 1-2 during crossings
of the Earth's bow shock,
Ann. Geophysicae, 10, 772, 1992.
Lacombe, C., G. Belmont, D. Hubert, C. C. Harvey, A. Mangeney,
C. T. Russell, J. T. Gosling, and S. A. Fuselier,
Density and magnetic field fluctuations observed by ISEE 1-2 in the
quiet magnetosheath,
Ann. Geophysicae, 13, 343, 1995.
Lin, C.-H., J. K. Chao, L. C. Lee, D. J. Wu, Y. Li, B. H. Wu,
and P. Song,
Identification of mirror waves by the phase difference between
perturbed magnetic field and plasmas,
J. Geophys. Res., 103, 6621, 1998.
Mandt, M. E., R. E. Denton, and J. F. Drake,
Transition to Whistler Mediated Magnetic Reconnection,
J. Geophys. Res., 21, 73, 1994.
McKean, M. E., D. Winske, and S. P. Gary,
Mirror and ion cyclotron anisotropy instabilities in the
magnetosheath,
J. Geophys. Res., 97, 19,421, 1992.
McKean, M. E., D. Winske, and S. P. Gary,
Two-dimensional simulations of ion anisotropy instabilities in
the magnetosheath,
J. Geophys. Res., 99, 11,141, 1994.
Omidi, N., and D. Winske,
Structure of the magnetopause inferred from one-dimensional
hybrid simulations,
J. Geophys. Res., 100, 11,935, 1995.
Park, W., J. R. Johnson, and C. Z. Cheng,
Comparison of low-frequency MHD waves at the magnetopause
with magnetic shear - A signature of mode conversion,
EOS Trans. AGU, 80 (46), Fall Meet. Suppl., F902, 1999.
Phan, T. D.,
G. Paschmann, W. Baumjohann, N. Sckopke,
and H. Lühr,
The magnetosheath region adjacent to the dayside magnetopause:
AMPTE/IRM observations,
J. Geophys. Res., 99, 121, 1994.
Rezeau, L., A. Morane, S. Perraut, and A. Roux,
Characterization of Alfvénic fluctuations
in the
magnetopause boundary layer,
J. Geophys. Res., 94, 101, 1989.
Rezeau, L., A. Roux, and C. T. Russell,
Characterization of small-scale structures at the magnetopause
from ISEE measurements,
J. Geophys. Res., 98, 179, 1993.
Russell, C. T., J. G. Luhmann, R. C. Elphic, D. J. Southwood,
M. F. Smith,
and A. D. Johnstone,
Upstream waves simultaneously observed by ISEE and UKS,
J. Geophys. Res., 92, 7354, 1987.
Schwartz, S. J., D. Burgess, and J. J. Moses,
Low-frequency waves in the Earth's magnetosheath: Present status,
Ann. Geophys., 14, 1134, 1996.
Sckopke, N., G. Paschmann, A. L. Brinca, C. W. Carlson, and H. Lühr,
Ion thermalization in quasi-perpendicular shocks involving reflected
ions,
J. Geophys. Res., 95, 6337, 1990.
Shay, M. A., J. F. Drake, B. Rogers and R. E. Denton,
The GEM Reconnection Challenge: the
role of whistler physics in particle, hybrid and Hall MHD simulations,
J. Geophys. Res., submitted, 1999.
Song, P., and C. T. Russell,
What do we really know about the magnetosheath,
Adv. Space Res., 20 (4), 747, 1997.
Song, P., R. C. Elphic, C. T. Russell, J. T. Gosling, and C. A. Cattell,
Structure and properties of the subsolar magnetopause for northward
IMF: ISEE observations,
J. Geophys. Res., 95, 6375, 1990a.
Song, P., C. T. Russell, J. T. Gosling, M. F. Thomsen, and R. C. Elphic,
Observations of the density profile in the magnetosheath near
the stagnation streamline,
Geophys. Res. Lett., 17, 2035, 1990b.
Song, P., C. T. Russell, and M. F. Thomsen,
Slow mode transition in the frontside magnetosheath,
J. Geophys. Res., 97, 8295, 1992a.
Song, P., C. T. Russell, and M. F. Thomsen,
Waves in the inner magnetosheath: A case study,
Geophys. Res. Lett., 19, 2191, 1992b.
Song, P., C. T. Russell, and C. Y. Huang,
Wave properties near the subsolar magnetopause:
Pc1 waves in the sheath transition layer,
J. Geophys. Res., 98, 5907, 1993.
Song, P., C. T. Russell, and S. P. Gary,
Identification of low-frequency fluctuations in the terrestrial
magnetosheath,
J. Geophys. Res., 99, 6011, 1994.
Song, P., C. T. Russell, and L. Chen,
On large amplitude MHD waves in high beta plasma,
J. Geophys. Res., 103, 29,569, 1998.
Tsurutani, B. T., E. J. Smith, R. R. Anderson, K. W. Ogilvie,
J. D. Scudder, D. N. Baker, and S. J. Bame,
Lion roars and nonoscillatory drift mirror waves in the magnetosheath,
J. Geophys. Res., 87, 6060, 1982.
Zhu, Z., P. Song, J. F. Drake, C. T. Russell, R. R. Anderson,
D. A. Gurnett, K. W. Ogilvie, and R. J. Fitzenreiter,
The relationship between ELF-VLF waves and magnetic shear at
the dayside magnetopause,
Geophys. Res. Lett., 23, 773, 1996.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.2.0) on August 3, 2000.
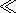 Fcp, where
Fcp is the
proton cyclotron
frequency, up to four distinct modes can propagate in a relatively
isotropic plasma: the three waves corresponding to the normal
modes of MHD theory and the mirror mode. The mirror mode has
zero phase velocity in a homogeneous plasma (though it can acquire
a finite phase velocity when there is inhomogeneity
[Johnson and Cheng, 1997]).
The three modes with finite phase velocity are the
magnetosonic/fast/whistler mode, the
Alfvén/ion-cyclotron mode,
and the ion-acoustic/slow/sound mode.
The first term listed
(i.e., "magnetosonic,'' "Alfvén,'' and
"ion acoustic'')
represents our preferred notation
[Denton et al., 1995a]
and the
other terms have been used by other authors
[for example,
Krauss-Varban et al., 1994].
The terms "fast'' and "slow'' here are
appropriate descriptions of
the phase speed of the respective waves at low
parallel beta
b||p
Fcp, where
Fcp is the
proton cyclotron
frequency, up to four distinct modes can propagate in a relatively
isotropic plasma: the three waves corresponding to the normal
modes of MHD theory and the mirror mode. The mirror mode has
zero phase velocity in a homogeneous plasma (though it can acquire
a finite phase velocity when there is inhomogeneity
[Johnson and Cheng, 1997]).
The three modes with finite phase velocity are the
magnetosonic/fast/whistler mode, the
Alfvén/ion-cyclotron mode,
and the ion-acoustic/slow/sound mode.
The first term listed
(i.e., "magnetosonic,'' "Alfvén,'' and
"ion acoustic'')
represents our preferred notation
[Denton et al., 1995a]
and the
other terms have been used by other authors
[for example,
Krauss-Varban et al., 1994].
The terms "fast'' and "slow'' here are
appropriate descriptions of
the phase speed of the respective waves at low
parallel beta
b||p  8 pp||p/B02
in CGS units, where
p||p is the proton pressure parallel to
B,
and
B is the magnetic field.
At high beta, what we call the "slow'' mode sometimes has the
largest phase
velocity
[Denton et al., 1995a;
Krauss-Varban et al., 1994].
Our use of the terms "slow'' and "fast'' here agrees with
the nomenclature of
Krauss-Varban et al. [1994],
which was
designed to use the same term to refer to the wave with similar
fluctuations (transport ratios),
regardless of phase speed. On the other hand,
Gary and Winske [1992]
and
Lacombe et al. [1992, 1995]
have retained the use of "slow'' and "fast'' to refer explicitly
to phase speed. (It is easy to see why we would prefer not to
use these terms.)
8 pp||p/B02
in CGS units, where
p||p is the proton pressure parallel to
B,
and
B is the magnetic field.
At high beta, what we call the "slow'' mode sometimes has the
largest phase
velocity
[Denton et al., 1995a;
Krauss-Varban et al., 1994].
Our use of the terms "slow'' and "fast'' here agrees with
the nomenclature of
Krauss-Varban et al. [1994],
which was
designed to use the same term to refer to the wave with similar
fluctuations (transport ratios),
regardless of phase speed. On the other hand,
Gary and Winske [1992]
and
Lacombe et al. [1992, 1995]
have retained the use of "slow'' and "fast'' to refer explicitly
to phase speed. (It is easy to see why we would prefer not to
use these terms.)


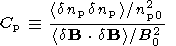
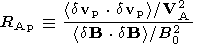
 k ) and properties
of the cross-helicity
which enabled them to eliminate the sign ambiguity (
k ) and properties
of the cross-helicity
which enabled them to eliminate the sign ambiguity ( 

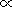 A-1 and
T||p
A-1 and
T||p 
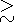 10 represent
quasi-parallel upstream conditions. Another diagnostic for
quasi-parallel upstream conditions is the presence of elevated
fluxes of energetic He2+ [Fuselier et al.,
10 represent
quasi-parallel upstream conditions. Another diagnostic for
quasi-parallel upstream conditions is the presence of elevated
fluxes of energetic He2+ [Fuselier et al., 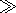 T||p develops
just downstream of the bowshock
[Sckopke et al.,
T||p develops
just downstream of the bowshock
[Sckopke et al., 
 B )
propagation to
nearly linearly polarized for highly oblique waves
[Denton et al,
B )
propagation to
nearly linearly polarized for highly oblique waves
[Denton et al, 
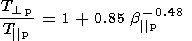





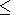 0.25 ) spectra at the
respective
b||p values indicated by
the letters
"B,'' "C,'' and
"L'' and "LM.''
0.25 ) spectra at the
respective
b||p values indicated by
the letters
"B,'' "C,'' and
"L'' and "LM.''
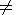 T||p )
fluid
model has been developed which appears to do a good job of
describing the temperature evolution in the magnetosheath
[Denton et al.,
T||p )
fluid
model has been developed which appears to do a good job of
describing the temperature evolution in the magnetosheath
[Denton et al.,