A. D. Danilov
Institute of Applied Geophysics, Moscow, Russia
A. V. Mikhailov
Institute of Terrestrial Magnetism, Ionosphere, and Radio Wave Propagation, Troitsk, Moscow Region, Russia
The problem of long-term variations (trends) in parameters of the upper atmosphere and ionosphere currently attracts attention (see the reviews by Danilov [1997] and Danilov and Smirnova [1997]).
The results of ionospheric measurements should play a leading role in the analysis of long-term changes in the upper atmosphere. The first indication of a presence of trends in the upper atmosphere parameters was obtained merely on the basis of observations of radio wave absorption in the D region [Bremer, 1992; Nestorov et al., 1991; Taubenheim et al., 1990].
The most frequently used ionospheric parameter is the F2 layer critical frequency foF2. There are long enough series of foF2 observations at several ionospheric stations all over the globe, and some attempts have been made during recent years to reveal foF2 long-term trends [Bremer, 1996; Danilov and Mikhailov, 1998a, 1998b; Givishvili and Leshchenko, 1993, 1994, 1995].
Danilov and Mikhailov [1998a, 1998b] proposed a principally new approach to derivation of foF2 trends. In this paper we further develop this approach, show that it leads to principally new results (disappearance of the seasonal effect in the trends and increase in its absolute values), and illustrate it by the data of several ionospheric stations.
The first step in developing a new approach for looking at foF2 trends was to use relative values of the critical frequency instead of the absolute values used by Bremer [1996] and Givishvili and Leshchenko [1993, 1994, 1995]. Danilov and Mikhailov [1998a] proposed to look for trends not in the absolute values of foF2 but in the relative deviations of the observed values from some mean (that is, constructed without any allowance for long-term trends) model:
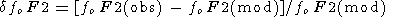| (1) |
This approach was used slightly earlier by Danilov and Smirnova [1997] in looking for trends in the E region ion composition on the basis of rocket mass spectrometer measurements.
The principal advantage of the method suggested is the following. Analyzing absolute values of foF2, one cannot use jointly the data for various LT moments and months, because there exist strong diurnal and seasonal variations of this parameter. If the deviations of observed foF2 values from some mean model (created without any allowance for possible long-term trends) are used, one is able to analyze jointly all the data available, because the absolute values are insignificant and only variations of the foF2 deviations during several decades are sought. Evidently, if any trend does exist, deviations of one sign (relative to the mean model) in earlier years and of the opposite sign in later years should be seen.
The regression of the critical frequencies with respect to the 12-month running mean values of the sunspot number R approximated by the third power polynomial was used as a model.
Analyzing the foF2 data, Danilov and Mikhailov [1998a] directly used the foF2 monthly medians. A pronounced negative trend was derived in Moscow at the daytime hours for January, February, May, June, July, August, and September, but the trend for other months was close to zero or even positive. In fact, this conclusion on different foF2 trends in various months was similar to that obtained by Bremer [1996] and Givishvili and Leshchenko [1993, 1994, 1995].
Later Danilov and Mikhailov [1998b] proposed using for the analysis not the initial monthly mean values, but smoothed 12-month running mean values of foF2. Since the 12-month running mean sunspot number R12 is used in the above mentioned regressions of foF2, it seems reasonable to use also smoothed values of the critical frequencies as foF2 (obs) in (1). The use of smoothed foF2 reduces the scatter of individual points around the regression curve.
The next step in the development of a new approach to look for foF2 trends was the following. The reliability of the dfoF2 values obtained in the analysis depends to a great degree on the reliability of the model used, that is, on the reliability of the foF2 regression with respect to R12. It is widely known that there is a so-called "hysteresis" effect in the solar cycle foF2 variations. The effect is seen at the rising and falling phases of a solar cycle and, roughly speaking, is manifested in different values of foF2 (under identical other conditions) under the same value of R12. The effect may create significant noise in the model and distort the resulting dfoF2 values.
Danilov and Mikhailov [1998b] attempted to analyze only the data for 5 years around the solar activity minima and found that the negative trends for Moscow became better pronounced for all seasons if such reduced data were used.
However, 5 years cover too long a period, and so parts of the falling and rising phases of the solar cycle may again be involved in the analysis. On the other hand, one should not expect a manifestation of the hysteresis effect also around solar maxima. That is why we finally propose, looking for foF2 trends, to use three years around each maximum and minimum (1946-1948, 1953-1955, 1957-1959, 1963-1965, 1967-1969, 1975-1977, 1978-1980, 1985-1990, and 1995-1997). One can easily see that mainly the years of long enough falling phases (for example, 1970-1974) are excluded from the analysis. It appeared that such a reduction of the data leads to fundamental changes of conclusions on the foF2 trends.
Below we will consider in detail the results for the Moscow station to compare them with previous results and to demonstrate the effects of a new approach application and then summarize the results for other ionospheric stations.
We discuss here the data of the Moscow ionospheric station and, first, demonstrate the effects of new approach application to the data for 1200 LT and March.
Figure 1 shows the
dfoF2 values versus
time for all the years
available (1946-1996). A weak positive trend
( +1.8 
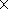10-4
per
year; see Table 1)
is visually seen. It should be noted that
if one limits the analysis by 1990-1991 (that is exactly what has
been done by
Givishvili and Leshchenko [1993, 1994,
1995]
and
Danilov and Mikhailov [1998a, 1998b]),
one gets a weak negative trend for these data. The reversal of the
trend sign, when the data until 1996 are added, occurs mainly
because of the 1991-1994 points which correspond to the falling
phase of solar activity (see above).
Figure 2 shows the same data for the same period but with only
the
years around solar maxima M(3) and minima m(3)
left. The change of
the situation is dramatic. Now there is a well-pronounced negative
trend ( k = -6.7 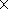10-4).
Analyzing the data for Moscow, Givishvili and Leshchenko [1993, 1994, 1995] and Danilov and Mikhailov [1998a] obtained different values of the trend (and even different sign of it) for different months. However, it seems doubtful that the long-term changes in foF2 during several decades would have a pronounced seasonal behavior. In the scope of current ideas one would rather expect that the foF2 trends manifest some systematic and single-directed changes of the entire upper atmosphere (for example, a cooling, variations of transport process, etc.), which should not depend on relatively short-term seasonal variations. There is a danger that the seasonal effect in the trends derived is due either to inhomogeneity of the initial data distribution over seasons or to the method of trend derivation itself.
Table 1 shows the slope
k of the linear approximation of the
dfoF2 data plotted
versus time for four months (representing all
seasons). Actually,
k gives a relative change in
foF2 per year. It
is evident from the third column of Table 1 that, with the new
approach proposed, one obtains negative trends of the same sign
(negative) and nearly the same magnitude (about
-6 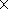10-4)
for all
seasons.
To illustrate the advantages of the new approach, the bottom line in Table 1 shows the foF2 trends for winter. The principal results do not significantly differ from those for individual months, but in this case every point is a result of averaging over three winter months; so its statistical provision is, roughly speaking, 3 times higher.
We checked our conclusions drawn for 1200 LT, using the data for other LT moments (1000 LT and 1400 LT), and obtained the same results. Actually, the method suggested makes it possible to use jointly all months and all LT moments to increase statistical provision of the results.
It is worth looking for possible changes with time of the trend magnitude. The last two columns of Table 1 show the foF2 trends for the period since 1965 only. Again, if the data for all years are used, there is a contradiction even in sign between various months, but the trend is negative and of the same magnitude if only the M(3) and m(3) years are used.
An important feature of Table 1 is that the values of the trends since 1965 are about twice as high as those of the trends since 1946. This effect is even stronger for some other stations (for example, St. Petersburg). This fact may mean that the foF2 depletion during the three recent decades occurs more rapidly than during the preceding decades. The fact may be important while looking for the causes of the trends described.
The method in question provides values of relative changes
in
foF2.
For example, the last column in Table 1 shows that since 1965
foF2 decreases, on the average, by 0.1% per year.
To compare this value
with the results of the absolute value analysis, we take the mean
value of
foF2 to be equal to 8.2 MHz. Then the
foF2 trend derived
is
8.2 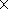10-3 MHz per year. This
value for the Moscow station is
higher than the value of
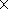3 10-3 MHz per year given by
Givishvili and Leshchenko [1993]
and
Danilov and Mikhailov [1998a, 1998b].
This may be due to the more
sophisticated method used to look for
foF2 trends in this paper as
compared to the method used in the above indicated papers.
The same procedure as described in the previous section was applied to the data of four other stations: St. Petersburg, Alma-Ata, Rugen, and Sodankyla. The results are shown in Table 2.
One can see from Table 2, that the principal picture for all stations is practically the same as described above for Moscow. Inclusion into the analysis of all the years leads to small positive or close to zero trends. Reduction of the data to only the M(3) and m(3) years gives a stable negative trend with close magnitudes for different months. Further reduction of the data (only since 1965) leads to a further increase of the negative values of k. In the case of the St. Petersburg station this reduction increases the magnitude of the negative trend by several times.
It is worth emphasizing that for all the stations considered the scatter of the k values in the case of all years used (the second column) is very strong (up to 5 times), and in some cases there is even a sign reversal, whereas for the M (3)+ m(3) reduction of the data, the difference in k for various months is, as a rule, relatively small (tenths of percents). We believe that this fact may be considered as some additional argument in favor of the new approach described.
It has
already
been
mentioned above that low values of the
foF2 trends had been obtained
by
Bremer [1996],
who used all the
years. This fact agrees well with the second column of Table 2. The
third column demonstrates that use of the data for the M(3) and
m(3) years only leads to negative trends of nearly the same
magnitude as for the Moscow and St. Petersburg stations. As an
example, Figure 3
shows the
dfoF2 variations
for Rugen for
July.
Comparison of the trends derived for all five stations
considered (Tables 1 and 2) indicates the presence of some
latitudinal variation of the trends. The least pronounced trends
are derived for the low-latitude Alma-Ata station ( k is about
-3 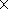10-4 for the M
(3)+ m(3) years after 1965).
The signal is low, and
so the effects well seen at other stations are not so visually
pronounced on the noisy background.
The highest trends ( k 
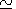50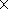
10-4) are obtained for the
high-latitude Sodankyla station (see Figure 4 for illustration).
For this station, negative trends are seen even if all the years are
used. That agrees with well-pronounced trends obtained for this
station by
Danilov and Mikhailov [1998b].
And,
nevertheless, reduction of the data in the scope of the new
approach increases the trend magnitude by more than 2 times. The
midlatitude stations Rugen, Moscow, and St. Petersburg demonstrate
close values of the trends ( k = (1-2) 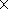10-4), which lie
between
the corresponding values for Sodankyla and Alma-Ata.
Five stations are not enough to derive solid conclusions on latitudinal effects in the trends, but we may state, at least, that there are some indications for the presence of such effects.
A new method for analyzing the long-term
foF2 trends is proposed. The
principal point of the method is to use relative rather than
absolute
foF2 variations and consider only the periods around
solar
maxima and minima in the cycles to avoid the distortion of the
foF2 values by the hysteresis effect at the rising
and falling phases of
a solar cycle. The vertical sounding data for the Moscow, Rugen,
St. Petersburg, and Sodankyla stations were analyzed with the help
of this method, and a pronounced negative trend for all months were
revealed. An averaged over all seasons negative trend in
foF2 for
Moscow was found to be
8.2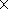 10-3 MHz yr
-1.
This value is 2-2.5 times higher than that obtained earlier by
Givishvili and Leshchenko [1993, 1994,
1995]
and
Danilov and Mikhailov [1998a, 1998b].
Using the new method, in which relative (with respect to some empirical model created without any allowance for trends) foF2 variations are considered, one can increase the statistical provision of the conclusions, because it becomes possible to consider jointly the data for different local times and seasons. If only the years in the vicinity of solar activity minima and maxima are considered (to reduce the influence of distorting effects, for example, that of hysteresis), stable negative trends are derived for all stations considered.
Some indications are obtained that there is a latitudinal effect in the foF2 trends (higher values at higher latitudes) and that the trends for the two recent decades may be higher than the average ones derived for the entire period of observations.
Bremer, J., Ionospheric trends in mid-latitudes as a possible indicator of the atmospheric greenhouse effect, J. Atmos. Terr. Phys., 54, 1505, 1992.
Bremer, J., Some additional results of long-term trends in vertical incidence data, paper presented at the COST 251 Meeting, Prague, Sept. 1996.
Danilov, A. D., Long-term variations of the temperature and composition of the mesosphere and lower thermosphere, Geomagn. Aeron., 37 (2), 1, 1997.
Danilov, A. D., and A. V. Mikhailov, Trends in the critical frequencies of the F2 region for the Moscow station, Geomagn. Aeron., 38 (1), 1998a.
Danilov, A. D., and A. V. Mikhailov, Long-term trends of the F2 -layer critical frequencies: A new approach, in Proceedings of the 2nd COST 251 Workshop "Algorithms and Models for COST 251 Final Product", 30-31 March 1998, Side, Turkey, p. 114, Rutherford Appleton Lab., U. K., 1998b.
Danilov, A. D., and N. V. Smirnova, Long-term trends of the ion composition in the E region, Geomagn. Aeron., 37, 35, 1997.
Givishvili, G. V., and L. N. Leshchenko, Long-term trends of the properties of the ionosphere and thermosphere at middle latitudes, Dokl. Ros. Akad. Nauk, 333 (1), 86, 1993.
Givishvili, G. V., and L. N. Leshchenko, Possible proofs of presence of a technogenic impact on the midlatitude ionosphere, Dokl. Ros. Akad. Nauk, 334 (2), 213, 1994.
Givishvili, G. V., and L. N. Leshchenko, Dynamics of the climatic trends in the midlatitude ionospheric E region, Geomagn. Aeron., 35 (3), 166, 1995.
Nestorov, G., D. Pancheva, and A. D. Danilov, Climatic changes in ionospheric absorption of radio waves in the SW range, Geomagn. Aeron., 31 (6), 1070, 1991.
Taubenheim, J., G. Cossart, and G. Entzian, Evidence of CO 2 induced progressive cooling of the middle atmosphere derived from radio wave observations, Adv. Space Res., 10 (10), 171, 1990.