Solar fluxes in the 10- to 30-nm range according to studies of the E region and the interlayer ionization valley

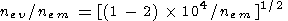
A. A. Nusinov, L. A. Antonova, and V. V. Katushina

Institute of Applied Geophysics, Moscow, Russia

Contents

Abstract

Introduction and Formulation of the Problem

Information on the absolute values, scales, and temporal characteristics of variations of the ultraviolet (UV) and X ray solar radiation are rather contradictory. In some spectral intervals, the uncertainty may exceed a factor of 2. This uncertainty is due to difficulties of measurements on board a satellite, low accuracy of the equipment, and short duration and irregularity of the measurements.

Owing to the absence of reliable data, in particular, there are no commonly accepted ideas on the spectral composition and absolute values of the solar radiation intensity in the important part of the extreme ultraviolet (EUV) range, 10-30 nm. Characteristics of the ionospheric thermal regime below 150 km, photoelectron spectrum parameters, and characteristics of the interlayer ionization valley are related to this spectral range.

Models available for calculation of the radiation in the wavelength range below 105 nm are based, primarily on the long-term measurements of the radiation spectra on board the Atmosphere Explorer-E (AE-E) satellite (see e.g. Hinteregger et al. [1991], Tobiska and Eparvier [1998], Siskind et al. [1995], Winningham et al. [1989] and Woods and Rottman [1990]). However, the 10- to 30-nm region appears to be the most complicated for both measurements and equipment calibration. For example, according to Richards and Torr [1984, 1985], the absolute calibration of the spectral devices of the AE-E satellite was conducted for wavelengths l above 25 nm, whereas at shorter wavelengths, either unreliable extrapolation of the calibration curves was applied, or (under l< 15 nm) some generalization of other, earlier, and not always reliable, measurements was used [Richards and Torr, 1984].

As a result, the aeronomical calculations, in which the AE-E satellite data of the EUV radiation (or the models based on these data) have been used, contradict the measurements of plasma parameters in the upper atmosphere. For example, on the basis of comparison of the energetic spectra of the photoelectons calculated with the EUV fluxes [Torr et al., 1979] and the energetic spectra measured on board the AE-C satellite, Richards and Torr [1984, 1985] draw the conclusion that the Torr et al. [1979] values of the EUV fluxes in the 10- to 25-nm range should be considered underestimated by about 2 times. As far as the data on EUV radiation in this region are important for aeronomy, it is reasonable to check and specify them on some independent material.

The alternate approach, not related to direct radiation measurements outside the atmosphere, is to study characteristics and variations of those atmospheric parameters which clearly manifest behavior of the EUV and X ray radiation. To do that, the E region of the daytime ionosphere may be successfully used, because its behavior is determined almost completely by variations of the ionizing radiation and is influenced relatively weakly by dynamical processes in the upper atmosphere and by electromagnetic disturbances related to magnetospheric variations. The E layer in the vicinity of its maximum is formed mainly by ionization of the atmosphere in two relatively narrow solar spectral intervals near 6 nm and 100 nm.

Measurements of the short-wavelength radiation in this region are sufficiently reliable [Torr and Torr, 1985]. However, there is significant uncertainty in some spectral ranges, and the ionospheric response to each of these ranges may be considered separately on the basis of more detailed theories of ionospheric formation developed recently.

The opportunity to conduct long-term (during several solar cycles) ground-based measurements (mantaining during that period the same measurement accuracy) is the principal advantage of using ionospheric measurements as compared to direct solar flux measurements on a satellite.

On the basis of the spectral model [Bruevich and Nusinov, 1984] and E region ionization theory, Nusinov [1988] developed an E layer model which describes with a good accuracy variations of the principal E layer parameters with solar activity and geophysical conditions. The Bruevich and Nusinov [1984] model was developed with allowance for the behavior of E layer critical frequencies, that is, the ionospheric data were used to obtain additional information about relatively small parts of the spectrum, which govern the ionization in the layer maximum. The intensity in the spectral ranges, which do not contribute significantly to ionization in the vicinity of the E or F region maxima, has not until now been able to be corrected by ionospheric data.

The aim of this paper is to specify the values of radiation fluxes in the 10- to 30-nm range on the basis of comparison of calculations with the Nusinov [1988] ionospheric model to studies of the interlayer ionization valley ( E and F1 ), where this radiation provides the main part of the ionization rate.

Observational Results and Valley Empirical Models

The value of the minimum electron concentration in the interlayer ionization valley, n_ev is one of the most important parameters of the upper part of the E layer. An analysis of a large number of the n_e(h) profiles was presented by Shlionskiy [1982], who obtained the following formula for the n_ev/n_em ratio ( n_em is the E -layer maximum electron concentration):

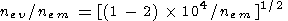(1)

for n_em > 3 10⁴ cm ^-3 (which corresponds to daytime conditions). The comparison with data from the Chasovitin et al. [1983] and Fatkullin et al. [1981] empirical model demonstrated that the above formula describes well the empirical model data for various seasons, local times, and solar activity levels. The calculations of n_e/n_v by the Fatkullin et al. [1981] empirical model also almost coincide with (1). Since, as a rule, in the daytime n_em > 3 10⁴ cm^-3, one can approximate relation (1) in the form:

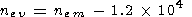(2)

One can see from (2) that the value of n_ev under very different conditions is lower that n_em by 1.2 10⁴ cm^-3.

Let us introduce a parameter that characterizes the relative depth of the valley: V = (n_em - n_ev)/n_em. Analysis of the Fatkullin et al. [1981], Rawer et al. [1978], and GOST [1990] empirical models has shown that the value of V for low solar zenith angles c< 60^o is nearly independent of solar zenith angle, season, and solar activity. For example (at middle latitudes) in the International Reference Ionosphere (IRI) model [Rawer et al., 1978] V = 0.05, in the Russian reference model [Chasovitin et al., 1983; GOST, 1990] V =0.15, and in the Fatkullin et al. [1981] model V = 0.13.

Thus the c< 60^o interval, which has a lower scatter of the V values according to various empirical models, is apparently less influenced by the geophysical factors and can be used to compare the empirical values of V and the values calculated by the theoretical model under various fluxes in the 20- to 30-nm spectral range ( I_20-30 ).

Model Calculations of Valley Parameters

Comparison of the results (1) and (2) of the empirical modeling with calculations by the Nusinov [1988] model demonstrates that if the Bruevich and Nusinov [1984] spectrum is used, the difference between n_ev and n_em is much more than the difference obtained from the empirical models. An example of such calculation for F_10.7 = 120 is shown in Figure 1 (dashed lines). The electron temperature T_e in the valley was taken to be equal to the atmospheric temperature T_n according to the incoherent scatter data (see, for example, Klyueva [1982]).

Analysis of various versions of calculations shows that the increase of the n_ev value under alteration of the input parameters occurs almost completely due to an increase of the radiation intensity I_10-30 in the narrow range 10-30 nm. Figure 1 shows as an example the results obtained under various solar zenith angles c with the doubled I_10-30 intensity. It can be seen that under the flux doubling n_e increases only above the E layer maximum and n_em does not change significantly. Analysis of the calculations has shown that the value of n_em - n_ev = 1.2 10⁴ cm ^-3 corresponds to an increase of I_10-30 on the average by 2.5 times (from 2.18 for c = 30^o to 2.56 for c = 75^o ; for c = 75^o the height of the minimum concentration in the valley exceeds 130 km and above that level the difference between T_e and T_n should be taken into account). Let us consider the question of the I_10-30 increase in more detail.

It follows from (2) that the relative depth of the valley V = 1.2 10⁴/n_em. Since under almost all geophysical conditions n_e < 2 10⁵ cm^-3, the value of V should exceed 0.06. As a rule the IRI model [Rawer et al., 1978], for which the valley depth V is always small and less than 0.05, does not satisfy this condition.

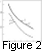The calculated values of V depend on the relation between the radiation intensity in various spectral ranges: 97.7-nm and 102.6-nm lines forming the E layer maximum and the 10- to 30-nm interval forming the valley. Figure 2 shows the results of V calculations as a function of the K coefficient value, which indicates by how much the intensity in the 10- to 30-nm interval was increased in comparison to the model spectrum by Bruevich and Nusinov [1984], K = 1 corresponding to the spectral flux values obtained on board the AE-E satellite.

The calculations were performed for 1200 LT in summer at middle latitudes ( f = 45^o ) under high ( F_10.7 = 190 ) and low (F_10.7 = 65 ) solar activity. The values of V according to the Fatkullin et al. [1981] and GOST [1990] empirical models are also shown in Figure 1. One can see that agreement between the theoretical model and the empirical models is reached under K = 1.9 under solar minimum and K = 3.1 under high solar activity. On average the necessary increase of the flux is K = 2.5. A use for a similar comparison of the Rawer et al. [1978] model requires under high activity even higher (and probably unreal) values of K (under solar activity minimum the value of K = 4.5 would be needed). It is worth noting that variations of the radiation fluxes in the 25- to 30-range do not influence the calculated valley parameters; so the conclusion on the necessary increase of the radiation flux by 2.5 times refers (as was the case in the work of it Richards and Torr [1984, 1985]) to the 10- to 25-nm spectral interval.

It should be noted that the residual n_em - n_ev = 1.2 10⁴ cm ^-3 may also be obtained by decreasing I_97.7, I_102.6, and I_0.1-10 (i.e., because of a decrease of n_em ). In that case the values n_em would be lower than the ones observed by vertical sounding and reliably reproduced by the Nusinov [1988] model.

Principally, to get empirical values of V, one can increase the intensity of the spectral interval 30 < l< 100 nm, which forms the F region. However, the numerical simulation of the ionospheric F region by Forster et al. [1995] shows that the fluxes in the above mentioned region, obtained from the Bruevich and Nusinov [1984] spectral model, provide a good agreement of the calculations and observations. Buonsanto [1990] compared the n_e profiles calculated from the photochemical model of the ionosphere at 100-200 km with the profiles measured by the incoherent scatter method at the Millstone Hill site. However, an uncertain conclusion about the radiation flux in the l< 25 nm range was arrived at: either an increase the UV flux in the entire wavelength range by 30% in comparison with the values accepted by Shlionskiy [1982], or an increase of the flux in the l< 25 nm range by 2 times were needed.

Let us consider in detail the question on variations of the radiation flux in the 10- to 30-nm range with solar activity. According to the SERF 2 [Tobiska and Eparvier, 1998] and Hinteregger et al. [1991] models using parameters as published by Woods and Rottman [1990] models, based mainly on the measurements of the AE-E satellite, this flux is about 2.3 and 2.6 times, respectively, lower than the flux according to the Bruevich and Nusinov [1984] model at low solar activity. Under high solar activity the fluxes in the Bruevich and Nusinov [1984] and SERF 2 models are close, and in the Hinteregger model the fluxes are lower by 1.5 times than the Bruevich and Nusinov [1984] model. Thus according to the SERF 2 and Hinteregger models the flux in the 10- to 30-nm range exhibits stronger changes with activity than according to the Bruevich and Nusinov [1984] model.

The analysis of the empirical ionospheric models presented above also indicates a stronger dependence of the radiation in the 10- to 30-nm range on solar activity than is given by the Bruevich and Nusinov [1984] model. Actually, one can see from Figure 2 that according to the ionospheric models K = 2 under low activity and on average K = 3 under high activity, that is, the flux in the 10- to 30-nm range increases by about 1.5 times more strongly than the fluxes at 97.7 nm and 102.6 nm. Since, however, there exist in this range both coronal emissions, which change very strongly with solar activity, and chromospheric emissions, a certain conclusion on the increase rate in particular spectral regions 10-30 nm can hardly be drawn.

Conclusion

It follows from this study of the upper part of the E region and the interlayer ionization valley that the intensity of the solar spectrum in the 10- to 30-nm range should be increased by about 2.5 times in comparison to the AE-E data. This result was obtained using the Bruevich and Nusinov [1984] model spectrum. To match ionospheric data, it is enough to increase the corresponding solar flux coefficients by 2.5 times. The above conclusion agrees with the results by Richards and Torr [1984, 1985], who on the basis of comparison of measured and calculated photoelectron spectra demonstrated a need for an increase of I_10-25 by about 2 times the AE-E values [Torr et al. 1979].

Acknowledgments

References

Bruevich, E. A., and A. A. Nusinov, The spectrum of the short-wave radiation for aeronomical calculations under various levels of solar activity, Geomagn. Aeron., 24 (4), 581, 1984.

Buonsanto, M. J., A study of the daytime E-F1 region ionosphere at midlatitude, J. Geophys. Res., 95 (A6), 7735, 1990.

Chasovitin, Yu. K., V. B. Shushkova, E. N. Sykilinda, and V. V. Maksimova, Empirical model of the electron concentration for low and middle latitudes at altitudes of 80-200 km, Proceedings of the Experim. Meteor., 13 (102), 59, 1983.

Fatkullin, M. N., et al., Empirical Models of the Midlatitude Ionosphere, 256 pp., Nauka, Moscow, 1981.

Forster, M., V. Mikhailov, A. Mikhailov, and J. Smilauer, A theoretical interpretation of ion composition measured on board the "Active" satellite in the European sector during April 10-12, 1990, geomagnetic storm, Ann. Geophys., 13 (6), 608, 1995.

GOST, Terrestrial Ionosphere: Model of Global Distribution of Concentration, Temperature, and Effective Collision Frequency of Electrons, 812 pp., Izd. Standartov, Moscow, 1990.

Hinteregger, H. E., K. Fukui, and B. R. Gilson, Observational, reference and model data on solar EUV from measurements on AE-E, Geophys. Res. Lett., 8, 1147, 1991.

Klyueva, N. M., Variations in the electron temperature at the 110-200 km altitudes according to the incoherent scatter data, Proceedings of the Experim. Meteor., 11 (95), 47, 1982.

Nusinov, A. A., Determinate model of the midlatitude and equatorial E layer (description and relative accuracy estimates), Ionosfernye Issled., 44, 94, 1988.

Rawer, K., S. Ramakrishan, and D. Bilitza, International Reference Ionosphere, IRI 1978, Union Radio Scientifique Internationale, Brussels, 1978.

Richards, P. G., and D. G. Torr, An investigation of the consistency of the ionospheric measurements of the photoelectron flux and solar EUV flux, J. Geophys. Res., 89 (A7), 5625, 1984.

Richards, P. G., and D. G. Torr, The altitude variation of the ionospheric photoelectron flux: A comparison of theory and measurement, J. Geophys. Res., 90 (A3), 2877, 1985.

Shlionskiy, A. G., On a possible forecast of the parameters of the interlayer ionization minimum on the basis of their dependence on f_oE, in Spatial-Temporal Structure of the Lower Ionosphere, p. 82, IZMIRAN, Moscow, 1982.

Siskind, D. E., et al., On the relationship between the solar soft X ray flux and thermospheric nitric oxide: An update with an improved photoelectron model, J. Geophys. Res., 100, 19,687, 1995.

Tobiska, W. K., and F. G. Eparvier, Improvements to EUV irradiance modeling in the soft X rays and FUV 97 Solar Physics, 177, 147, 1998.

Torr, M. R., and D. G. Torr, Ionization frequencies for solar cycle 21: Revised, J. Geophys. Res., 90 (A7), 6675, 1985.

Torr, M. R., D. G. Torr, R. A. Ong, and H. E. Hinteregger, Ionization frequencies for major thermospheric constituents as a function of solar cycle 21, Geophys. Res. Lett., 6 (10), 771, 1979.

Winningham, J. D., et al., Energetic (>60 eV) atmospheric photoelectrons, J. Geophys. Res., 94, 15,335, 1989.

Woods, T. N., and G. J. Rottman, Solar EUV irradiance derived from a sounding rocket experiment on November 10, 1988, J. Geophys. Res., 95 (A5), 6227, 1990.