 We used the series of the annual means of the
aa indices of
geomagnetic activity from 1863 to 1993 and Wolf's numbers ( W ) from
1850 to 1993 (Figure 1) from
Solar-Geophysical Data Prompt Reports (1993-1994).
We used the series of the annual means of the
aa indices of
geomagnetic activity from 1863 to 1993 and Wolf's numbers ( W ) from
1850 to 1993 (Figure 1) from
Solar-Geophysical Data Prompt Reports (1993-1994).
Yu. R. Rivin
Institute of Terrestrial Magnetism, Ionosphere, and Radio Wave Propagation, Troitsk, Moscow Region, Russia
The magnetic field of the Sun changes its polarity from one 11-year cycle to another forming the 22-year cycle. In publications on solar activity the 22-year cycle is usually termed a "magnetic" cycle. Attempts to reveal the magnetic cycle in variations of strength of the geomagnetic field F and geomagnetic activity (GA) are known [Chernovsky, 1966; Chirkov and Samsonov, 1984; Dumbold, 1972; Livshits, 1982; Rivin, 1989; Zaretskiy, 1982]. Most of the attempts are based on consideration of differences in properties of the considered objects in the even-numbered and odd-numbered cycles. These differences, as a rule, are insignificant, and the cycles are limited in number (5-6 pairs) to enable us to analyze the properties of the magnetic cycle of GA and the mechanism of its generation.
Below we show how the 22-year cycle of GA was separated out by two methods, and we consider its main properties and their differences from the properties of the magnetic cycle in Wolf's numbers characterizing the solar activity. The source of this cycle is also discussed.
 We used the series of the annual means of the
aa indices of
geomagnetic activity from 1863 to 1993 and Wolf's numbers ( W ) from
1850 to 1993 (Figure 1) from
Solar-Geophysical Data Prompt Reports (1993-1994).
We used the series of the annual means of the
aa indices of
geomagnetic activity from 1863 to 1993 and Wolf's numbers ( W ) from
1850 to 1993 (Figure 1) from
Solar-Geophysical Data Prompt Reports (1993-1994).
According to
Rivin [1986, 1989],
the
aa index series has the
following significant different features in comparison with the
W series:
(1) the correlation of the amplitude of the 11-year cycle and of
shorter-period variations is much smaller in it;
(2) at the end of the curve, the
amplitude of the cycle is so small that the cycle can be considered
practically absent; the variations of the index curve for this
period are presented only by the variation with
T 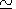 6 years;
(3) the
variations with
T
6 years;
(3) the
variations with
T 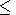 11 years are superimposed on the trend;
and
(4) the
magnetic cycle in geomagnetic activity is not seen.
11 years are superimposed on the trend;
and
(4) the
magnetic cycle in geomagnetic activity is not seen.
To be sure that the description of properties of the magnetic cycle of geomagnetic activity is valid, two of the most well-known long-term series of the annual means of the indices of GA, obtained by other methods, were additionally considered: (1) C9 , the index from the data of the Pavlovsk-Voeykovo observatory for the years 1841 to 1975 [Zosimovich, 1981], the lacunas being linearly interpolated; and (2) Ki , the index from the Potsdam-Niemegk observatory data for years 1890 to 1985 [Lenners and Zander, 1987].
By "traditional method" we mean the digital filtration of the initial series without reconstruction (see below) of the initial data. On smoothing of the aa index series by a running interval of 11 years, the low-frequency (lf) and high-frequency (hf) (the difference of the initial and smoothed curves) parts of variations of the aa index have been derived (Figure 1).
The curve ( aa) lf characterizing the
lf part shows the increase of the
aa index since the end of the past century to present (trend) with
superimposed variation with
T 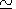 20 years. This variation is clearly
seen in the beginning ( W cycles 12 and 13) and at the end
(cycles 18-21)
of the curve where, accounting for the amplitude-frequency
characteristics of the smoothing,
aa
20 years. This variation is clearly
seen in the beginning ( W cycles 12 and 13) and at the end
(cycles 18-21)
of the curve where, accounting for the amplitude-frequency
characteristics of the smoothing,
aa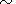 4.
In the first half of the
twentieth century the amplitude of this variation is less and veiled by the linear
part of the trend. The phase of this variation, which can be identified
with the magnetic cycle, is shifted with respect to the magnetic cycle in
W by
4.
In the first half of the
twentieth century the amplitude of this variation is less and veiled by the linear
part of the trend. The phase of this variation, which can be identified
with the magnetic cycle, is shifted with respect to the magnetic cycle in
W by
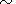 p /2 .
p /2 .
The high-frequency part of the filtration curve
aa hf is additionally
smoothed by an interval of 3 years. It contains basically the 11- and 6-
year variations with amplitude aa ~4-5. The variation with
T 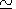 20 years is partially left in
the hf part, however, in places of
enhancement its contribution does not exceed
aa
20 years is partially left in
the hf part, however, in places of
enhancement its contribution does not exceed
aa 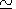 1 . Thus the
frequency composite signal was separated out as the hf part with the
11-year cycle prevailing in the interval. Unlike the cycle of Wolf's
numbers, it has no 22-year variation in amplitude modulation.
1 . Thus the
frequency composite signal was separated out as the hf part with the
11-year cycle prevailing in the interval. Unlike the cycle of Wolf's
numbers, it has no 22-year variation in amplitude modulation.
The above mentioned properties of the frequency composition of the aa index variations are largely similar to those of the solar activity variations which were interpreted by Rivin [1993, 1994]. It permits assuming that the frequency structure of the aa index series, like that of the W series, is the result of linear detection of the 22-year cycle of the solar magnetic field, specifically, of its poloidal component.
When using this method of separation, the properties of the magnetic cycle of GA can be described only qualitatively: there exists the amplitude modulation and the phase shift relative to the magnetic cycle of W . Therefore for a more accurate and complete description it would be necessary to construct the 22-year variation of GA based on the available experimental data. But before using one such method, it is necessary to be sure that the aa index is adequate for the description of the cyclic variations of geomagnetic activity.
The difference in behavior of the 11- and 22-year variations of GA in the indices ( aa and M(Kp) ) was shown by Rivin [1986, 1989]. The index M(Kp) was introduced by Ol' [1969] but has no wide acceptance. Considering past experience, the analysis of properties of the magnetic cycle of GA was carried out over several indices of geomagnetic activity, derived by different methods (Figure 1).
The hf parts of the three smoothed indices behaving accordingly
(in the interval from 1896 to 1973 the coefficient of the linear
correlation
r 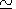 0.8 ), their phase and amplitude
modulation are
similar. A comparison of the smoothed lf parts for the different indices
gives the less concordant behavior, though for all indices the variation
with
T
0.8 ), their phase and amplitude
modulation are
similar. A comparison of the smoothed lf parts for the different indices
gives the less concordant behavior, though for all indices the variation
with
T 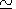 20 years is separated out here. The
trend is significant
and changes identically in the
aa and
Ki indices, but it is practically
absent in the
C9 index. The reason for that is possibly related to the
different techniques of obtaining the
K and
C9 indices: the
K index
is derived as the maximal deviation inside the 3-hour interval, from where
the quiet daily variation is then excluded, whereas
C9 is the maximal
deviation during the day.
20 years is separated out here. The
trend is significant
and changes identically in the
aa and
Ki indices, but it is practically
absent in the
C9 index. The reason for that is possibly related to the
different techniques of obtaining the
K and
C9 indices: the
K index
is derived as the maximal deviation inside the 3-hour interval, from where
the quiet daily variation is then excluded, whereas
C9 is the maximal
deviation during the day.
Thus the analysis of variations of three different indices of GA shows that the description of variations in the hf part of smoothing as well as of variations of the magnetic cycle in the trend is reliable. The trend itself is present only in the indices aa and Ki .
It was shown by
Rivin [1993, 1994]
when analyzing the series of
Wolf's numbers, that in the interval of the past 400 years this series
describes the amplitude and frequency variations of the magnetic cycle,
whereas the variations of solar activity with
T 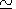 11 and
T
11 and
T 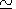 6 years
result from detecting the initial process (the variation of
the toroidal magnetic field), which is accomplished by the
observational method. It was assumed above that the 11- and 6-year
variations of geomagnetic activity as well as other variations of the
aa series are also the result of the detection
of the
22-year cycle of the poloidal component of the global magnetic field of
the Sun. Here the mechanism of the detection is different in comparison with
the case of solar activity.
6 years
result from detecting the initial process (the variation of
the toroidal magnetic field), which is accomplished by the
observational method. It was assumed above that the 11- and 6-year
variations of geomagnetic activity as well as other variations of the
aa series are also the result of the detection
of the
22-year cycle of the poloidal component of the global magnetic field of
the Sun. Here the mechanism of the detection is different in comparison with
the case of solar activity.
To obtain the magnetic cycle in the data of GA using the reconstruction of initial data, we can use the reconstruction of the magnetic cycle in W numbers on the basis of the Gnevyshev-Ol' rules [Gnevyshev and Ol', 1948; Rivin, 1993, 1994].
We assume that the 22-year cycle, as well as the magnetic cycle of W , consists of pairs of 11-year cycles beginning with the even-numbered cycle. We calculate the sum of the annual means of aa , C9 and Ki indices as was done by Gnevyshev and Ol' [1948]. According to Rivin [1989], we assume in the process that, first, the boundaries of the cycle are determined by the epochs of minimums of Wolf's numbers, whereas the epochs of minimums for the cycles of GA and W are coincident (we neglect the shift by 1 year since it has little effect on the relative change of the sum) and, second, owing to the more complex structure of the amplitude spectrum of the annual means of the GA indices, the sums or cycle-averaged values are more preferable for the analysis than the maximal values, as was done for W .
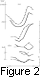 Figure 2a shows separately the sums of the even-numbered and
odd-numbered cycles of the Wolf's numbers (the Zurich observatory
numbering) and of three indices of geomagnetic activity. The behavior
of the cycles
SW reflects one of the
Gnevyshev and Ol' [1948]
rules
the
SW of the odd-numbered cycles systematically
exceeds
the
SW of the even-numbered cycles. Similar
behavior is
exhibited by the cycles
Saa except for the pair 20 and 21 for
which the amplitude does not decrease in comparison to the previous
magnetic cycle, as occurs in the magnetic cycle of
W . In addition, the
relation of amplitudes of the even-numbered and odd-numbered cycle
also changes.
Figure 2a shows separately the sums of the even-numbered and
odd-numbered cycles of the Wolf's numbers (the Zurich observatory
numbering) and of three indices of geomagnetic activity. The behavior
of the cycles
SW reflects one of the
Gnevyshev and Ol' [1948]
rules
the
SW of the odd-numbered cycles systematically
exceeds
the
SW of the even-numbered cycles. Similar
behavior is
exhibited by the cycles
Saa except for the pair 20 and 21 for
which the amplitude does not decrease in comparison to the previous
magnetic cycle, as occurs in the magnetic cycle of
W . In addition, the
relation of amplitudes of the even-numbered and odd-numbered cycle
also changes.
On elimination of the trend (Figure 2b), the systematic distinction of the amplitudes of the even-numbered and odd-numbered cycles disappears, which significantly differs from the case of variations of the amplitudes of the even-numbered and odd-numbered cycles in the Wolf's numbers. The other important specific feature of the curves Saa and SKi in Figure 2b is a practically total absence of amplitude modulation (only a slight monotonous decrease to our days). The absence of modulation is more pronounced if one consider in each cycle the variations of the mean over even-numbered and odd-numbered cycles. At the same time the traces of modulation are present in the curve SC9 .
Thus there are principal differences of the 22-year cycle in the reconstructed curves of geomagnetic activity in comparison with the properties of the magnetic cycle of solar activity.
The most complete phenomenological model of the main constituents
of the 11-year cycle of geomagnetic activity was developed by
Legrand and Simon [1989].
They divided the GA into basic components with
independent solar sources, assuming that the main contribution to
the periodicity is due to the polar high-speed particle fluxes producing
the recurrent magnetic storms on Earth. The polar fluxes are the
most active during the
decreasing
phase
and minimum of the
solar cycle; therefore it was concluded that the cycle of geomagnetic
activity leads the cycle of solar activity by
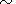 p in phase.
p in phase.
The phase shift
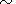 p /2 between
the magnetic cycles of GA
and
W , which was obtained above by another, more formal
method (namely, by filtration of the
aa ,
C9 , and
Ki index
series), corresponds not only morphologically to their ideas,
but deepens them owing to the understanding that the basis of
solar activity is the 22-year cycle. At the same time some
doubts arise concerning the unambiguousness of the interpretation of
Legrand and Simon [1989]
of the source of the 11-year (and,
hence, of the 22-year) periodicity of GA. Actually, according
to Figure 7 from
Legrand and Simon [1989],
in one interval the
mean number of days corresponding to high-speed fluxes (~7%),
is approximately an order of magnitude less than
the number of quiet days.
Under digital filtration, which is the procedure for obtaining the
annual means, such rare events must be largely filtered off and
have no pronounced effect on the cycle. At the same time, as
is shown in Figures 6 and 10 of
Legrand and Simon [1989],
the number of quiet days of GA increases in the vicinity
of the minimum of the 11-year cycle of solar activity. This fact
and the results presented by
Rivin [1996]
permit the
assumption that the main source of the magnetic cycle of
geomagnetic activity is not the polar fluxes causing the generation of
recurrent storms, but the corresponding variations of the main
parameters of the current sheet (thickness and convolution) which are
controlled by the 22-year cycle of the poloidal magnetic field of the Sun
at high latitudes. These variations modulate the velocity of the quiet
solar wind in the current sheet that is then transferred by the wind to
the magnetosphere of the Earth.
p /2 between
the magnetic cycles of GA
and
W , which was obtained above by another, more formal
method (namely, by filtration of the
aa ,
C9 , and
Ki index
series), corresponds not only morphologically to their ideas,
but deepens them owing to the understanding that the basis of
solar activity is the 22-year cycle. At the same time some
doubts arise concerning the unambiguousness of the interpretation of
Legrand and Simon [1989]
of the source of the 11-year (and,
hence, of the 22-year) periodicity of GA. Actually, according
to Figure 7 from
Legrand and Simon [1989],
in one interval the
mean number of days corresponding to high-speed fluxes (~7%),
is approximately an order of magnitude less than
the number of quiet days.
Under digital filtration, which is the procedure for obtaining the
annual means, such rare events must be largely filtered off and
have no pronounced effect on the cycle. At the same time, as
is shown in Figures 6 and 10 of
Legrand and Simon [1989],
the number of quiet days of GA increases in the vicinity
of the minimum of the 11-year cycle of solar activity. This fact
and the results presented by
Rivin [1996]
permit the
assumption that the main source of the magnetic cycle of
geomagnetic activity is not the polar fluxes causing the generation of
recurrent storms, but the corresponding variations of the main
parameters of the current sheet (thickness and convolution) which are
controlled by the 22-year cycle of the poloidal magnetic field of the Sun
at high latitudes. These variations modulate the velocity of the quiet
solar wind in the current sheet that is then transferred by the wind to
the magnetosphere of the Earth.
In the process of filtration carried out in this work, we
did not succeed
in separating out the trend from the magnetic cycle, which makes the
description difficult. However, analyzing the smoothed low-frequency
part of the GA indices in Figure 1, one can derive the amplitude
modulation of the 22-year cycle of geomagnetic activity by a
longer-term variation which is responsible for decreasing geomagnetic
activity in the end of the past century and first half of our century. As
in the case of solar activity
[Rivin, 1993, 1994]
where one of the
variations modulating the magnetic cycle is the secular fluctuation, we
can assume that the magnetic cycle of geomagnetic activity is
modulated by fluctuations with
T 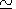 70 years
[Rivin, 1986, 1989].
70 years
[Rivin, 1986, 1989].
The significant distinction in the trend behavior between the aa and W curves shows itself in the different models of the magnetic cycles of both types of activities. As a first approximation, the model of the magnetic cycle W can be written in a form [Rivin, 1994, 1995]
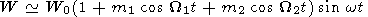 | (1) |
where
W1 = 2 p
/T1 ,
W2 = 2 p
/T2 ,
T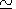 2300 years,
T
2300 years,
T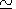 100 years,
m is
the corresponding coefficients of amplitude modulation,
w = 2 p /T
,
T
100 years,
m is
the corresponding coefficients of amplitude modulation,
w = 2 p /T
,
T 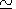 22 years,
W
22 years,
W
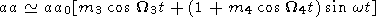 | (2) |
where
W4 = 2 p
/T4 and, according to
Rivin [1986, 1989],
T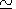 70 years,
W3 = 2 p
/T3 ,
it is possible that
T
70 years,
W3 = 2 p
/T3 ,
it is possible that
T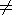 T
T
When reconstructing the 22-year cycle over the total aa index series (Figure 2a), the trend was included in the sums of indices over the cycle, thus resulting in conserving the external similarity of variations of the magnetic cycles of geomagnetic and solar activities over the whole interval except the last magnetic cycle. However, the analysis of the curves in Figure 2b shows that external similarity of the curves in Figure 2a is not due to the amplitude modulation of the 11-year cycle by the 22-year cycle, as it is for the curve SW , but due to the trend.
The amplitude modulation by variation with
T4 is absent in the
amplitudes
Saa and
SKi presented in Figure 2b; there
is
only a slight decrease to the end of the trend. In the same figure the
traces of such modulation are present in the curve
SC9 . If we
accept that the
K index (and hence the
aa index) describes the
geomagnetic activity more accurately compared to the
C9 index, we are
thus led to assume that the amplitude modulation of the 11-year
variation is shifted in phase by
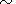 p relative
to the 6-year
modulation, and the additional enhancement of the latter takes place.
The possibility of this assumption is built up on the analysis of each
such variation separated out by methods of narrow-band filtration
[Rivin, 1989],
taking account of the following: (1) in cycles 20 and 21
the amplitude of the 11-year cycle of GA approaches zero, and
hence the sums of indices should
also
be
close to zero; (2) in the years
of absence of the 11-year cycle of GA the amplitude of the 6-year
variation is approximately equal to the amplitude of the 11-year cycle
and it is less when the 11-year cycle is present. Such situation does not
correspond to the linear detection of the 22-year cycle.
p relative
to the 6-year
modulation, and the additional enhancement of the latter takes place.
The possibility of this assumption is built up on the analysis of each
such variation separated out by methods of narrow-band filtration
[Rivin, 1989],
taking account of the following: (1) in cycles 20 and 21
the amplitude of the 11-year cycle of GA approaches zero, and
hence the sums of indices should
also
be
close to zero; (2) in the years
of absence of the 11-year cycle of GA the amplitude of the 6-year
variation is approximately equal to the amplitude of the 11-year cycle
and it is less when the 11-year cycle is present. Such situation does not
correspond to the linear detection of the 22-year cycle.
1. The 22-year variation of geomagnetic activity is modulated in
amplitude and shifted in phase by
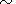 p /2 relative
to the
magnetic cycle in Wolf's numbers. Such properties, taking into
account the amplitude gradient, as well as the frequencies of
the recurrence of substorms agree with the assumption that the
magnetic cycle of geomagnetic activity is conditioned by the
variations of the high-latitude magnetic field, leading to the
modulation of the low-speed solar wind in the current sheath.
p /2 relative
to the
magnetic cycle in Wolf's numbers. Such properties, taking into
account the amplitude gradient, as well as the frequencies of
the recurrence of substorms agree with the assumption that the
magnetic cycle of geomagnetic activity is conditioned by the
variations of the high-latitude magnetic field, leading to the
modulation of the low-speed solar wind in the current sheath.
2. There are a number of specific features in the curves of the reconstructed magnetic cycle of geomagnetic activity which show the difference of the 22-year cycles of the toroidal and high-latitude poloidal components of the magnetic field of the Sun.
Chernovsky, E. Y., Double sunspot cycle variation in terrestrial magnetic activity, 1884-1963, J. Geophys. Res., 71 (3), 965, 1966.
Chirkov, N. P., and I. S. Samsonov, The 22-year periodicity of the solar wind and of geomagnetic activity, Geomagn. Aeron., 24 (2), 300, 1984.
Dumbold, T., The 22-year cycle in the recurrent tendency of geomagnetic activity, J. Interdisciplinary Cycle Res., 3 (3-4), 365, 1972.
Gnevyshev, M. N., and A. I. Ol', On the 22-year cycle of solar activity, Astron. Zh., 25 (1), 18, 1948.
Legrand, J.-P., and P. A. Simon, Solar cycle and geomagnetic activity: A review for geophysicists, part 1, The contributions to geomagnetic activity of shock waves and of the solar wind, Ann. Geophys., 7 (6), 565, 1989.
Lenners, D., and W. Zander, Summarized interpretation and valuation of the geomagnetic activity for the complete observational data series Potsdam-Seddin-Niemegk from 1890 to 1985, HHI Rep., 21, pp. 185-190, 1987.
Livshits, M. A., Geomagnetic activity during the even-numbered and odd-numbered 11-year cycles, Geomagn. Aeron., 22 (2), 335, 1982.
Ol', A. I., Indices of disturbance of the Earth's magnetic field and their solar-physical importance, Proc. Arctic Antarct. Res. Inst., 289, 5, 1969.
Rivin, Yu. P., Comparison of variations of the indices of solar and
geomagnetic activities at different frequencies in a range
10 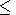 T
T 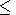 100 years,
Geomagn. Aeron., 26 (2), 353, 1986.
100 years,
Geomagn. Aeron., 26 (2), 353, 1986.
Rivin, Yu. P., The Cycles of the Earth and Sun, 165 pp., Nauka, Moscow, 1989.
Rivin, Yu. P., The main characteristics of the amplitude variation in the magnetic cycle of the Sun in Wolf's numbers and Shova's series over the past 500 years, Astron. Zh., 70 (6), 1257, 1993.
Rivin, Yu. P., The magnetic cycle of the Sun, in Problems of Solar Activity, edited by V. A. Dergachev, pp. 52-70, Phys.-Tech. Inst., St. Petersburg, 1994.
Rivin, Yu. P., The problem of description of the dynamics of the solar-spot magnetic fields in the cycle of activity, Izv. Akad. Nauk, Ser. Fiz., 59 (7), 43, 1995.
Rivin, Yu. P., In addition to the problem of division of the Earth's magnetic field into the parts corresponding to the external and internal sources, Geomagn. Aeron., 36 (3), 187, 1996.
Zaretskiy, N. S., The solar-magnetic cycle in geomagnetic activity, Geomagn. Aeron., 22 (3), 450, 1982.
Zosimovich, I. D., Geomagnetic Activity and Stability of the Corpuscular Field of the Sun, 191 pp., Nauka, Moscow, 1981.