International Journal of Geomagnetism and Aeronomy
Vol 1, No. 2, November 1998
Synthesis of the topside ionograms under the presence of isolated
irregularities in the bottomside ionosphere
N. P. Danilkin, V. I. Stasevich, and E. R. Tumanova
Institute of Applied Geophysics, Moscow, Russia
Contents
Abstract
A possibility is considered for determining parameters of
the ionospheric irregularities located below the
F region maximum
from the trace of the reflection from the ground, which is
observed in the ionograms of the topside sounding. The model of
the irregularities is described, and the results of the numerical
synthesis of topside ionograms in the presence of irregularities
with the given parameters are presented. A dependence of the
synthesized ionograms on the irregularity parameters (mutual
position of the satellite and irregularity, height above sea
level, intensity, and radius) is studied, and the types of ray
trajectories are shown.
Introduction
As a result of conducting active experiments, disturbances of
the electron concentration with characteristic dimensions of
kilometers and tens of kilometers and the development time of an hour
and longer are created. It is widely known that isolated
irregularities of a natural origin with nearly the same parameters
were observed
[Argo et al., 1992;
Calvert and Schmid, 1964;
Chidsey, 1965;
Fitzgerald et al., 1997].
The
ground-based ionospheric sounding is a reliable method of
detection of such irregularities
[Paul et al., 1968].
However,
this method cannot monitor the ionosphere above the
F region
maximum. It was noted earlier by
Danilkin et al. [1987a] that the
transionospheric sounding can be used to monitor
irregularities in the bottomside ionosphere using the traces in
the ionograms of satellite sounding.
The aim of this paper is to demonstrate that the topside sounding
itself provides abilities to observe the bottomside ionosphere
irregularities because of a presence in the ionograms of the trace
of the reflection from the ground.
There are methods of restoration of the vertical profile of the
undisturbed electron concentration on the basis of ionograms of
vertical, topside, and transionospheric sounding, but currently
there is no analogous solution of the inverse problem in the
presence in the ionograms of complicated traces formed by the
rays, refracted by irregularities. It is reasonable to use the
results of numerical solution of the direct problem of the
ionogram synthesis and to vary model parameters in order to get
maximum agreement with the experimental data.
Formulation of the Problem
The mathematical model of irregularities includes, in the same way
as was done by
Paul et al. [1968] and
Danilkin et al. [1987b],
a choice of a continuous function
F( r) , which tends to unity at
infinity and is superposed on the undisturbed spherically
layered distribution of the electron concentration:
F(h,d) = 1-A{1 + [(h-h0)2
+(d-d0)2 ]3/ R6}-1
where
h is the height above sea level;
d is the distance at
the ground,
h0 and
d0 are the height and distance of the
irregularity center, respectively;
R is a characteristic dimension
of the irregularity, and
A is the irregularity magnitude (describes
relative depletion of the electron concentration in the ( h0 ,
d0 )
point as compared to the undisturbed ionosphere).
The electron concentration vertical profile with a maximum at an
altitude of 300 km and critical frequency of 9.2 MHz typical for
middle latitudes was used as a background profile. The height of the
satellite orbit used in the calculations was 1000 km.
Methods of Calculations and Numerical Simulation Results
Radio wave propagation in the ionosphere was considered in the
geometric optics approximation (GOA). Application of the GOA and
the methods of ionogram synthesis in the presence of ionospheric
irregularities and of calculation of radio wave trajectories on
the basis of integration of a bicharacteristic system of
differential equations were described by
Danilkin et al. [1987a].
 Magnetic field influence leads to a splitting of the radio wave
into two components. In that case the system of the
bicharacteristic differential equations should be integrated
separately for each component; therefore two ionograms would be
synthesized, for the ordinary and extraordinary rays. For
diagnosis of the ionospheric irregularities it is also reasonable
to obtain experimental ionograms for both components, using the
polarization separation of the signals
[Danilkin, 1987]. To
simplify the calculations and make the results more visual, the
magnetic field influence was not taken into account in this work.
We will call the
trace of the reflection of the ordinary wave in the absence of
irregularities
the main ray. The rays refracted by
the irregularities form extra traces with a delay different from
that of the main ray. Depending on the irregularity dimension and
its position in the ionosphere and in relation to the satellites,
Magnetic field influence leads to a splitting of the radio wave
into two components. In that case the system of the
bicharacteristic differential equations should be integrated
separately for each component; therefore two ionograms would be
synthesized, for the ordinary and extraordinary rays. For
diagnosis of the ionospheric irregularities it is also reasonable
to obtain experimental ionograms for both components, using the
polarization separation of the signals
[Danilkin, 1987]. To
simplify the calculations and make the results more visual, the
magnetic field influence was not taken into account in this work.
We will call the
trace of the reflection of the ordinary wave in the absence of
irregularities
the main ray. The rays refracted by
the irregularities form extra traces with a delay different from
that of the main ray. Depending on the irregularity dimension and
its position in the ionosphere and in relation to the satellites,
 several types of ionograms are observed. Figures 1 and 2 show the
most characteristic ionograms. The influence of each of the irregularity
parameters chosen is considered, the rest of the parameters being
fixed.
several types of ionograms are observed. Figures 1 and 2 show the
most characteristic ionograms. The influence of each of the irregularity
parameters chosen is considered, the rest of the parameters being
fixed.
1. Let us denote as
Dd the modulus of the difference between
the distances of the satellite and irregularity at the Earth's
surface and consider its influence on the topside ionograms, using
as an example the irregularity with radius
R = 25 km,
altitude of the center
h0 = 200 km, and depth
A = 1 (which
corresponds to a "negative" irregularity with zero electron
concentration in the center). Under
Dd = 0 km (that is, when
the irregularity is situated at the vertical, which passes through
the Earth's center and the satellite), all the rays coming to the
reception point were refracted by the irregularity. There is no
main trace in this case, and the ionogram consists of two curves,
forming a "beak" with the sharp part directed to higher
frequencies (Figure 1b). The upper curve in Figure 1b is
formed by the rays propagating in the direction perpendicular to
the Earth. Passing the ionosphere, they cross the region with
depleted electron concentration; so their delay is less than the
delay of the main ray also propagating perpendicularly to the
Earth. Since the lower the radio wave frequency, the stronger
they are influenced by the irregularity, the difference in virtual
heights of the main (Figure 1a) and the upper (Figure 1b) traces
is maximum at a frequency of 9.2 MHz and is equal to 160 km. Under a
ray frequency increase the difference gradually decreases and is
almost within instrumental errors above 13 MHz. The lower
curve is due to the rays emitted from the satellite at a small
angle and returned
because of refraction by the irregularity.
Let us increase
Dd , that is, change the irregularity position
horizontally in relation to the satellite. The "beak" then becomes
narrower, and under
Dd 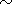 100 km
both curves almost
merge (the difference in the virtual height is comparable to the
instrumental errors) and the ionogram looks undisturbed.
100 km
both curves almost
merge (the difference in the virtual height is comparable to the
instrumental errors) and the ionogram looks undisturbed.
Further increase of
Dd leads to an increase of the
difference in altitudes of the main and extra traces by the
same value at any sounding frequency, and so the traces in the
ionogram in the frequency intervals, where the extra trace exists,
are similar (Figure 1a).
The trace's beginning and ending
frequencies (Figure 1a) also are
characteristic of an extra trace. The synthesis results have
demonstrated that with an increase of
Dd from 100 km and
higher, the length of the extra trace shortens: its beginning
frequency increases and its ending frequency decreases. For
example, for
Dd = 200 km, these values are 9.4 MHz
and 14.5 MHz.
2. To study the influence of the irregularity height above the ground,
ionograms for several values of this parameter were calculated.
The irregularity below 180 km does not influence radio wave
propagation, and no extra traces are seen in the ionograms. Under
the irregularity center height at 200 km, two extra short traces
parallel to the main trace appear at frequencies from 10.2 to
10.7 MHz and from 11.5 to 12 MHz. It may be assumed that there are
extra traces corresponding to the frequencies between the end of
the first trace and the beginning of the second one, and their
absence in the ionogram is due to incompleteness of the algorithm
used for a search of rays returned to the reception point. On the
basis of the ray trajectories, one can conclude that the
"low-frequency" and "high-frequency" extra traces are formed by
different types of rays. In the former case the descent and ascent
(after reflection from the ground) branches of the ray lay at
opposite sides from the irregularity center; in the latter case
they lay at the same side.
When the height of the irregularity center is from 250 km
to
300 km (the height of the electron concentration maximum), two extra
traces are well pronounced in the 10.5- to 15-MHz interval, one of
the traces being similar to the main trace and the other being
located so that it adjoins the main trace by its high-frequency
end and the first extra trace by its low-frequency end. The
topside ionogram and the ray trajectories, which lead to the
traces of such type, are presented in Figure 2a.
3. Let us discuss now the influence of
irregularity parameters
such
as radius and depth on the synthesized ionograms.
It can be seen from the above considered ionograms for disturbed
electron concentration that the extra traces in them are formed
mainly by two types of rays: first, the rays that crossed the
region situated within a characteristic volume of the
irregularity, and, second the rays that which were refracted
at the
irregularity outer boundary. These two types of rays should be
manifested in the ionogram by two extra traces. However, if the
residual of the virtual heights of these two traces is small
(within instrumental error), actually only one extra trace
would be seen in the ionogram. For example, at altitudes of
h0 = 200 km (Figure 1a), both rays refracted by the irregularity
and
returned to the reception point have traces with almost the same
virtual heights. We will call the trace of the rays that crossed
the irregularity the first extra trace, and we will call
the trace of the
rays refracted by the irregularity boundary the second extra
trace. The ionograms in Figures 1a, 1b and 2a were synthesized for
an irregularity with a characteristic dimension of
R = 25 km. The
ray trajectories are significantly different for the
irregularities with smaller or larger dimensions. Under the
irregularity dimension from 10 km to 50 km the position of the
second extra trace is slightly changed owing to a small change of
the ray path. However, the first extra trace is subjected to the
stronger influence of the irregularity dimensions: its virtual
height would be lower if the rays pass through the negative
irregularity of larger dimensions with depleted concentration (the
trace is situated higher in the ionogram) and
would be higher if the
irregularity dimensions are smaller. It is found that the
difference between the virtual heights of the first and second
extra traces at the 10.5-MHz frequency is about 10 km for the
irregularity with
R = 15 km. If
R = 25 km and 30 km and the other
parameters are the same, the height difference increases to 20 km
and 30 km, respectively. The traces merge at a frequency of
about 12 MHz. The irregularities with the characteristic dimension
of 50 km influence the rays passing through them so strongly that
the reduced height of the extra trace becomes lower than that of
the main trace (Figure 2b).
Considered above were ionograms synthesized for
irregularities with depth
A = 1 , that is, with zero
electron concentration in its center. The synthesis results show
that the higher the
A parameter, the more high-frequency rays
are influenced by the irregularity. For example, the extra trace
of the irregularity in Figure 1a under
A = 1 stops at a frequency
of 14 MHz, under
A = 0.7 it stops at 12 MHz, and under
A = 0.3 it
stops at 9.8 MHz.
Conclusions
Principal possibilities for diagnosing irregularities of the
bottomside ionosphere mainly of artificial origin on the basis of
characteristic features of the topside sounding signals reflected
from the ground are demonstrated. Solution of the corresponding
direct problem and comparison of the experimental data with
synthesized ionograms may provide determination of irregularity
location, dimensions, and depth.
References
Argo, P., T. J. Fitzgerald, and R. Carlos,
NICARE I HF propagation experiment results and interpretation,
Radio Sciences, 27, 289-305, 1992.
Calvert, W., and C. Schmid, Spread
F observations by the Alouette
topside sounder satellite,
J. Geophys. Res., 69 (9), 1839, 1964.
Chidsey, I., Evidence of ionospheric inhomogeneities over Wallops
Island,
Memo. Rep. 1700,
Ballistic Res. Lab.,
1965.
Danilkin, N. P., System radiosounding as a basis of the
ionospheric monitoring service, in
Ionospheric-Magnetic Service, p. 57, Gidrometeoizdat,
Leningrad, 1987.
Danilkin, N. P., et al., Diagnostics of local ionospheric
irregularities by the transionospheric sounding method,
in
XV National Conference on Radio Wave Propagation, Abstracts, p. 23,
Nauka, Moscow, 1987a.
Danilkin, N. P., D. S. Lukin, and V. I. Stasevich, Trajectory
synthesis of ionograms under presence of the artificial
ionospheric irregularities,
Geomagn. Aeron., 27 (2), 217, 1987b.
Fitzgerald, T. J., P. E. Argo, and R. C. Carlos,
Effects of artificially modified ionospheres on HF propagation:
Negative Ion Cation Release Experiment 2 and CRRES
Coqui experiments, Radio Sci., 32, 579-591, 1997.
Paul, A. K., G. G. Smith, and J. B. Wright, Ray tracing synthesis
of ionogram observations of a large local disturbance in the
ionosphere, Radio Sci., 3 (1), 15, 1968.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.2.0) on November 4, 1998.
 Magnetic field influence leads to a splitting of the radio wave
into two components. In that case the system of the
bicharacteristic differential equations should be integrated
separately for each component; therefore two ionograms would be
synthesized, for the ordinary and extraordinary rays. For
diagnosis of the ionospheric irregularities it is also reasonable
to obtain experimental ionograms for both components, using the
polarization separation of the signals
[Danilkin, 1987]. To
simplify the calculations and make the results more visual, the
magnetic field influence was not taken into account in this work.
We will call the
trace of the reflection of the ordinary wave in the absence of
irregularities
the main ray. The rays refracted by
the irregularities form extra traces with a delay different from
that of the main ray. Depending on the irregularity dimension and
its position in the ionosphere and in relation to the satellites,
Magnetic field influence leads to a splitting of the radio wave
into two components. In that case the system of the
bicharacteristic differential equations should be integrated
separately for each component; therefore two ionograms would be
synthesized, for the ordinary and extraordinary rays. For
diagnosis of the ionospheric irregularities it is also reasonable
to obtain experimental ionograms for both components, using the
polarization separation of the signals
[Danilkin, 1987]. To
simplify the calculations and make the results more visual, the
magnetic field influence was not taken into account in this work.
We will call the
trace of the reflection of the ordinary wave in the absence of
irregularities
the main ray. The rays refracted by
the irregularities form extra traces with a delay different from
that of the main ray. Depending on the irregularity dimension and
its position in the ionosphere and in relation to the satellites,
 several types of ionograms are observed. Figures 1 and 2 show the
most characteristic ionograms. The influence of each of the irregularity
parameters chosen is considered, the rest of the parameters being
fixed.
several types of ionograms are observed. Figures 1 and 2 show the
most characteristic ionograms. The influence of each of the irregularity
parameters chosen is considered, the rest of the parameters being
fixed.
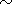 100 km
both curves almost
merge (the difference in the virtual height is comparable to the
instrumental errors) and the ionogram looks undisturbed.
100 km
both curves almost
merge (the difference in the virtual height is comparable to the
instrumental errors) and the ionogram looks undisturbed.