International Journal of Geomagnetism and Aeronomy
Published by the American Geophysical Union
Vol. 1, No. 1, April 1998
Determination of the electron density profile of the ionospheric
Alfvén resonator from the spectral structure of series of
Pc 1 geomagnetic pulsations
K. Prikner
Geophysical Institute, Acad. Sci. Czech Republic, Prague
F. Z. Feygin and D. S. Fligel
Institute of Physics of the Earth, Moscow
Abstract
Introduction
Experimental Data and Processing Method
Discussion
Conclusions
Acknowledgments
References
Abstract
A method for numerical simulation of the frequency
dependence of the reflection coefficient of ion-cyclotron waves
from the ionospheric layer based on observations of the Pc 1
geomagnetic pulsations (
f 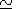 0.2-5
Hz) at the Kerguelen,
Sogra, and Nurmijarvi observatories is examined. Vertical profiles
of the electron density
Ne(Z) are determined from ground-based
observations of simultaneous Pc 1 series. The obtained profiles
Ne(Z) are compared with the models of ionospheric
Ne(Z) under low solar activity.
0.2-5
Hz) at the Kerguelen,
Sogra, and Nurmijarvi observatories is examined. Vertical profiles
of the electron density
Ne(Z) are determined from ground-based
observations of simultaneous Pc 1 series. The obtained profiles
Ne(Z) are compared with the models of ionospheric
Ne(Z) under low solar activity.
Introduction
In recent years, the idea of an Alfvén maser developed by
Belyaev et al.
[1984, 1985, 1987, 1990a] and
Belyakov et al. [1983] has
gained wide recognition, contributing considerably to the theory of
the generation of type Pc 1 (
f 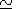 0.2-5
Hz) geomagnetic
pulsations ("pearls"). The mechanism is based on solving the
self-consistent problem of the interaction of Alfvén waves with hot
anisotropic protons on field lines with footpoints in conjugate
ionospheres. Using the "realistic" properties of the medium, the
aforesaid authors were able to explain the formation of the
structured emission, a long-standing mystery in the theory of
generation of the "pearls". These authors considered the
quasi-linear interaction of Alfvén waves with hot anisotropic
protons and precipitation of the latter into the ionosphere
(ensuring the auxiliary ionization), which led them to interpret
the fine effects of the dynamical spectrum of the "pearls"
differently from the mechanism earlier proposed by
Feygin and Yakimenko [1970] and
Gendrin et al. [1971].
0.2-5
Hz) geomagnetic
pulsations ("pearls"). The mechanism is based on solving the
self-consistent problem of the interaction of Alfvén waves with hot
anisotropic protons on field lines with footpoints in conjugate
ionospheres. Using the "realistic" properties of the medium, the
aforesaid authors were able to explain the formation of the
structured emission, a long-standing mystery in the theory of
generation of the "pearls". These authors considered the
quasi-linear interaction of Alfvén waves with hot anisotropic
protons and precipitation of the latter into the ionosphere
(ensuring the auxiliary ionization), which led them to interpret
the fine effects of the dynamical spectrum of the "pearls"
differently from the mechanism earlier proposed by
Feygin and Yakimenko [1970] and
Gendrin et al. [1971].
One of the components of the Alfvén maser is the ionospheric
resonant cavity
[ Lysak, 1988] or the ionospheric Alfvén resonator
[ Polyakov and Rapoport, 1981;
Prikner and Vagner, 1990], numerical
simulation of which is reported by Ostapenko and Polyakov [1990],
Prikner and Vagner [1983], and
Rudenko [1990]. Resonance properties
of the ionospheric cavity result in the fact that the reflection
coefficient R
is a function of frequency and has clearly pronounced
peaks. Wave generation takes place in a narrow frequency band near
one of the maxima of the reflection coefficient in multiple passage
of a signal through the region of amplification. These ideas led
Feygin et al. [1994] and
Nekrasov et al. [1991] to attempt a search
for simultaneous series of "pearls" propagating along the flux
tube. These authors suggested that the central frequencies of the
"pearls" observed simultaneously on the given station correspond to
maxima of the reflection coefficient, and the difference between
the central frequencies of the series of one event (consisting of
several series) is similar to the frequency difference between the
reflection coefficient peaks. In addition,
Feygin et al. [1994] and
Nekrasov et al. [1991] also considered other possible mechanisms
for the generation of simultaneous (parallel) Pc 1 series with
similar frequencies, e.g., the possibility of Pc 1 generation in
different regions of the magnetosphere and their propagation over
different L shells, and also the effect of the heavy ions He+
and O+ on the propagation of the ion-cyclotron waves (Pc 1 pulsations)
near gyrofrequencies of these ions. In both cases, the picture of
the wave process would differ significantly from that actually
observed.
The idea of reconstructing the ionospheric electron density profile
over the maximum of the
F2
layer was first put forward and
substantiated by observations of spectral resonance structures of
atmospheric electromagnetic noise in the frequency range 0.5-10 Hz
by Belyaev et al. [1990b].
In this paper, we employ the method of ionospheric modeling
[ Prikner and Fligel, 1991, 1992, 1993]
for determination of the
electron density profile
Ne(Z)
of the ionospheric Alfvén resonator
from the spectral structure of the series of Pc 1 geomagnetic
pulsations on the assumption that the characteristics of reflection
at conjugate points are similar during the occurrence of these
pulsations.
Experimental Data and Processing Method
In our work we used dynamical spectra of ten Pc 1 events observed
at the Kerguelen (49o 21'S, 70o 12'E,
geographic;
L = 3.7 )
and Sogra ( 62o 48'N,
46o 15'E, geographic; L = 3.6 )
observatories in 1964-1966, and at the Nurmijarvi
( 60o 30'N,
24o 42'E, geographic;
L = 3.5 ) observatory in 1977
[ Nekrasov et al., 1991].
All the events observed featured two to four
simultaneous Pc 1 series having relatively similar time-independent
mean frequencies f0i
and different widths
D fi
of their
spectra obtained from sonograms, but approximately the same times
ti
of group delay (except for events 4 and 5). These parameters
for all ten events are listed in Table 1.
Each individual series in the sonogram consists of a number of
structural elements, which are substantially the Pc 1 wave packets.
The analysis of the dynamical spectra of ten Pc 1 events in the
sonograms have shown that the difference between the mean
frequencies of a series in each event is
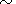 0.2-0.5 Hz, and the
spectral width of the individual series
D fi
is 0.05-0.2 Hz.
The lifetimes of individual series differ.
0.2-0.5 Hz, and the
spectral width of the individual series
D fi
is 0.05-0.2 Hz.
The lifetimes of individual series differ.
The solution of the inverse problem of ionospheric modeling is
described by Prikner and Fligel [1991, 1992,
1993] based on
calculated characteristics of the ionospheric filter: the
coefficient of reflection R
and transmission j
on both boundaries of the ionosphere. The dipole magnetic field and
variations of the height characteristics of the base models of
ionosphere were taken into account. This method is outlined by
Prikner and Vagner [1983]. It was assumed that incident on the
irregular, anisotropic, and absorbing thin-layer ionosphere are
left-polarized waves with a frequency
f
and a wave vector oriented
in the magnetic meridian plane at an angle
b
to the ionospheric
boundary. Calculations performed by the method described by
Prikner and Vagner [1983] yield R
and j:
|
R(b, f) = Arefl / Ainc , j(b, f) = Aprop / Atot
| (1) |
where Arefl
is the amplitude of the wave reflected from the
ionosphere, Ainc
is the amplitude of the incident wave,
Aprop
is the amplitude of the wave that has propagated to the Earth's
surface, and
Atot
is the sum of the incident wave and the wave
reflected from the ionosphere.
As is shown by Belyakov et al. [1983],
Ostapenko and Polyakov
[1990],
Prikner and Vagner [1983, 1990], and
Rudenko [1990], the
frequency dependencies
R(f)
and
j(f)
at a prescribed
incidence angle
b
have an oscillatory structure with several
peaks arranged more or less regularly and characterize the
resonator at its two boundaries. The frequency arrangement of the
peaks depends on the main characteristic of the resonator: the
electron density vertical profile
Ne(Z), which also determines the
attenuation of waves in the resonator. With regard to the height
profiles
ne(Z),
ni(Z), and
mi(Z), where
ne and
ni are
the effective collision frequencies of the charged particles and
mi is the effective ion mass,
these do affect the values of R(f)
and j(f)
, but not the frequency arrangement of their
resonance peaks.
In this work we are only interested in the frequency arrangement of
the resonance peaks of
R(f)
and
j(f), and not in their
absolute values; therefore the choice of the height profiles
ne,
ni, and
mi will not be discussed.
 In modeling the resonator characteristics (1), the choice of the
ionospheric model is essential. For auroral geomagnetic latitudes,
models for the cases of low and high solar activity were used.
Vertical profiles of
Ne,
ne, and
ni for some models are
shown in Figure 1 for heights of 200-3000 km. Models DL and
NL are for daytime and nighttime conditions, respectively, and
characterize the ionosphere under low solar activity
( F10.7 = 70 ),
whereas models DH and NH describe the daytime and nighttime
ionosphere under high solar activity ( F10.7 = 200 ).
We will call these the base models. The distribution of
Ne(Z)
in the lowest
ionosphere at
Z
In modeling the resonator characteristics (1), the choice of the
ionospheric model is essential. For auroral geomagnetic latitudes,
models for the cases of low and high solar activity were used.
Vertical profiles of
Ne,
ne, and
ni for some models are
shown in Figure 1 for heights of 200-3000 km. Models DL and
NL are for daytime and nighttime conditions, respectively, and
characterize the ionosphere under low solar activity
( F10.7 = 70 ),
whereas models DH and NH describe the daytime and nighttime
ionosphere under high solar activity ( F10.7 = 200 ).
We will call these the base models. The distribution of
Ne(Z)
in the lowest
ionosphere at
Z 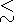 200 km is the same as reported by
Prikner [1986]. We also used an auxiliary model
DM constructed for the mean
physical parameters of the ionosphere, i.e., for average (over
solar activity) distributions of the temperature
Te,
Ti, and
Tn,
densities Ne and Nn,
and ion masses mi
according to Prikner
[1986].
200 km is the same as reported by
Prikner [1986]. We also used an auxiliary model
DM constructed for the mean
physical parameters of the ionosphere, i.e., for average (over
solar activity) distributions of the temperature
Te,
Ti, and
Tn,
densities Ne and Nn,
and ion masses mi
according to Prikner
[1986].
To determine the Ne
with an arrangement of peaks of the
R(f)
coefficients which is closest to the experiment, we used three
types of variations of the vertical profiles of
Ne at altitudes
Z> 200 km with the base models DL, DH, NL, NH and DM
[ Prikner and Fligel, 1993].
In type I the distributions of
Ne(Z)
in the base models DL and NL
varied as follows. It was assumed that the maximum increase in
Ne(%)
relative to the base model, i.e., the value of
pNe(%)
occurs at an altitude of
Z 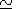 300 km, and then
pNe decreases
with height and disappears at Z 1500 km, i.e., the changed
profile of Ne(Z) at
Z 1500 km coincides with the base profile.
300 km, and then
pNe decreases
with height and disappears at Z 1500 km, i.e., the changed
profile of Ne(Z) at
Z 1500 km coincides with the base profile.
In type II the decrease in density at altitudes
Z 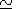 300-500 km
( pNe < 0 )
and its slight increase at altitudes
Z
300-500 km
( pNe < 0 )
and its slight increase at altitudes
Z 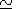 1000-1200 km was
considered. This variation may be determined by
"heating" of the neutral component of plasma because of friction
with the accelerated ions
[ Sellek et al., 1991]. The effect
disappears at altitudes
Z
1000-1200 km was
considered. This variation may be determined by
"heating" of the neutral component of plasma because of friction
with the accelerated ions
[ Sellek et al., 1991]. The effect
disappears at altitudes
Z 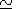 1500 km.
1500 km.
For type III both positive and negative variations of
Ne with a
constant value of pNe(%)
along the entire profile were considered.
The increase in
Ne in models DL and NL was assumed up to the
values of Ne in models DH and NH.
The frequency distribution of the peaks of
R(f)
also depends on the
choice of the angle of incidence of waves onto the ionosphere
[ Prikner and Fligel, 1992;
Prikner and Vagner, 1983, 1988]. For the
Kerguelen, Sogra, and Nurmijarvi observatories, values
b = 68, 70, and 73o
were selected. Values b = 68 and
70o suited
the experimental conditions best of all. Since the Pc 1 wave
envelopes propagate in the form of left-handed waves along the
field lines, their angle ( b )
of incidence onto the ionosphere
is determined by the angle of entry of the field lines into the
ionosphere.
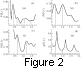 Figure 2a shows the results of modeling event 4 (April 22, 1965,
0220 UT, Kerguelen observatory). The most suitable was the
ionospheric model DL using type I variations with
pNe = 100%,
b = 70%. The peaks of
R(f) are seen to agree well with the
experiment (vertical lines). The third series of this event with a
mean frequency
f
Figure 2a shows the results of modeling event 4 (April 22, 1965,
0220 UT, Kerguelen observatory). The most suitable was the
ionospheric model DL using type I variations with
pNe = 100%,
b = 70%. The peaks of
R(f) are seen to agree well with the
experiment (vertical lines). The third series of this event with a
mean frequency
f 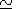 1.1 Hz is found in the center
of the twin maximum of
R(f). Another example of good agreement of the modeling
results with the experiment is shown in Figure 2b for event 9
(Kerguelen, March 30, 1966, 2230 UT), where the nighttime model NL
with type III variations,
pNe = -30% and
b = 68%, is used. The
Pc 1 series with central frequencies of 0.58 and 1.0 Hz agrees well
with the
R(f)
peaks. Figure 2c shows the calculation results for
event 1 (Kerguelen, April 6, 1964, 0800 UT). For this event, good
agreement was obtained using a model with type III variations and
pNe = 40%.
The calculations of the transmission function are shown
in Figure 2d with the clearly seen sharp peaks of the resonance
variation of the
j(f)
coefficient with a very weak
attenuation of the wave amplitude.
1.1 Hz is found in the center
of the twin maximum of
R(f). Another example of good agreement of the modeling
results with the experiment is shown in Figure 2b for event 9
(Kerguelen, March 30, 1966, 2230 UT), where the nighttime model NL
with type III variations,
pNe = -30% and
b = 68%, is used. The
Pc 1 series with central frequencies of 0.58 and 1.0 Hz agrees well
with the
R(f)
peaks. Figure 2c shows the calculation results for
event 1 (Kerguelen, April 6, 1964, 0800 UT). For this event, good
agreement was obtained using a model with type III variations and
pNe = 40%.
The calculations of the transmission function are shown
in Figure 2d with the clearly seen sharp peaks of the resonance
variation of the
j(f)
coefficient with a very weak
attenuation of the wave amplitude.
 Figure 3 shows the height profiles
Ne(Z)
calculated for the same
events 1, 4, and 9. These profiles are used in the calculations
shown in Figure 2. Figure 3 compares these with the base models of
Ne(Z)
shown as solid lines. Fitting of the obtained profiles to the
Ne(Z) profiles at
Z < 300 km was carried out in the same way
as Belyaev et al. [1990b] did for models D5L and N5L.
Figure 3 shows the height profiles
Ne(Z)
calculated for the same
events 1, 4, and 9. These profiles are used in the calculations
shown in Figure 2. Figure 3 compares these with the base models of
Ne(Z)
shown as solid lines. Fitting of the obtained profiles to the
Ne(Z) profiles at
Z < 300 km was carried out in the same way
as Belyaev et al. [1990b] did for models D5L and N5L.
The modeling results for all the events are listed in Table 2,
where
f0i
are the values of mean frequencies for the
R(f)
peaks.
For all the events, except event 10, the models for low solar
activity proved to be the most suitable for the experimental
conditions. This is not just accidental, since the low geomagnetic
activity in all the events considered is confirmed by the low
values of the indices
Kp 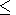 | 20 |
and
Ap
| 20 |
and
Ap 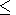 6. For
event 10, model DM proved to be the most suitable, but with
somewhat decreased values of Ne
over the entire profile.
6. For
event 10, model DM proved to be the most suitable, but with
somewhat decreased values of Ne
over the entire profile.
Discussion
For comparatively long series of the "pearls" with a constant
central frequency corresponding to a maximum signal amplitude to
exist, there must be relatively stable properties of both the
source of amplification and the conditions of propagation in the
flux tube and reflection of signals in the conjugate hemispheres
during the entire time of recording. One indirect evidence of such
stable conditions may be the low values of the Kp
and Ap
indices
in all the events in question. Besides, a condition for the
appearance and persistence of such a series of "pearls" is the
practical coincidence of the reflection characteristics in the
conjugate hemispheres (at least in the frequency intervals of the
Pc 1 series). The assumption of similar reflection characteristics
of waves in the conjugate hemispheres during the duration of the
series of "pearls" with a time-constant central frequency is
evidenced by the very fact of the existence of the discussed
pulsation events. Incoherence of the reflection coefficients in
frequency in the conjugate hemispheres may result in both the
impossibility of a multiple amplification process (reflection in
the Alfvén maser in general) and, for example, the occurrence of
different shifts of the central frequency. Such events of the
"pearls" do occur, but these are beyond the scope of the present
paper.
Analysis of the frequency components obtained in the modeling has
shown their good agreement with the observed frequencies of the
series for all the Pc 1 events under study, except in events 5 and
10 (see the numerals in parentheses in Table 2). For these events,
modeling resulted in occurrence of a frequency component that did
not exist within the interval of the recorded series. Such a
spectral component can disappear upon reflection from a conjugate
ionosphere, if it is absent in the reflection spectrum.
It should be noted that the occurrence of the component
f0i 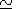 0.5
Hz (
ti
0.5
Hz (
ti 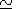 152
s) in event 5 (see Table 1) is of
special interest because this event is beyond the scope of the
hypothesis proposed by Feygin et al. [1994] and
Nekrasov et al.
[1991] that explains the occurrence of simultaneous Pc 1 series and
is corroborated by the present work. In accordance with this
hypothesis, occurrence of simultaneous Pc 1 series is determined by
one source generating a wide Pc 1 spectrum, in which, because of
the resonance character of the reflection coefficient
R(f), only
those frequencies that correspond to the
R(f)
maxima are isolated.
In this context, it is assumed that the repetition periods
ti
of signals in each series of a given event practically coincide. On
the other hand, the values of
ti
in event 5 are 152, 95, and 93 s.
This fact may be related to the assumption that the generation
source itself occupies a wide spatial region extended in the radial
direction; therefore, the generated ion-cyclotron waves come to the
observation point by different paths and have different times of
group delay. A similar situation may take place in event 4 as well.
152
s) in event 5 (see Table 1) is of
special interest because this event is beyond the scope of the
hypothesis proposed by Feygin et al. [1994] and
Nekrasov et al.
[1991] that explains the occurrence of simultaneous Pc 1 series and
is corroborated by the present work. In accordance with this
hypothesis, occurrence of simultaneous Pc 1 series is determined by
one source generating a wide Pc 1 spectrum, in which, because of
the resonance character of the reflection coefficient
R(f), only
those frequencies that correspond to the
R(f)
maxima are isolated.
In this context, it is assumed that the repetition periods
ti
of signals in each series of a given event practically coincide. On
the other hand, the values of
ti
in event 5 are 152, 95, and 93 s.
This fact may be related to the assumption that the generation
source itself occupies a wide spatial region extended in the radial
direction; therefore, the generated ion-cyclotron waves come to the
observation point by different paths and have different times of
group delay. A similar situation may take place in event 4 as well.
Solving of the problem with the aim of determining not only
frequency characteristics but also the amplitude characteristics of
the observed Pc 1 series would be far harder, since this would
require consideration of the ionospheric temperature
characteristics
Te(Z),
Ti(Z),
Tn(Z) and also the dependencies of
ne(Z)
and ni(Z).
Consideration of these is especially important
in the lowest ionosphere (up to the maximum of the
F2
layer), where
these exert strong influence on wave attenuation, thereby affecting
the amplitude of the reflection and transmission coefficients.
If one assumes that the
Ne(Z)
vertical profiles can be obtained by
the comparatively simple method described above, then, by varying
the ne(Z)
and
ni(Z)
vertical profiles, one can obtain the
transmission coefficients
j(b, f)
. This, in turn, will
make it possible to determine the ratio of pulsation amplitudes on
both boundaries of the ionospheric layer. And, approximate as the
obtained results may be, this still would enlarge applications of
the method of numerical simulation of ionospheric filtration of the
Pc 1 range signals.
Conclusions
Electron density vertical profiles
Ne(Z)
of the ionospheric Alfvén
resonator are determined from ground-based observations of
simultaneous series of the Pc 1 geomagnetic pulsations. The
obtained
Ne(Z)
profiles agree quite well with the known
Ne(Z)
models of the ionosphere for low solar activity, which also agrees
with the conditions of the experiment (low
Kp
indices).
Acknowledgments
The authors thank P. P. Belyaev for helpful
discussion. One of the author (F. Z. F.) acknowledges the support
of the Russian Foundation for Basic Research via projects
97-05-65404 and 97-05-64606 and Department of Sciences of Russian
Government via Research Project "Arktika".
References
Belyaev, P. P., S. V. Polyakov, V. O. Rapoport, and V. Yu.
Trakhtengerts, On the small-scale structure of the Alfvén maser,
Geomagn. Aeron., 24, 242, 1984.
Belyaev, P. P., S. V. Polyakov, V. O. Rapoport, and V. Yu.
Trakhtengerts, Peculiarities of wave generation in a nonsymmetric
Alfvén maser,
Geomagn. Aeron., 25, 603, 1985.
Belyaev, P. P., S. V. Polyakov, V. O. Rapoport, and V. Yu.
Trakhtengerts, Formation of dynamical spectra of the Pc 1
geomagnetic pulsations,
Geomagn. Aeron., 27, 652, 1987.
Belyaev, P. P., S. V. Polyakov, V. O. Rapoport, and V. Yu.
Trakhtengerts, Linear theory of small-scale structure of the
frequency-drift Alfvén maser emission,
Radiofizika, 4, 408, 1990a.
Belyaev, P. P., S. V. Polyakov, V. O. Rapoport, and V. Yu.
Trakhtengerts, The ionospheric Alfvén resonator,
J. Atmos. Terr. Phys., 52 (9), 781, 1990b.
Belyakov, S. V., V. O. Rapoport, and V. Yu. Trakhtengerts, Alfvén
swept-signal maser, Fiz. Plazmy, 9 (2), 371, 1983.
Feygin, F. Z., and V. L. Yakimenko, On the small-scale type Pc 1
micropulsation structure,
Geomagn. Aeron., 10, 558, 1970.
Feygin, F. Z., et al., Coherent multiple Pc 1 pulsation bands:
Possible evidence for the ionospheric Alfvén resonator,
Ann. Geophys., 12, 147, 1994.
Gendrin, R., et al., Wave packet propagation in the amplifying
medium and its application to the dispersion characteristics and to
the generation mechanisms of Pc 1 events,
Planet. Space Sci., 19, 165, 1971.
Lysak, R. L., Theory of auroral zone Pi B pulsation spectra,
J. Geophys. Res., 93, 5942, 1988.
Nekrasov, A. K., et al., On the effect of the ionosphere on the
spectral structure of the Pc 1 geomagnetic pulsations,
Geomagn. Aeron., 31, 607, 1991.
Ostapenko, A. A., and S. V. Polyakov, Dynamics of the coefficient
of reflection of Pc 1 Alfvén waves from the ionosphere during
variations of electron density of the lower ionosphere,
Geomagn. Aeron., 30, 50, 1990.
Polyakov, S. V., and V. O. Rapoport, The ionospheric Alfvén
resonator, Geomagn. Aeron., 21, 816, 1981.
Prikner, K., The ionosphere of the higher geomagnetic latitudes
( L = 3 and L = 5 ) as an ULF filter,
Stud. Geophys. Geod., 30, 304,
1986.
Prikner, K., and D. S. Fligel, Rapid changes of the outer
high-latitude ionosphere combined with a penetration of intensive
ULF (Pc 1) signals,
Planet. Space Sci., 39, 1657, 1991.
Prikner, K., and D. S. Fligel, Application of the method of
numerical simulation of ionospheric filtration of Pc 1 signals to
solving the inverse problem of ionospheric modelling,
Stud. Geophys. Geod., 36, 240, 1992.
Prikner, K., and D. S. Fligel, Conjugate ground-satellite
measurements of Pc 1 signals and their application to wave
diagnostic of the high-latitude outer ionosphere,
Ann. Geophys., 11, 897, 1993.
Prikner, K., and V. Vagner, Numerical modelling of the ionospheric
filtration of the ULF micropulsation signal,
Stud. Geophys. Geod., 27, 173, 1983.
Prikner, K., and V. Vagner, Changes in the reflectivity of the
midlatitude ionosphere with respect to the ULF (Pc 1) signal,
Stud. Geophys. Geod., 32, 84, 1988.
Prikner, K., and V. Vagner, The ionosphere as an Alfvén resonator
in the Pc 1 micropulsation range, Stud. Geophys. Geod., 35, 342,
1990.
Rudenko, G. V., Numerical study of the Alfvén resonance in the
ionosphere, Radiofizika, 33, 155, 1990.
Sellek, R., et al., Effects of large zonal plasma drifts on the
subauroral ionosphere, J. Atmos. Terr. Phys., 53, 557, 1991.
Load file for printing and local use.
This document was generated by TeXWeb (Win32, v.1.0) on December 12, 1997.
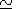 0.2-5
Hz) geomagnetic
pulsations ("pearls"). The mechanism is based on solving the
self-consistent problem of the interaction of Alfvén waves with hot
anisotropic protons on field lines with footpoints in conjugate
ionospheres. Using the "realistic" properties of the medium, the
aforesaid authors were able to explain the formation of the
structured emission, a long-standing mystery in the theory of
generation of the "pearls". These authors considered the
quasi-linear interaction of Alfvén waves with hot anisotropic
protons and precipitation of the latter into the ionosphere
(ensuring the auxiliary ionization), which led them to interpret
the fine effects of the dynamical spectrum of the "pearls"
differently from the mechanism earlier proposed by
Feygin and Yakimenko [1970] and
Gendrin et al. [1971].
0.2-5
Hz) geomagnetic
pulsations ("pearls"). The mechanism is based on solving the
self-consistent problem of the interaction of Alfvén waves with hot
anisotropic protons on field lines with footpoints in conjugate
ionospheres. Using the "realistic" properties of the medium, the
aforesaid authors were able to explain the formation of the
structured emission, a long-standing mystery in the theory of
generation of the "pearls". These authors considered the
quasi-linear interaction of Alfvén waves with hot anisotropic
protons and precipitation of the latter into the ionosphere
(ensuring the auxiliary ionization), which led them to interpret
the fine effects of the dynamical spectrum of the "pearls"
differently from the mechanism earlier proposed by
Feygin and Yakimenko [1970] and
Gendrin et al. [1971].
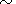 0.2-0.5 Hz, and the
spectral width of the individual series
D fi
is 0.05-0.2 Hz.
The lifetimes of individual series differ.
0.2-0.5 Hz, and the
spectral width of the individual series
D fi
is 0.05-0.2 Hz.
The lifetimes of individual series differ.
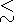 200 km is the same as reported by
Prikner [
200 km is the same as reported by
Prikner [

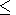 | 20 |
and
Ap
| 20 |
and
Ap