A. I. Semenov and N. N. Shefov
Institute of Atmospheric Physics, Moscow, Russia
The hydroxyl emission is one of the most energetically important in the upper atmosphere. It manifests the recombination process of atomic oxygen. An essential feature of this emission is the possibility of reliably registering its spectral and aeronomical parameters, which characterize not only the processes of hydroxyl radical excitation, but also properties and state of the atmosphere where it is generated. Such parameters are: the intensity Iv'v'' (in Rayleigh) of particular molecular bands (v',v''), the equilibrium Te and nonequilibrium Tne rotational temperatures, which describe a distribution of the OH excited molecules over the rotational states (J, N), the vibrational temperature TV, which characterizes a distribution of the OH molecules over the vibrational states v and the related photochemical processes. All these parameters correspond to the height zm of the maximum of the emitting layer, which has the emission measure Qm (photons cm -3 s -1 ), and the layer thickness W, which is determined at the Qm/2 level. According to the above definition the total intensity of the hydroxyl emission, which characterizes the rates of energy transformation and loss, is
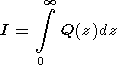 |
Studies of the hydroxyl emission have been carried out during the past 45 years, though rather irregularly (in time and planetary distribution) from the point of view of data accumulation on various emission parameters. The latter fact creates difficulties in searches for particular types of variations. Nevertheless, these data are obviously needed, because the observed temporal and spatial variations manifest a whole spectrum of photochemical and dynamical processes in the atmosphere.
The detailed photochemistry of formation of the hydroxyl emission in the atmosphere is rather complicated and depends on a large number of geophysical conditions. However, ozone, atomic oxygen, atomic hydrogen, and the solar UV radiation are the principal components, which determine generation of the emission. Temporal and spatial behavior of the above parameters in the mesopause region may be studied on the basis of the hydroxyl emission data, so we have tried to systematize the observational results, accumulated for many years. It should be emphasized that the data available cover only the nighttime periods. There are only episodical measurements for the daytime, which are not enough for any kind of systematization.
Considering the problem of creation of the model of emission behavior one has to keep in mind a very broad spectrum of variations, which contains both regular and irregular components. The values of the regular variations can be calculated for a fixed time and place, whereas the irregular variations may begin at a moment determined by occasional events, but their behavior after the beginning is of a regular character.
There have been numerous attempts to systematize various particular types of measurements (the intensity I, and the rotational Tr and vibrational TV temperatures) to get some general ideas concerning the hydroxyl emission behavior [Fishkova, 1983; Semenov and Shefov, 1979; Shefov, 1969, 1971, 1976; Shefov and Piterskaya, 1984; Toroshelidze, 1991].
Insofar as all the variations are in fact a modulation of some average value of the hydroxyl emission characteristics, the following form of representation of the Tr, TV, and zm parameters of the hydroxyl emission was accepted as a first approximation:
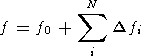 |
The first approximation for the emission intensity is
 |
where
f0 are some global mean values for the given solar and
geophysical conditions, in particular, geographic latitude is
j= 45 o N; geographic longitude is
l 40 o
E; local time
is the local solar midnight,
t = 0 ; season is the equinox, day
of the year is
td = 80, solar activity is
F10.7 = 130 ;
geomagnetic activity is
Kp = 0 ; the year is 1972.5.
40 o
E; local time
is the local solar midnight,
t = 0 ; season is the equinox, day
of the year is
td = 80, solar activity is
F10.7 = 130 ;
geomagnetic activity is
Kp = 0 ; the year is 1972.5.
Thus, due to a limited amount of data at the present stage it is suggested that the OH emission behavior in the northern and southern hemispheres is the same, and the longitudinal variations are governed only by the local time.
The Dfi values describe variations of different types: First, the regular variations are as follows: Dfd (c, j) are the diurnal variations during the night, c and j being the solar zenith angle and latitude, respectively; Dfte(t) are the terminator variations in the morning and evening hours, t being the local time; DfL (tLA) are the lunar variations during a synodical month (29.53 days), tLA being the lunar phase; Dfs (td) are the seasonal variations, td being the day of the year; Dfqbo(tqbo) are the quasi-biennial variations with a period of 22-32 months, tqbo being the year of the beginning of the quasi-biennial cycle; Df5.5(t5.5) are the 5.5-year variations, t5.5 being the year of the beginning of the cycle; DfF (F10.7) are the solar cycle variations, F10.7 being the solar radio emission flux (the 22-year variations are accounted for by the F10.7 index); Dftr(ttr) is the long-term trend, ttr being the year of the beginning of the trend count; Dfj (j) are the latitudinal variations; Dfor (V, L) are the orography variations, V and L being the wind velocity in the troposphere and the distance to the mountain, respectively;
Second, the irregular variations are as follows: Df27 (t27) are the 27-day variations, induced by variations of the solar activity and UV radiation, t27 being the date of the beginning of the nearest Carrington cycle; Dfsw (tsw) are the variations after stratospheric warmings, tsw being the date of the warming beginning; Dfgm (tgm, Kp, F) are the variations after geomagnetic disturbances, tgm, Kp and F being the date of the beginning of a geomagnetic storm, the planetary geomagnetic index, and the geomagnetic latitude, respectively; Dfmf (tmf) are the variations after meteor flux intrusion, tmf being the date of the intrusion beginning; Dfgw (tw) are the variations due to the internal gravity waves, tw being the wave period.
It is widely known that the hydroxyl emission, generated in the
mesopause region (~87 km), is due to the rotational-vibrational
transitions ( v' = 9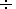 1,
v'' = (v' - 1)
1,
v'' = (v' - 1)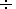 0) of the ground
electronic
state
X2P. Its total intensity is a
sum of the intensity
Iv'v'' of the bands situated in the 0.5-5.0
m m spectral
region. Among them the sequence
Dv = 2 in the 1.4-2.2
m m
spectral range has the highest intensity (in photons)
[Shefov and Piterskaya, 1984].
0) of the ground
electronic
state
X2P. Its total intensity is a
sum of the intensity
Iv'v'' of the bands situated in the 0.5-5.0
m m spectral
region. Among them the sequence
Dv = 2 in the 1.4-2.2
m m
spectral range has the highest intensity (in photons)
[Shefov and Piterskaya, 1984].
On average the distribution of the population of the
vibrational levels may be described by the Boltzmann distribution
with the vibrational temperature
TV 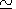 10,000 K, though
there
are indications of the existence of two pieces of the distribution
at
v = 1
10,000 K, though
there
are indications of the existence of two pieces of the distribution
at
v = 1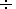 5 and
v = 6
5 and
v = 6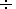 9, for which
T6789
9, for which
T6789 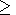 T12345
[Fishkova, 1981, 1983;
Shefov, 1976;
Turnbull and Lowe, 1983].
Thus, the total emission intensity (in photons) is
T12345
[Fishkova, 1981, 1983;
Shefov, 1976;
Turnbull and Lowe, 1983].
Thus, the total emission intensity (in photons) is
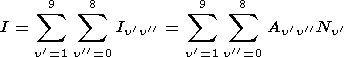 |
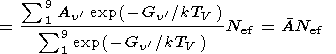 |
where Av'v'' are the transition probabilities and Nv' are the populations of the v' vibrational levels. The latest values of Av'v'' are given by Nelson et al. [1990] and Turnbull and Lowe [1989]. Table 1 shows for each (v',v'') band the average values of Av'v'', based on the data of Nelson et al. [1990]. It should be emphasized here that the use of the data of nonsimultaneous measurements of some OH bands, presented by Krassovsky et al. [1962] but not reduced to some standard conditions, was a defect of many papers on calculation of the transition probabilities, so further specification of the Av'v'' values is needed. Vibrational level energies Gv (in cm-1 ) are determined by the relation
where k is the Boltzmann constant; Nef is the effective number (cm-2 ) of the OH excited molecules; A (Tv) (~48 s-1 for TV = 10,000 K) is the effective transition probability. The approximation has the form
 2
2
 3 - 0.0587 T
3 - 0.0587 T 4
4 where T' = TV/10,000.
From that the intensity (in photons) of a particular OH bands is
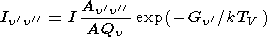 |
where the sum over the vibrational states is
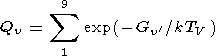 |
and its approximation looks like
 2 +
2 +
 3 - 0.345 T
3 - 0.345 T 4
4 The total energy of the hydroxyl emission is equal to:
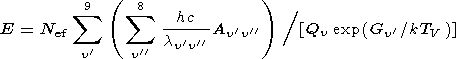 |
or
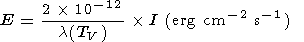 |
where lv'v'' is the wavelength of the OH bands. The effective wavelength (in m m) is
 2 - 1.051
T
2 - 1.051
T 3 + 0.165 T
3 + 0.165 T 4
4
The OH rotational (equilibrium) temperature Tr is determined by the distribution of the first four- to five lines of the P branch of the rotational structure of the band [Shefov, 1961]. Information on transition probabilities for various lines of the branch may be found in the work by Krassovsky et al. [1962]. The measured value of Tr is the weighted mean of the atmospheric temperatures T inside the emitting layer. This value practically corresponds to the altitude of the layer maximum emission measure Qm. However, there is a dependence of Tr on the v number [Fishkova, 1983; Lowe et al., 1991; Shefov, 1961, 1972, 1976; Shefov and Piterskaya, 1984], which is due to some differences in the altitudes zmv of the layers corresponding to different v [Baker and Stair, 1988; Potapov et al., 1983]. The average empirical dependence has the form
Later on, all the data on Tr were reduced to the value of v = 5, for which DTrv = 0. Unfortunately, there is no information on possible variations of this value for various solar and geophysical conditions.
The nonequilibrium rotational temperature
Tnr (~1100 K) was
recently revealed on the basis of the intensity distribution of the
lines of the
P branch of the (7.3) 882.4 nm band with the
rotational numbers
N' = 6-12 [Perminov and Semenov, 1992].
A
nonequilibrium and, as a consequence, such high values of the
rotational temperature are due to incompleteness of the processes
of vibrational relaxation for high
N in the upper part of the
emitting layer. In satellite measurements the transitions for
N' 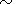 33 were reported
[Dodd et al., 1993],
as well as pure
rotational transitions in the 10-25
m m spectral range, which
occur between high rotational levels
[Dodd et al., 1994].
33 were reported
[Dodd et al., 1993],
as well as pure
rotational transitions in the 10-25
m m spectral range, which
occur between high rotational levels
[Dodd et al., 1994].
Diurnal variations of Tnr are synchronous to the variations of the vibrational temperature and exhibit changes in altitude of the upper part of the OH emitting layer. On the basis of a small amount of data at the Zvenigorod observatory ( j = 57 o N is the latitude of the observed region of the emitting layer) the variations at night near equinoxes are described by the relation
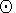
The lunar-tide variations in the plane of the lunar orbit are
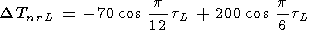 |
where tL is the lunar time.
The shape of the emission vertical profile until recently has been studied only by rocket methods. The measurements by the UARS satellite were started in 1991 [Lowe and LeBlanc, 1993], but the results have not yet been published. Currently 44 rocket measurements conducted from 1956 to 1992 are known [Baker and Stair, 1988; Shefov and Toroshelidze, 1975], out of which only about 30-35 flights can be analyzed. In these data the most uncertain parameter is the shape of the vertical profile. Theoretical studies point to an asymmetry of the profile, in which the upper part (above the height of maximum zm ) is thicker than the lower part (below zm ) [Moreels et al., 1977].
In that case the shape of the vertical profile of the emission measure may be presented in the form
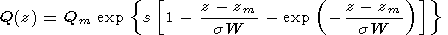 |
where Qm =[ss e-s/G (s)](I/sW), W corresponds to the layer thickness at the Qm/2 level, s and s are parameters, G (s) is the Gamma function. Then
 |
The asymmetry index P of the profile, which characterizes the portion on the thickness of the upper part of the layer, is determined by the relations:
and
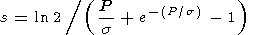 |
However, rocket measurements, because of difficulties in taking
into account correct orientation of the rocket and also, apparently
due to a significant inhomogeneity of the emitting layer, which is
created by various disturbances, point to a practically symmetric
vertical distribution with thickness
W. This was
demonstrated by several examples of the most successful
measurements
[Shefov, 1978a].
Special studies on board the UARS
satellite point to a presence of the asymmetry ( P 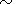 0.65 )
[Lowe and LeBlanc, 1993].
Nevertheless, while registering the
vertical profile of the emitting layer intensity, which is observed
along the tangent line along the limb, solution of the inverse
problem of reconstruction of the shape of the emitting layer lower
part presents some difficulties, because it requires a preliminary
knowledge of the required function
[Shefov, 1978a].
At the given
stage of the analysis, a comparison of the simultaneously measured
values of
zm and
W for various flights has shown the presence of a
correlation between them and a distinct splitting into two
subgroups of the vibrational levels: 1-5 and 6-9. Their average
for
v = 4
0.65 )
[Lowe and LeBlanc, 1993].
Nevertheless, while registering the
vertical profile of the emitting layer intensity, which is observed
along the tangent line along the limb, solution of the inverse
problem of reconstruction of the shape of the emitting layer lower
part presents some difficulties, because it requires a preliminary
knowledge of the required function
[Shefov, 1978a].
At the given
stage of the analysis, a comparison of the simultaneously measured
values of
zm and
W for various flights has shown the presence of a
correlation between them and a distinct splitting into two
subgroups of the vibrational levels: 1-5 and 6-9. Their average
for
v = 4
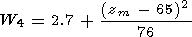 |
and for v = 8
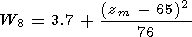 |
The zm altitude dependence on v is also revealed:
That is why while analyzing the data of measurements to obtain various types of variations, all the data were reduced to v = 5. Thus,
If we assume the Gaussian shape of the vertical profile of the emission measure, then
where
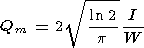 |
To determine the above considered variations, a statistical
systematization of the measurements of the rotational (equilibrium)
and vibrational temperatures at the Zvenigorod observatory and
other stations was performed
[Agashe et al., 1989;
Fishkova, 1955, 1978, 1981,
1983;
Kropotkina, 1976;
Kropotkina and Shefov, 1977;
Kvifte, 1967;
Matveeva and Semenov, 1985;
Megrelishvili and Fishkova, 1986;
Myrab et al., 1983;
Perminov et al., 1993;
Potapov et al., 1983;
Scheer and Reisen, 1990;
Semenov and Shefov, 1979;
Shefov, 1967, 1968, 1969,
1971,
1972, 1973, 1974a,
1974b, 1975,
1976, 1978b;
Shefov and Piterskaya, 1984;
Shefov and Toroshelidze, 1975;
Takahashi et al., 1990;
Taranova and Toroshelidze, 1970;
Toroshelidze, 1968, 1975, 1991;
Turnbull and Lowe, 1991;
Yarin, 1970]
and also of the height
of the emitting layer by rocket and satellite data
[Baker and Stair, 1988;
Lowe and LeBlanc, 1993;
Lowe and Lytle, 1973,
Moreels et al., 1977;
Shefov and Toroshelidze, 1975].
Due to
obvious reasons the entire huge list of the publications cannot be
cited here. In spite of the amount of data available not all the
types of variations can be studied in detail. This is particularly
true
for the data on the altitude of the emitting layer and
vibrational temperature. So in determination of variations in
cases where there were not enough data available, a knowledge
of the behavior of
other parameters was useful, because variations of various
parameters were interrelated. On the basis of the performed
systematization the following characteristics of the hydroxyl
emission for the above indicated solar and geophysical conditions
were obtained:
Tr0 = 195 K;
I0 = 0.95 MR,
Qm0 = 1.1 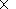 106 photon cm
-3 s
-1 ;
TV0 = 10,000 K;
E0 = 1 erg cm
-2 s
-1 ;
zm0 = 87 km;
W0 = 9 km;
A = 48 s
-1 ;
l = 1.9 m m.
106 photon cm
-3 s
-1 ;
TV0 = 10,000 K;
E0 = 1 erg cm
-2 s
-1 ;
zm0 = 87 km;
W0 = 9 km;
A = 48 s
-1 ;
l = 1.9 m m.



 Different types of variations of the considered parameters are
presented in Figures 1,
2,
3,
and 4. In the figures showing variations of
Tr,
I, and
TV the points are the averaged values of these
parameters, and in the figure showing
zm the points are individual
values. During recent years, it has become evident that the
variations of the vibrational temperature
TV (as well as of the
nonequilibrium rotational temperature
Tnr ) exhibit variations of
the atmospheric density
n inside the emitting layer when the
zm altitude is changing
[Perminov and Semenov, 1992;
Perminov et al., 1993;
Shefov, 1978a].
The emission intensity
I and the rotational
temperature
Tr are also changing when the altitude of emission
layer is changing. Thus, empirical approximations of the OH
emission behavior for the conditions of rocket measurements
[Baker and Stair, 1988;
Shefov and Toroshelidze, 1975]
and comparison with
the data of the rocket measurements of
zm reduced to the value of
v=5, provide some control of correctness of the obtained relations.
These results are also presented in
Figures 2,
3,
and 4. The regression
lines look like
Different types of variations of the considered parameters are
presented in Figures 1,
2,
3,
and 4. In the figures showing variations of
Tr,
I, and
TV the points are the averaged values of these
parameters, and in the figure showing
zm the points are individual
values. During recent years, it has become evident that the
variations of the vibrational temperature
TV (as well as of the
nonequilibrium rotational temperature
Tnr ) exhibit variations of
the atmospheric density
n inside the emitting layer when the
zm altitude is changing
[Perminov and Semenov, 1992;
Perminov et al., 1993;
Shefov, 1978a].
The emission intensity
I and the rotational
temperature
Tr are also changing when the altitude of emission
layer is changing. Thus, empirical approximations of the OH
emission behavior for the conditions of rocket measurements
[Baker and Stair, 1988;
Shefov and Toroshelidze, 1975]
and comparison with
the data of the rocket measurements of
zm reduced to the value of
v=5, provide some control of correctness of the obtained relations.
These results are also presented in
Figures 2,
3,
and 4. The regression
lines look like
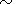 0.74)
0.74)
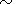 -0.64)
-0.64)
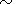 -0.63)
-0.63)
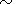 0.77)
0.77)
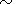 -0.51)
-0.51)
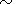 -0.58)
-0.58)
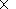 10-11
10-11 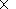 n0.8]
n0.8] where n (in cm -3 ) is a function of zm.
It should be noted that the character of the variations between the hydroxyl emission parameters obtained in rocket measurements for a broad range of solar and geophysical conditions agrees well with the results of measurements at various stations [Agashe et al., 1989; Fishkova, 1955, 1981, 1983; Scheer and Reisen, 1990; Shefov, 1975; Shefov and Toroshelidze, 1975; Takahashi et al., 1990; Toroshelidze, 1991]. It follows from the above presented relations that for regular nighttime variations
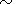 1000 K km-1
1000 K km-1
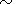 -10 K km-1
-10 K km-1
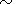 -25% km-1
-25% km-1
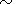 -19% (1000 K)-1
-19% (1000 K)-1
The empirical relations for various types of hydroxyl emission variations are presented below.
1. Variations in the nighttime period of the day are given by
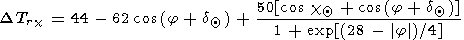 |
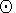 = sin j sin d
= sin j sin d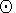 - cos j
cos dc
cos t
- cos j
cos dc
cos t where t is the local mean solar time, and d is the solar inclination angle.
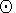 |-0.33
- | cos (j + d
|-0.33
- | cos (j + d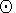 ) |-0.33]
) |-0.33]
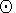 |0.2 - | cos (j +
d
|0.2 - | cos (j +
d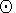 )
|0.2]
)
|0.2]
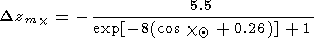 |
The mean behavior at night is based on the data of some publications e.g., [Agashe et al., 1989; Baker and Stair, 1988; Fishkova, 1955, 1981, 1983; Moreels et al., 1977; Myrab et al., 1983; Potapov et al., 1983; Scheer and Reisen, 1990; Shefov, 1971, 1972; Shefov and Toroshelidze, 1975; Takahashi et al., 1990; Toroshelidze, 1975, 1991; Turnbull and Lowe, 1991]. There is no doubt that variations of the hydroxyl emission parameters during the night influence the phase shifts of the thermal semidiurnal tide because of variations of the emitting layer height [Petitdidier and Teitelbaum, 1977; Takahashi et al., 1984] and also the disturbances initiated by propagation of the internal gravity waves (IGW).
Special measurements of the OH emission variations during the
evening and morning twilights at
c = 98-108o were carried out
[Lowe and Lytle, 1973;
Moreels et al., 1977;
Scheer and Reisen, 1990;
Taranova and Toroshelidze, 1970;
Toroshelidze, 1968, 1991;
Turnbull and Lowe, 1991].
Apparently, the observed maxima are
related to the effect of terminator motion
[Toroshelidze, 1991].
Some features of the variations can be studied on the basis of
measurements at summer nights at the latitudes where
c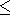 112o
[Shefov, 1971].
For these conditions the periodic (the 4 h and 2 h
harmonics) temperature variations were revealed
[Taranova and Toroshelidze, 1970;
Toroshelidze, 1975, 1991].
At
j
112o
[Shefov, 1971].
For these conditions the periodic (the 4 h and 2 h
harmonics) temperature variations were revealed
[Taranova and Toroshelidze, 1970;
Toroshelidze, 1975, 1991].
At
j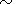 45 o
N
on average in the evening
45 o
N
on average in the evening
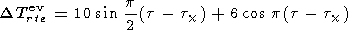 |
where tc is the mean solar time (hours) for c = 98o. That means that the given atmospheric region is at the distance of about 900 km from the terminator.
In the morning time
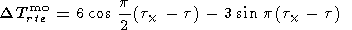 |
However, the data available are not sufficient to describe the behavior of the hydroxyl emission parameters at the 80-100 o solar zenith angles; therefore the above presented formulas are not valid in this region of tc.
2. Lunar variations are given by
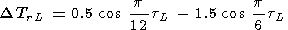 |
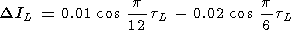 |
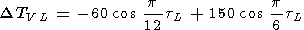 |
The lunar-tide variations during a day have small amplitudes and
are not identified reliably. A representative evaluation was obtained
by
Scheer and Reisen [1990]
on the basis of the data for a durable
observation period. The data on the heights of the emitting layer
are absent. Here
tL is the lunar time in hours.
According to
Chapman and Lindzen [1972]
tL = t
- x, where
x = -0.6173393 + 0.8127167 D ;
D = [( YYYY-1901) 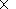 365.25] + 364.5
+ td.
The square brackets in the formula mean the integer part of a
number. YYYY is the year.
365.25] + 364.5
+ td.
The square brackets in the formula mean the integer part of a
number. YYYY is the year.
Variations with lunar age, that is with the synodical month equal to 29.53 days, has higher amplitude than those during a lunar day.
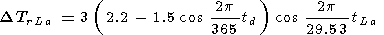 |
 |
 |
 |
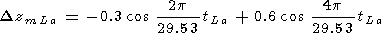 |
The data for DTrLa, DILa, and DTVLa were obtained at the 57o N latitude [Shefov, 1974a, 1974b] and the data on DzmLa were obtained on average at latitudes of 30-40o N, and all the data have been reduced to the plane of the lunar orbit. An approximate evaluation of the lunar age with an accuracy up to several tenths of a day may be made by the formula [Meyes, 1988]:
The square brackets here denote the integer part of a number.
The latitude q and longitude L of the measurement point (relative to the direct line connecting the Earth and Moon centers) of the tide-distorted atmosphere is determined by Chapman and Lindzen [1972] and Kropotkina and Shefov [1977]:
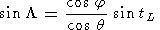 |
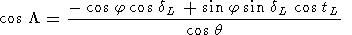 |
where tL and dL are the hourly angle and inclination of the Moon.
The latitudinal distribution of the amplitude of a tidal disturbance of the atmosphere is determined by the relation AL = (1/2)(3 cos2 q -1). In the equatorial system of reference the distribution has the form
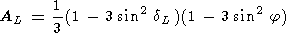 |
The nature of such oscillations in the upper atmosphere is related to the existence in the lower atmosphere of planetary waves [Reshetov, 1973] with periods of about 15 days and 30 days, which are due to parametric excitation of the atmospheric circulation.
3. Seasonal variations are given by
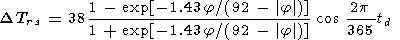 |
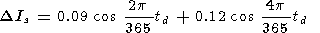 |
 ))0.33 -( cos j)0.33]
))0.33 -( cos j)0.33]
 ))-0.16 -( cos j)-0.16]
))-0.16 -( cos j)-0.16]
 |
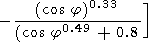 |
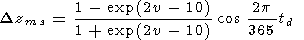 |
The seasonal variations, as well as the diurnal ones, have the highest amplitude among other types of variations [Shefov, 1969]. Their amplitude increases with an increase of latitude. This effect in the initial papers [Kvifte, 1967; Shefov and Yarin, 1962] was explained by the Tr increase with latitude. The character of variations of the Dzms altitude agrees with the data of satellite observations [Hernandez et al., 1995].
4. Quasi-biennial oscillations (QBO) are given by
 |
 |
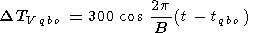 |
According to the middle atmosphere data the quasi-biennial
oscillations have the maximum amplitude in the equatorial zone. The
data in the mesopause region were obtained at the Zvenigorod
observatory
[Shefov, 1973] at
j = 57 o N and at the Abastumani
observatory
[Fishkova, 1983] at
j = 43 o N. The available data
on
zm are not sufficient for description of such variations.
There
is a correlation between the intensity and the zonal wind velocity:
V(W  E)
E)
The
tqbo moments are, for
example, 1960.0 and 1981.1. The moments of cycle beginnings may be
found in the work by
Reid [1994].
Variations of the period of these variations
during 1956-1986 in the limits of 22-23 months were obtained by
Fedorov et al. [1994].
Fedorov et al. [1994]
noted that there is a
pronounced correlation of the
B period with the
F10.7 solar
activity index. An analysis of the experimental data has shown that
the best negative correlation ( -0.76 ) is reached under introduction
of the temporal shift
q between the data, that is,
B(t) = 34.5 - F10.7 (t - q)/22.
Within the limits of the interval of years
available it is approximately true:
q = 2-0.4 cos (2 p
/W)(t-1960), where
W 30-35 years.
30-35 years.
5. The 5.5-year variations are given by
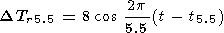 |
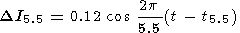 |
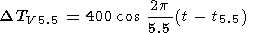 |
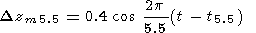 |
These variations occur practically in phase with the 11-year solar activity cycle [Fishkova, 1983; Megrelishvili and Fishkova, 1986; Shefov and Piterskaya, 1984] and so are not well studied. The data on TV were evaluated on the basis of the correlation between the annual mean values of Tr and TV. The moments are t5.5 = 1959.0, 1970.0, 1981.0, and 1992.0.
6. Variations with solar activity level, that is, with the about 11-year period are considered next. We have for the annual mean parameters
The annual mean values of the F10.7 solar radio emission flux with a shift of 0.42 year provide the best correlation (about 0.98) [Semenov and Shefov, 1979; Shefov and Piterskaya, 1984]. The correlations were mentioned by Fishkova [1983], Shefov [1969], Shefov and Piterskaya [1984], and Wiens and Weill [1973].
7. The long-term trend is given by
where t' = (t - 1972.5)/100
The values of the trend were taken relative to 1972.5, because the annual mean value of F10.7 for this year was about 130, which corresponds to the smoothed mean (with the running interval of 22 years) value for the 19-22 solar cycles. The trends are based on the data of Fishkova [1983], Semenov and Fishkova [1995], Shefov [1969], and Shefov and Piterskaya [1984]. It is worth noting that a decrease of the Tr temperature during the solar cycle against the background of the long-term trend is distinctly manifested by an increase of observation frequency of the noctilucent clouds [Gadsden, 1990; Thomas et al., 1989]. The nature of the trend is apparently of a complicated character and manifests both anthropogenic impacts and long-term changes of the solar activity.
8. We next consider latitudinal variations. For the values averaged over a night
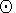 )
)
 |
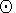 )/50]4}
)/50]4}
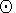 )/28]2 } -500
)/28]2 } -500
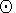 )/50]4}
)/50]4}
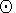 )/28]2 } -0.5
)/28]2 } -0.5
The conclusions of Kvifte [1967] and Shefov and Yarin [1962] on the Tr increase with latitude j are based on the data obtained in winter time. Thus, they manifest the latitudinal dependence of the amplitude of the seasonal variations, but not the behavior of the annual mean values of Tr. The latitudinal variations of DTVj were based on correlation with Dzmj.
9. Disturbed variations after geomagnetic storms are given by
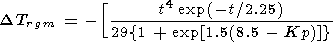 |
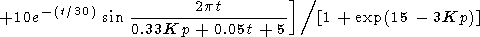 |
where t = tgm - (51- F)/5.4
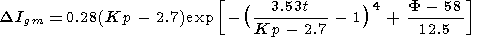 |
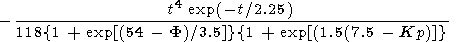 |
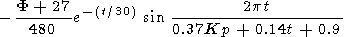 |
where t = tgm - [(52 - F)/9]
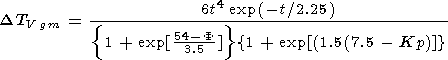 |
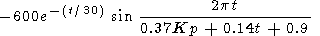 |
where t = tgm - (52 - F)/9 ; Dzmgm = (3- Kp)/12.
The most detailed data were obtained at the Zvenigorod observatory ( F = 51 o N), and the variations are followed down to the equator using the data of several stations [Shefov, 1969; Shefov and Piterskaya, 1984]. A correlation with the ionospheric absorption was revealed [Rapoport, 1983; Shefov, 1978b]. The character of emission behavior points to propagation equatorward from the auroral zone after magnetic storms of composition waves, which transport an additional quantity of water vapor and nitric oxide. The rocket data on zm allow us only to estimate variations of the emission layer height depending on the Kp index at latitudes of about 40-45o N 5-6 days after a geomagnetic disturbance.
10. The 27-day variations are given by
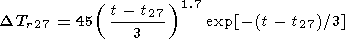 |
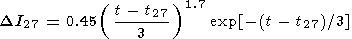 |
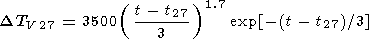 |
This type of variation is related to the Carrington cycles of solar rotation and is evident in the 27-day cycles of solar activity, which lead to UV radiation variations. For this reason the moment of the initial disturbance in the cycle is not constant, but persists on average only during several rotations of the Sun. The variations were considered by Shefov [1967] and Yarin [1970]. There are insufficient rocket data to obtain a picture of Dzm27 behavior.
11. Relation to stratospheric warmings is given by
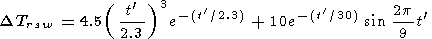 |
where t' = tsw - 5
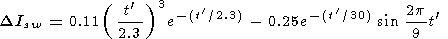 |
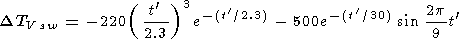 |
The temporal shift of the response of the hydroxyl emission depends on a location of the warming relatively to the place of measurement. According to some measurements not only temperature increase, but a decrease as well was observed [Fishkova, 1978, 1983; Kropotkina, 1976; Matveeva and Semenov, 1985; Shefov, 1973, 1975]. There are not enough rocket data to reveal a Dzmsw behavior.
12. The orographic variations are given by
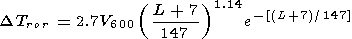 |
This spatial variations of the emission parameters is related to the processes of IGW generation in the vicinity of mountains under interaction with them of the air flow, which has a prevailing wind velocity V600 at the 600 mbar isobaric level. The data for the Caucasus Mountains were presented by Sukhodoev et al. [1989]. The amplitude of the maximum disturbance, its distance from the ridge (its position is schematically denoted by the solid triangle in Figure 1) and spatial dimensions correlate to the wind velocity and are variable depending on the wind azimuth.
13. Variations after intrusion of the meteor fluxes and at the presence of noctilucent clouds are given by
 |
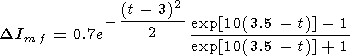 |
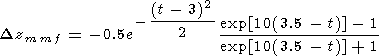 |
The data are based on the observations at the Zvenigorod observatory in summer time. The results indicate to an intensification of the OH emission after meteor flux intrusions (MF in Figures 1, 2, and 4) and during appearance of noctilucent clouds (NC in Figures 1 and 2) [Shefov, 1968]. The mean altitude of the latter is about 82 km [Bronshten and Grishin, 1970]. Distribution of meteor fluxes during a year is presented in Abalakin [1981].
14. The variations due to IGW propagation: is given by
 |
where tw is the wave period (in minutes). Here
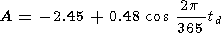 |
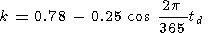 |
This type of variation can not be forecasted during a night, because it is initiated by passage through the mesopause of the IGW generated mainly by meteorological sources in the lower atmosphere [Krassovsky et al., 1977; Semenov and Shefov, 1989]. The location of the sources relative to the place of measurements, and thus the wave period tw, as well as the moments of IGW generation are of an occasional character.
The h parameters, which determine the ratio of relative amplitudes of variations of the intensity and temperature of the OH emission induced by IGW passage through the emitting layer, are different for the upper and lower vibrational levels v [Shagaev, 1978]. On the basis of these data
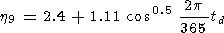 |
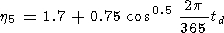 |
The delay time q (in minutes) of intensity variations relative to temperature variations also depends on v and the season:
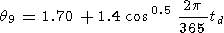 |
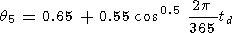 |
The delay times for other vibrational levels have not been sufficiently studied. Assuming a linear dependence on v we have:
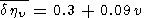 |
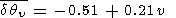 |
While developing the above presented empirical global model of temporal and spatial variations of the OH emissions, attention was primarily paid to obtaining the mean variations and their numerical characteristics. Maximum possible reduction of the measured parameters to the indicated standard solar and geophysical parameters has been made. Only in this case are theoretical calculations corresponding to particular situations possible. The presented set of variations is a first attempt of this kind, and it will doubtless be specified on the basis of specially aimed measurements. All this will influence in a significant way the creation of models of the minor atmospheric constituents, which participate in the photochemical processes of hydroxyl emission generation and whose content can not be practically determined by any other method.
Abalakin, V. K. (Ed.), Astronomical Calendar: Constant Part, 704 pp., Nauka, Moscow, 1981.
Agashe, V. V., et al., Study of mesopause temperature and its behavior from OH nightglow, Indian J. Radio Space Phys., 18 (4), 309, 1989.
Baker, D. J., and A. T. Stair, Rocket measurements of the altitude distributions of the hydroxyl airglow, Phys. Sc., 37 (4), 611, 1988.
Bronshten, V. A., and N. I. Grishin, Noctilucent Clouds, 360 pp., Nauka, Moscow, 1970.
Chapman, S., and R. Lindzen, Atmospheric Tides, 296 pp., D Reidel, Dordrecht, 1972.
Dodd, J. A., et al., OH (v, N) column densities from high-resolution Earth limb spectra, Geophys. Res. Lett., 20 (4), 305, 1993.
Dodd, J. A., et al., Analysis of hydroxyl earthlimb airglow emissions: kinetic model for state-to-state dynamics of OH (v, N), J. Geophys. Res., 99 (D2), 3559, 1994.
Fedorov, V. V., V. N. Glazkov, I. V. Bugaeva, and D. A. Tarasenko, On a relation between the quasi-biennial oscillation of the equatorial stratospheric circulation and variations of atmospheric parameters, Meteorol. Gidrol., 10, 24, 1994.
Fishkova, L. M., Variations of the intensity of the airglow in the near infrared range, Bull. Abastuman. Astrofiz. Obs., 15, 3, 1955.
Fishkova, L. M., On variations of the intensity of the night airglow during stratospheric warmings, Geomagn. Aeron., 18 (3), 549, 1978.
Fishkova, L. M., On variations of population of the vibrational levels of the OH molecules in the upper atmosphere, Polyarn. Siyaniya Svechenie Nochnogo Neba, 29, 9, 1981.
Fishkova, L. M., The Nighttime Airglow of the Midlatitude Upper Atmosphere of the Earth, 272 pp., Metsniereba, Tbilisi, 1983.
Gadsden, M., A secular change in noctilucent cloud occurrence, J. Atmos. Terr. Phys., 52 (4), 247, 1990.
Hernandez, G., et al., Optical determination of the vertical wavelength of propagating 12 hour period upper atmosphere oscillations, Geophys. Res. Lett., 22 (17), 2389, 1995.
Krassovsky, V. I., N. N. Shefov, and V. I. Yarin, Atlas of the airglow spectrum l = 3000-12,400 Å, Planet. Space Sci., 9 (12), 883, 1962.
Krassovsky, V. I., et al., The internal gravity waves near mesopause and hydroxyl emission, Ann. Geophys., 33 (3), 347, 1977.
Kropotkina, E. P., Hydroxyl emission and the meteorology of the stratosphere at Abastumani, Zvenigorod, Loparskaya, and Yakutsk, Polyarn. Siyaniya Svechenie Nochnogo Neba, 24, 37, 1976.
Kropotkina, E. P., and N. N. Shefov, Tidal variations of emissions in the mesopause, Polyarn. Siyaniya Svechenie Nochnogo Neba, 25, 13, 1977.
Kvifte, G. J., Hydroxyl rotational temperatures and intensities in the nightglow, Planet. Space Sci., 15 (10), 1515, 1967.
Lowe, R. P., and L. LeBlanc, Preliminary analysis of WINDII (UARS) hydroxyl data: Apparent peak height, Annual European Meeting on Atmosphere Studies and Optical Methods, Aug. 10-14, 1992, Kiruna, Sweden, Abstracts, p. 94, 1993.
Lowe, R. P., and E. A. Lytle, Balloon-borne spectroscopic observation of the infrared hydroxyl airglow, Appl. Opt., 12 (3), 579, 1973.
Lowe, R. P., K. L. Gilbert, and D. N. Turnbull, High latitude summer observations of the hydroxyl airglow, Planet. Space Sci., 39 (2), 1263, 1991.
Matveeva, O. A., and A. I. Semenov, The results of hydroxyl emission observations during MAP/WINE period: Stratospheric warmings (February, 1984), MAP Newslet., 3, 4, 1985.
Megrelishvili, T. G., and L. M. Fishkova, On variations of the upper atmosphere parameters with the period of about 5.5 years by observations of the twilight and night-time airglow, Geomagn. Aeron., 26 (1), 309, 1986.
Meyes, J., Astronomical Formulae for Calculators, 168 pp., Willman-Bell, Richmond, 1988.
Moreels, G., G. Megie, A. Vallance Jones, and R. L. Gattinger, An oxygen-hydrogen atmospheric models and its application to the OH emission problem, J. Atmos. Terr. Phys., 39 (5), 551, 1977.
Myrab, N. K., C. S. Deehr, and G. G. Sivjee, Large-amplitude nightglow OH(8-3) band intensity and rotational temperature variations during a 24-hour period at 78o N, J. Geophys. Res., 88 (A11), 9255, 1983.
Nelson, D. D., A. Schiffman, and D. J. Nesbit, H + O 3 Fourier-transform infrared emission and laser absorption studies of OH (X2P) radical: An experimental dipole moment function and state-to-state Einstein A coefficients, J. Chem. Phys., 93 (10), 7003, 1990.
Perminov, V. I., and A. I. Semenov, A nonequilibrium of the rotational temperature of the OH bands with high vibrational excitation, Geomagn. Aeron., 32 (2), 175, 1992.
Perminov, V. I., A. I. Semenov, N. N. Shefov, and V. V. Tikhonova, Evaluation of the seasonal variations of the altitude of the hydroxyl emission layer in the upper atmosphere, Geomagn. Aeron., 33 (3), 113, 1993.
Petitdidier, M., and H. Teitelbaum, Lower thermosphere emissions and tides, Planet. Space Sci., 25 (8), 711, 1977.
Potapov, B. P., V. G. Sobolev, V. A. Sukhodoev, and V. N. Yarov, Measurements of the altitude of the hydroxyl emission layer near Moscow, Geomagn. Aeron., 23 (2), 326, 1983.
Rapoport, Z. Ts., On a possible reason of winter disturbances in the ionospheric D region, Dok. Akad. Nauk SSSR, 271 (5), 1103, 1983.
Reid, G. C., Seasonal and interannual temperature variations in the tropical stratosphere, J. Geophys. Res., 99 (D9), 18,923, 1994.
Reshetov, V. D., Variability of the Meteorological Parameters in the Atmosphere, 216 pp., Gidrometeoizdat, Leningrad, 1973.
Scheer, J., and E. R. Reisen, Rotational temperatures for OH and O 2 airglow bands measured simultaneously from El Leonicito (31o 48 ' S), J. Atmos. Terr. Phys., 52 (1), 47, 1990.
Semenov, A. I., and L. M. Fishkova, Climatic trends in the upper atmospheric temperature and composition according to nightglow data during last four decades, paper presented at IUGG Meeting S201, Int. Union of Geod. and Geophys., Boulder, 1995.
Semenov, A. I., and N. N. Shefov, Comparison of atmospheric temperatures according to CIRA 72 and nightglow data, Space Res., 19, 203, 1979.
Semenov, A. I., and N. N. Shefov, Impact of the internal gravity waves on the dynamics and energetics of the upper atmosphere (from parameters of its emissions), Ionos. Issled., 47, 24, 1989.
Shagaev, M. V., Parameters of the hydroxyl emission variations, which manifest the processes of its generation, Polyarn. Siyaniya Svechenie Nochnogo Neba, 27, 18, 1978.
Shefov, N. N., On determination of the vibrational temperature of the OH bands, Polyarn. Siyaniya Svechenie Nochnogo Neba, 5, 5, 1961.
Shefov, N. N., Some properties of the hydroxyl emission, Polyarn. Siyaniya Svechenie Nochnogo Neba, 13, 37, 1967.
Shefov, N. N., Behavior of the upper atmosphere emissions during high meteoric activity, Planet. Space Sci., 16 (1), 134, 1968.
Shefov, N. N., Hydroxyl emission of the upper atmosphere, I, Behavior during solar cycle, seasons and geomagnetic disturbances, Planet. Space Sci., 17 (5), 797, 1969.
Shefov, N. N., Hydroxyl emission of the upper atmosphere, III, Diurnal variations, Planet. Space Sci., 19 (2), 129, 1971.
Shefov, N. N., Hydroxyl emission, Ann. Geophys., 28 (1), 137, 1972.
Shefov, N. N., Relations between the hydroxyl emission of the upper atmosphere and the stratospheric warmings, Gerlands Beitr. Geophys., 82 (2), 111, 1973.
Shefov, N. N., Lunar tidal variations of hydroxyl emission, Indian J. Radio Space Phys., 3 (3), 314, 1974a.
Shefov, N. N., Lunar variations of the hydroxyl emission, Geomagn. Aeron., 14 (5), 920, 1974b.
Shefov, N. N., The results of hydroxyl emission studies, Polyarn. Siyaniya Svechenie Nochnogo Neba, 22, 71, 1975.
Shefov, N. N., Seasonal variations of the hydroxyl emission, Polyarn. Siyaniya Svechenie Nochnogo Neba, 24, 32, 1976.
Shefov, N. N., The height of the hydroxyl emission layer, Polyarn. Siyaniya Svechenie Nochnogo Neba, 27, 45, 1978a.
Shefov, N. N., A non-corpuscular origin of the ionospheric absorption occurring at middle latitudes after geomagnetic storms, Polyarn. Siyaniya Svechenie Nochnogo Neba, 27, 36, 1978b.
Shefov, N. N., and N. A. Piterskaya, Spectral, spatial, and temporal characteristics of the background airglow. The hydroxyl emission, Polyarn. Siyaniya Svechenie Nochnogo Neba, 31, 23, 1984.
Shefov, N. N., and T. I. Toroshelidze, Upper atmosphere emissions as an indicator of the dynamical processes, Polyarn. Siyaniya Svechenie Nochnogo Neba, 23, 42, 1975.
Shefov, N. N., and V. I. Yarin, Latitudinal and planetary variations of the hydroxyl emission, Polyarn. Siyaniya Svechenie Nochnogo Neba, 9, 19, 1962.
Sukhodoev, V. A., et al., The orographic effect in the upper atmosphere, Izv. Akad. Nauk SSSR, Fiz. Atmos. Okeana, 25 (9), 926, 1989.
Takahashi, H., Y. Sahai, and P. P. Batista, Tidal and solar cycle effects on the O1 5577 Å, Na D and OH(8-3) airglow emissions observed at 23o S, Planet. Space Sci., 32 (7), 897, 1984.
Takahashi, H., Y. Sahai, and N. R. Teixeira, Airglow intensity and temperature response to atmospheric wave propagation in the mesopause region, Adv. Space Res., 10 (10), 77, 1990.
Taranova, O. G., and T. I. Toroshelidze, On OH emission measurements at twilights, Polyarn. Siyaniya Svechenie Nochnogo Neba, 18, 26, 1970.
Thomas, G. E., et al., Relation between increasing methane and the presence of ice clouds at the mesopause, Nature, 338, 490, 1989.
Toroshelidze, T. I., Results of spectrographic observations of the hydroxyl emission in the 10,600-11,200 Å in twilights, Soobshch. Akad. Nauk Gruz. SSR, 52 (1), 57, 1968.
Toroshelidze, T. I., Variations of the rotational temperature of the hydroxyl emission, Polyarn. Siyaniya Svechenie Nochnogo Neba, 23, 33, 1975.
Toroshelidze, T. I., Analysis of the Aeronomical Problems From the Upper Atmosphere Emissions, 217 pp., Metsniereba, Tbilisi, 1991.
Turnbull, D. N., and R. P. Lowe, Vibrational population distribution in the hydroxyl night airglow, Can. J. Phys., 61 (2), 244, 1983.
Turnbull, D. N., and R. P. Lowe, New hydroxyl transition probabilities and their importance in airglow studies, Planet. Space Sci., 37 (6), 723, 1989.
Turnbull, D. N., and R. P. Lowe, Temporal variations in the hydroxyl nightglow observed during ALOHA 90, Geophys. Res. Lett., 18 (7), 1345, 1991.
Wiens, R. H., and G. Weill, Diurnal, annual and solar cycle variations of hydroxyl and sodium nightglow intensities in the Europe-Africa sector, Planet. Space Sci., 21 (6), 1011, 1973.
Yarin, V. I., Relation of the hydroxyl emission to the meteorological conditions at Yakutsk, Polyarn. Siyaniya Svechenie Nochnogo Neba, 18, 18, 1970.