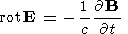
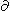 Bz0/
Bz0/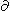 t,
where r is the
cylindrical distance, El
is the eastern component of the electric field, and Bz0
is the magnetic disturbance at the Earth.
t,
where r is the
cylindrical distance, El
is the eastern component of the electric field, and Bz0
is the magnetic disturbance at the Earth.
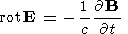
| (1) |
Estimates performed by a number of authors show that the induction fields are often commensurate with the fields of quasi-stationary magnetospheric convection.
Mal'tsev et al. [1975] determined the field associated with a change in the system of field-aligned currents. At first the magnetic field was calculated, and then the electric field was found from (1) and from the condition of high electric conductivity

| (2) |
From analysis of the experimental data, Sergeev [1984] showed that the induction field in the plasma sheet during the initial phase of a substorm is close in magnitude and opposite in sign to the electrostatic field, and as a result the total field in the plasma sheet turns out to be at least an order of magnitude weaker than the field in the tail lobes.
Pudovkin et al. [1991] studied the induction field resulting from a change in the plasma sheet geometry during the expansion of the substorm. It was shown that the magnitude of the induction field at the reconnection point is proportional to the velocity of motion of the auroral bulge toward the pole (under the condition that the reconnection point does not displace).
Kozlovsky et al. [1994] considered the consequences of enhancement of the solar wind dynamic pressure. The image magnetospheric model was used. The pressure enhancement was imitated by motion of an imaginary dipole toward the Earth. It was assumed that the electric field in the magnetosphere can be obtained through Lorentz transformations
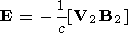
| (3) |
The goal of this paper is to calculate the induction electric field in the magnetosphere during sudden increases of solar wind dynamic pressure (sudden impulse (SI) or storm sudden commencement (SSC)).
We use the image dipole, vacuum model of the magnetosphere
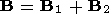
| (4) |

| (5) |
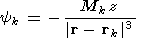
| (6) |
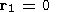
| (7) |

| (8) |
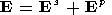
| (9) |
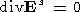
| (10) |
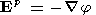
| (11) |
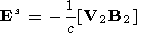
| (12) |
By substituting (9), (11), and (12) into formula (2), we obtain the equation for the potential
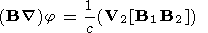
| (13) |
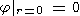
| (14) |
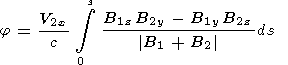
| (15) |
We restrict ourselves to calculating the integral in (15) in the first approximation when inequalities
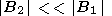
| (16) |

| (17) |
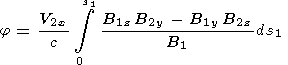
| (18) |
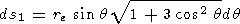
| (19) |
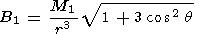
| (20) |
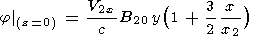
| (21) |
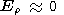
| (22) |
The field El can be written in a different manner. By differentiating (5) with respect to time at the point r = 0 and taking into account (6) and (8), we obtain
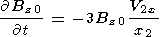
| (23) |

| (24) |
In contrast to the electrostatic field, the induction field is not transmitted to the ionosphere. The condition of freezing-in (2) is not violated in this case. The magnetic field lines remain as if fixed at the level of the ionosphere and experience maximum displacements in the equatorial plane of the magnetosphere.
As compression of the magnetosphere by the solar wind increases, the induction electric field, according to (24), is westward directed and causes the plasma drift toward the Earth both in daytime and at night. This is the difference between our result and the conclusions of Kozlovsky et al. [1994], who state that the induction field is directed from evening to morning and forces the plasma to move from the Sun in all longitudinal sectors. We have noted above that Kozlovsky et al. [1994] use a wrong expression for the induction field (3) contradicting the condition of freezing-in (2).
The trapped particles are energized during compression of the magnetosphere by the solar wind. This occurs because of the betatron acceleration. The induction electric field enhances this effect by several fold because in the reference system associated with the displacing magnetic field tube the magnetic field is enhanced to a larger degree than in the magnetosphere as a whole. Variations in the magnetic field in the tube can be written as
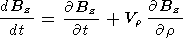
| (25) |
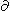 Bz/
Bz/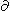 t
is the local (Euler) derivative; and
Vr =
cEl/Bz
is the velocity of radial drift in the induction
electric field. Under condition (16), we obtain from (4)-(6)
t
is the local (Euler) derivative; and
Vr =
cEl/Bz
is the velocity of radial drift in the induction
electric field. Under condition (16), we obtain from (4)-(6)
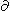 Bz/
Bz/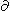 r =
-3Bz/r. In view of (24),
we infer from (25)
r =
-3Bz/r. In view of (24),
we infer from (25)
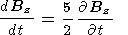
| (26) |
Knott et al. [1985] and Laakso and Schmidt [1989] reported the electric field measurements by the geosynchronous satellite r = 6.6RE immediately after a SSC. Knott et al. [1985] studied two SSC events during each of which the electric amplitude burst reached ~5 mV m-1. During the first event, the magnetic field increased by 12 nT. These magnitudes are consistent with (24). As far as the electric field direction is concerned, it contained a radial (from the Earth) component somewhat exceeding the azimuthal one, in addition to the westward component. The measurement was performed at the pre--noon sector (~1100 LT). In the second case, the measurement was carried out almost at noon, and the electric field proved to be directed eastward, which agrees with formula (24) because the magnetic field impulse was negative. The magnitude of the magnetic impulse of the second event was not given by Knott et al. [1985].
Laakso and Schmidt [1989] investigated 27 cases of SSC. Figure 3 of
Laakso and Schmidt [1989] showed vectors E for the moments when
DBz reached 50% of the maximum value.
On average, there was a
westward directed azimuthal component of the order of 1 mV m-1.
The average values of 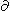 Bz/
Bz/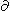 t
were not given. It follows from (24)
that they should be
t
were not given. It follows from (24)
that they should be 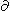 Bz0/
Bz0/ 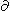 t
~0.025 nT s-1.
t
~0.025 nT s-1.
In addition to the azimuthal component of the electric field, Figure 3 of Laakso and Schmidt [1989] shows a radial component of 1-2 mV m-1. In the morning sector it is directed away from the Earth, and in the evening sector it is directed toward the Earth. Probably the appearance of the radial component is caused by the polarization currents at the front of the magnetoacoustic wave propagating from the daytime magnetopause to the magnetospheric tail. Propagation of such a wave with the velocity of ~1000 km s-1 was detected by several satellites [Nopper et al., 1982] for one SI event.
An incompletely understood consequence of SI and SSC is the train of Alfvén oscillations in the range of periods of Pc 4-5 with the amplitude (in the magnetosphere) commensurate with the intensity of the primary magnetoacoustic impulse [Knott et al., 1985; Laakso and Schmidt, 1989; Nopper et al., 1982; Tverskaya and Khorosheva, 1982]. In a uniform medium, the Alfvén and magnetoacoustic waves propagate independently. Different mechanisms for transformation of the magnetoacoustic wave into an Alfvén wave have been suggested, such as changes in the ionospheric conductivity [Safargaleev and Mal'tsev, 1987] or irregularities of the magnetospheric plasma [Kozlovsky et al., 1994; Lysak and Lee, 1992].
SIs and SSCs are also accompanied by enhancement of particle injections. On the whole, the injected flux in the auroral region can be enhanced by 2-3 fold [Craven et al., 1986].
Measurements of fluxes of trapped particles by several geosynchronous satellites during one of the SSC events showed that energization of particles agrees with the theory of betatron acceleration to an order of magnitude [Wilken et al., 1986], though it should be taken into account that the plasma motion toward the Earth during an SSC leads to additional temporal variations in the fluxes because of the presence of a radial gradient in the particle pressure. In addition to acceleration, a change in the pitch angle distribution was observed; it acquired the shape of a "butterfly." Wilken et al. [1986] suppose that this is caused by splitting of the drift shells for particles with different pitch angles. Note that splitting is accompanied by separation of electrical charges, which can give a certain contribution to generation of the Alfvén wave observed after SI or SSC.
Craven, J. D., et al., Global auroral responses to magnetospheric compressions by shocks in solar wind: Two case studies, in Solar Wind-Magnetosphere Coupling, edited by Y. Kamide and J. A. Slavin, pp. 367-380, TERRAPUB, Tokyo, 1986.
Knott, K., A. Pedersen, and U. Wedeken, GEOS 2 electric field observations during a sudden commencement and subsequent substorms, J. Geophys. Res., 90, (A2), 1283-1288, 1985.
Kozlovsky, A. E., V. V. Safargaleev, and W. B. Lyatskiy, The transformation of magnetoacoustic waves into Alfvén waves inside the magnetosphere, Ann. Geophys., 12 (10/11), 1022-1026, 1994.
Laakso, H., and R. Schmidt, Pc 4-5 pulsations in the electric field at geostationary orbit (GEOS 2) triggered by sudden storm commencements, J. Geophys. Res., 94 (A6), 6626-6632, 1989.
Lysak, R. L., and D.-H. Lee, Response of the dipole magnetosphere to pressure pulses, Geophys. Res. Lett., 19 (9), 937-940, 1992.
Mal'tsev, Yu. P., S. V. Leont'ev, and S. V. Lyatskiy, Induction electric fields during a substorm, Geomagn. Aeron., 15 (3), 519-523, 1975.
Nopper, R. W., Jr., W. J. Hughes, C. G. MacLennan, and R. L. McPherron, Impulse-excited pulsations during the July 29, 1977, event, J. Geophys. Res., 87 (A8), 5911-5916, 1982.
Pudovkin, M. I., V. S. Semyenov, G. V. Starkov, and T. A. Kornilova, On separation of the potential and vortex parts of the magnetotail electric fields, Planet. Space Sci., 39 (4), 563-568, 1991.
Safargaleev, V. V., and Yu. P. Mal'tsev, Generation of the preliminary impulse and long-period pulsations during SI, Geomagn. Aeron., 27 (2), 247-252, 1987.
Sergeev, V. A., Regularities in development of intense isolated substorms from observations in the plasma sheet of the magnetosphere, Magnitosfer. Issled., 5, 71-82, 1984.
Tverskaya, L. V., and O. V. Khorosheva, On the nature of the source of packets of decaying long-period pulsations, Geomagn. Aeron., 22 (5), 824-830, 1982.
Wilken, B., et al., Magnetospheric configuration and energetic particle effects associated with a SSC: A case study of the CDAW 6 event on March 22, 1979, J. Geophys. Res., 91 (A2), 1459-1473, 1986.