In this paper we continue the investigation of tidal impact on the diurnal, vertical, and frequency variations of parameters of the midlatitude Es layer using data from closely located radar and ionospheric stations.
The database of velocity components of the neutral wind in the meteor zone resulted from measurements made by the meteor radar in Obninsk (55oN, 38oE).
The distance between the regions observed by the ionosonde and the radar is about 500 km and is less than the spatial scale of pulsations of the parameters of the semidiurnal tide (~1500 km [Portnyagin, 1981]).
Long-duration observations of the winds in the meteor zone show that the semidiurnal harmonic provides the principal contribution to the mid- and high latitude tidal motions [Lysenko et al., 1994]. According to classic tidal theory the semidiurnal tide is a superposition of various modes [Chapman and Lindzen, 1972; Hines, 1995], the main contribution to the semidiurnal tide at middle latitudes being provided by the (2, 2), (2, 4) and (2, 6) modes [ Fakhrutdinova and Ishmuratov, 1991]. In the northern hemisphere, the spatial hodograph of the wind velocity of any mode is a left-handed corkscrew [ Akchurin et al., 1995]. Thus the nodes in the tidal mode for one oscillation period are situated along the vertical in the following order (up from below): DM, CZ, CM, and DZ (any cyclic permutation of the nodes is possible if the mode is a propagating wave). Each tidal mode has its own value of downward phase velocity (the velocity of any node of the mode), in particular: ~12.5 km h-1, ~4.0 km h-1, and ~2.5 km h-1 for the (2, 2), (2, 4), and (2, 6) modes, respectively. When it is necessary in the following arguments to emphasize that the chosen node belongs to a particular mode of the semidiurnal tide, the mode number in parentheses will be added to the name of the node. For example, DZ(2) and DZ(6) denote the diverging nodes of the (2, 2) and (2, 6) zonal modes, respectively.
If there is only one tidal mode, WST predicts that the Es layers should be formed and descend in the converging nodes of this mode. Initially, the Es layer would move together with the CM node down to 120-130 km altitude, and then it would move together with the CZ node down to 90-100 km altitude. At altitudes of about 120 km (where the meridional convergence is changed by the zonal one) an accelerated motion of the Es layer from the CM node to the CZ node with a velocity which exceeds the phase velocity of the given mode, should be observed [Chimonas, 1973].
Let us call the Es descents with velocities which exceed the phase velocity of the (2, 2) mode, "superfast" descents; the descents with equal velocities the "fast" descents, and the descents with lower velocities the "slow" descents.
The descent of the Es layer will occur down to a definite altitude, below which the converging CZ node would not be able to entrain this layer because of the increase in the collision frequency of the ions. This is called the damping altitude and depends on the phase velocity of the tidal mode and the atomic mass of the transported ions [ Chimonas and Axford, 1968].
For tidal modes with phase velocities above 3.6 km h-1 the damping height is about 100 km, and for modes with lower velocities the damping height is 90-95 km [ Mathews and Bekeny, 1979]. Actually there exist in the atmosphere not only various tidal modes, but also gravity waves of nontidal origin. Thus the behavior of the Es layers could well be different from that described above.
Data from the Obninsk meteor radar (which does not measure echo altitude) provide the mean wind velocity over the meteor zone at an average altitude of 95 km [ Lysenko et al., 1994]. A determination of the vertical position of the node points is possible only by using the above theoretical representation of the semidiurnal tide.
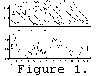An example of typical diurnal variations of the real height and
frequency parameters of the Es layers is presented
in Figure 1 as
observed on July 3, 1993 (the afternoon), and July 4, 1993 (the
entire day). To reveal the possible influence of various modes of
the semidiurnal tide on variations in the Es layer
altitude, Figure 1
shows the trajectories of descent of various nodes of the (2, 2)
(dashed lines) and (2, 6) (dashed-dotted lines) modes. These
trajectories are drawn in such a way that they intersect the 95-km
altitude when the corresponding node (the name of the node is shown
in the upper part of the trajectory) was measured by the meteor
radar. To simplify the figure, the descent of the nodes of the (2, 6)
mode is represented only by the descents of the CZ node,
and the
descents of the nodes of the (2, 4) mode are not shown at all. Most
of the time the Es layers of the "main" type
(thin line in Figure 1a)
descend with a velocity close to the phase velocity of the (2, 6)
mode. However, the Es layers of the
"accompanying" type (the
thick line) often shift downward with a velocity either equal to or
exceeding the phase velocity of the (2, 2) mode. Part of these
"fast" or "superfast" descents of the "accompanying" Es
(marked by
the double line under the horizontal axis in Figure 1a) occur at
approximately the same altitudes and at the same time as the
descents of the DM(2) node (at 0500-0600 LT in the
morning and at
1800-1900 LT in the evening). This fast downward motion of the
Es layer cannot be accounted for by a transition
of the layer from the
CM(2) node to the CZ(2) node - the radar
measurements of nodal
times do not match. Nor can the motion be explained by the action of
the DM(2) node as described by the WST approximation.
The DM node is
divergent, so formation and motion of the Es layer
with this node
are impossible. However, the accumulation of positive ions near
(above) the DM node, where the maximum of the
eastward wind is
located, is possible owing to the change with height of the effect
of the Earth's magnetic field on ion motion. For example,
accumulation of the ions at some altitude (above 120 km) under the
action of only the homogeneous eastward wind would occur owing to
the fact that the ions from the lower layers are accelerated to
higher vertical velocity than the ions from the upper layers because
the magnetic field effect increases with altitude. The divergence of
the positive ion concentration above the DM(2) node is
weakened by
the two processes described above, in which two components of the
zonal thermospheric wind participate: the prevailing wind (via the
vertical gradient of the magnetic field effect) and the semidiurnal
component (via the vertical gradient of the zonal wind velocity
favorable for ion compression). The efficiency of these processes,
which compensate for ion divergence, grows as the
DM(2) node
approaches the altitude of 120 km. So the point of total
compensation of the divergence would move down with a velocity
exceeding the phase velocity of the tide. The trajectory of the
motion of the layers formed at this point would be steeper than the
trajectory of the DM node (see 0500-0600 LT on
July 4 in Figure 1).
The competition between the actions of the meridional and zonal
components of the thermospheric wind leads to the formation of low
intensity layers. Figure 1 demonstrates that the
Es layers formed
by the action of the DM node (at 0500-0600 LT or
1800-1900 LT) are
located above or near this node (Figure 1) and have small critical
frequency values (in Figure 1 they exceed
foE by only 0.2-0.5 MHz).The trajectories of other "fast" descents of the Es layers are due to the CZ(2) nodes in the 100-120 km interval (shown by the single line below the horizontal axis in Figure 1). Such descents occur at 1000-1200 LT and 2100-2400 LT (except for the "superfast" descent of the "accompanying" layer at 2100-2200 LT on July 3). Figure 1 shows that the Es layers are able to move either under the action of only the CZ(2) node or under the action of two nodes (CZ(2) and CZ(6)) with later merging of the Es layers, which existed at these nodes. The damping altitude for the (2, 2) mode is higher than that for the (2, 6) one; so the Es layer formed after the merging of the CZ(2) and CZ(6) nodes moves further with the CZ(6) node.
The limiting frequencies of the "main" and "accompanying" Es layers exceed the foE values by about 2-3 times when the CZ(2) node passes the 100-120 km height interval (Figure 1). When the CZ(2) node descends to 95 km (these times are indicated in Figure 1 by the vertical dashed lines), the values of the limiting frequencies rapidly decrease and become equal to foE.
The trajectories of the descents of the CZ(6) nodes (shown by dashed-dotted lines) in Figure 1 are theoretical, because the absence of an altimeter at the Obninsk meteor radar installation does not allow reliable determination of the phase of this mode. This fact may explain the small discrepancy in time (about 2 hours) between the trajectories of the "slow" descents of the CZ(6) node and the Es layer (Figure 1).
Thus the short interval between the vertical sounding sessions (15 min) and detailed analysis of the ionograms has made it possible to reveal the action of the (2, 2) mode on the Es layer motions, which has not been done in previous analyses of the hourly data of the stations of the ionospheric network [ Fomichev and Shved, 1981; Gorbunova and Shved, 1984]. This tidal mode is often observed in summer in measurements of the wind in the meteor zone [ Lysenko et al., 1994].
Unfortunately, the processes in the lower thermosphere are significantly influenced not only by the wind shears, but also by various photochemical processes, particle precipitation, intensification of the external electric field, nonlinear interaction of the internal gravity waves (IGW), etc. That is why a clear relationship between variations of the ionospheric and wind parameters as described above is not observed continuously. To study this relationship a statistical analysis of the monthly set of data on frequency and height parameters of the Es layer has been carried out.
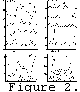The hourly mean values of the vEs velocity of descent
of the
Es layers and the probability of their
appearance P(vEs) for the
velocity intervals >15 km h-1,
10-15 km h-1, 4-10 km h-1,
and 0-4 km h-1
were calculated to provide a more accurate determination of the
influence of the modal composition of the semidiurnal tide on
Es layer motions. The results of the calculations
for the "main" and
the "accompanying" Es layers are presented in
Figures 2a and 2b,
respectively. The limits of the above intervals were chosen in such
a way that curve 1 (v > 15 km h-1)
characterizes the probability of
the Es layer descending with a velocity which
exceeds the phase
velocity of the (2, 2) mode, and curves 2, 3, and 4
(v < 15 km h-1)
characterize descents with velocity close to the phase velocities of
the (2, 2), (2, 4), and (2, 6) modes, respectively.
Diurnal variations of the frequency parameters of the Es layers were studied on the basis of the parameter dfoEs = foEs - foE, where foE is the critical frequency of the E layer. This parameter makes it possible to exclude the influence of the background ionization in the diurnal variations of foEs. Figures 2c and 2d show the probability of appearance P(dfoEs) for dfoEs exceeding the values 5 MHz, 3 MHz, 1 MHz, 0.3 MHz, and 0.1 MHz for the "main" and "accompanying" layers, respectively.
Let us consider the diurnal variations of the frequency and height parameters of the "main" Es layer. Analysis of the set of P(vEs) curves (see Figure 2a) shows that the most probable descent velocity of the Es layers is at a velocity close to the phase velocity of the (2, 6) mode. The probability of motion with this velocity (curve 4) is equal to about 45%, a value that exceeds by 2-3 times the probability of downward motion with velocities close to the phase velocities of the (2, 2) and (2, 4) modes. Therefore the "main" Es layer is apparently located in the CZ(6) converging node.
However, the diurnal variations of the frequency parameters indicate a significant influence of the DZ(2) and CZ(2) nodes of the zonal wind. For example, at 0900-1100 LT and 2100-2300 LT in the periods of CZ(2) node passage of the region of zonal convergence (marked by the single line under the horizontal axis in Figure 2c), an increase of the Es layer intensity occurs. Times of minima in the curves of the P(dfoEs) family at 0600 LT and 1800 LT (the double line under the horizontal axis in Figure 2c) can be related to a passage of the 95-100 km interval by the DZ(2) node. Disappearance of the Es layers from the 95-110 km interval due to this node makes it possible to observe in the ionograms descents of the "accompanying" Es layers due to action of the wind system near the DM(2) node (such events are marked by the double line under Figure 1a).
As was mentioned previously, the "accompanying" Es layer consists of Es layers of several types (for example, consequent and additional). That is why the set of the P(vEs) curves for the "accompanying" Es layer (Figure 2b) demonstrates more complicated diurnal variations than that of the "main" Es layer. Using the results of the analysis of the diurnal variations presented above, one can state that the maximum of curve 1 (superfast descent) at 0600 LT is due to the action of the diverging DM (the double line under the horizontal axis in Figure 2d). The evening (superfast) descent of this node at 1800 LT is not manifested in curve 1 as in the morning because it is screened by the Es layers located below during the beginning of the descent. A typical value of dfoEs for the "accompanying" Es layer formed by the DM(2) node is 0.3-0.5 MHz. The probability of appearance of layers with such values of dfoEs is characterized by the distance between curves 4 and 5 (Figure 2d). The distance maximizes at the same times (0600 LT and 1800-1900 LT).
Though action of the CZ(2) node (marked by the single line under the horizontal axis in Figure 2d) is clearly manifested in variations of curves 1-3 of the P(vEs) family for the "accompanying" Es layer in the evening, in the daytime the action is more weakly manifested in curve 2 (~5%) owing to screening by the layers located below. Analysis of the evening maxima in curves 1-3 (at 2200-2300 in Figure 2b) shows that the probability of superfast descents exceeds the probability of fast ones by a factor of 2. This fact may be explained by superfast transitions of the Es layers between the CM(2) and CZ(2) nodes, which are observed at night owing to the absence of screening by the layers located below. However, action of the CZ(2) node in the diurnal variations of curves of the P(dfoEs) family for the "accompanying" Es is manifested both in the daytime and in the evening (at 0900-1100 LT and 2200-2300 LT in Figure 2d). The other maxima (at 0200 LT and 1500 LT) in the curves of the P(vEs) and P(dfoEs) families for the "accompanying" Es layers ( Figures 2b and 2d) apparently are related to passage of the CM(2) node. The CM(2) node is convergent above 120 km; the Es layers formed in it should be destroyed at altitudes below 115 km. This can be seen in Figure 1a at 0300 LT on July 4 and at 0200 LT on July 5 (the events are marked by the asterisks under the horizontal axis).
Upward motions of the Es layers of all types (not shown in Figure 1) in most cases are apparent. They may be caused by appearance of lateral reflections, or by reflections from the layers above and interruption (weakening) of reflections from the layers situated below or closer. However, as was mentioned by Mathews and Bekeny [1979], the upward motions may also be related to the destruction in some particular altitude range of some tidal mode and transportation of the long-lived ions from its converging node into a node of another mode located above.
Thus analysis of the curves of the P(vEs) and P(dfoEs) families of the "main" and "accompanying" Es layers confirms the conclusions regarding the influence of the (2, 2) mode nodes on Es layer formation, which have been made earlier on the basis of consideration of the diurnal variations of the real height and critical frequency of the Es layer for particular days.
In addition to the above mechanisms, the following processes may influence formation and motion of Es layers: a sharp intensification of the external electric field [ Gershman et al., 1976], which is equivalent to an increase of the wind velocity in a converging node; interaction (nonlinear) of several IGW, which leads to a convergence of ions not only in the vertical direction, but in the horizontal direction as well [ Gershman et al., 1976]; and precipitation of energetic particles [ Chavdarov et al., 1975].
Many observed properties of the summer diurnal variations of the parameters of the midlatitude Es layer are explained by action of the (2, 2) semidiurnal mode, in particular: appearance at 0600 LT and 1900 LT of "extra fast" descents of the consequent Es layers in the 120-160 km height interval is due to action of the wind system near the DM node; appearance at 0900-1100 LT and 2100-2300 LT of "fast" descents of either the "main" Es layer (if the "accompanying" one is absent) or the "accompanying" one with consequent merging with the "main" layer at altitudes of 100-120 km is due to action of the CZ node; the values of foEs for these Es layers are high at 0000 LT and 0900-1200 LT, when the CZ node passes the 100-115 km altitude interval, and decreases to foE, when the CZ node descends to an altitude of 95 km.
Chapman, S., and R. S. Lindzen, Atmospheric Tides, D. Reidel, Dordrecht, 1970.
Chavdarov, S. S., Yu. K. Chasovitin, S. P. Chernysheva, and V. M. Sheftel, The Midlatitude Sporadic Layer of the Ionospheric E Region, 120 pp., Nauka, Moscow, 1975.
Chimonas, G., Wind component exchange and the rapid vertical movement of a sporadic E layer, J. Geophys. Res., 78 (25), 5636, 1973.
Chimonas, G., and W. I. Axford, Vertical movement of temperate-zone sporadic E layers, J. Geophys. Res., 73 (1), 111, 1968.
Fakhrutdinova, A. N., and R. A. Ishmuratov, Seasonal variations of the contribution of modes in the semidiurnal tidal motions in the midlatitude lower thermosphere, Geomagn. Aeron., 31 (5), 904, 1991.
Fomichev, V. I., and G. M. Shved, On the height and probability of formation of the Es layer at moderate latitudes, Geomagn. Aeron., 21 (4), 630, 1981.
Gershman, B. N., Yu. A. Ignat'ev, and G. Kh. Kamenetskaya, Mechanisms of Formation of the Ionospheric Sporadic E Layer at Various Latitudes, 108 pp., Nauka, Moscow, 1976.
Gorbunova, T. A., and G. M. Shved, Analysis of the semitransparence of the Es layer as an indicator of the turbulence under dynamically homogeneous conditions, Geomagn. Aeron., 24 (1), 30, 1984.
Hines, C. O., Atmospheric gravity waves, in Thermospheric Circulation, p. 85, Mir, Moscow, 1975.
Lysenko, I. A., et al., Wind regime at 80-110 km at mid-latitudes of the northern hemisphere, J. Atmos. Terr. Phys., 56 (1), 31, 1994.
Mal'tseva, O. A., S. P. Chernysheva, and V. M. Sheftel, Comparison of the real and virtual height of the Es sporadic layer, Geomagn. Aeron., 13 (2), 361, 1973.
Mathews, J. D., and F. S. Bekeny, Upper atmosphere tides and the vertical motion of ionospheric sporadic layers at Arecibo, J. Geophys. Res., 84\,(A6), 2743, 1979.
Minullin, R. G., et al., A Digital Ionospheric Facility "Tsyklon-9", Kazan' University Press, Kazan', Russia, 1994.
Portnyagin, Yu. I., Large-scale irregularities in the wind field at altitudes of 80-100 km, Izv. Acad. Sci. USSR Atmos. Okeanic Phys., 17 (3), 236, 1981.
Robinson, B. J., On some disturbances in the E region, J. Atmos. Terr. Phys., 19, 160, 1960.
Whitehead, J. D., Recent work on mid-latitude and equatorial sporadic Es, J. Atmos. Terr. Phys., 51 (5), 401, 1989.