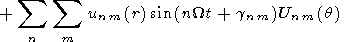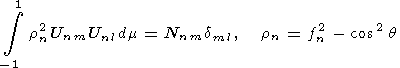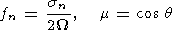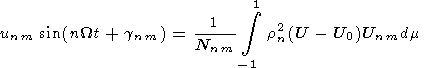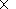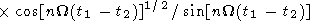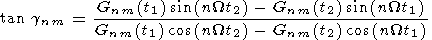International Journal of Geomagnetism and Aeronomy
Published by the American Geophysical Union
Vol. 1, No. 1, April 1998
The method of calculation of the tide variations in the lower
thermosphere from the UARS wind measurements
I. V. Karpov
Institute of Terrestrial Magnetism, Ionosphere, and Radio
Wave Propagation, Troitsk, Moscow Region, Russia
Contents
Abstract
From measurements of the wind horizontal
components by the Upper Atmosphere Research satellite (UARS) in February 1992 the
amplitudes and phases of the Hough functions for the diurnal and
semidiurnal solar migrating tides are calculated. The calculations
demonstrate that the structure of the semidiurnal tide in the lower
thermosphere is mainly determined by the ( 2,2) and (2,4) tidal
modes. At altitudes of 90-100 km the (2,3) mode contribute
significantly to the tidal structure. The (1,-1) and (1,-2) evanescent modes of the
diurnal tide are responsible for a considerable portion of the tidal structure below 90 km. The calculated amplitudes of the
tidal modes exceed the amplitudes of the corresponding modes measured by
radars. The phases of the tidal modes determined for the
zonal wind component as measured by the satellite agree with the
results of radar observations. The amplitudes and phases of the
diurnal and semidiurnal tides at middle latitudes are calculated
using the mode structure determined from the satellite measurements.
The calculated tidal amplitudes exceed the amplitudes obtained in
radar observations. Good agreement with radar observations is
obtained for the times of maximuma in both the diurnal and
semidiurnal tides in the zonal component of the wind velocity.
Introduction
Tides in the upper atmosphere are determined as global wave perturbations of
the hydrodynamic parameters with periods rigorously equal to 24 h/n ( n is integer) are meant. The longitudinal and latitudinal
variations of the tides are described by the zonal harmonics and
tidal modes: the Hough functions which are solutions of the tidal
Laplace equation. This definition makes it possible to consider the
observed variations of atmospheric parameters with the periods,
which correspond to the tidal disturbances, as a superposition of
the tidal modes. Therefore, the problem of determination of tidal
parameter variations in the atmosphere is reduced to determination
of the amplitudes and phases of the Hough functions.
Radar observations of the horizontal wind components are usually
used to determine the mode composition of the tides in the lower
thermosphere and mesosphere. The methods used to calculate the
amplitudes and phases of the Hough functions are based on analysis
of the vertical structure of the observed parameters
[ Fakhrutdinova and Ishmuratov, 1991;
Forbes and Salah, 1991].
However, due to
difficulties of providing continuous observations and to
inhomogeneous distribution of the ground-based stations, the
parameters of the tidal variations in the lower thermosphere are
not adequately studied and need specification.
The use of satellite observations, for example the winds measured
by UARS satellite, provides a significant expansion of the
experimental data on the tides in this atmospheric region. To
measure winds in the mesosphere and lower thermosphere, the HRDI
instrumentation (High Resolution Doppler Imager) is installed on
board the satellite and makes it possible to provide measurements
at altitudes of  50-115 km in the daytime and
50-115 km in the daytime and 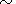 90 km at
night. The detailed description of the HRDI and of its functioning
on board UARS was given by
Hays et al. [1993].
The orbit parameters
provide measurements in the
90 km at
night. The detailed description of the HRDI and of its functioning
on board UARS was given by
Hays et al. [1993].
The orbit parameters
provide measurements in the 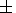 72o latitude band. During 24
hours the measurements cover all the longitudes. The results of
observations of the wind tidal variations by the HDRI were
presented by
Burrage et al. [1995a, b\link2]
and
Hays et al. [1993, 1994].
It is worth noting that the procedure of extracting of the
tidal variations used in the above papers needs accumulation of the
data for several weeks of observations
[ Burrage et al., 1995a].
It
is because the UARS was slowly precessing along longitude (
72o latitude band. During 24
hours the measurements cover all the longitudes. The results of
observations of the wind tidal variations by the HDRI were
presented by
Burrage et al. [1995a, b\link2]
and
Hays et al. [1993, 1994].
It is worth noting that the procedure of extracting of the
tidal variations used in the above papers needs accumulation of the
data for several weeks of observations
[ Burrage et al., 1995a].
It
is because the UARS was slowly precessing along longitude (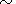 5o per day) and so 36 days of observations were needed to cover
all the LT moments
[ Hays et al., 1993].
5o per day) and so 36 days of observations were needed to cover
all the LT moments
[ Hays et al., 1993].
High horizontal resolution of the observations ( 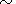 500 km) made
it possible to obtain such combinations of data, which provide
determination of the mode composition of the tides from an analysis
of the latitudinal structure of wind variations. The aim of this
paper is to develop the method of determination of the amplitudes
and phases of the migrating tidal modes from the latitudinal
distributions of the wind components obtained in UARS measurements.
We hope that such method of tidal mode parameter determination
would make it possible to determine the global characteristics of
the zonally averaged tidal variations for shorter observation
period than it has been done by
Burrage et al. [1995a, b\link2].
500 km) made
it possible to obtain such combinations of data, which provide
determination of the mode composition of the tides from an analysis
of the latitudinal structure of wind variations. The aim of this
paper is to develop the method of determination of the amplitudes
and phases of the migrating tidal modes from the latitudinal
distributions of the wind components obtained in UARS measurements.
We hope that such method of tidal mode parameter determination
would make it possible to determine the global characteristics of
the zonally averaged tidal variations for shorter observation
period than it has been done by
Burrage et al. [1995a, b\link2].
Processing of the Experimental Data
Results of the observations of the horizontal wind components in
the lower thermosphere on board the UARS satellite in February 1992
were presented by
Hays et al. [1992].
During this observational
period the satellite orbit parameters provided wind measurements in
the latitude band from 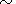 60o in the northern hemisphere to
60o in the northern hemisphere to 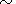 40o in the southern hemisphere. The experimental data were
presented as zonally averaged values of the wind horizontal
components at altitudes of 60-100 km at various LT moments.
40o in the southern hemisphere. The experimental data were
presented as zonally averaged values of the wind horizontal
components at altitudes of 60-100 km at various LT moments.
Let us assume that the diurnal variations of the wind in the lower
thermosphere are determined only by the tidal motions. The
expression for the wind horizontal components may be written as
U(r, q, t)=U0(r, q)+
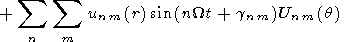 | (1) |
Here r and q are the height and colatitude, respectively; t is
the local time; n and m are the indices of the tidal modes; U is
the observed value of wind velocity; Unm are the tidal modes in
terms of which the wind velocity components are expanded; anm is
the amplitude of the tidal mode; gnm is the phase shift of
the tidal mode; U0 is the daily mean value of the wind velocity
component. Below writing the formulas we will omit the brackets
with arguments of the functions.
In the most cases it is sufficient to take into account the diurnal (n=1) and semidiurnal (n=2) tides at altitudes of the lower
thermosphere. The zonal averaging of the experimental data is taken
into account in (1), so the formulas do not contain any dependence
on longitude, and the indices of the tidal modes correspond to the
solar migrating tides, because the tidal modes with other relation
between the zonal wave numbers and frequencies disappear in the
averaging process. The Unm tidal modes, in terms of which the
horizontal wind components are expanded, are related to the Hough
functions by the relations of the classical tidal theory and satisfy
the orthogonality condition:
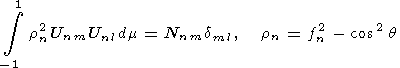 | (2) |
Here sn = nW is the frequency of the tidal perturbation; W is the angular velocity of the Earth's rotation; Nnm is a
normalizing factor; and dml is the Kroneker symbol.
Determination of the mode composition is reduced to determination
of the unknown amplitudes unm and phases gnm . Using (2)
one can obtain from (1)
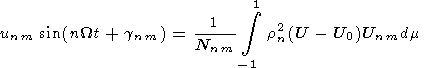 | (3) |
Knowing the velocity components at various moments one can obtain
from (3) a simple system of equations, solution of which determines
the unknown amplitudes and phases:
unm=Gnm2(t1)+Gnm2(t2)-2Gnm(t1)Gnm(t2)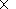
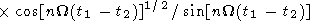 | (4) |
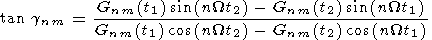 |
Here Gnm(t1) and Gnm(t2) are the values of the right-hand
sides of (3) for the t1 and t2 moments. The main uncertainties in
determination of the unknown amplitudes and phases of the tidal
modes are due to a limited latitudinal interval for which the
experimental data are available, and also to a character of the
latitude variations of the kernel in (3). For the considered period
of observations on board the UARS satellite there are no data for
latitudes above 60o in the northern hemisphere and 50o in the
southern hemisphere. The error in phase and amplitude determination
of the tidal modes due to a lack of measurements at high latitudes
is negligible for all semidiurnal solar migrating tides, because
the kernel in (3) rapidly decreases to the poles. Latitudinal
variations of the kernel in (3) for the diurnal tidal modes are of
a more complicated character and so the calculation errors for some
modes may be significant. Unlike the methods used to determine
the mode composition of the tides by the ground-based radar
observations, in the method suggested there is no requirement to
assume the set of Hough functions in advance to approximate the tidal
perturbations, and the inputs of various tidal modes into the
observed variations of the parameters are calculated directly by
(2)-(4).
Discussion
 The results of calculations of the amplitudes and local times of
the maximum of the geopotential semidiurnal tidal modes at
altitudes of 70-110 km are presented in Figure 1. The solid lines
show the tidal mode parameters, determined from the observations of
the wind meridional component, the dashed lines indicate the
parameters determined from the zonal component observations.
Unfortunately, a small volume of the experimental data presented by
Hays et al. [1992]
prevents determination of the daily mean wind
directly from the UARS observations. This can be helped if the
measurements for a long observational period or modern models of
the mean parameters of the upper atmosphere are used. The results
in Figure 1 were obtained without taking into account the daily
mean wind (U0 = 0) . Such calculations contain some uncertainty in
determination of the amplitudes and phases of the tidal modes and
this uncertainty may be significant if the zonal wind component is
used. The results obtained (bearing in mind a small volume of the
experimental data and neglecting by the mean wind) are of an
illustrative character and merely demonstrate capacities of the
method of tidal mode composition determination based on an analysis
of the wind distribution mode structure. The tidal perturbations of
the geopotential in Figure 1 were recalculated from the
corresponding perturbations of the wind components using the
relations of the classic tidal theory. Deviations from the
values obtained due to the errors in the satellite measurements of
the wind (
The results of calculations of the amplitudes and local times of
the maximum of the geopotential semidiurnal tidal modes at
altitudes of 70-110 km are presented in Figure 1. The solid lines
show the tidal mode parameters, determined from the observations of
the wind meridional component, the dashed lines indicate the
parameters determined from the zonal component observations.
Unfortunately, a small volume of the experimental data presented by
Hays et al. [1992]
prevents determination of the daily mean wind
directly from the UARS observations. This can be helped if the
measurements for a long observational period or modern models of
the mean parameters of the upper atmosphere are used. The results
in Figure 1 were obtained without taking into account the daily
mean wind (U0 = 0) . Such calculations contain some uncertainty in
determination of the amplitudes and phases of the tidal modes and
this uncertainty may be significant if the zonal wind component is
used. The results obtained (bearing in mind a small volume of the
experimental data and neglecting by the mean wind) are of an
illustrative character and merely demonstrate capacities of the
method of tidal mode composition determination based on an analysis
of the wind distribution mode structure. The tidal perturbations of
the geopotential in Figure 1 were recalculated from the
corresponding perturbations of the wind components using the
relations of the classic tidal theory. Deviations from the
values obtained due to the errors in the satellite measurements of
the wind (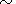 5 m s -1 ) do not exceed 200 m and about 2 h in
the determination of the amplitude of the geopotential perturbations and
the time of the tidal mode maximum, respectively. This estimate
apparently is strongly overestimated and obtained from (2)-(4) for
the case when the wind velocity does nor depend on latitude and is
equal to the measurement error. One can see that the parameters of
the tidal modes determined by different wind components differ
significantly, but at altitudes of about 90 km their amplitudes are
fairly close to each other (Figure 1a). The symmetric tidal modes, (2,2) and (2,4) , which tend to increase in amplitude above
100 km, prevail within the entire height interval. The asymmetric (2,3) mode, the amplitude of which at an altitude of about 90 km exceeds
the amplitudes of the symmetric tidal modes, contributes
considerably to the structure of the semidiurnal tide at 90-100 km.
The differences in times of maximum of the tidal modes (Figure 1b)
determined by different components of the wind velocity are
fairly strong, although the tendencies in vertical profile
variation above 90 km coincide. Circles in Figure 1 show the
parameters of the tidal modes obtained in theoretical and
experimental studies at an altitude of 97 km. The open circles show
the mode structure of the semidiurnal tide based on the
Forbes and Vial [1989]
results of numerical simulation for spring equinox. The
closed circles show parameters of the tidal modes obtained by
Forbes and Salah [1991]
in the radar measurements of the wind in
the course of the LTCS-1 Program in September 1987. Comparison of
these results to the mode structure determined by the UARS
measurements is in some sense verified by the fact that the
considered observational period is close to equinox. One can see in
Figure 1a that the amplitudes of the
geopotential perturbations obtained in this paper significantly exceed other results
[ Forbes and Salah, 1991].
5 m s -1 ) do not exceed 200 m and about 2 h in
the determination of the amplitude of the geopotential perturbations and
the time of the tidal mode maximum, respectively. This estimate
apparently is strongly overestimated and obtained from (2)-(4) for
the case when the wind velocity does nor depend on latitude and is
equal to the measurement error. One can see that the parameters of
the tidal modes determined by different wind components differ
significantly, but at altitudes of about 90 km their amplitudes are
fairly close to each other (Figure 1a). The symmetric tidal modes, (2,2) and (2,4) , which tend to increase in amplitude above
100 km, prevail within the entire height interval. The asymmetric (2,3) mode, the amplitude of which at an altitude of about 90 km exceeds
the amplitudes of the symmetric tidal modes, contributes
considerably to the structure of the semidiurnal tide at 90-100 km.
The differences in times of maximum of the tidal modes (Figure 1b)
determined by different components of the wind velocity are
fairly strong, although the tendencies in vertical profile
variation above 90 km coincide. Circles in Figure 1 show the
parameters of the tidal modes obtained in theoretical and
experimental studies at an altitude of 97 km. The open circles show
the mode structure of the semidiurnal tide based on the
Forbes and Vial [1989]
results of numerical simulation for spring equinox. The
closed circles show parameters of the tidal modes obtained by
Forbes and Salah [1991]
in the radar measurements of the wind in
the course of the LTCS-1 Program in September 1987. Comparison of
these results to the mode structure determined by the UARS
measurements is in some sense verified by the fact that the
considered observational period is close to equinox. One can see in
Figure 1a that the amplitudes of the
geopotential perturbations obtained in this paper significantly exceed other results
[ Forbes and Salah, 1991].
It is worth noting that a significant increase of the (2,3) mode in
comparison with the main symmetric modes, (2,2) and (2,4) , is found
in the radar observations of
Forbes and Salah [1991].
The same
relationship between the inputs of various tidal modes is typical for
our results. It can be seen in Figure 1b that at an altitude of about
97 km the phases of the tidal modes obtained in the radar
observations at autumn equinox agree well with the phases
determined by the measurements of the zonal wind component, and the
phases of the tidal modes measured by
Forbes and Vial [1989]
are
closer to the phases determined by the measurements of the
meridional wind component. Such a difference in the tidal mode phases can
not be explained by a single reason. It is widely known that the equinox
periods are characterized by a rapid change of the tidal phases
[ Manson et al., 1989],
therefore coincidences, as well as
differences, based on a comparison to a small amount of data may be
occasional. Moreover, the amplitudes and phases of the tidal modes
determined from the ground-based observations depend on the number
of stations used for the analysis, their geographic position and
the instrumentation used
[ Forbes and Salah, 1991].
Due to that, the
UARS wind observations have a considerable advantage in
determination of the tide mode composition as compared with
ground-based measurements. The amplitude and phase differences of
the semidiurnal solar migrated tides determined from the
measurements of the zonal and meridional wind components observed
on board the UARS are apparently due to the fact that in the
calculations performed no daily mean wind has been taken into
account. To evaluate influence of the mean flow on the semidiurnal
tide mode structure. a calculation has been performed using the
zonal component of the mean wind at altitudes of 70-80 km from the
CIRA-65 empirical model. The results are shown in Figure 1 by the
dashed line. Figure 1 demonstrates that taking into account of the
daily mean wind alters significantly parameters of the principal
tidal modes (2,2) and (2,3) and only slightly influence other tidal
modes.
 The mode structure obtained by satellite measurements was used to
reconstruct the semidiurnal tidal parameters at middle latitudes.
The amplitudes and phases of the tidal modes determined from
observations of the meridional and zonal components of the wind
velocity (Figure 1) were used to calculate the tides in these
components. Figure 2 shows the results of calculations for the
latitude of 50o and also the results of radar observations in
February. The measurements at various stations were presented by
Manson et al. [1989]
and are shown in Figure 2 in the following
way: closed circles - Garchy (47o N, 3o E), open
circles - Colm (52o N, 15o E), squares - Saskatoon (52o N,
107o W).
The mode structure obtained by satellite measurements was used to
reconstruct the semidiurnal tidal parameters at middle latitudes.
The amplitudes and phases of the tidal modes determined from
observations of the meridional and zonal components of the wind
velocity (Figure 1) were used to calculate the tides in these
components. Figure 2 shows the results of calculations for the
latitude of 50o and also the results of radar observations in
February. The measurements at various stations were presented by
Manson et al. [1989]
and are shown in Figure 2 in the following
way: closed circles - Garchy (47o N, 3o E), open
circles - Colm (52o N, 15o E), squares - Saskatoon (52o N,
107o W).
The tidal amplitudes based on the UARS measurements exceed those
observed, especially for the zonal velocity component below 90 km
(Figure 2b). Tidal amplitudes in the meridional velocity
component below 100 km agree with the Saskatoon data (Figure 2a).
The tide amplitudes in the horizontal wind components measured at
Colm are significantly lower the ones obtained by us. The time of
tide maximum derived from the observations of the velocity
meridional component (Figure 2a) differs significantly from the
observational data, whereas the calculated time of tidal maximum in
the zonal wind component agrees well with the observations at
altitudes of 80-100 km (Figure 2b).
The discrepancies in the parameters of the observed and calculated
tides may be due to the difference in methods used to determine the
wind in the lower thermosphere from satellite and radar data. It
should be noted that the UARS wind observations show that the wind
velocity measured by HRDI exceeds the velocities obtained by the
ground-based radar measurements
[ Burrage et al., 1996].
Evidently,
the question of determination of the wind in the lower thermosphere
by ion drifts measured in radar observations and by Doppler
measurements of the molecular oxygen spectra on board the UARS
satellite requires special consideration. Comparison of the
results obtained in this paper with the characteristics of the
semidiurnal tides derived from the HRDI measurements for two years
of UARS observations
[ Burrage et al., 1995b]
demonstrates a
satisfactory agreement for the amplitude of the wind meridional
component and the time of a tide maximum in the wind zonal
component. At 95 km, the amplitude of the velocity meridional
component and the moment of the maximum of the velocity zonal
component are 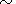 30 m s -1 and
30 m s -1 and 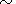 8 h,
respectively
[ Burrage et al., 1995b].
In our calculations we obtained these parameters to be
8 h,
respectively
[ Burrage et al., 1995b].
In our calculations we obtained these parameters to be 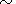 40 m s -1 and
40 m s -1 and 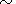 8 h.
The differences in the amplitude of the
velocity zonal component and the moment of the maximum are rather
strong. Apparently, the principal source of these differences is
the fact that we did not take into account the daily mean wind,
which influences the tide mode composition (see Figure 1). The
amplitudes and phases of the semidiurnal tidal modes obtained with
allowance for the daily mean zonal wind (dashed lines in Figure 1)
were used to calculate the semidiurnal tide in the zonal wind
component. The results are presented in Figure 2b by the dashed
line and demonstrate that use of the specifies mode composition of
the tides improves the agreement of the calculated and observed
tide parameters. Thus, calculating the tidal mode structure from
observations of the lower thermospheric wind, one should take into
account the input of the wind daily mean component. In the
calculation methods of the tide mode structure based on analysis of
the vertical profiles of the wind
[ Fakhrutdiniva and Ishmuratov, 1991;
Forbes and Salah, 1991]
obtained in radar observations, the input
of the daily mean wind should be taken into account directly in the
equations for the vertical structure of the modes.
8 h.
The differences in the amplitude of the
velocity zonal component and the moment of the maximum are rather
strong. Apparently, the principal source of these differences is
the fact that we did not take into account the daily mean wind,
which influences the tide mode composition (see Figure 1). The
amplitudes and phases of the semidiurnal tidal modes obtained with
allowance for the daily mean zonal wind (dashed lines in Figure 1)
were used to calculate the semidiurnal tide in the zonal wind
component. The results are presented in Figure 2b by the dashed
line and demonstrate that use of the specifies mode composition of
the tides improves the agreement of the calculated and observed
tide parameters. Thus, calculating the tidal mode structure from
observations of the lower thermospheric wind, one should take into
account the input of the wind daily mean component. In the
calculation methods of the tide mode structure based on analysis of
the vertical profiles of the wind
[ Fakhrutdiniva and Ishmuratov, 1991;
Forbes and Salah, 1991]
obtained in radar observations, the input
of the daily mean wind should be taken into account directly in the
equations for the vertical structure of the modes.
 Similar calculations are performed to determine parameters of the
diurnal tidal modes. It was assumed in calculations by (2)-(4)
that the solar diurnal tides are determined by inputs of the (1,1) , (1,-1 ), (1,-2 ), (1,4) , and (1,3) tidal modes. The calculations
performed demonstrate that the diurnal tide structure is mainly
determined by the (1,1) mode. Some input into the diurnal
variations below 90 km is also made by the (1,-1 ) and (1,-2 ) modes,
their amplitudes decreasing rapidly with height. It is worth noting
that the error of the method of mode input calculation for the (1,-1 ) and (1,-2 ) modes in the UARS observational period in
question is rather high (
Similar calculations are performed to determine parameters of the
diurnal tidal modes. It was assumed in calculations by (2)-(4)
that the solar diurnal tides are determined by inputs of the (1,1) , (1,-1 ), (1,-2 ), (1,4) , and (1,3) tidal modes. The calculations
performed demonstrate that the diurnal tide structure is mainly
determined by the (1,1) mode. Some input into the diurnal
variations below 90 km is also made by the (1,-1 ) and (1,-2 ) modes,
their amplitudes decreasing rapidly with height. It is worth noting
that the error of the method of mode input calculation for the (1,-1 ) and (1,-2 ) modes in the UARS observational period in
question is rather high ( 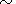 50%) and thus the result obtained is
merely of a qualitative nature. In the same way as for the
semidiurnal tides, differences in tidal mode amplitude and phase,
determined from different wind components, appear. Figure 3 shows
the amplitudes and the time of maximum of the diurnal tide in the
velocity horizontal components at an latitude of 50o calculated
by the tidal mode parameters determined from the satellite
measurements. The results of radar observations of the diurnal
tides for February by
Manson et al. [1989]
are also shown in Figure 3.
The indexing is the same as in Figure 2. It should be kept
in mind that the comparison of our results with the results
obtained earlier is of a qualitative character. Moreover, the tide
observations show significant interannual variation of the diurnal
tide amplitudes (see
Burrage et al. [1995b]).
It can be seen that
the amplitudes of the diurnal tide calculated in this paper exceed
significantly the observed values. A significant depletion of the
diurnal tide amplitude is seen above 90 km, which is due to the
dissipative processes in the thermosphere. The time of tidal maximum
determined for the meridional wind component differs significantly
from that observed (Figure 3a). However, the tidal phase
calculated for the wind zonal component agrees well with the
observations above 80 km (Figure 3b). Possible reasons of such
discrepancies between our results and observations were discussed above
while analyzing the semidiurnal tides.
50%) and thus the result obtained is
merely of a qualitative nature. In the same way as for the
semidiurnal tides, differences in tidal mode amplitude and phase,
determined from different wind components, appear. Figure 3 shows
the amplitudes and the time of maximum of the diurnal tide in the
velocity horizontal components at an latitude of 50o calculated
by the tidal mode parameters determined from the satellite
measurements. The results of radar observations of the diurnal
tides for February by
Manson et al. [1989]
are also shown in Figure 3.
The indexing is the same as in Figure 2. It should be kept
in mind that the comparison of our results with the results
obtained earlier is of a qualitative character. Moreover, the tide
observations show significant interannual variation of the diurnal
tide amplitudes (see
Burrage et al. [1995b]).
It can be seen that
the amplitudes of the diurnal tide calculated in this paper exceed
significantly the observed values. A significant depletion of the
diurnal tide amplitude is seen above 90 km, which is due to the
dissipative processes in the thermosphere. The time of tidal maximum
determined for the meridional wind component differs significantly
from that observed (Figure 3a). However, the tidal phase
calculated for the wind zonal component agrees well with the
observations above 80 km (Figure 3b). Possible reasons of such
discrepancies between our results and observations were discussed above
while analyzing the semidiurnal tides.
Conclusion
A new method to determine parameters of the solar diurnal and
semidiurnal tides in the mesosphere and lower thermosphere from
observations of the horizontal wind components on board the UARS
satellite is suggested.
The method is based on an assumption that the temporal variability
of the global distribution of parameters in this atmospheric region
is governed by propagation of the solar migrating tides. The UARS
measurements cover a wide latitudinal range and make it possible to
determine the mode structure of the solar tides in the atmosphere,
using the properties of orthogonal modes. Our method is a
development of the idea of studying the tidal structure from the
UARS observations applied to the diurnal tides by
Hays [1994].
The develop procedures of calculation of the tidal mode input and
diurnal and semidiurnal mode parameters are applied to a limited
set of the UARS observations in February 1991. The results of the
calculations lead to the following conclusions:
1. The amplitudes and phases of the tidal modes determined by
observations of the zonal and meridional components of the wind
differ. Parameters of the above modes depend significantly on the
daily mean wind. One of possible reasons of the difference in
parameters of the tidal modes determined by different wind
components may be related to not taking into account this factor in
the above described calculations.
2. The semidiurnal tide structure is mainly determined by the (2,2) and (2,4) modes. The calculations reveal a significant increase of
the mode (2,3) amplitude between 90 and 100 km. An increase of the
input of this mode during equinoxes was also detected in the radar
observations by
Forbes and Salah [1991].
The diurnal tide structure
is mainly determined by the (1,1) tidal mode.
3. Calculations of the midlatitude tidal parameters using the mode
structure determined by the measurements on board UARS satellite
show that the calculated tide amplitudes exceed the amplitudes
obtained in the radar observations, especially for the diurnal
tide. The times of tidal maxima in the meridional wind component
differ significantly from the observational results, whereas the
times of maxima of the diurnal and semidiurnal tides in the zonal
component of the wind agree well with the observational data.
The results of the preliminary study show that the UARS
measurements open broad possibilities to explore the tide
morphology in the mesosphere and lower thermosphere.
The UARS measurements provide a possibility to improve
significantly the accuracy of determination of the tidal mode
structure, which is very important for theoretical modeling of the
upper atmosphere. Attracting to tide analysis observations of other
atmospheric parameters on board UARS (for example, the temperature)
would improve tidal parameter determination and eliminate the
uncertainties arising when the wind measurements are used.
Acknowledgments
This work was supported by the Russian Foundation
for Basic Research (project 94-05-17433).
References
Burrage, M. D., et al., Long-term variability in the solar diurnal
tide observed by HRDI and simulated by the GSWM,
Geophys. Res. Lett., 22, 2641, 1995a.
Burrage, M. D., et al., Latitude and seasonal dependence of the
semidiurnal tide observed by HRDI,
J. Geophys. Res., 100, 11,313,
1995b.
Burrage, M. D., et al., Validation of the mesosphere and lower
thermosphere winds from the High Resolution Doppler Imager on UARS,
J. Geophys. Res., 101, 10,365, 1996.
CIRA 1965, COSPAR Working Group IY, Amsterdam, 1965.
Fakhrutdinova, A. Ya., and R. A. Ishmuratov, Seasonal variations of
the mode input into the semidiurnal tidal motions in the
midlatitude lower thermosphere,
Geomagn. Aeron., 31 (5), 904, 1991.
Forbes, J. M., and J. E. Salah, Mesosphere-thermosphere tidal
coupling during the September 21-25, 1987, LTCS-1 campaign,
J. Geophys. Res., 96 (A2), 1135, 1991.
Forbes, J. M., and F. Vial, Monthly simulations of the solar
semidiurnal tide in the mesosphere and lower thermosphere,
J. Atmos. Terr. Phys., 51, 649, 1989.
Forbes, J. M., R. G. Roble, and C. G. Fesen, Acceleration, heating
and composition mixing of the thermosphere due to upward
propagating tides, J. Geophys. Res., 98 (A1), 311, 1993.
Hays, P. B., et al., Remote sensing of mesosphere winds with the
High Resolution Doppler Imager, Planet. Space Sci., 40 (12), 1599,
1992.
Hays, P. B., et al., The High Resolution Doppler Imager on the
Upper Atmosphere Research Satellite,
J. Geophys. Res., 98, 10,713,
1993.
Hays, P. B., et al., Observations of the diurnal tide from space,
J. Atmos. Sci., 51, 3077, 1994.
Manson, A. H., et al., Climatologies of semidiurnal and diurnal
tides in the middle atmosphere (70-110 km) at middle latitudes
(40-55o),
J. Atmos. Terr. Phys., 51 (7/8), 579, 1989.
Load file for printing and local use.
This document was generated by TeXWeb (Win32, v.1.0) on March 25, 1998.
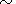 50-115 km in the daytime and
50-115 km in the daytime and 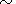 90 km at
night. The detailed description of the HRDI and of its functioning
on board UARS was given by
Hays et al. [1993].
The orbit parameters
provide measurements in the
90 km at
night. The detailed description of the HRDI and of its functioning
on board UARS was given by
Hays et al. [1993].
The orbit parameters
provide measurements in the 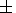 72o latitude band. During 24
hours the measurements cover all the longitudes. The results of
observations of the wind tidal variations by the HDRI were
presented by
Burrage et al. [1995a, b\link
72o latitude band. During 24
hours the measurements cover all the longitudes. The results of
observations of the wind tidal variations by the HDRI were
presented by
Burrage et al. [1995a, b\link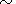 5o per day) and so 36 days of observations were needed to cover
all the LT moments
[ Hays et al., 1993].
5o per day) and so 36 days of observations were needed to cover
all the LT moments
[ Hays et al., 1993].